Магнитостатическое поле в вакууме. Часть 1

1.

Тема 1. МАГНИТОСТАТИЧЕСКОЕ
ПОЛЕ В ВАКУУМЕ. Часть 1
Опыты:
1. Вокруг проводников с
электрическим током
существует магнитное поле
(опыты Эрстеда, 1820).

2.

2.На движущий заряд в
магнитном поле действует сила
Лоренца
FЛ q[ B]
FЛ q B sin
Если
Силовой характеристикой магнитного поля в данной точке
является вектор магнитной индукции
.
Он численно равен силе, действующей со стороны поля на
единичный заряд, движущийся с единичной скоростью в
направлении, перпендикулярном линиям поля.
Аналогом
в электрическом поле является вектор
- силовая характеристика этого поля .

3.

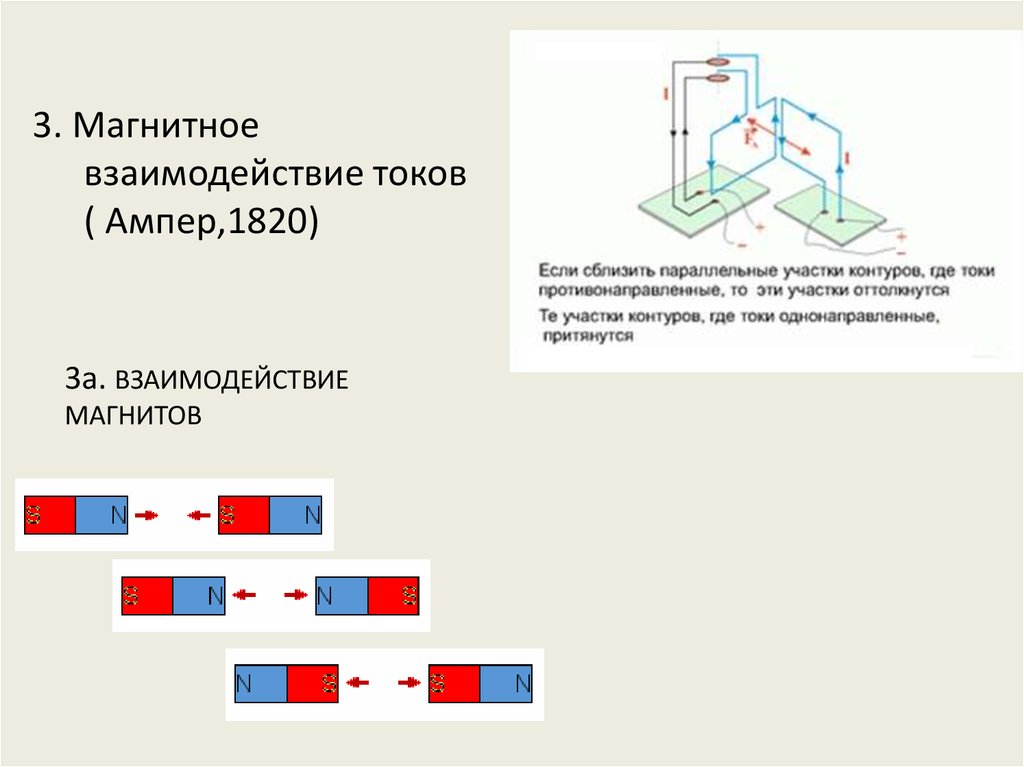
3. Магнитное
взаимодействие токов
( Ампер,1820)
3a. ВЗАИМОДЕЙСТВИЕ
МАГНИТОВ

4.

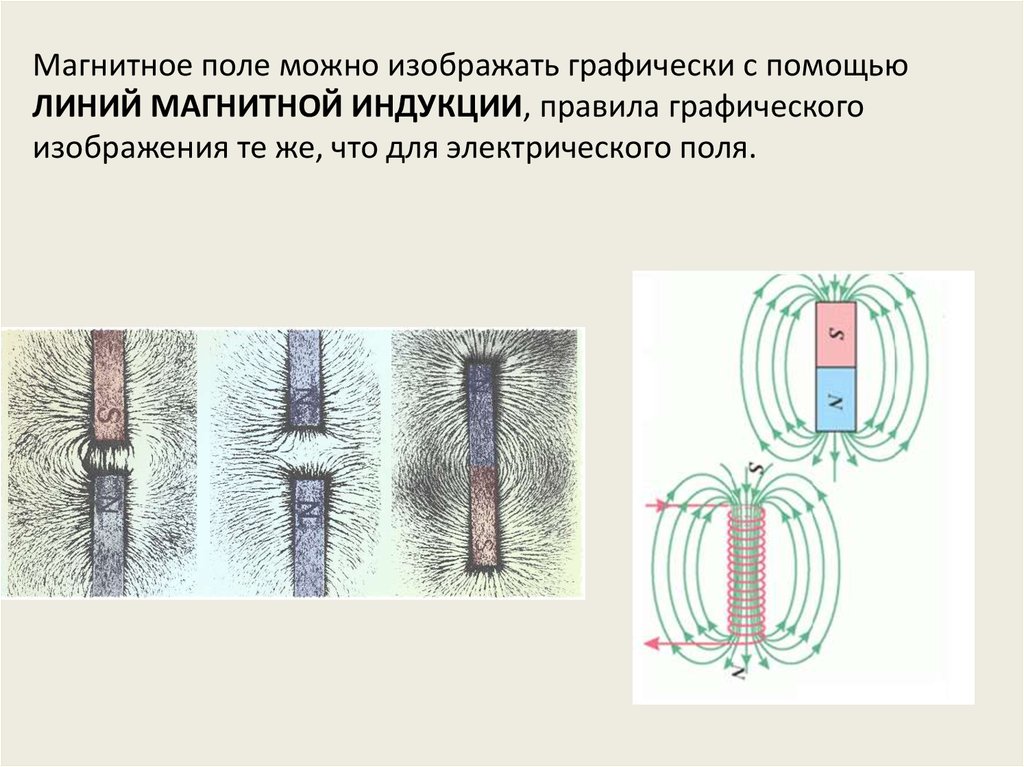
Магнитное поле можно изображать графически с помощью
ЛИНИЙ МАГНИТНОЙ ИНДУКЦИИ, правила графического
изображения те же, что для электрического поля.

5. 1. ПОЛЕ ДВИЖУЩЕГОСЯ ЗАРЯДА

Из опыта: магнитное поле может создаваться движущимися зарядами.
Из опыта : заряд создает в т. А поле,
мгновенное значение магнитной индукции
которого
0 q v
, r
B
4 r 3
(2.1)
0 4 10 Гн / м;
7
Исследуем (2.1):
1.
При v=0,B=0. В той системе отсчета, где заряд покоится, его
магнитное поле исчезает. Т.к. механическое движение относительно,
то существование магнитного поля относительно и
зависит от выбора системы отсчета.

6.

0 q v
, r
B
4 r 3
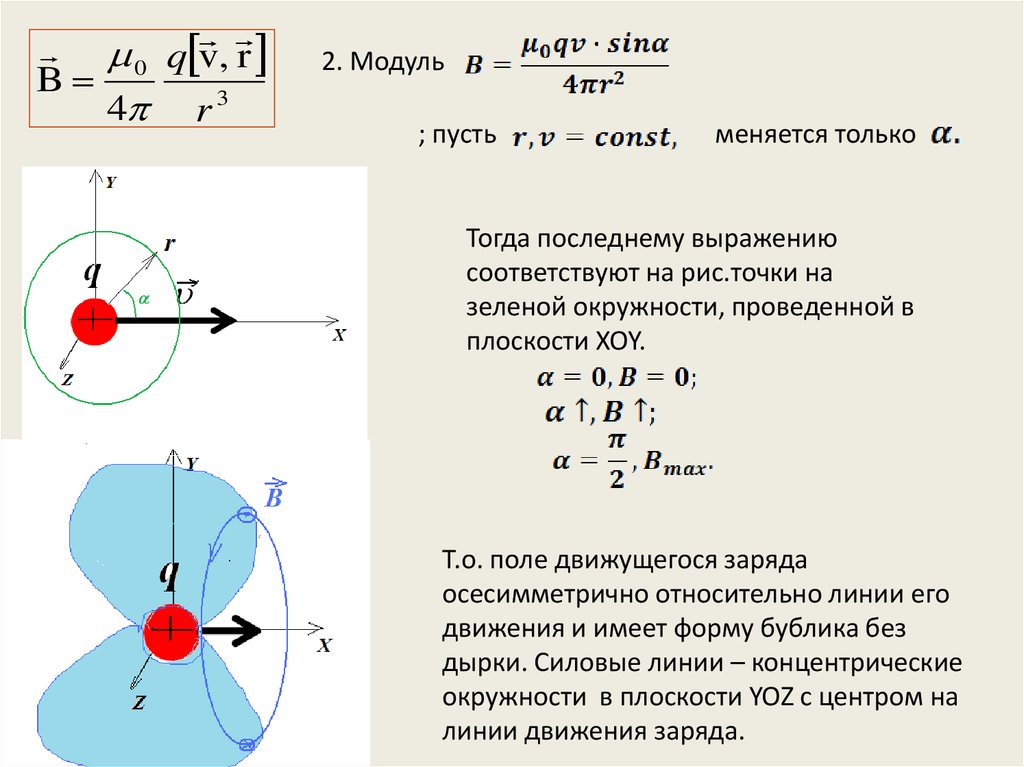
2. Модуль
; пусть
меняется только
Тогда последнему выражению
соответствуют на рис.точки на
зеленой окружности, проведенной в
плоскости XOY.
Т.о. поле движущегося заряда
осесимметрично относительно линии его
движения и имеет форму бублика без
дырки. Силовые линии – концентрические
окружности в плоскости YOZ с центром на
линии движения заряда.

7. На практике для создания стационарных магнитных полей используют проводники с током. Упорядоченно движущиеся заряды ,

составляющие ток,
создают совокупное магнитное поле.
Т.о. источниками магнитного поля являются движущиеся заряды
и токи.
Из опыта известен ПРИНЦИП СУПЕРПОЗИЦИИ ДЛЯ ИНДУКЦИИ
МАГНИТНЫХ ПОЛЕЙ:
Индукция магнитного поля, созданного в данной точке несколькими
источниками, есть векторная сумма индукций полей, созданных в
этой точке каждым источником в отдельности.

8. 2. ЗАКОН БИО-САВАРА-ЛАПЛАСА

Закон Био-Савара-Лапласа определяет индукцию магнитного поля,
созданного бесконечно малым участком проводника с током.
Найдем магнитную индукцию
поля, созданного в произвольной т.А
элементом проводника с током
(направление
совпадает с
направлением тока I ) .
Векторы
отдельных
электронов в т.А
направлены
одинаково.
0 q v
, r
B
4 r 3
Рис.12.5

9.

Этот слайд – факультатив!
u
dN nSd ,
скорость теплового движения,
скорость упорядоченного
движения отдельного носителя заряда
0
u u u
0 q0 [ u r ]
dB dN Bi
nSd
3
4
r
j q0 n u
I jS
0 j dl r S
0 jdl r S 0 Idl r 0 I dl r
dB
4
4
4 r 3
4 r 3
r3
r3

10.

Элемент проводника
с током I создает в точке А
индукцию поля
0 I dl , r
dB
3
4
r
(1)
r -радиус-вектор, проведенный
из элемента dl проводника
в точку А.
(1)- закон Био-Савара-Лапласа.
Рис.12.5
Модуль индукции поля:
Индукция поля, созданного в т.А проводником конечной длины:
Рассмотрим примеры применения закона Био-Савара-Лапласа к расчету
магнитных полей токов простой конфигурации.

11.

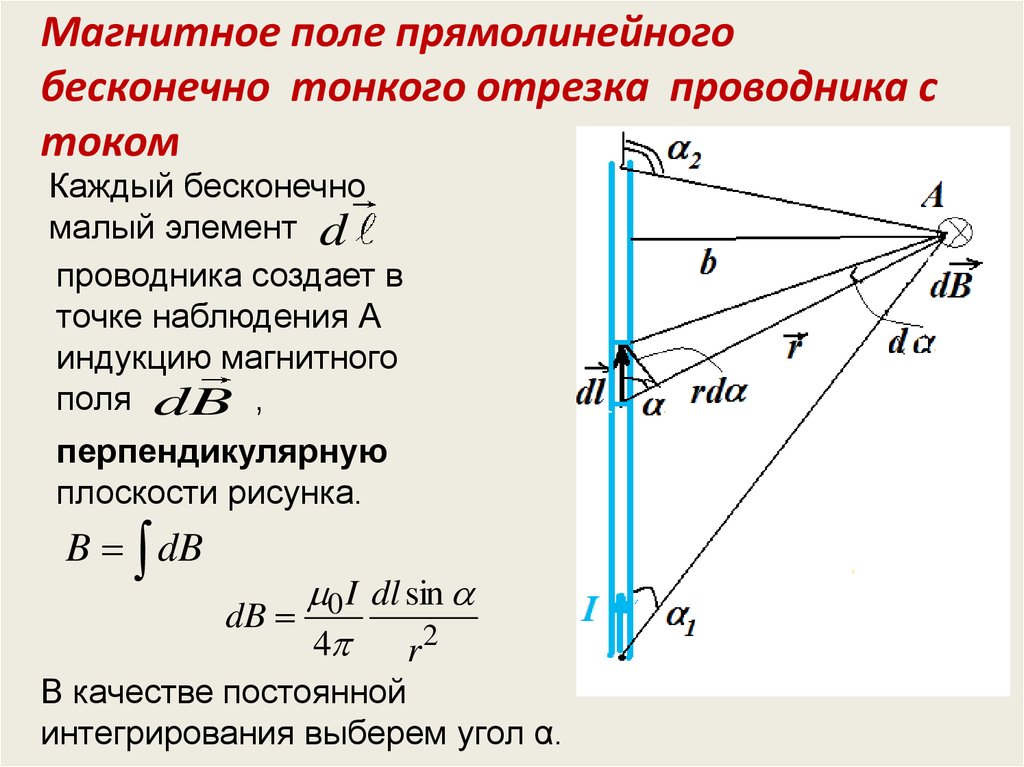
Магнитное поле прямолинейного
бесконечно тонкого отрезка проводника с
током
Каждый бесконечно
малый элемент d
проводника создает в
точке наблюдения А
индукцию магнитного
поля dB ,
перпендикулярную
плоскости рисунка.
B dB
0 I dl sin
dB
4
r2
В качестве постоянной
интегрирования выберем угол α.

12.

0 I dl sin
dB
4
r2
- индукция поля, созданного отрезком прямолинейного
проводника с постоянным током

13.

Для бесконечного
проводника с током
0 I
B
(cos 0 cos )
4 b
0 I
0 I
2
4 b
2 b

14.

Направление линий магнитной индукции задается правилом
правого винта:
головка винта, ввинчиваемого по направлению тока,
вращается в направлении линий магнитной индукции.

15.

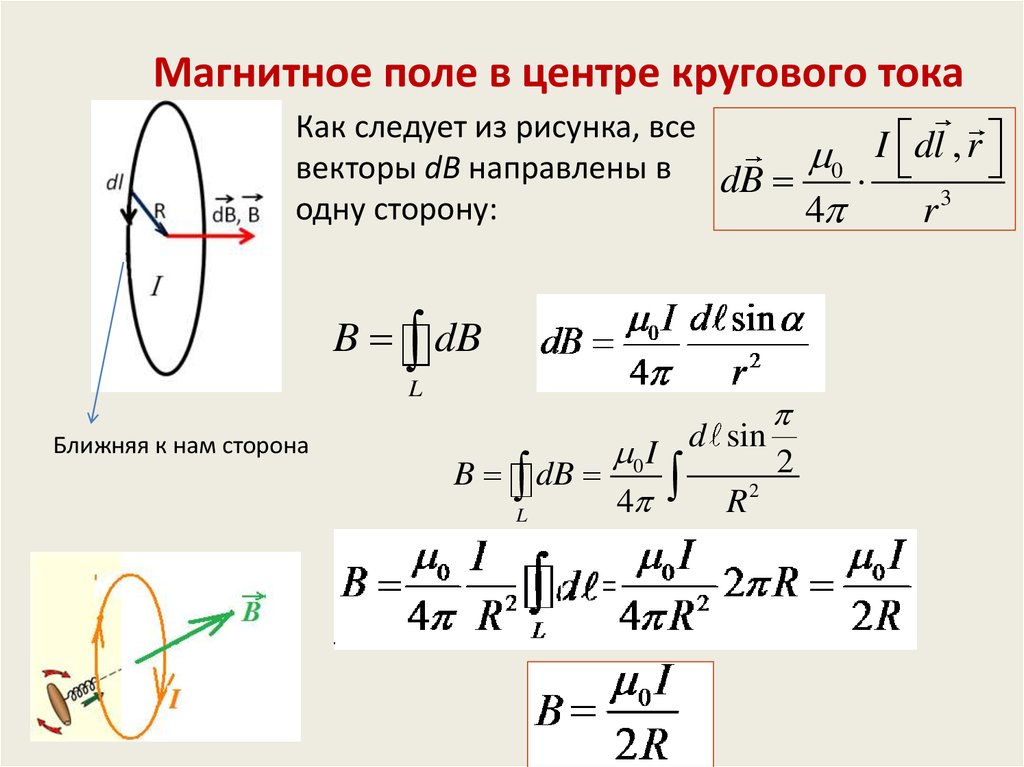
Магнитное поле в центре кругового тока
Как следует из рисунка, все
I dl , r
векторы dB направлены в dB 0
одну сторону:
4
r3
B
dB
L
Ближняя к нам сторона
0 I d sin 2
B dB
2
4
R
L

16.

Магнитное поле на оси кругового тока
Ближняя к нам сторона

17.

Магнитное поле на оси кругового тока
0 Id sin
dB
4
r2
/ 2 (sin 1),
B
L
cos
R
r
r R2 x2
0 Id
0 I cos
cos
2 R.
2
2
4 r
4 r

18.

Линии магнитной индукции поля кругового витка с током