Метод наложения. Электрические цепи постоянного тока

1. Метод наложения

U1(t)
U2(t)
Метод наложения
Электрические цепи постоянного тока
Кафедра
ТОЭ НГТУ

2.

U2(t)
U1(t)
Метод наложения
Для доказательства воспользуемся методом контурных токов
k1
k 2
km
Ik E11
E22
Emm
(1)
Если расписать контурные ЭДС как алгебраическую сумму ЭДС,
действующих в замкнутом контуре, то получим
Ik E1gk1 E2gk 2 E3gk 3 Emgkm
(2)
Каждое слагаемое во (2) есть частичный ток, обусловленной
каждой из ЭДС в отдельности
I k E1 g k 1
I k E2g k 2
Ik
E2g k 3
Тогда (2) приобретает вид
I k I k I k I
Электрические цепи постоянного тока
(3)
Кафедра
ТОЭ НГТУ

3.

Метод наложения
E1 0.E 2 E 3 Em 0 I k
E 2 0.E1 E 3 Em 0 I k
Em 0.E1 E 2 Em 1 0 I k
m
Порядок расчета цепи методом наложения
1.Расставляем
токов в ветвях
положительные
направления
истинных
2.Поочередно оставляем в цепи по одной ЭДС. Остальные
ЭДС при этом равны нулю, но их внутренние сопротивления
оставлены.
3.Находим частичные токи в ветвях цепи от каждой ЭДС в
отдельности.
Линейные электрические цепи постоянного тока

4.

Метод наложения
4.Истинные токи в ветвях находятся как
алгебраическая сумма частичных токов.(Частичные
токи, совпадающие по направлению с истинным током,
берутся со знаком плюс, не совпадающие – со знаком
минус)
Некоторые свойства электрических цепей
1.Свойство взаимности
В некоторой электрической цепи ток Ik в ветви к, вызванный
ЭДС Еm в ветви m, равен току Im в ветви в ветви m,
вызванному ЭДС Еk ветви к, при условии Еk=Em .

5.

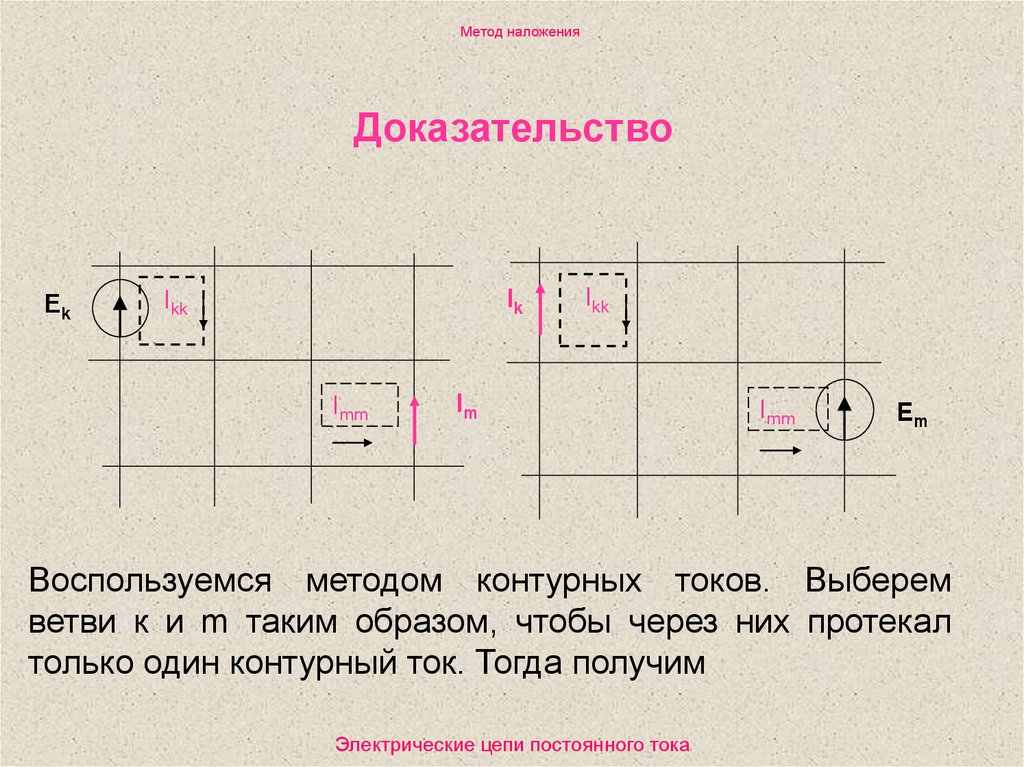
Метод наложения
Доказательство
Ek
Ik
Ikk
Imm
Ikk
Im
Imm
Em
Воспользуемся методом контурных токов. Выберем
ветви к и m таким образом, чтобы через них протекал
только один контурный ток. Тогда получим
Электрические цепи постоянного тока

6.

Некоторые свойства электрических цепей
k1
k 2
km
I k Ikk E11
E22
Emm
Im Imm E11 m1 E22 m2 Emm mm
(1)
(2)
Оставим в электрической цепи только по одной ЭДС.
Тогда выражения (1) и (2) приобретут вид
km
I k Em
mk
I m Ek
(3)
(4)
Но так как Ек = Еm, а Δmk = Δkm , то Im=Ik
Электрические цепи постоянного тока

7.

2. Линейные соотношения в линейных электрических
цепях
Если в линейной электрической цепи изменяется
некоторая ЭДС Еm, то токи в электрической цепи связаны с
этой ЭДС соотношениями I = А+ В Еm , где А и В некоторые
постоянные.
Доказательство
Воспользуемся методом контурных токов
I k E1g k 1 E 2g k 2 Em g km
(1)
В
А
I k A BE m
(2)
Id E1gd1 E2gd2 Emgdm
(3)
В1
А1
Электрические цепи постоянного тока

8.

Некоторые свойства электрических цепей
I k A BE m
(4)
Id A1 B1Em
(5)
Выразим из
4го Еm
Em
Ik A
B
Подставим Еm в (5)
Ik A
A
B1
Id A1 B1
A1
B1
Ik
B
B
B
С
Id Ñ DIk
D
(6)
Из 4,5,6 следует, что не только ЭДС и токи связаны
линейными соотношениями, но и токи в различных ветвях, а
также напряжения на элементах электрической цепи ,т.е.
U k C1 D1U m
Электрические цепи постоянного тока