Определение логарифма числа

1. Определение логарифма числа

Первые свойства
логарифмов
Учитель математики Попкова Т.Г.
г.Горячий Ключ МОУ СОШ №2

2.

Цели урока:
Разобрать понятие
логарифма числа
и его простейшие свойства.

3.

Невозможно изучить
новое без повторения
уже изученного.

4.

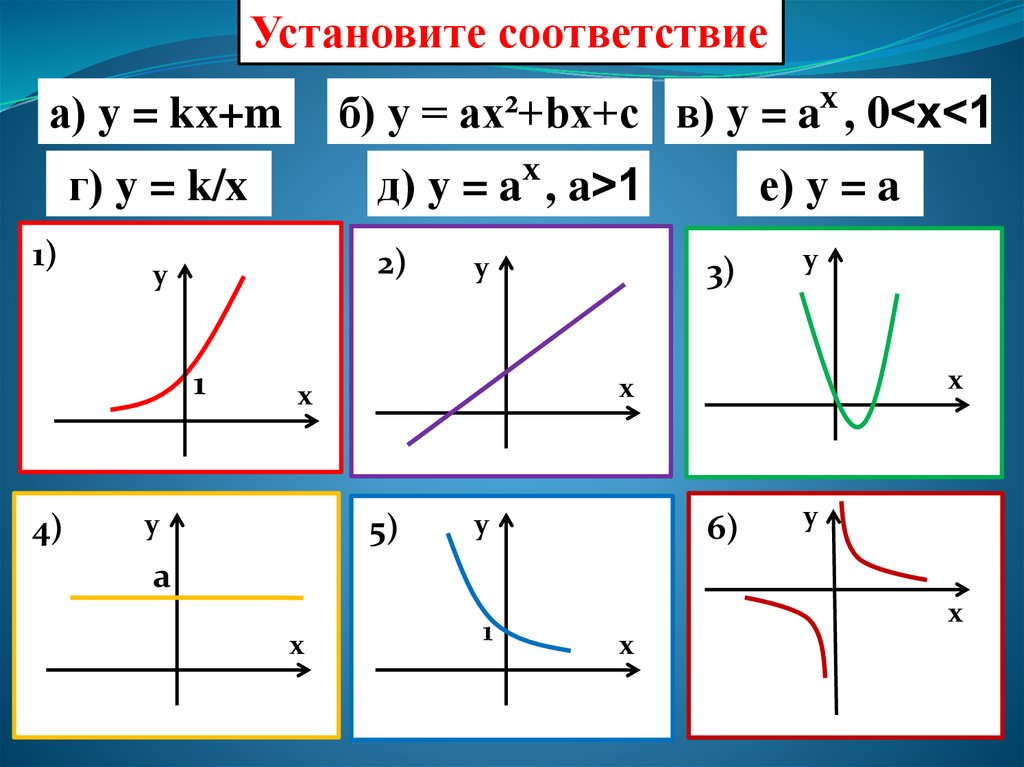
Установите соответствие
б) y = ax²+bx+c в) y = ax , 0<x<1
а) y = kx+m
x
г) y = k/x
1)
2)
у
1
4)
д) y = a , a>1
у
3)
у
х
х
х
у
е) y = a
5)
у
6)
у
a
х
1
х
х

5.

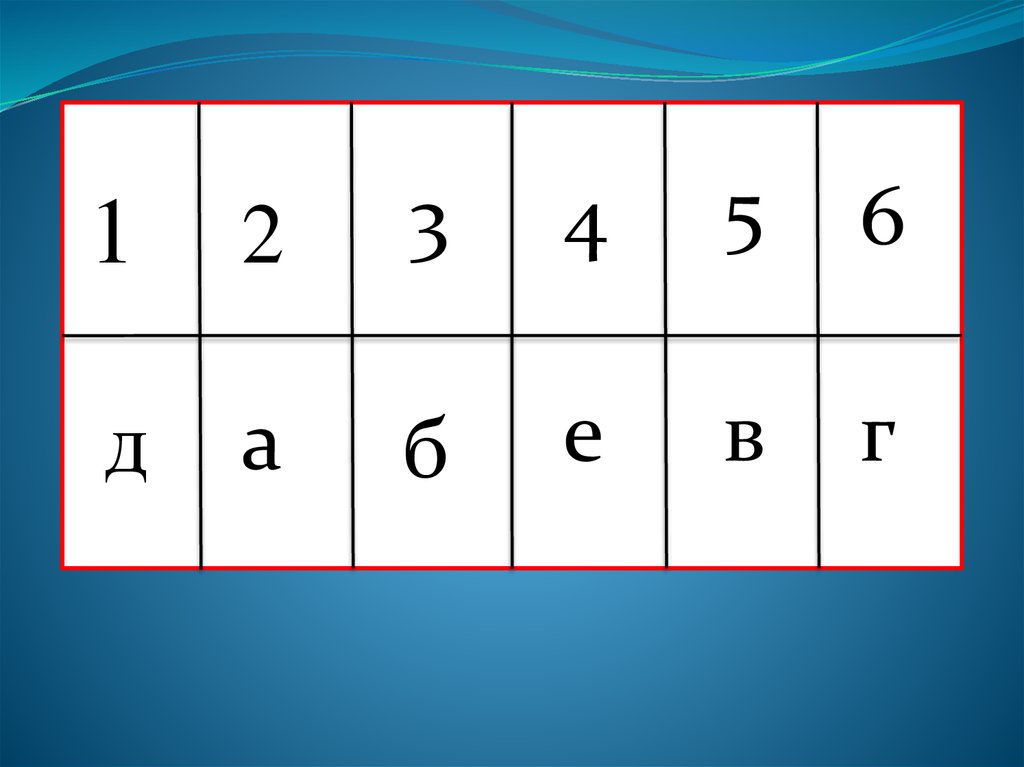
1
2
3
д
а
б
4
5
6
е
в
г

6.

Решить уравнения:
x
Проверка:
1) 3 = 27
1) x = 3
2) 3x + 2 = 0
2) x = -2/3
3) 3 + 9 = 0
3) Корней нет
4) x⁵ = 5
4)
5) x² - 4 = 0
5) x₁‚₂= ±2
x
x
6) 3 = 6
6) ?

7.

x
Рассмотрим подробнее уравнение 3 = 6.
Для исследования его возможных корней,
воспользуемся графическим способом.
y = 3 x экспонента
y
y = 6 горизонтальная
прямая
6
Получили
один корень
Ответ: ?
1
1
x₁
x

8.

Решая последнее уравнение,
мы столкнулись с проблемой
записи полученного ответа.
Прежних знаний для этого
явно недостаточно.
Можно оценить корень
1< x₁ < 2, т.к.
x
3 < 3 < 9.

9.

Выводы:
• уравнение имеет один корень
• корень – число
(показатель степени числа 3).
Такой вывод можно сделать для
любого уравнения вида
,
где
,
.

10.

Для корней показательных уравнений
используют запись
,
где
- логарифм числа b
по основанию .
Примеры:
x
1)12 = 5
x
2) 4 = 9
x
3) 0,7 = 0,49
, x = log₁₂ 5
, x = log₄9
, x = log₀‚₇0,49
x=2

11.

Мы получили новую математическую
модель – логарифм числа.
Логарифмом числа
по основанию
называется такой показатель степени k,
в который надо возвести , чтобы
получить , т.е.
log b = k,
.
Примеры: log₂16 = 4, т.к. 2⁴ = 16.
log₀‚₃0,09 =2, т.к. 0,3²=0,09

12.

Примеры:
1) log₂ 4 =
2 натуральное
2) log₂ 1/2 = -1 целое
3) log₂
4) log₂ 9 =
= 0,5 рациональное
Иррациональное число
Вывод: значение логарифма–
действительное число.

13.

Рассмотрим некоторые
свойства логарифма
1) loga a = 1
2) loga1= 0
3) если loga b = k и a k = b,
k
тогда log a a = k.
4) a
loga k
= k основное логарифмическое
тождество

14.

Далее:
1.Обучающая самостоятельная работа
по карточкам (приложение).
2.Работа по задачнику:
п.41, № 3-9 (а, б); 11-17(а, б)
3.Домашнее задание:
п.41, № 3-9 (в, г); 11-15(в)