Похожие презентации:
Определение логарифма
1. 1. Определение логарифма
Рассмотрим показательное уравнениеа х b, где а 0 и а 1, x R.
При b 0 это уравнение не имеет решений;
при b 0 показательное уравнение имеет
единственный
корень.
Этот
корень
называют логарифмом b по основанию а и
обозначают log a b .
2. Определение.
Логарифмом положительного числа bпо основанию а, где а 0 , a 1,
называется показатель степени, в
которую надо возвести основание а,
чтобы получить число b, т.е.
а b; x log a b , a
х
log a b
b
3.
Формулу a loga b b(где b 0, а 0, а 1 ) называют
основным логарифмическим тождеством.
4. Примеры. Заполнить пропуски:
1.log 2 8 ..., т.к. 2 8, а 2, b 8
2.
1
log 3 ...,
9
log 7 7 ...,
3.
...
1
1
т.к. 3 , а 3, b
9
9
т.к. 7... 7, а 7, b 7
...
4.
log 4 1 ..., т.к. 4 1, а 4, b 1;
5.
log ... 16 4, т.к. ... 16;
6.
1
1
5
log ...
5, т.к. ...
;
32
32
...
4
5. Примеры. Заполнить пропуски:
Примеры.7.
8.
9.
10.
...;
log4 5
4
1
2
log 1 3
log ... 4
5
2
...;
4
log1 3 ...
13
Заполнить пропуски:
3
.
4
6. Примеры.
11. Вычислить log 64 128 ?log 64 128 х,
по определению : 64 х 128
26 х 27
6х 7
7
x
6
7
Ответ : log 64 128 .
6
7. Примеры.
2 log3 512. 3
log3 5 2
3
5
13. Решить уравнение
log 3 1 х 2
3 1 х
2
х 8
2
1 25;
8. 2. Свойства логарифмов
При работе с логарифмамиприменяются следующие их свойства,
вытекающие из свойств показательной
функции:
При любом а 0 а 1 и любых
положительных чисел х и у выполнены
равенства:
9. Свойства логарифмов:
1.log a 1 0, т.к. а 1
2.
log a а 1, т.к. а а
0
1
3.
логарифм произведения равен сумме логарифмов:
4.
логарифм частного равен разности логарифмов:
log a ху log a х log a у
х
log a log a х log a у
у
5.
логарифм степени равен произведению
показателя степени на логарифм основания этой степени:
log a х р р log a х, где р R
10.
Основные свойства логарифмовшироко применяются в ходе
преобразований выражений,
содержащих логарифмы. При этом
используются формулы перехода от
одного основания логарифма к
другому основанию:
11.
log c b, где b 0, a 0, a 1, c 1, c 0.
1. log a b
log c a
1
2. log a b
log b a
3. log1 a b log a b
1
4. log a p b log a b,
p
.
a 0, a 1, b 0, p 0.
12. Примеры:
14. log 12 2 log 12 7215
15. log 2 15 log 2
16
5
log
16.
13 169
17. log 8 12 log 8 15 log 8 20
18.
log 3 8
log 3 16
13. Примеры:
14. log12 2 log12 72 log12 2 72 log12 144 215
15
log 2
log 2 16 4
15. log 2 15 log 2
16
15 16
16. log13
17.log
5
1
5
2
5
2
2
169 log13 169 log13 13 log13 13
5
5
8 x 16
4
12 20
3x
4
log 8 16 2 2
8 12 log 8 15 log 8 20 log 8
3
15
x 4 3
3
log
8
log
2
3 log 3 2 3
18.
3
3
4
log 3 16 log 3 2
4 log 3 2 4
14. 3. Логарифмирование и потенцирование
Действие нахождения логарифма числаназывают логарифмированием.
Нахождение положительного числа по его
логарифму называют потенцированием.
15. Примеры.
19. Прологарифмировать выражения:а) х 2а b; б) х
3
ab
3
;
в)
х
а
b
3
c
Ответ. а) log х log 2 3 log а log b;
1
б) log х log a log b 3 log c ;
2
1
1
в) log х log a log b.
2
6
16.
20. Пропотенцировать выражения:1
1
а) log х log a log b;
3
2
1
3
2
б) log х log a log b log с.
4
4
3
Ответ.
а) х
3
а
; б) х
b
4
3
ab
c
3
2
.
17. 4. Десятичные и натуральные логарифмы.
Десятичным логарифмом числаназывают логарифм этого числа по
основанию 10 и пишут:
log 10 b lg b
Натуральным логарифмом числа
называют логарифм этого числа по
основанию е, где e 2,7182818... 2,7
– иррациональное число, и пишут:
log e b ln b
18. Вычислите самостоятельно:
à) log 2 16 ...;á) log 2 64 ...;
â) log 2 2 ...;
ã) log 2 1 ...;
1
ä) log 2 ...;
2
log3 18
æ) 3
...;
1
å) log 2 ....;
8
5 log3 2
ç) 3
....
19. Упростить выражения, пользуясь основным логарифмическим тождеством:
1à)
2
6 log 1 2
á) 0,3
â) 7
ã) 8
2
2 log0 , 3 6
1
log7 9
2
log2 5
ä) 9 log3 12
å) 16
log4 7
æ) 0,125
log0 , 5 7
20. Упростить выражения, пользуясь основным логарифмическим тождеством:
1à)
2
6 log1 2
2
1
2
log1 2
2
6
26 64;
21. Упростить выражения, пользуясь основным логарифмическим тождеством:
1à)
2
6 log 1 2
á) 0,3
2
1
2
2 log0 , 3 6
log 1 2
2
6
26 64;
log0 , 3 6 2
0,3
6 2 36;
22. Упростить выражения, пользуясь основным логарифмическим тождеством:
1à)
2
6 log 1 2
á) 0,3
â) 7
2
1
2
2 log0 , 3 6
1
log7 9
2
log 1 2
26 64;
log0 , 3 6 2
0,3
7
2
6
1
log7 9 2
1
2
6 2 36;
9 3;
23. Найти число х по определению логарифма:
log 6 x 3 log 2 5 x 36 x
2 5 x
x 216
x 3
3
3
log 1 0,5 x 1
6
1
1
0,5 x
6
6 0,5 x
x 5,5










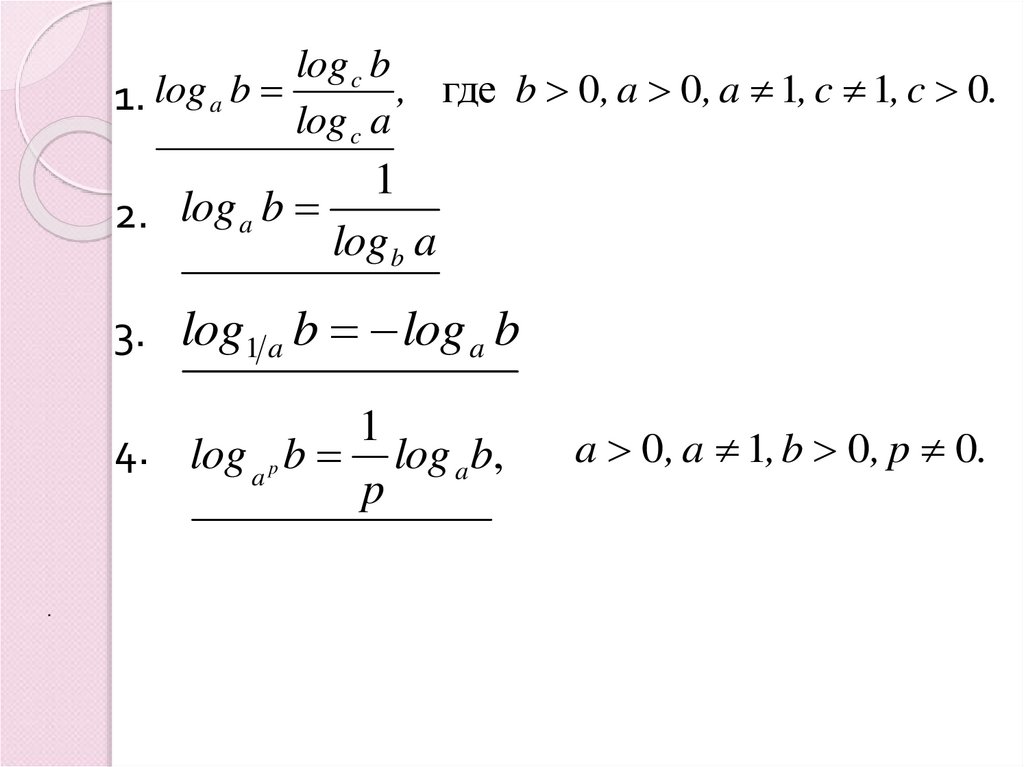












 Математика
Математика








