Поверхностный эффект в проводниках. (VI)

1.

VI. Поверхностный эффект в проводниках

2.

п
Рассмотрим границу раздела диэлектрик-проводник.
Для II-й среды:
I
k1
k2
пр
x
E0
6.1 .
0, т.е.
от величины
поле во II-й среде распространяется
по нормали к границе:
E2 E0 exp ik2 x E0 exp i ( i ) x .
Здесь
1
В соответствии с граничными
условиями Леонтовича, независимо
z
II
6.2
амплитуда поля при x=0.
Как известно, при условии (6.1):
a
2
1
6.3 ,
где - глубина проникновения.
*

3.

Тогда (6.2):
E2 E0 exp i 1 i x .
Плотность тока во II-й среде:
6.4
E E0 exp i i 1 x . 6.5
Поскольку поле и ток во II-й среде быстро убывают при увеличении х,
можно ввести поверхностную плотность тока:
0
0
S dx E0 exp i 1 i x dx
E0
E0 . 6.6
exp i i 1 x |
1 i 1 i
i i 1
E0
0
Сравнив (6.6) с законом Ома в дифференциальной форме (6.5) можно
записать (6.6) в виде закона Ома для поверхностной плотности тока:
S
E0 GS E0,
1 i
где
GS
6.7
удельная поверхностная проводимость.
1 i
*

4.

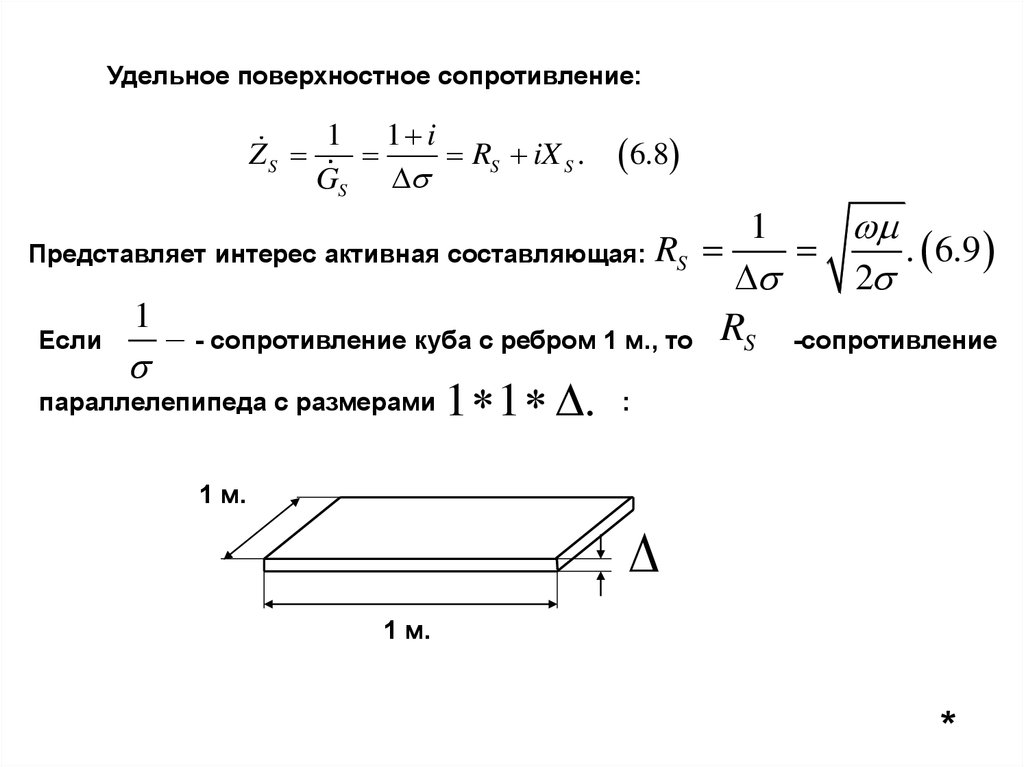
Удельное поверхностное сопротивление:
1 1 i
ZS
RS iX S .
GS
6.8
1
. 6.9
Представляет интерес активная составляющая: RS
2
1
Если
- сопротивление куба с ребром 1 м., то RS -сопротивление
параллелепипеда с размерами
1 1 .
:
1 м.
1 м.
*

5.

Поверхностный эффект возникает за счёт того, что проникшее в проводник
электромагнитное поле наводит в нём токи. Векторы E и H созданные
этими токами направлены в строну, противоположную векторам
E и
H «первичного» поля и ослабляют его.
В результате при протекании переменного тока по цилиндрическому
проводнику объёмная плотность тока в поперечном сечении проводника
максимальна у его поверхности и минимальна на оси.
Сильно выраженный поверхностный эффект имеет место, когда глубина
проникновения значительно меньше поперечного размера проводника.
В этом случае сопротивление проводника радиуса a можно рассчитывать
a радиусом a
как сопротивление на постоянном токе трубки с внешним
и толщиной стенки :
l
R
. 6.10
2 a
На постоянном токе:
a
Тогда
l
R
.
2
a
R
a
f a .
R 2
6.11
*

6.

Пример:
Тогда:
a 2 10
3
См
м., f 3 10 Гц, 6 10
(серебро).
м
8
7
R
250.
R
Как видно из (6.11), отношение
R
R прямо пропорционально радиусу
проводника. Поэтому для уменьшения сопротивления проводника
переменному току целесообразно вместо цилиндрического проводника
использовать совокупность тонких изолированных друг от друга
проводников.
Пример: для серебряного проводника сечением 2 мм2 а=0,8 мм.
Тогда:
R
27.
R
Такое же сечение можно реализовать с помощью 4-х проводников
с а=0,4 мм. В этом случае
R
3.3.
R
* *