Проводники в переменных полях

1.

Проводники в переменных полях

2.

ДИЭЛЕКТРИКИ
ПОЛЯРНЫЕ
НЕПОЛЯРНЫЕ
+
+
+
-
-
kTB, Е≠0
P≠0
kTB, Е=0
-
-
+
+
+
Е
+ - +
+ +
+ + +
-
+
kTB, Е=0
+- +++ +
+P=0
P=0
-
+-
Е
+ -
+
+
+
+
+
-
-
+
+
-
P≠0
-
kTB, Е≠0

3.

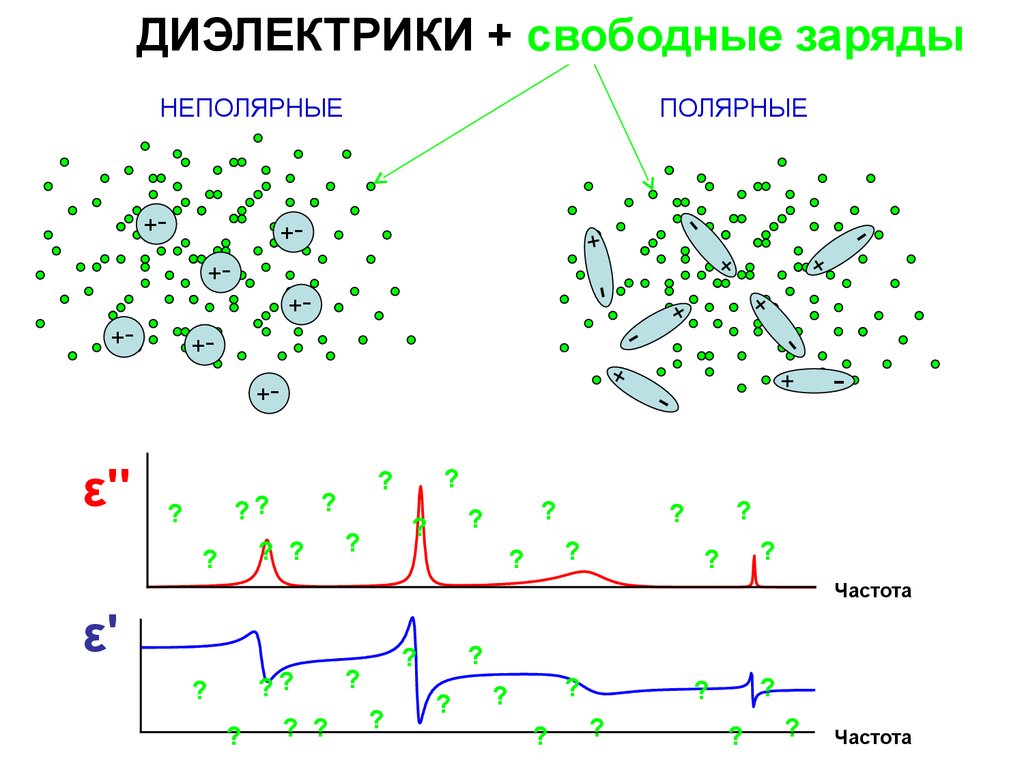
ДИЭЛЕКТРИКИ + свободные заряды
НЕПОЛЯРНЫЕ
+-
ПОЛЯРНЫЕ
+
?
?
?
?
-
? ?
?
+
-
-
?
?
?
??
?
+
+
-
+-
+
+
++-
ε''
-
+
++-
-
+-
?
?
?
?
?
?
Частота
ε'
??
?
?
? ?
?
?
?
?
?
?
?
?
?
?
?
?
?
Частота

4.

Проводники – свободные носители заряда (тока).
Модель среды - проводника:
пусть - электроны
Предположения:
1.
2.
3.
4.
Независимые друг от друга (невзаимодействующие).
Классические уравнения движения.
«Сила трения» - сопротивление (фононы, магноны, примеси, дефекты, …).
Электронейтральность, устойчивость системы
– положительные, неподвижные ионы в кристалле, подвижные ионы в плазме.
в диэлектрике было:
Сила со стороны
внешнего поля
Уравнение движения:
.
Сила «трения»
Возвращающая сила
сила со стороны
поля
Возвращающей силы нет (как было в диэлектриках)
сила «трения»
Туров 144

5.

Модель проводимости Друде
1900 г.
• Электроны – частицы классического газа.
• Электроны движутся свободно в решётке ионов.
• Движение – классические уравнения движения Ньютона.
• Электроны не взаимодействуют между собой.
• Электроны упругим образом, мгновенно, сталкиваются с:
решёткой ионов;
примесями;
дефектами и т.д.
• Электроны движутся с некоторой средней скоростью.
Пауль Друде
Германия
• Частота столкновений и масса электронов не зависят от их
скорости (от энергии).
+
+
-
+- - - +
+
- +
+
+ +
+
+
-+
+
+
+
++
-
-
+
-
-
-
l,
-
+ ионы
электронный
газ
l, - длина и время
свободного пробега

6.

В периодическом поле
Решение:
В диэлектрике было:

7.

Поляризуемость:
Проводник
Здесь:
- плазменная частота
= 1/ - частота столкновений (частота релаксации)

8.

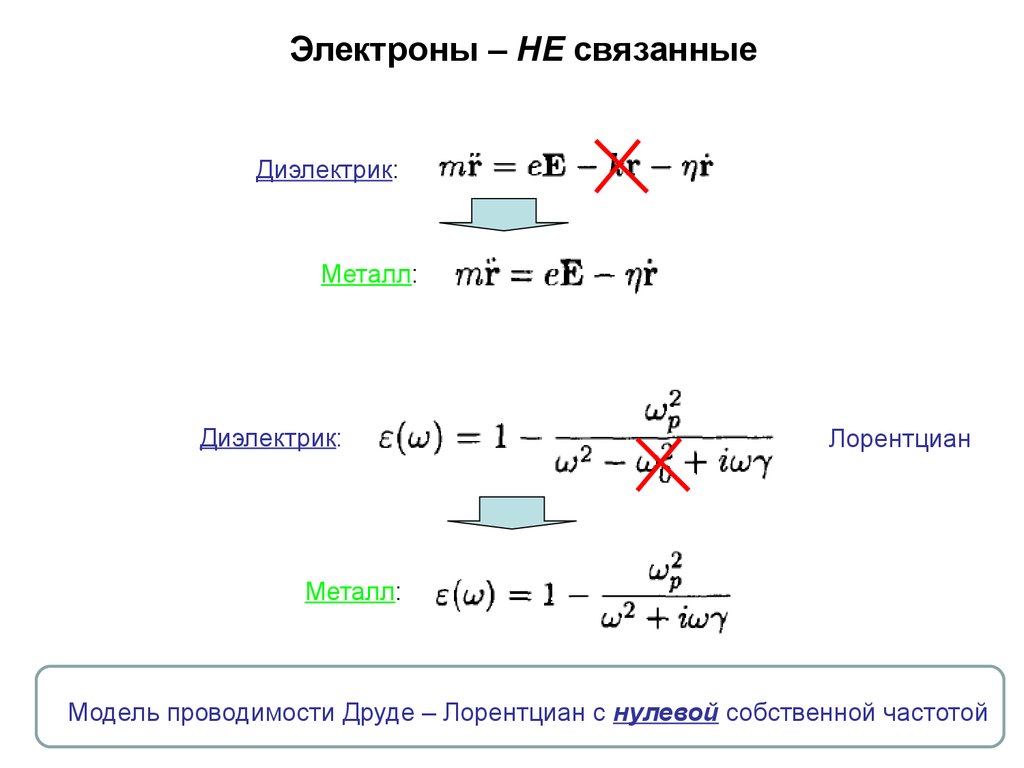
Электроны – НЕ связанные
Диэлектрик:
Металл:
Диэлектрик:
Лорентциан
Металл:
Модель проводимости Друде – Лорентциан с нулевой собственной частотой

9.

- комплексная величина: столкновения –
переход энергии в тепло – поглощение (энергия поля поглощается)
- адекватна описанию диэлектрика.
В случае проводника – не поляризуемость, а наведённые токи →
динамическая проводимость
.

10.

Физический смысл величины γ:
- статическая проводимость
При ω = 0:
Курс общей физики:
→
τ – время свободного пробега между соударениями
Вычисление
или - микроскопика.
Типичные величины:
медь
0≈106 Ом-1см-1 (СИ)
≈1018 Гц (СГСЭ)
≈10-13 с; ≈1013 Гц !

11.

Оптические свойства проводников
«Выделенные» частоты: γ и
γ
ωp. (Обычно ωp>>γ).
ωp
Особые области для проводника:
- «экранированная» плазменная частота
(смена знака
при ω>>γ)
Определяет длину волны в проводнике
Определяет затухание поля
ω

12.

γ
ωp
ω
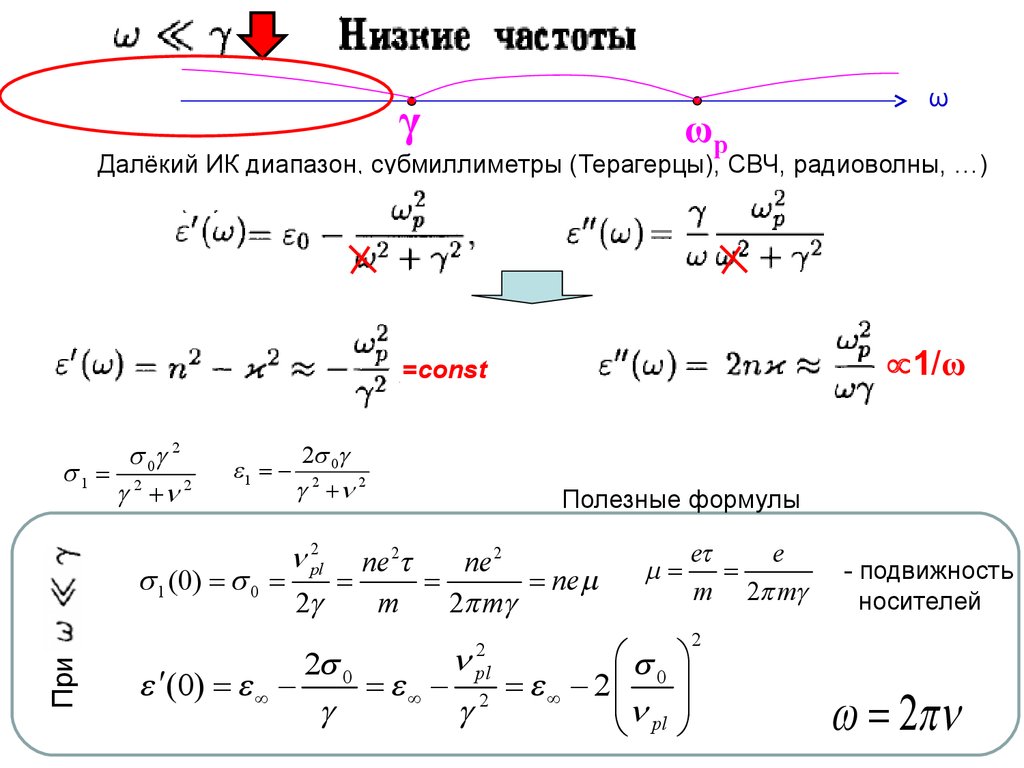
Далёкий ИК диапазон, субмиллиметры (Терагерцы), СВЧ, радиоволны, …)
1/ω
=const
0 2
1 = 2
n 2
e1 = -
2 0
2 n 2
Полезные формулы
При
n pl2 ne 2
ne 2
1 (0) = 0 =
=
=
= nem
2
m
2p m
m=
æ 0
n
2 0
e ¢(0) = e ¥ = e¥ = e¥ - 2ç
çn
è pl
2
pl
2
ö
÷÷
ø
e
e
=
m 2p m
- подвижность
носителей
2
w = 2pn

13.

Делим
на
т.е.:
Таким образом:
Металл, низкие частоты:

14.

Коэффициент отражения – предел Хагена-Рубенса
ω<<
[n(n ) - 1] 2 k (n ) 2
R(n ) =
[n(n ) 1] 2 k (n ) 2
Металл: n≈k>>1
2
n
R = 1- = 1- 2
n
n k
n
- формула Хагена-Рубенса
Эксперимент
Полезная формула
4n
n [cm -1 ]
R = 1= 1- 2
® 100%
-1
-1
30* [W cm ]

15.

γ
Делим
ωp
ω
на
n<<
или n>>
>>1
Поле НЕ проникает
в проводник (металл)

16.

было:
В случае низких частот
[n(n ) - 1]2 k (n ) 2
2
n
R(n ) =
R
=
1
=
1
2
® 100%
2
2
[n(n ) 1] k (n ) n ≈ k >> 1 и
n
ω<<
Е
много
столкновений
Поле не проникает в металл из-за высокого поглощения (ω<< ; n*k>>1)
<< k
[n(n ) - 1] 2 k (n ) 2
R (n ) =
[n(n ) 1] 2 k (n ) 2
R = 1-
Глубина проникновения поля:
>>1
4n
2
=
1
® 100%
2
k
wp
l
L=
<< l
2p k
Поле не проникает в металл из-за переотражённой волны (ω>> )
Лэнгмюровская экранировка (I.Langmuir).
rL – глубина лэнгмюровской экранировки
Irving Langmuir
1881-1957
США
rL не зависит от частоты
rL ≈ 10-5 – 10-6 см
Блеск металлов
Е
ω>>
мало
столкновений

17.

γ
ωp
ω
экранированная плазменная частота
Делим
<<1
на
n<<
или
<<n
- вещественная величина; поле НЕ затухает!

18.

- вещественная величина
k – мало, затухания НЕТ
Распространяются нормальные поперечные волны.
Закон дисперсии:
ω<ωpэкр. – металл НЕ прозрачен
ω >ωp экр. – металл прозрачен
П
«Запрещённые»
энергии
(ультрафиолетовая прозрачность металлов)
е
ны
ч
ре
е
оп
w=
ck
e¥

19.

Оптика металла (проводника)
γ
Поглощение
R≈100%
ωp
Отражение
R≈100%
Частота
Прозрачность
R<100%
1
0
Частота
e'
Частота

20.

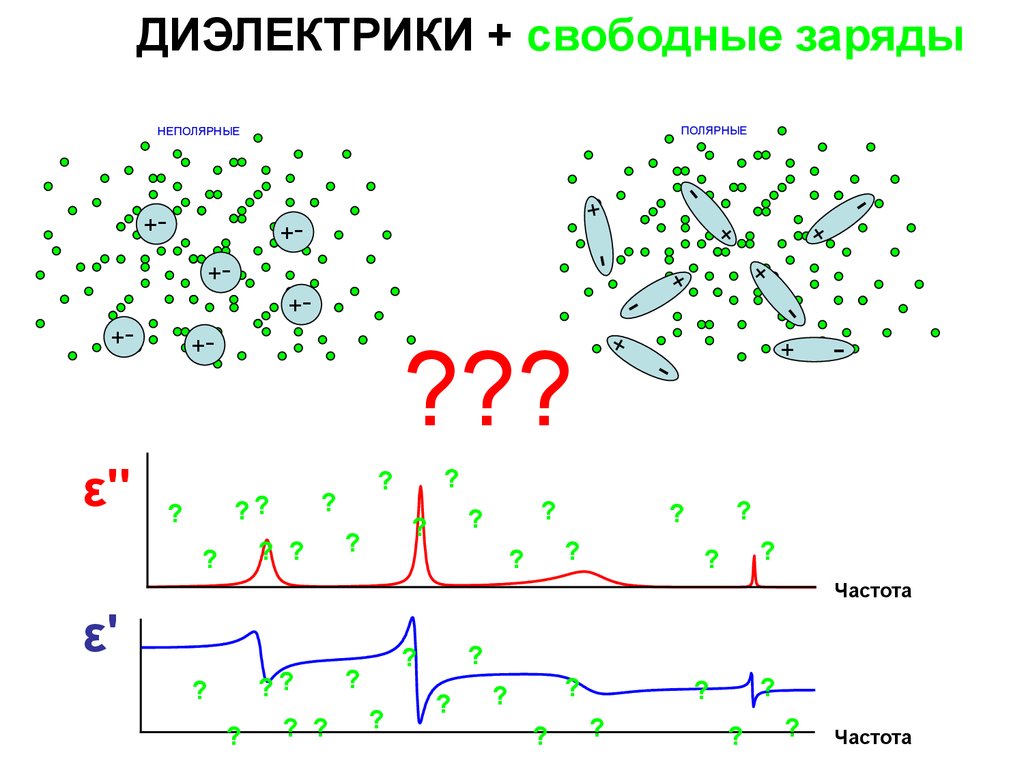
ДИЭЛЕКТРИКИ + свободные заряды
ПОЛЯРНЫЕ
-
НЕПОЛЯРНЫЕ
? ?
?
?
?
?
?
+
-
-
?
?
?
-
???
??
?
+
+
+-
-
+-
+
+
ε''
-
+-
+
++-
-
+
+-
?
?
?
?
?
?
Частота
ε'
??
?
?
? ?
?
?
?
?
?
?
?
?
?
?
?
?
?
Частота

21.

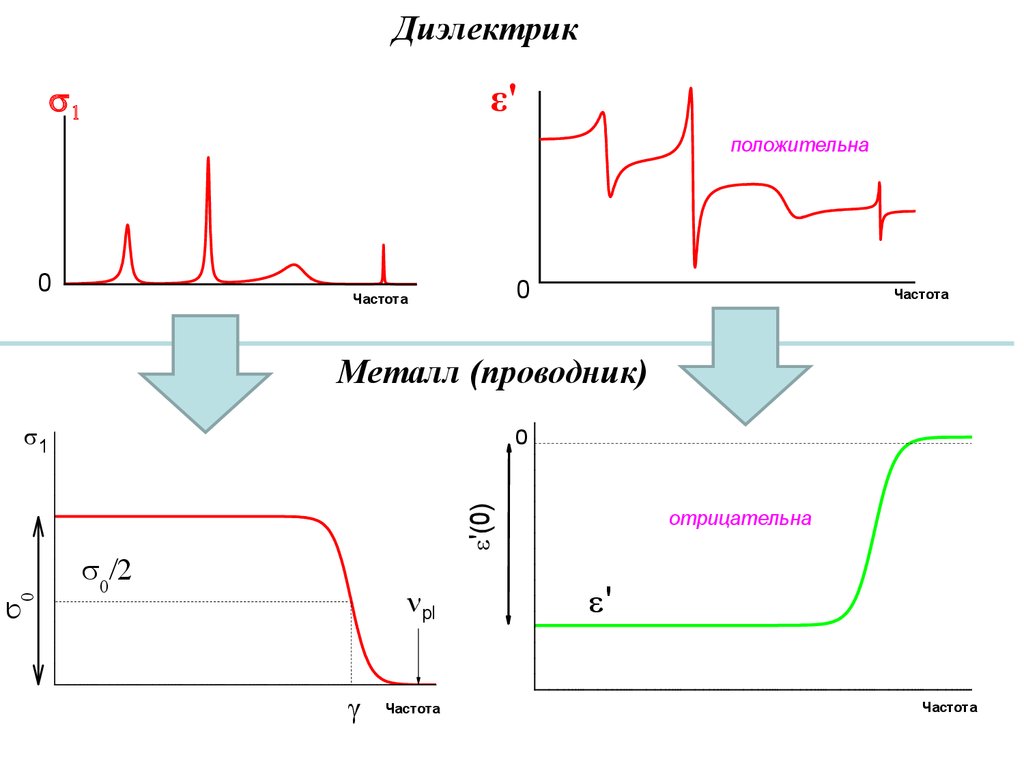
Диэлектрик
ε'
положительна
0
0
Частота
Частота
Металл (проводник)
1
e'(0)
0
npl
Частота
отрицательна
e'
Частота

22.

Характерные точки оптических спектров металлов
1
*= 1+i 2
2
отрицательно
e'(0)
0
e'
отрицательна
Хаген-Рубенс
R
0
wplэкр
1
1
npl
Частота
0
log(Частота)

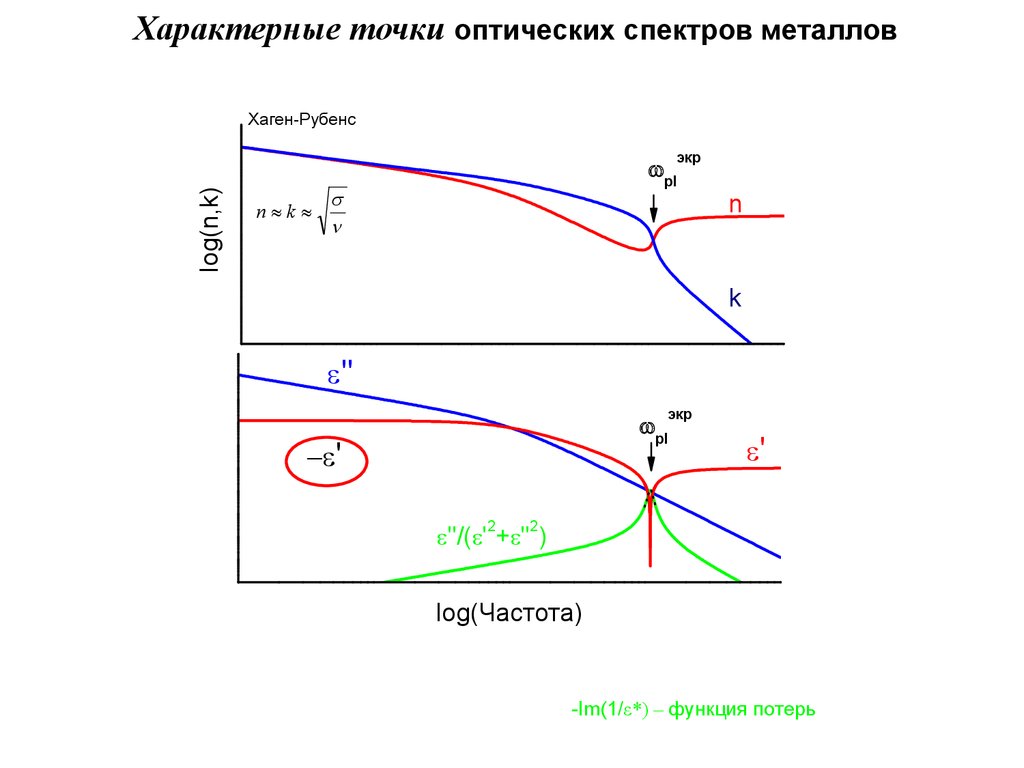
23.

Характерные точки оптических спектров металлов
Хаген-Рубенс
log(n,k)
экр
n k
wpl
n
n
k
e''
экр
wpl
-e'
2
e'
2
e''/(e' +e'' )
log(Частота)
-Im(1/ε*) – функция потерь

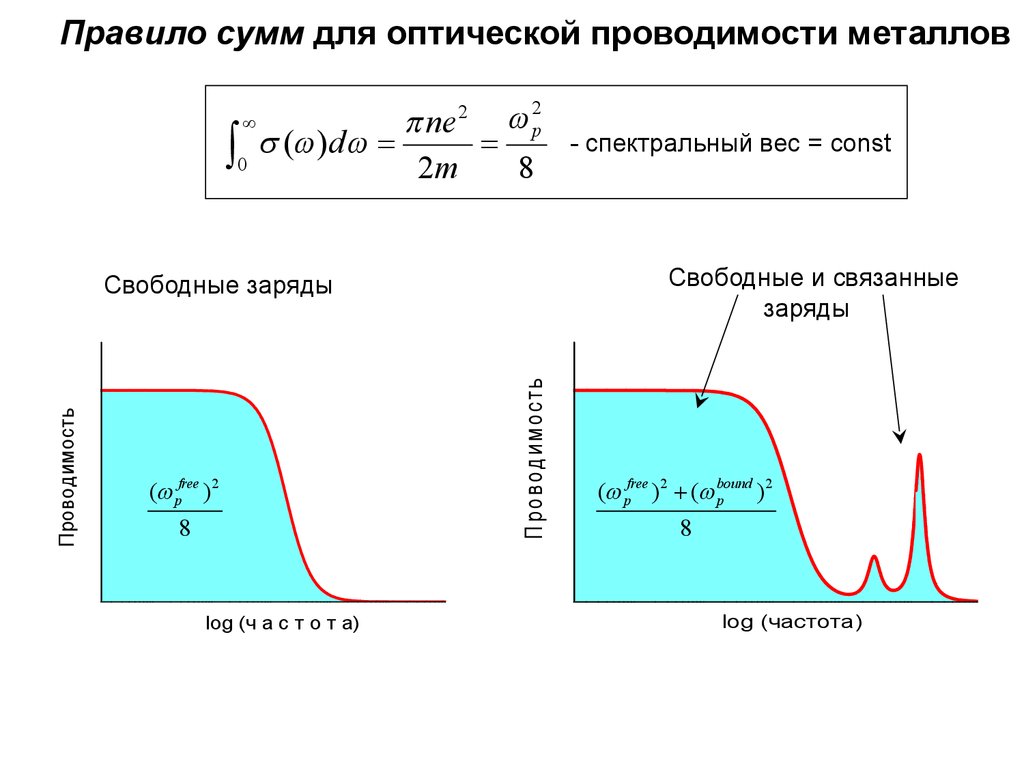
24.

Правило сумм для оптической проводимости металлов
ò
¥
0
2
p ne 2 w p
(w )d w =
=
2m
8
Свободные и связанные
заряды
8
log (ч а с т о т а)
П роводим ость
Проводимость
Свободные заряды
(w pfree ) 2
- спектральный вес = const
(w pfree ) 2 (w bound
)2
p
8
log (частота)

25.

аномальный
нормальный
пространственная дисперсия ЕСТЬ
Пространственной, временной дисперсии НЕТ
Амплитуда поля
exp(-δ/z)
z
l
n
1. Нет временнОй дисперсии ω<<γ.
2. Нет пространственной дисперсии:
(локальность взаимодействия)
Масштаб изменения поля
>>
масштаб характерного движения частицы.
d=
Направление распространения
Медь, T=300 К:
E(z)
0≈106 Ом-1см-1, ω≈1011 Гц →
δ ≈10
-5
δ
l << δ
l
δ>>l
l
E(z)
c
2p 0w
l
l
см = 0.1 мкм
l=10-6 см=0.01 мкм
электрона
l
l << δ
l
Туров 164

26.

Охлаждение:
0 растёт
d =
c
2p 0w
ne 2
ne2l
0 =
=
m
mv F
l=
mv F 0
ne 2
Медь, T=4.2 К: δ ≈10-6 см = 0.01 мкм; l=10-4 см=1 мкм; l >> δ
Нарушение локальности взаимодействия – аномальный скин-эффект
материальное уравнение
Точное решение: уравнения Максвелла – модель металла
в условиях нелокальности взаимодействия.
Более просто: модель эффективных и НЕэффективных электронов
(A.B.Pippard)
l
δ
l
l
l
l
l << δ l
нормальный скин-эффект
δа
l
Н
Еэ
Концепция
НЕэффективности
ф
ф
ек
т
ив
н
l
ы
е
эффективные
l >> δа!
Локальность (!)
взаимодействия
нелокальность взаимодействия
Эффективные электроны на длине l чувствуют поле
и ответственны за экранирование. Учёт – локальность.
НЕэффективные электроны – не учитываются.

27.

Все направления движения электронов равновероятны
E(z)
плотность эффективных электронов neff =
нормал
ьный
neff = nполн (δa/l)
α n (δa/l)
(α ≈1, зависит от типа рассеяния на границе. α=8/9 – зерк. расс.; α=1 – дифф. расс.)
ый
аномальн
E(z)
eff =
neff e 2
m
Z
d
ne 2 ad a
=
= a a 0
m l
l
1/ 3
æ l ö
d a = d norm ç
÷
ad
è norm ø
c
c
da =
=
2p eff w
2pad a 0w / l
d =
Свойства:
1.l >> δnorm → δa >> δnorm
2. Иная частотная зависимость
1/ 3
æ c 2l ö
3. d a = ç
÷
è 2pa 0w ø
0 =
1/ 3
æ c2m l ö
=ç
÷
2
è 2pa e nw ø
ne
m
2
VF
d a ~: w -1/ 3
1/ 3
æ c2m
ö
=ç
v
F ÷
2
è 2pa e nw ø
скорость Ферми
d норм =
1/ 3
æ cl ö
=ç
÷
2
p
wa
0
è
ø
2
c
2p 0w
c
w -1/ 2
2p 0w
независимость от температуры
только фундаментальные хар-ки

28.

Проводники
скин-слой
взаимодействие с полем определяется поверхностью
поверхностное сопротивление (поверхностный ИМПЕДАНС)
J y = E y ( z = 0) =
1
E y ( z = 0)
Z
Определение:
¥
J y = ò j y ( z )dz
0
Размерность: Ом
Z – поверхностное сопротивление (импеданс)
1/Z=σ – поверхностная проводимость
Z=
E y ( z = 0)
Jy
= Rs iX s
Z – комплексная величина
Rs – поглощение энергии излучения
Xs – сдвиг вазы между полем и током

29.

Импеданс плёнок
* = 1 i 2
B
Тонкие (d<<δ) плёнки
x
E
Z=
z
E y ( z = 0)
Jy
y
Z film = R
Rsfilm =
S
film
iX
S
film
¥
J y = ò j y ( z )dz * E y d
0
1
1
=
=
( 1 - i 2 )
2
2
* d d ( 1 2 )
1
X sfilm =
d ( 12 22 )
Низкочастотный предел Друде: 1>> 2≈ 0:
1
2
Частота
npl
l
1
=
, X sfilm = 0
1d
Общий случай для плёнки
d
b
d ( 12 22 )
film
s
R
2
Z film
2
ìï d ipw * üï
l æ 4p iw ö
= ç 2 ÷ coth í
ý
2b è c * ø
c
ïî
ïþ

30.

Нормальный-аномальный скин-эффект
Rs =
4p
n
c n2 k 2
Xs =
4p
k
c n2 k 2
Нормальный скин-эффект (ω<<γ)
Друде, низкочастотный предел
n k
>> 1
n
d =
c
2p 0w
Z norm
2pwd
2pw
= 2 (1 - i ) = 2 (1 - i )
c
c 0
2pwd
2pw
1/ 2
RS = - X S =
=
:
w
~
2
2
c
c 0
Действительная и мнимая части:
- равны;
- противоположны по знаку;
- пропорциональны w
Туров 175

31.

Аномальный скин-эффект
Z norm =
d norm
Za =
2pwd norm
(1 - i )
2
c
(ω<<γ)
1/ 3
æ cl ö
Þ da = ç
÷
2
pa
w
0
è
ø
2
1/ 3
1/ 3
2pwd a
2p æ c w l ö
2p æ c w v F mö
(1
i
)
=
(1-i)
=
ç
÷
ç
÷
c2
c 2 è 2pa 0 ø
c 2 è 2pa ne 2 ø
2
2
2
2
(1 - i ) :~ w 2 / 3
0
ne 2
=
m
Действительная и мнимая части:
- равны;
- противоположны по знаку;
- зависят лишь от фундаментальных характеристик;
- пропорциональны w 2 / 3
Более последовательная теория (аномальный скин-эффект): Rs= - 3 Xs

32.

Частотная зависимость поверхностного импеданса
Хаген-Рубенс,
ω << γ
n=k
RS=-XS
экр
n
n,k
wpl
k
Частота
Dressel/Gruner