Теория вероятности. Основные формулы

1.

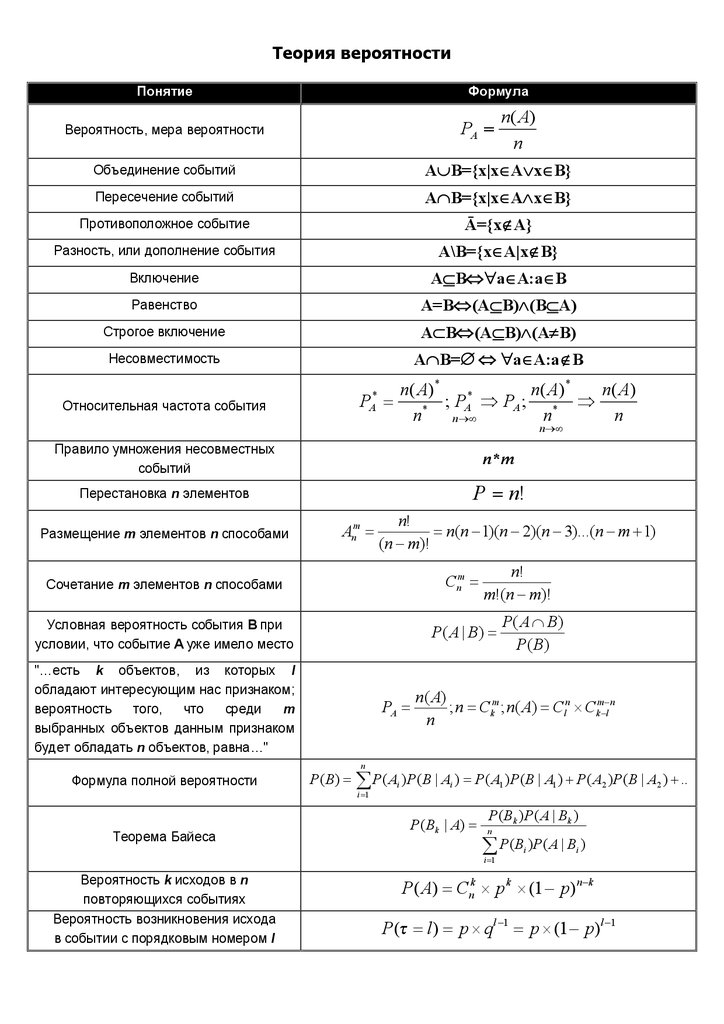
Теория вероятности
Понятие
Формула
PA =
Вероятность, мера вероятности
n( A)
n
Объединение событий
AÈB={x|xÎAÚxÎB}
Пересечение событий
AÇB={x|xÎAÙxÎB}
Противоположное событие
Ā={xÏA}
Разность, или дополнение события
A\B={xÎA|xÏB}
Включение
AÍBÛ"aÎA:aÎB
Равенство
A=BÛ(AÍB)Ù(BÍA)
Строгое включение
AÌBÛ(AÍB)Ù(A¹B)
Несовместимость
AÇB=Æ Û "aÎA:aÏB
Относительная частота события
n( A)* *
n( A)*
n( A)
P =
; PA Þ PA ; * Þ
*
n
n
n
n®¥
*
A
n®¥
Правило умножения несовместных
событий
n*m
Перестановка n элементов
P = n!
Размещение m элементов n способами
Anm =
n!
= n(n - 1)(n - 2)(n - 3)...(n - m + 1)
(n - m)!
n!
m!(n - m)!
Сочетание m элементов n способами
Cnm =
Условная вероятность события B при
условии, что событие A уже имело место
P( A | B) =
"…есть k объектов, из которых l
обладают интересующим нас признаком;
вероятность
того,
что
среди
m
выбранных объектов данным признаком
будет обладать n объектов, равна…"
PA =
P( A Ç B )
P( B )
n( A)
; n = Ckm ; n( A) = Cln ´ Ckm--l n
n
n
Формула полной вероятности
P( B) = å P( Ai ) P( B | Ai ) = P( A1 ) P( B | A1 ) + P( A2 ) P( B | A2 ) + ..
i =1
Теорема Байеса
P( Bk | A) =
P( Bk ) P( A | Bk )
n
å P( B ) P( A | B )
i =1
i
i
Вероятность k исходов в n
повторяющихся событиях
P( A) = Cnk ´ p k ´ (1 - p ) n-k
Вероятность возникновения исхода
в событии с порядковым номером l
P(t = l ) = p ´ q l -1 = p ´ (1 - p )l -1

2.

Математическая статистика
Понятие
Формула
Размах
R = max(x1;x2;…;xn)-min(x1;x2;…;xn)
X =
Среднее арифметическое
( X + X 2 + X 3 + ... + X n )
1 n
Xi = 1
å
n i =1
n
1 n
D=
( X i - X )2
å
n - 1 i =1
Дисперсия
s =
Стандартное отклонение
Коэффициент линейной корреляции
1 n
( X i - X )2
å
n - 1 i =1
å (x - x ) × ( y - y )
å (x - x ) × å ( y - y )
rx , y =
i
i
2
2
i
;
df = n - 2
i
( )
n × (n - 1) ;
6 × å D2
Коэффициент ранговой корреляции
r =1-
Коэффициент частной корреляции
rxy - z =
df = n
2
rxy - rxz × ryz
(1 - r )× (1 - r )
2
xz
2
yz
n1 × n2 × (n1 + n2 - 2 ) × ( x - y )
2
2
x
x
+
y
y
× (n1 + n2 )
(
)
(
)
å i
å i
2
t-критерий Стьюдента (в общем случае)
t=
(
t=
t-критерий Стьюдента для независимых групп
)
x-y
(n1 - 1) × s 12 + (n2 - 1) × s 22 × n1 + n2
n1 + n2 - 2
n1 × n2
df = n1 + n2 - 2
t-критерий Стьюдента для зависимых групп
Одновыборочный t-критерий Стьюдента
F-критерий Фишера
t=
å (x - y )
i
i
n × σ ( xi - y i )
t= n×
;
df = n - 1
x-A
σ ; df = n - 1
max( D1; D2 )
F=
min( D1; D2 ) ;
df1 = nmax – 1; df2 = nmin - 1
;