Материальные уравнения линейной электродинамики

1. Материальные уравнения линейной электродинамики

Скорости электронов |v| << c. Поэтому основной вклад
в эл. индукцию вносит эл. поле Е (а не Н).
t
3
Di (t , r ) = å ò dt ¢ò dr¢e ij (t , t ¢, r, r¢) E j (t ¢, r¢),
j =1 -¥
3
t
Bi (t , r ) = å ò dt ¢ò dr¢mij (t , t ¢, r, r¢) H j (t ¢, r¢),
j =1 -¥
3
t
ji (t , r ) = å ò dt ¢ò dr¢s ij (t , t ¢, r, r¢) E j (t ¢, r¢).
j =1 -¥
Среда неоднородна, нестационарна, анизотропна,
отклик нелокальный и немгновенный

2. Стационарная и однородная среда

R = r - r¢, t = t - t ¢
3 ¥
Di (t , r ) = å ò dt ò dR e ij (t , R ) E j (t - t , r - R ),
j =1 0
3 ¥
Bi (t , r ) = å ò dt ò dR mij (t , R ) H j (t - t , r - R ),
j =1 0
3 ¥
ji (t , r ) = å ò dt ò dR s ij (t , R ) E j (t - t , r - R ).
j =1 0

3. Электрическая и магнитная индукция

D = E + 4p P, B = H - 4p M
3 ¥
Pi (t , r ) = å ò dt ò dR k ij (t , R ) E j (t - t , r - R ),
j =1 0
3 ¥
M i (t , r ) = å ò dt ò dR n ij (t , R ) H j (t - t , r - R ).
j =1 0
Вещественные функции
e ij (t , R ), mij (t , R ), s ij (t , R ), k ij (t , R ),n ij (t , R )

4. Фурье-разложение (спектр плоских монохроматических волн)

¥
F (t , r ) =
¥
ò dk ò dw F(w, k ) exp[i(kr - wt )],
-¥
F = E, D, B, j
-¥
3
Di (w , k ) = å e ij (w , k ) E j (w , k ),
j =1
3
Bi (w , k ) = å mij (w , k ) H j (w , k ),
j =1
¥
e ij (w , k ) = d ik + 4p ò dt ò dR k ij (t , R ) exp[ -i(kR - wt )],
0
¥
mij (w , k ) = d ik + 4p ò dt ò dR n ij (t , R ) exp[ -i(kR - wt )]
0

5. Пространственная и частотная дисперсия

Вещественные функции
e ij (t , R ), mij (t , R ), s ij (t , R ), k ij (t , R ),n ij (t , R )
Комплексные функции
e ij (w , k ), mij (w , k )
Зависимость свойств среды от ω и k выражает, соответственно,
частотную (временную) и пространственную дисперсию.
Частотная дисперсия отражает наличие характерных
(резонансных) частот в среде, например, частот переходов между
электронными уровнями. Пространственная дисперсия служит
проявлением характерных пространственных размеров
«микроструктуры» сплошной среды, например, размеров атомов.
Обычно более важна роль частотной дисперсии.

6. Частотная дисперсия

В пренебрежении пространственной дисперсией
3
3
j =1
j =1
Di (w , r ) = å e ij (w ) E j (w , r ), Bi (w , r ) = å m ij (w ) H j (w , r ).
3
Для изотропной среды
3
Di (w , r ) = å e ij (w ) E j (w , r ), Bi (w , r ) = å m ij (w ) H j (w , r ).
j =1
j =1
Электрические свойства среды характеризуется скалярной функцией
¥
e (w ) = 1 + 4p ò k (t ) exp(iwt ) dt .
0
Функция κ(τ) вещественна и конечна при любых τ.
В среде с конечной проводимостью s 0 отклик среды на
монохроматическое электромагнитное поле можно характеризовать
не двумя величинами – ε, ϭ, а единой величиной – комплексной
диэлектрической проницаемостью:

7. Комплексная диэлектрическая проницаемость

s (w )
e (w ) = e (w ) + 4ip
w
(c)
rot H =
1 ¶D 4p
+
j
c ¶t
c
Монохроматическое излучение, временная зависимость
e
w
4p
w
4p
w (c)
rot H = -i D +
s (w )E = -i e + i s (w ) E = -i e E
c
c
c
w
c
div E = 4p .
4p
4p = -i
div(sE)
w
4p
div D - 4p = div e + i
s E = div(e (c) E) = 0
w
При высоких частотах
(c )
e
(w ) = 1
lim
w ¥
- iw t

8. Аналитические свойства диэлектрической проницаемости

¥
e (w ) = 1 + 4p ò k (t ) exp(iwt ) dt
Im k = 0
0
e (-w ) = 1 + 4p ò k (t ) exp(-iw t ) dt = 1 + 4p ò k (t ) exp(iwt ) dt = e (w )
e (-w ) = e (w )
e = e ¢ + ie ¢¢
e 1 (w ) e (w ) - 1 0
e ¢(-w ¢) = e ¢(w ¢),
e ¢¢(-w ¢) = -e ¢¢(w ¢).
w ¥ (w ¢¢ = Im w ³ 0)
s =0
При w ¢¢ ³ 0 функция ε(ω) однозначная и конечная (без особых
точек в верхней полуплоскости комплексных частот):
| exp(iwt ) | = | exp(iw ¢t ) exp( -w ¢¢t ) | < 1

9. Из теории функций комплексной переменной. Производная и аналитичность

z = x + iy, f ( z ) = u ( x, y ) + iv ( x, y ),
u ( x, y ) = Re f , v( x, y ) = Im f
df
f ( z + Dz ) - f ( z )
Производная комплексной функции
= lim Dz 0
dz
Dz
если такой предел существует (не
зависит от способа стремления к 0 Δz)
Условия существования производной:
df ¶f ¶u ¶v
=
=
+i .
dz ¶x ¶x
¶x
¶u ¶v
df
df
2. Dz = iDy,
= -i
= -i + i .
dz
dy
¶y
¶y
1. Dz = Dx,
¶u ¶v ¶v
¶u
= ,
=- .
¶x ¶y ¶x
¶y
- условия Коши-Римана
Аналитическая в некоторой области функция –
обладает производной df/dz в этой области

10. Из теории функций комплексной переменной. Интеграл. Теорема Коши

z = x + iy ,
f ( z ) = u ( x, y ) + iv ( x, y ), u ( x, y ) = Re f , v( x, y ) = Im f
Интеграл от комплексной функции по
контуру С сводится к двум интегралам
от вещественных функций:
ò f ( z) dz = ò (u + iv) (dx + idy ) =
C
C
= ò (udx - vdy ) + i ò (udy + vdx)
C
C
Теорема Коши: Если функция f(z) аналитична в односвязной
области D и кривые С расположены в этой области и имеют
общие концы, то интеграл ò f ( z) dz имеет одно и то же значение.
C
Вещественный интеграл по контуру не зависит от пути
интегрирования, если подынтегральное выражение - полный
¶S
¶S
дифференциал
( Pdx + Qdy ) = dS P =
,Q =
- условия Коши-Римана
¶u ¶v ¶v
¶u
= ,
=- .
¶x ¶y ¶x
¶y
ò
C
ò
C
¶2S
¶2S
¶P ¶Q
=
=
¶x¶y ¶y¶x
¶y ¶x
¶x
¶y

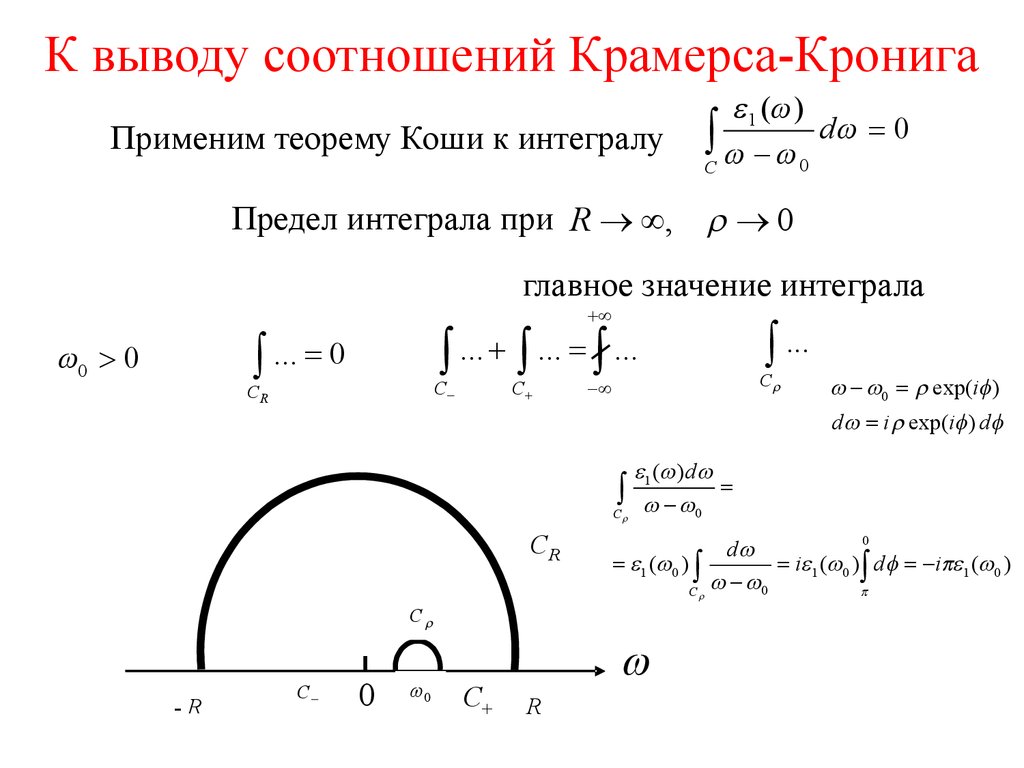
11. К выводу соотношений Крамерса-Кронига

Применим теорему Коши к интегралу
e 1 (w )
òC w - w 0 dw = 0
Предел интеграла при R ¥, 0
главное значение интеграла
+¥
ò ... + ò ... = ò ...
ò ... = 0
w0 > 0
C-
CR
C+
-¥
ò ...
C
w - w0 = exp(if )
d w = i exp(if ) df
e1 (w )d w
òC w - w0 =
CR
dw
= e1 (w0 ) ò
= ie1 (w0 ) ò df = -ipe1 (w0 )
w
w
0
C
p
0
C
-R
C-
0
w0
C+
w
R

12. Cоотношения Крамерса-Кронига

¥
e (w ) d w
ipe1 (w0 ) = ò 1
-¥ w - w0
переобозначение e (w ) - 1 = 1
ip
переменных
¥
[e (n ) - 1] dn
ò-¥ n - w
Разделяем вещественную и мнимую части
1
e ¢(w ) - 1 =
p
¥
¥
e ¢¢(n ) dn
1 [e ¢(n ) - 1] dn
ò-¥ n - w , e ¢¢(w ) = - p -¥ò n - w
Для проводника последнее соотношение включает
дополнительное слагаемое в правой части 4ps / w

13. Энергия электромагнитного поля в среде с частотной дисперсией

Для вакуума плотность потока электромагнитной энергии
определяется вектором Пойнтинга:
c
S=
[E H ] .
4p
Эта же формула справедлива и в средах с дисперсией ввиду
непрерывности тангенциальных составляющих E и H на границе
раздела среды с вакуумом.
Изменение электромагнитной энергии в единице объема за единицу
времени
- div S =
c
1 ¶D
¶B
[(E, rot H ) - (H, rot E)] =
E
+
H
.
4p
4p ¶t
¶t
В отсутствие дисперсии, когда материальные уравнения имеют простейший
вид с постоянными вещественными e и m, отсюда следует выражение для
плотности электромагнитной энергии U:
1
U=
(eE 2 + mH 2 ).
8p

14. Энергия э.-м. поля при наличии частотной дисперсии

В общем случае, присутствует и диссипация энергии
(переход энергии электромагнитного излучения в тепло).
Закон сохранения энергии
¶U
= -div S - Q,
¶t
Q – плотность энергии тепловых потерь. В случае произвольного
электромагнитного поля определение вида плотности энергии и
тепловых потерь затруднительно. Два частных случая:
1.
Монохроматическое электромагнитное поле с частотой w0. Для
него усредненное за период колебаний выражение
-div S =
1
4p
¶B
¶D
E
+
H
¶t
¶t
дает средний приток энергии от внешних источников,
преобразующийся в тепло, то есть Q. Здесь фигурируют
вещественные величины. Чтобы отличить их от комплексных
амплитуд снабдим вещественные величины знаком ~.

15. Энергия э.-м. поля при наличии частотной дисперсии*

~
E = Re[E exp(-iw 0 t )],
~
H = Re[H exp(-iw 0 t )],
~
D = Re[D exp(-iw 0 t )],
~
B = Re[B exp(-iw 0 t )].
При усреднении по времени члены, меняющиеся с удвоенной
частотой 2w0, обращаются в нуль. Поэтому
w0
Q=
[e ¢¢ | E | 2 + m ¢¢ | H | 2 ].
8p
Диссипация (поглощение) энергии определяется мнимыми
частями диэлектрической и магнитной проницаемостей. Для
термодинамически равновесных сред эти величины должны
быть положительными для всех (положительных) частот:
e ¢¢(w ) > 0, m ¢¢(w ) > 0.
Вещественные части проницаемостей могут быть как положительными,
так и отрицательными.

16. Энергия э.-м. поля. Квазимонохроматическое излучение

1
-div S =
4p
¶B
¶D
E ¶t + H ¶t
~
E = Re[E exp(-iw 0 t )],
~
H = Re[H exp(-iw 0 t )],
~
D = Re[D exp(-iw 0 t )],
~
B = Re[B exp(-iw 0 t )].
После усреднения за период
1
- < div S >=
16p
¶D
¶
D
¶
B
¶B
E
+
E
+
H
+
H
+
¶t
¶t
¶t
¶t
iw 0
+
(ED - E D + HB - H B).
16p
Привлекаем материальные соотношения

17. Энергия э.-м. поля. Квазимонохроматическое излучение*

¥
D(t ) = E(t ) + 4p ò k (t ) E(t - t ) exp(iw 0t ) dt ,
0
¥
B(t ) = H (t ) + 4p òn (t ) H (t - t ) exp(iw 0t ) dt .
0
Учтем медленность изменения огибающих за время
релаксации, разложив напряженности в ряд по t:
¶E
¶H
E(t - t ) = E(t ) t + ..., H (t - t ) = H (t ) t + ...
¶t
¶t
¥
¥
¶E
¶e ¶E
D(t ) = 1 + 4p ò k (t ) exp(iw0t ) dt E(t ) - 4p ò tk (t ) exp(iw0t ) dt
= e (w0 )E(t ) + i
,
¶
t
¶
w
¶
t
w0
0
0
¥
¥
¶H
¶m ¶H
B(t ) = 1 + 4p òn (t ) exp(iw0t ) dt H (t ) - 4p ò tn (t ) exp(iw0t ) dt
= m (w0 ) H(t ) + i
.
¶w w0 ¶t
0
0
¶t

18. Энергия э.-м. поля. Квазимонохроматическое излучение*

¶D
¶E
= e (w 0 )
,
¶t
¶t
¶B
¶H
= m (w 0 )
.
¶t
¶t
w0
1 ¶ ¶ (we ¢)
2
2
2
- < div S >=
e ¢¢ | E | + m ¢¢ | H | +
|E|
8p
16p ¶t ¶w w
0
¶ (wm ¢)
2
+
|H| +
¶w w 0
¶ (we ¢¢)
¶E ¶ (wm ¢¢)
¶H
+
.
Im E
Im H
¶t
¶w w 0 ¶t ¶w w 0
Члены, описывающие изменение усредненной за основной период колебаний
плотности электромагнитной энергии, и тепловые потери в общем случае
разделить эти члены невозможно. Для монохроматического поля производные по
времени огибающих равны нулю, и получаем прежнее выражение.
Другой предельный случай относится к областям прозрачности среды:
1
+
8p
¶U
1 ¶ ¶ (we ¢)
¶ (wm ¢)
2
2
- < div S >=
=
| E | +
|H|
¶t 16p ¶t ¶w w0
¶w w0
1 ¶ (we ¢)
¶ (wm ¢)
2
2
Усредненная плотность
U=
| E | +
| H | .
16p ¶w w
электромагнитной энергии
¶w w
0
0

19. Ковариантная форма уравнений электродинамики сплошных сред

Для сплошной среды, в отличие от вакуума, требуется уже ввести не один
антисимметричный 4-тензор электромагнитного поля, а два (каждый из них в
ковариантном и контравариантном видах)
- Ex
0
- Bz
By
0
Ex
Fik =
E
y
E
z
0
Dx
Qik =
D
y
D
z
- Dx
0
- Hz
Hy
Диф. ур-ния
Максвелла
- Ey
Bz
0
- Bx
- Ez
0
- By
- Ex
ik
'
F
=
- E
Bx
y
- E
0
z
Ex
0
- Bz
By
Ey
Bz
0
- Bx
- Dy
Hz
0
- Hx
- Dz
0
- Hy
- Dx
ik
' Q =
Hx
- Dy
- D
0
z
Dx
0
- Hz
Hy
Dy
Hz
0
- Hx
¶Fik ¶Fkm ¶Fmi
+
+
=0
¶x m
¶xi
¶x k
Ez
- By
.
Bx
0
Dz
- Hy
.
Hx
0
¶Q ik
4p i
å ¶x = - c j
k =0
k
3

20. Материальные уравнения для движущихся тел

Тело движется в лабораторной системе со скоростью v.
Требуется получить вид материальных уравнений для
электрической и магнитной индукций движущегося тела.
В системе координат, движущейся вместе с изотропным
диэлектриком (отмечается штрихами), материальные уравнения
D' = eE' , B' = mH '.
Используя преобразования Лоренца, найдем, что в лаб. системе
тело становится анизотропным и поляризации зависят
как от электрической, так и от магнитной напряженностей.
Для компонент, параллельных и перпендикулярных скорости v,
получим (введен показатель преломления n 2 = em )
D|| = eE|| ,
v2
e 1 - 2
c
D =
B|| = mH || ,
n2 -1
E +
[ v H]
c
,
2 2
n v
1- 2
c
v2
m 1 - 2
c
B =
n2 -1
H [ v E]
c
.
2 2
n v
1- 2
c

21. Материальные уравнения для движущихся тел*

Недостаток вида материальных уравнений: при
n2 > 1
знаменатель может обращаться в 0. Возможное решение: выбор в качестве
независимых переменных для материальных соотношений величин E,B
D|| = eE|| ,
e
D =
v2
1- 2
c
H || =
n 2 v 2
1 - 2
c
n2 -1
E + 2 [ v B] ,
n c
1
B|| ,
m
n 2 v 2
n2 -1
H =
1
B
+
[
v
E
]
.
2
2
c
c
v
m 1 - 2
c
1
При малых скоростях движения среды n 2 v 2 / c 2 < 1
различие между этими двумя формами материальных соотношений исчезает.
Более полный анализ требует учета частотной дисперсии.
Приведенные соотношения описывают френелевское «частичное
увлечение» (опыты Физо). Материальными уравнениями Минковского
можно пользоваться не только при постоянной скорости движения тела, но
и при переменной скорости, если только ускорение достаточно мало.

22. Плоская монохроматическая волна

14_Lec_9_10.doc Плоская монохроматическая волна.
Импульс в среде с частотной дисперсией. Анизотропные
среды.
Lec_11.pdf Двойное преломление в эл. поле.
Магнитооптика. Пространственная дисперсия.
LEC_12a.pdf Волны в неоднородных средах. Геом. оптика.
Lec12b. Условия непрерывности.
Lec13 Плоскослоистые среды
Lec14a Планарный волновод. Волны в периодических
структурах
Lec_15 Градиентный волновод. Линзовые линии.
Резонаторы со сферическими зеркалами. Рассеяние на
малых частицах. Металлические волноводы.