Теорема Гаусcа та її застосування

1. ЕЛЕКТРИКА І МАГНЕТИЗМ Електронний курс лекцій

Укладач: Данилов А.Б.

2.

Лекція 15
Теорема Гаусcа
та її застосування.

3.

Всі науки можна класифікувати на дві
групи:
1. Фізика.
2. Колекціонування марок.
Ернест Резерфорд

4. План лекції

• Потік вектора напруженості електричного поля.
• Теорема Остроградського-Гаусса.
• Застосування теореми Остроградського-Гаусса
до розрахунку електричних полів.
• Теорема Гаусса у диференціальній формі.
• Робота сил електростатичного поля.

5.

Лекція 15
Теорема Гаусса
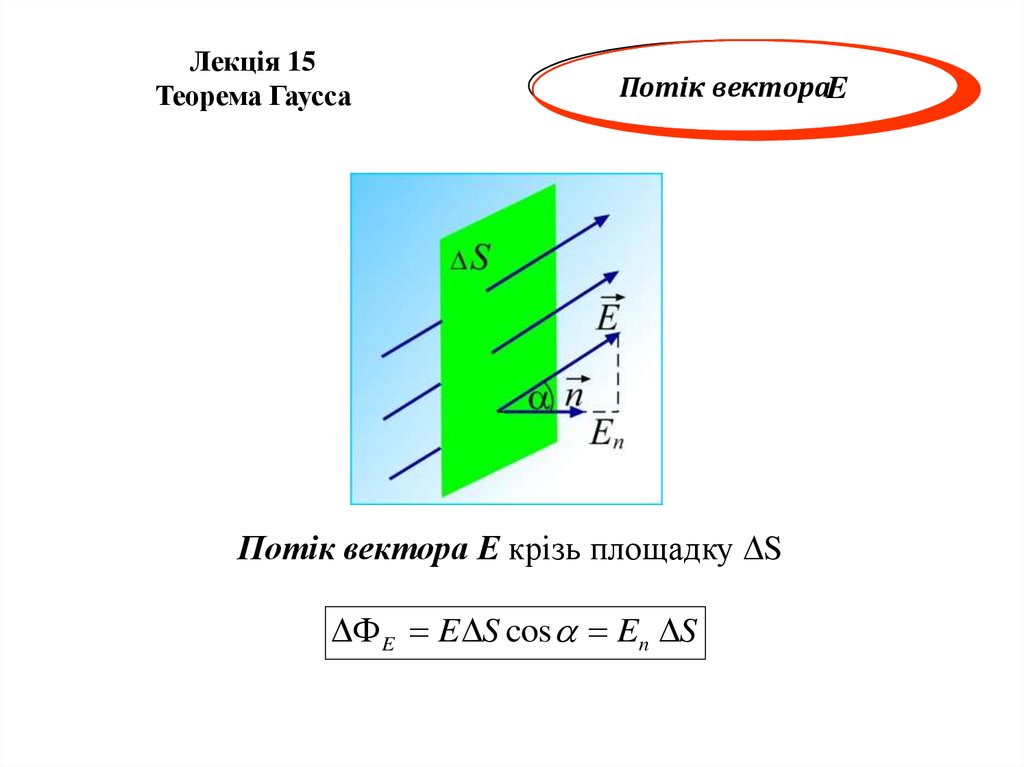
Потік вектораE
Потік вектора Е крізь площадку S
E E S cos En S

6.

Лекція 15
Теорема Гаусса
Потік вектора E
Елементарний електричний потік
d E En dS
Повний потік крізь поверхню S
E E n dS
S
d E En dS

7.

Лекція 15
Теорема Гаусса
Теорема Гаусса
Гаусс Карл Фрідріх,
(1777-1855)
Німецький математик і фізик.
Роботи з алгебри, теорії чисел,
диференціальної геометрії і теорії
чисел, електрики і магнетизму,
астрономії.

8.

Лекція 15
Теорема Гаусса
Теорема Гаусса
Потік вектора напруженості E
електростатичного поля у вакуумі
крізь довільну замкнену поверхню S
зсередини
назовні
дорівнює
алгебричній сумі тих точкових
qi
зарядів
, які охоплюються
поверхнею
S,
поділеній
на
електричну сталу .
0
E En dS
S
1
0
N
qi
i 1

9.

Лекція 15
Теорема Гаусса
Приклади
розрахунку полів за
Гауссом
Напруженість поля нескінченної площини
E
2 0

10.

Лекція 15
Теорема Гаусса
Приклади
розрахунку полів за
Гауссом
Напруженість поля
двох різнойменно заряджених площин

11.

Лекція 15
Теорема Гаусса
Приклади
розрахунку полів за
Гауссом
Напруженість поля
поблизу поверхні зарядженого провідника
E
0

12.

Приклади
розрахунку полів за
Гауссом
Лекція 15
Теорема Гаусса
Напруженість поля
нескінченної зарядженої нитки, довгого циліндра
Провідний циліндр радіуса R,
по якому заряд розподілено
рівномірно з лінійної густиною
Ззовні
E
2 0 r
Всередині E 0

13.

Лекція 15
Теорема Гаусса
Приклади
розрахунку полів за
Гауссом
Напруженість поля
нескінченної зарядженої нитки, довгого циліндра
E
2 0 r

14.

Приклади
розрахунку полів за
Гауссом
Лекція 15
Теорема Гаусса
Напруженість поля
нескінченного довгого діелектричного циліндра
Непровідний циліндр радіуса R, в якому заряд розподілено рівномірно з
об’ємною густиною
Ззовні циліндра
E ESб E 2 r h
1
0
Vнепров.ц .
1
0
R 2 h
Всередині циліндра
E ES б E 2 rh
Vдоп.ц.
0
r 2 h
0
R 2 h R 2
E
2 rh 0 2 0 r
r
E
2 0

15.

Лекція 15
Теорема Гаусса
Приклади
розрахунку полів за
Гауссом
Напруженість поля
нескінченного довгого діелектричного циліндра
R
E
2 0
r
E
2 0
R2
E
2 0 r

16.

Приклади
розрахунку полів за
Гауссом
Лекція 15
Теорема Гаусса
Напруженість поля
рівномірно зарядженої сфери
Провідна сфера:
Ззовн
і
E
q
4 0 r 2
Всередині E 0

17.

Лекція 15
Теорема Гаусса
Приклади
розрахунку полів за
Гауссом
Напруженість поля
рівномірно зарядженої сфери
E
q
4 0 r 2

18.

Приклади
розрахунку полів за
Гауссом
Лекція 15
Теорема Гаусса
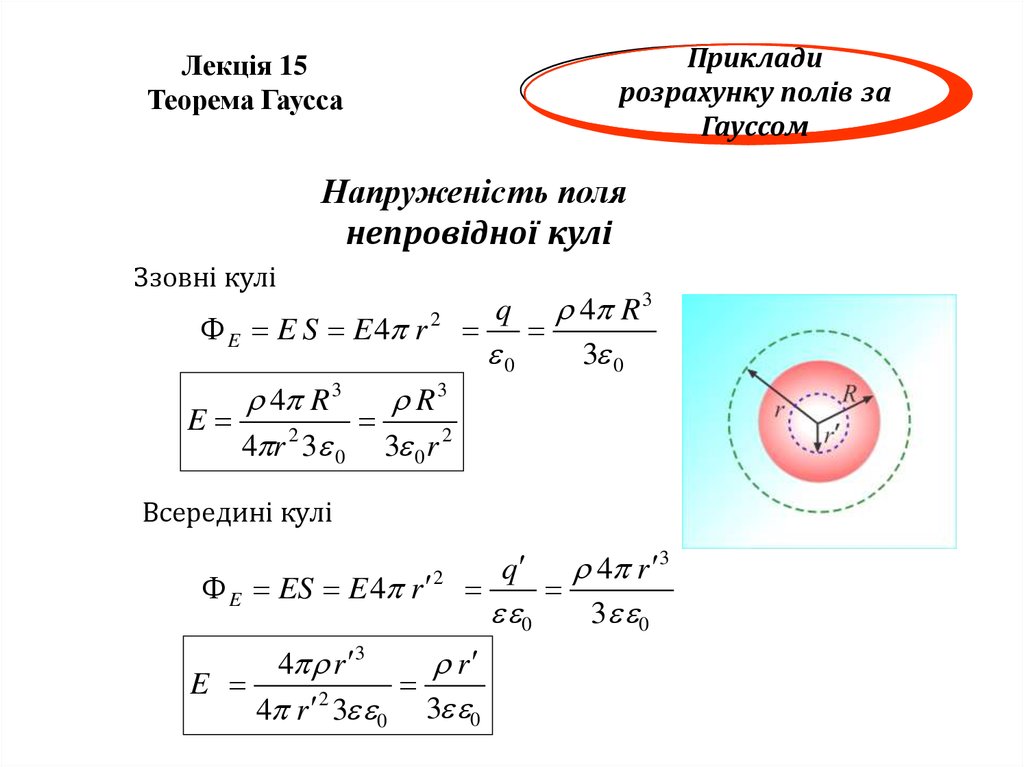
Напруженість поля
непровідної кулі
Ззовні кулі
E E S E 4 r 2
4 R 3
0
3 0
q
4 R 3
R3
E
2
4 r 3 0 3 0 r 2
Всередині кулі
4 r 3
E ES E 4 r
0
3 0
4 r 3
r
E
2
4 r 3 0 3 0
2
q

19.

Приклади
розрахунку полів за
Гауссом
Лекція 15
Теорема Гаусса
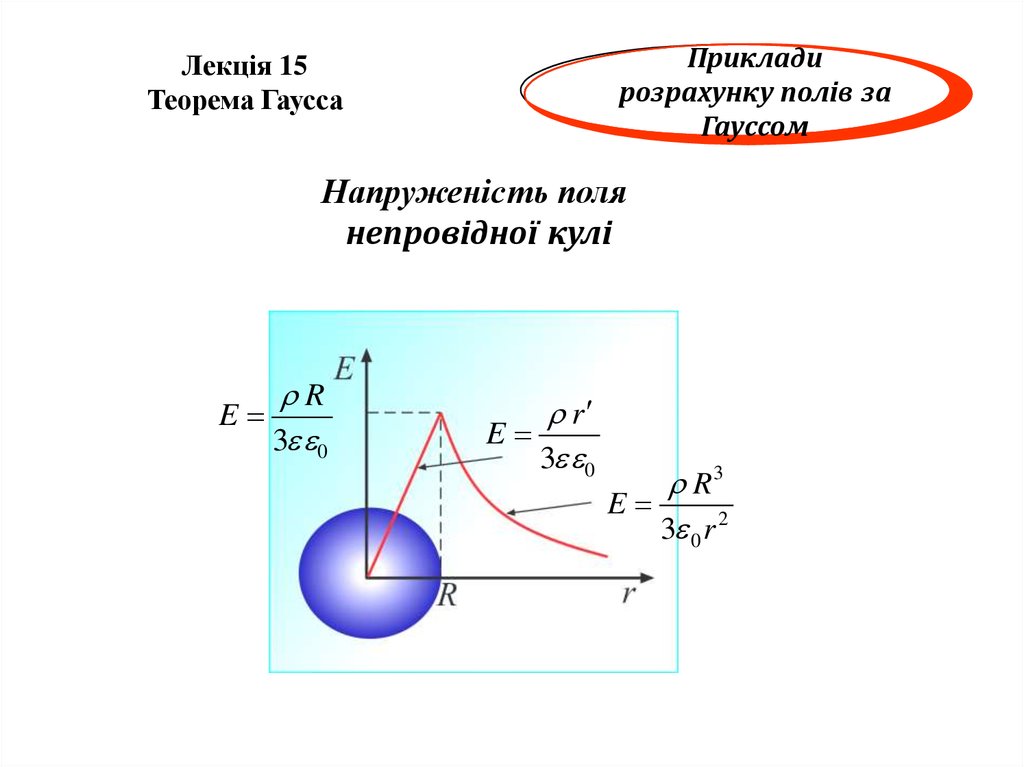
Напруженість поля
непровідної кулі
E
R
3 0
E
r
3 0
R3
E
3 0 r 2

20.

Лекція 15
Теорема Гаусса
Поняття дивергенції
Дивергенцією деякого векторного поля A(r ) називається
границя відношення
An dS
div A lim
V 0
S
V
У декартовій системі координат
Ax Ay Az
div A
x
y
z
div A ( A )
i
j k
x
y
z

21.

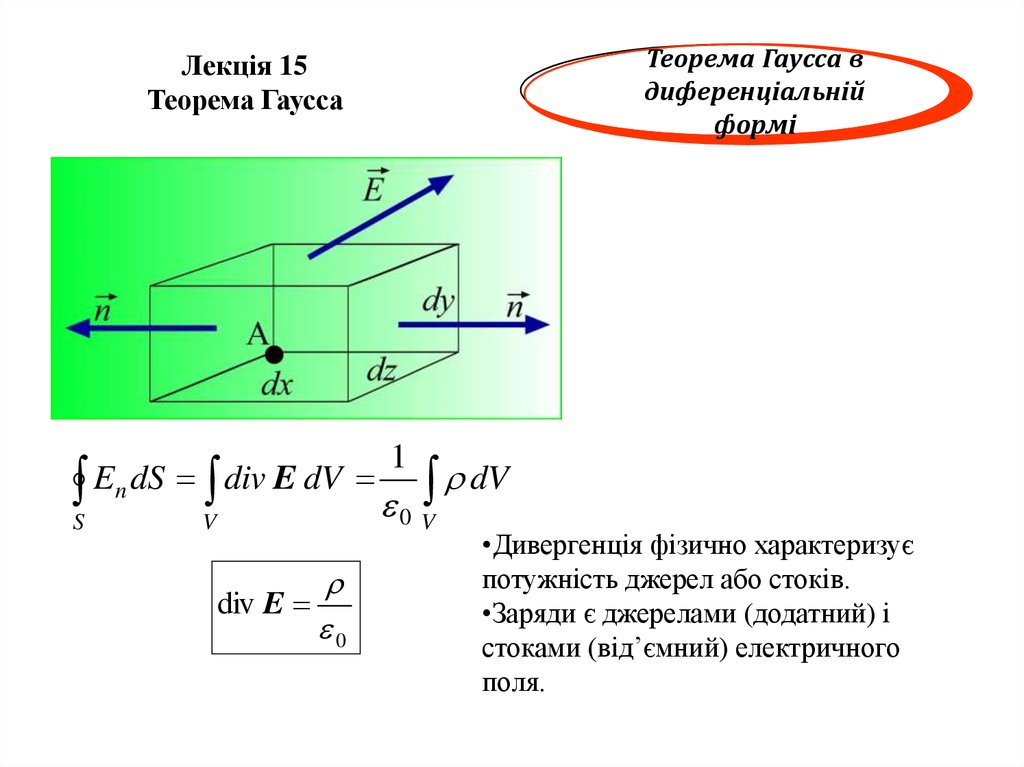
Теорема Гаусса в
диференціальній
формі
Лекція 15
Теорема Гаусса
q
r
En dS div E dV
S
V
1
dV
0
V
div E
0
•Дивергенція фізично характеризує
потужність джерел або стоків.
•Заряди є джерелами (додатний) і
стоками (від’ємний) електричного
поля.

22.

Робота сил
електростатичного поля
Лекція 15
Теорема Гаусса
•Елементарна робота сил
електростатичного поля
dA F dl Fdl cos q0 E dl cos
•Для поля точкового заряду
dA
q0 q dr
4 0 r 2

23.

Лекція 15
Теорема Гаусса
Робота сил
електростатичного поля
Робота сил електростатичного поля точкового заряду при
переміщенні в цьому полі пробного заряду з точки 1 в
точку 2:
r2
( 2)
( 2)
q0 q dr
q0 q 1 1
A1 2 dA q0 E dl
2
4 0 r r
4 0 r1 r2
(1)
(1)
1
Робота додатна, якщо:
- однойменні заряди
віддаляються;
- різнойменні заряди
Робота
від’ємна, якщо:
наближаються.
- різнойменні заряди віддаляються;
- однойменні заряди наближаються.

24.

Лекція 3
Потенціал
електростатичного
поля
Робота сил
електростатичного поля
Робота електростатичного поля не
залежить від форми шляху переміщення
заряду від точки 1 до точки 2, а
визначається
лише
положенням
початкової і кінцевої точки.
Силові поля, що задовольняють таку
умову, називаються потенціальними, або
консервативними

25.

26.

Дякую за увагу!