Задача 29

1.

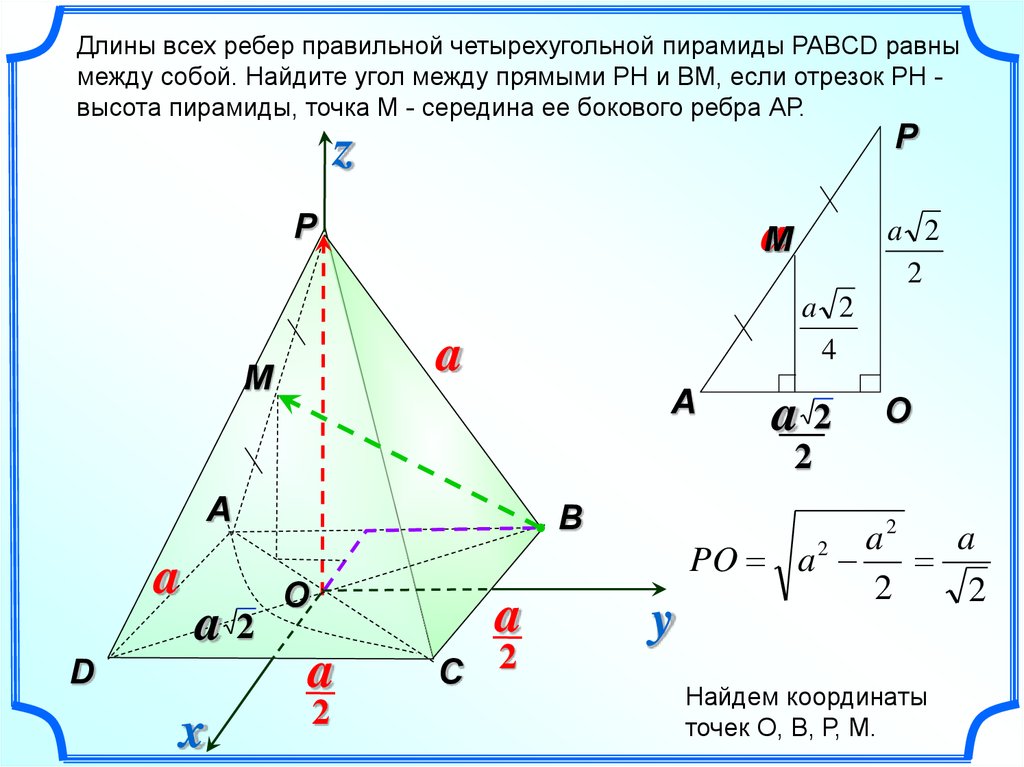
Длины всех ребер правильной четырехугольной пирамиды PABCD равны
между собой. Найдите угол между прямыми РН и ВМ, если отрезок РН высота пирамиды, точка М - середина ее бокового ребра АР.
P
z
P
aM
a 2
2
a 2
4
a
M
A
a
2
O
2
A
a
a2
B
O
a
a
D
x
2
C
2
y
2
a
a
2
PO a
2
2
Найдем координаты
точек О, В, Р, М.

2.

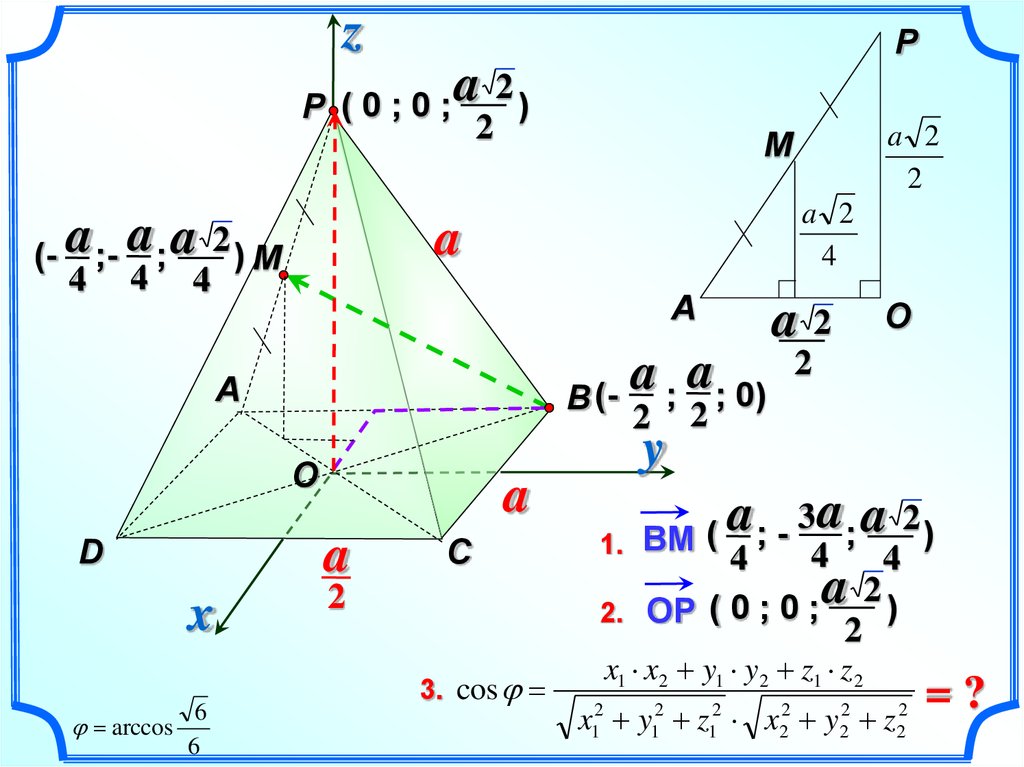
z
P
2
a
(
0
;
0
;
)
P
2
(- a ;- a ; a 2 ) M
4 4 4
A
O
a
D
x
6
arccos
6
a 2
4
a
A
2
C
a 2
2
M
a2
O
2
a
a
B (- ; ; 0)
2 2
y
a
3 a; a 2 )
a
(
;
1. BM
4
4
4
2
a
(
0
;
0
;
)
2. OP
2
3. cos
x1 x2 y1 y2 z1 z2
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2
=?