Построение перспективы методом архитекторов с опущенным (поднятым) планом

1. Лекция 20

Построение перспективы методом
архитекторов с опущенным (поднятым)
планом
•Построение опущенного плана
•Построение вертикальной вспомогательной
стенки

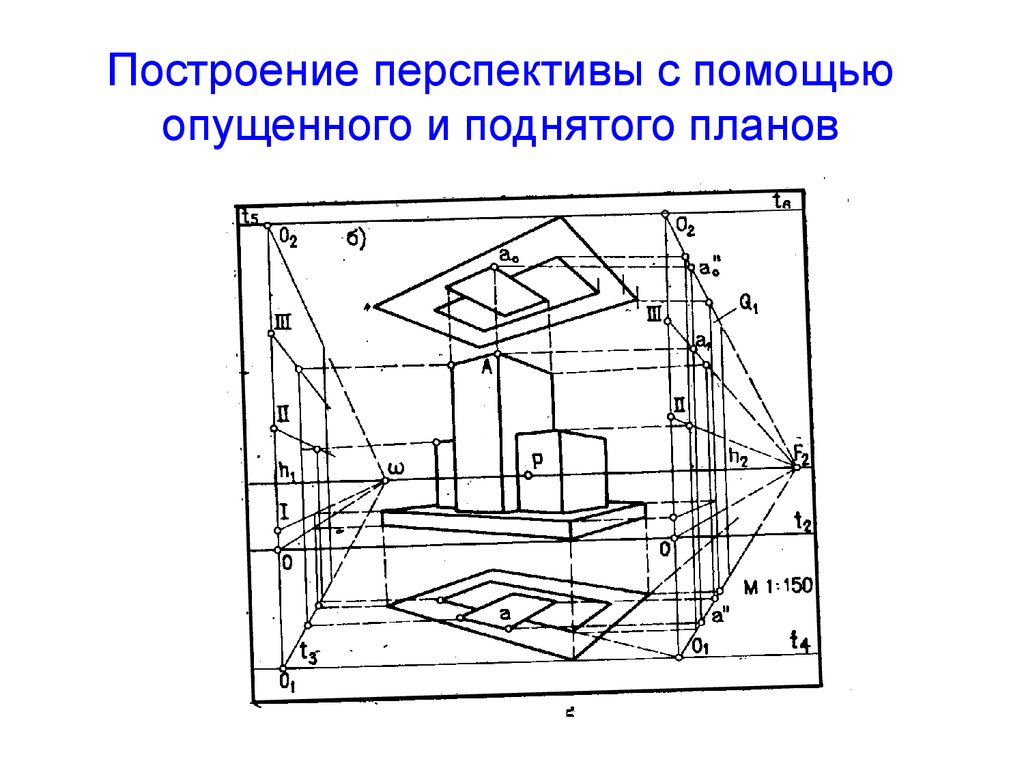
2. Построение перспективы с помощью опущенного и поднятого планов

3. Применение дополнительного плана

• В случаях, когда высота горизонта мала и
вторичная проекция объекта оказывается
сжатой, что затрудняет дальнейшие
построения на перспективе плана, применяют
горизонтальную вспомогательную плоскость.
• Перспективу плана строят не на предметной
плоскости, а на вспомогательной, опущенной
вниз от предметной плоскости на
произвольное расстояние или поднятой вверх

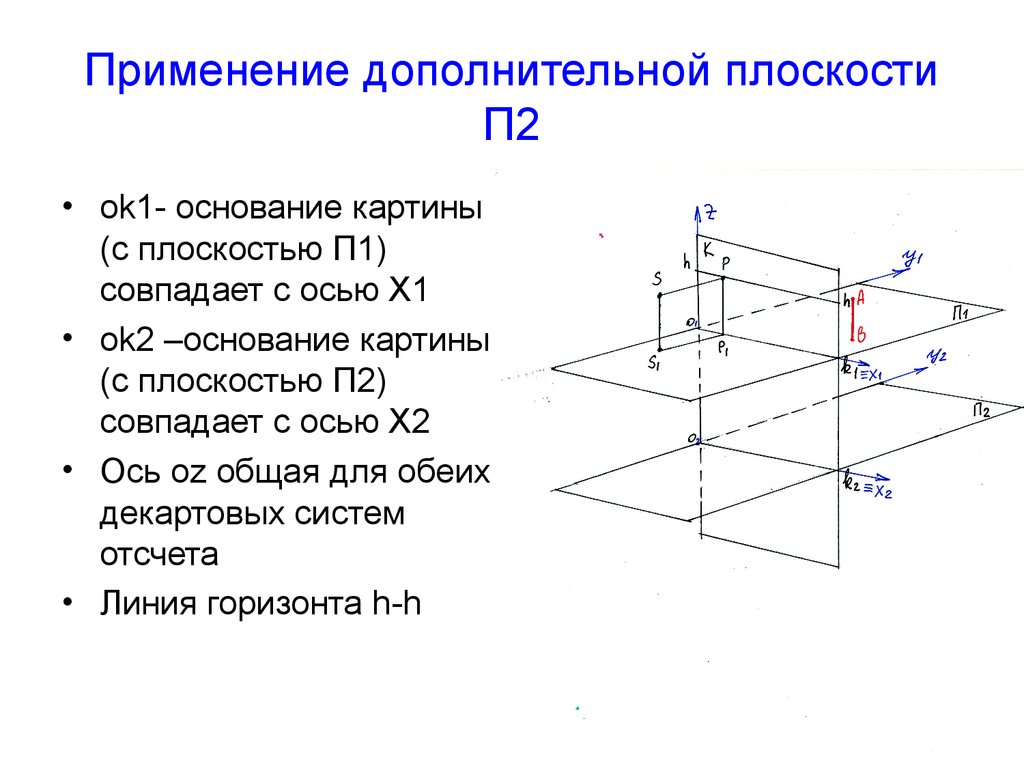
4. Применение дополнительной плоскости П2

• оk1- основание картины
(с плоскостью П1)
совпадает с осью Х1
• ok2 –основание картины
(с плоскостью П2)
совпадает с осью Х2
• Ось оz общая для обеих
декартовых систем
отсчета
• Линия горизонта h-h

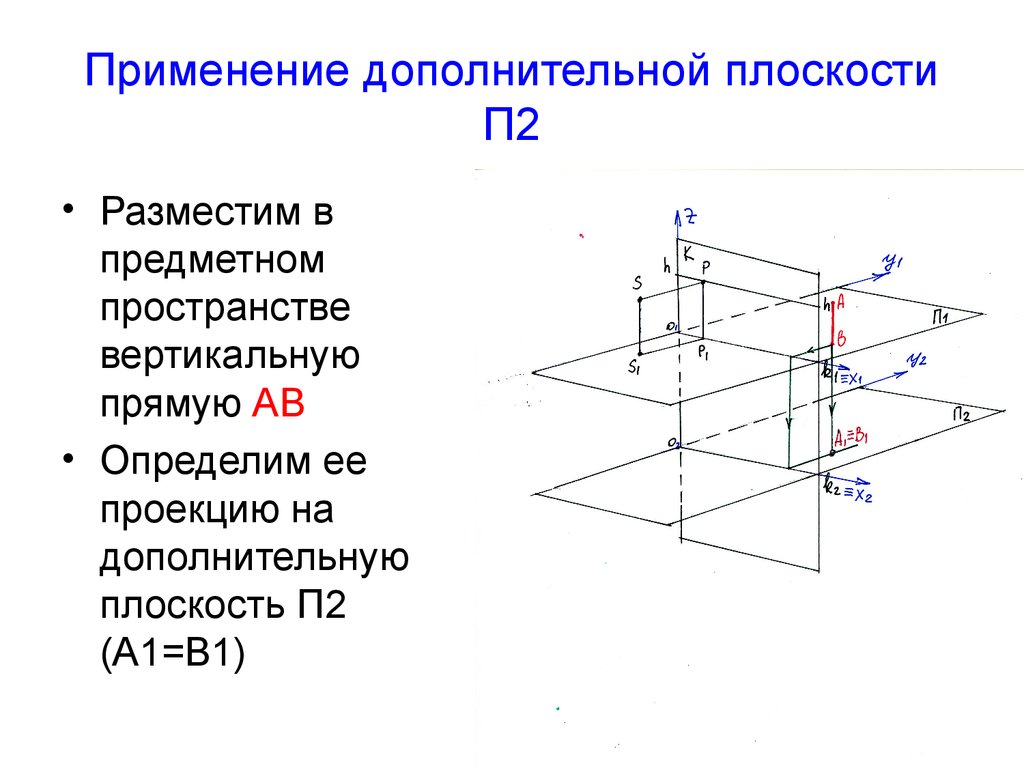
5. Применение дополнительной плоскости П2

• Разместим в
предметном
пространстве
вертикальную
прямую АВ
• Определим ее
проекцию на
дополнительную
плоскость П2
(А1=В1)

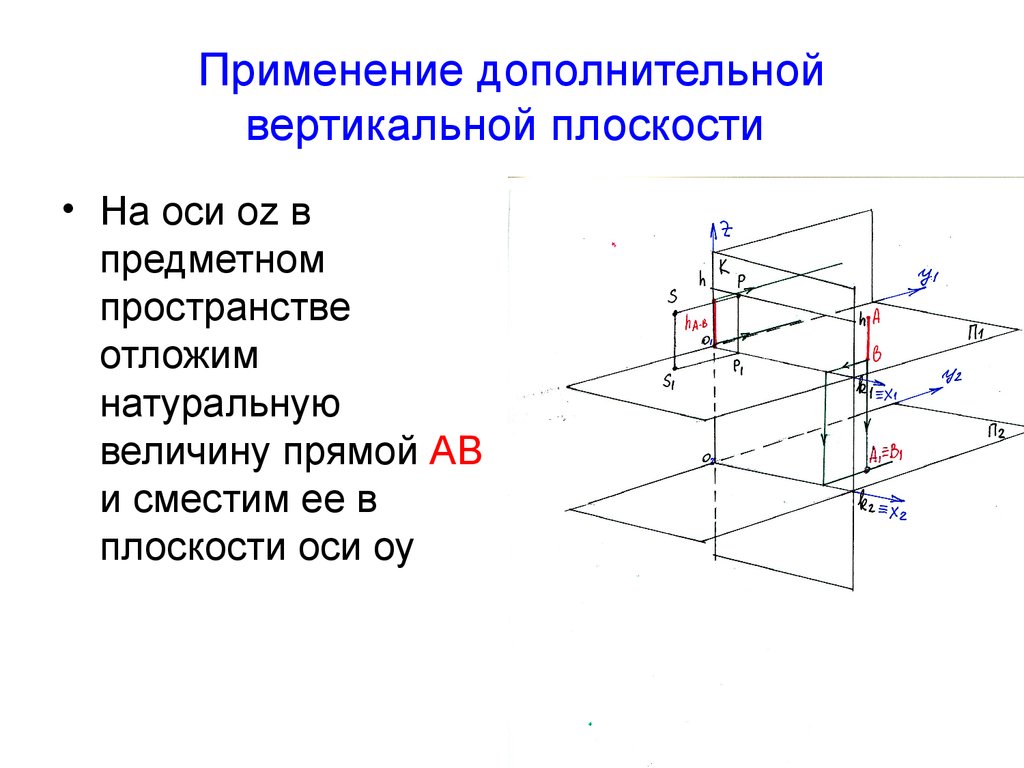
6. Применение дополнительной вертикальной плоскости

• На оси oz в
предметном
пространстве
отложим
натуральную
величину прямой АВ
и сместим ее в
плоскости оси оу

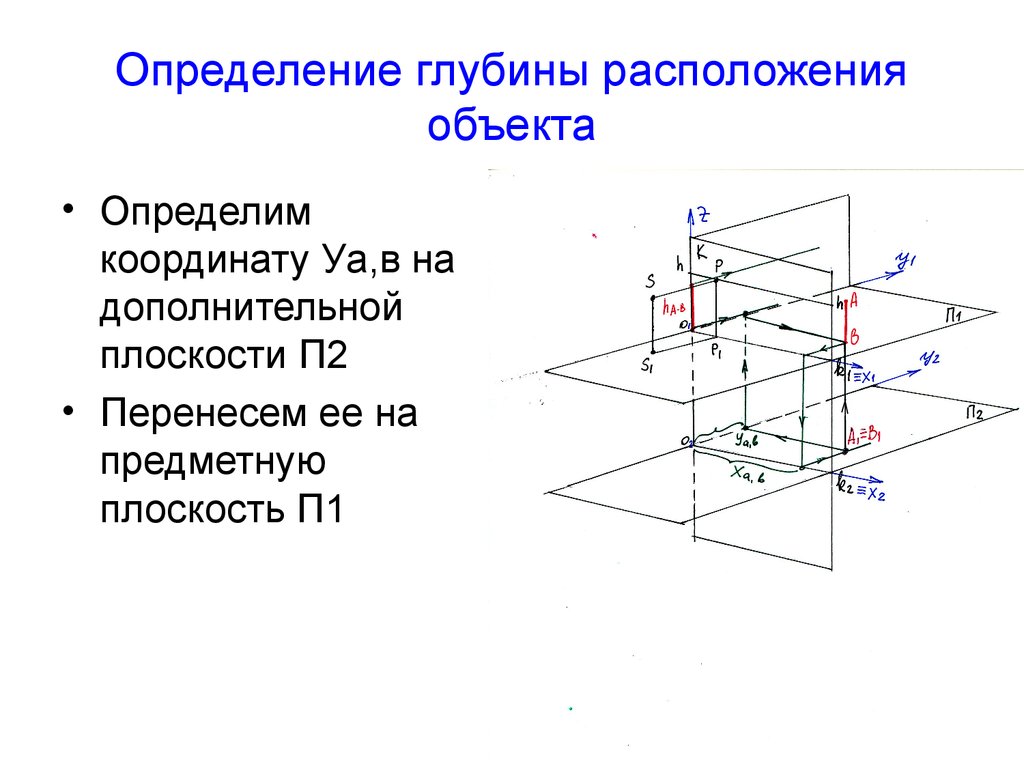
7. Определение глубины расположения объекта

• Определим
координату Уа,в на
дополнительной
плоскости П2
• Перенесем ее на
предметную
плоскость П1

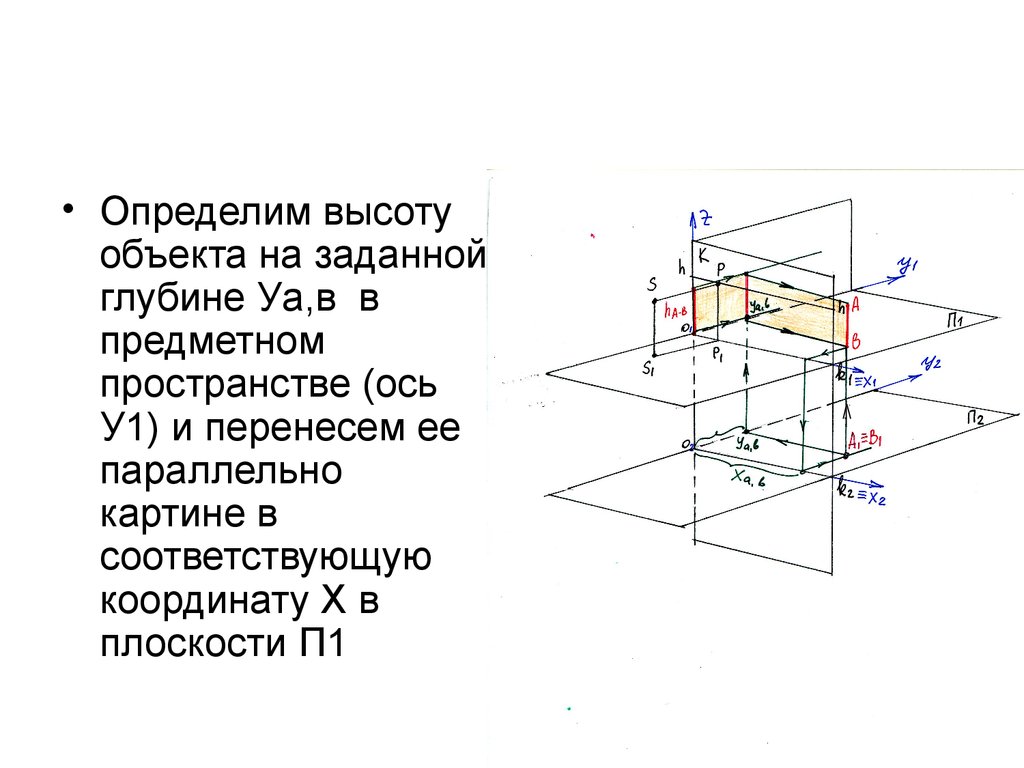
8.

• Определим высоту
объекта на заданной
глубине Уа,в в
предметном
пространстве (ось
У1) и перенесем ее
параллельно
картине в
соответствующую
координату Х в
плоскости П1

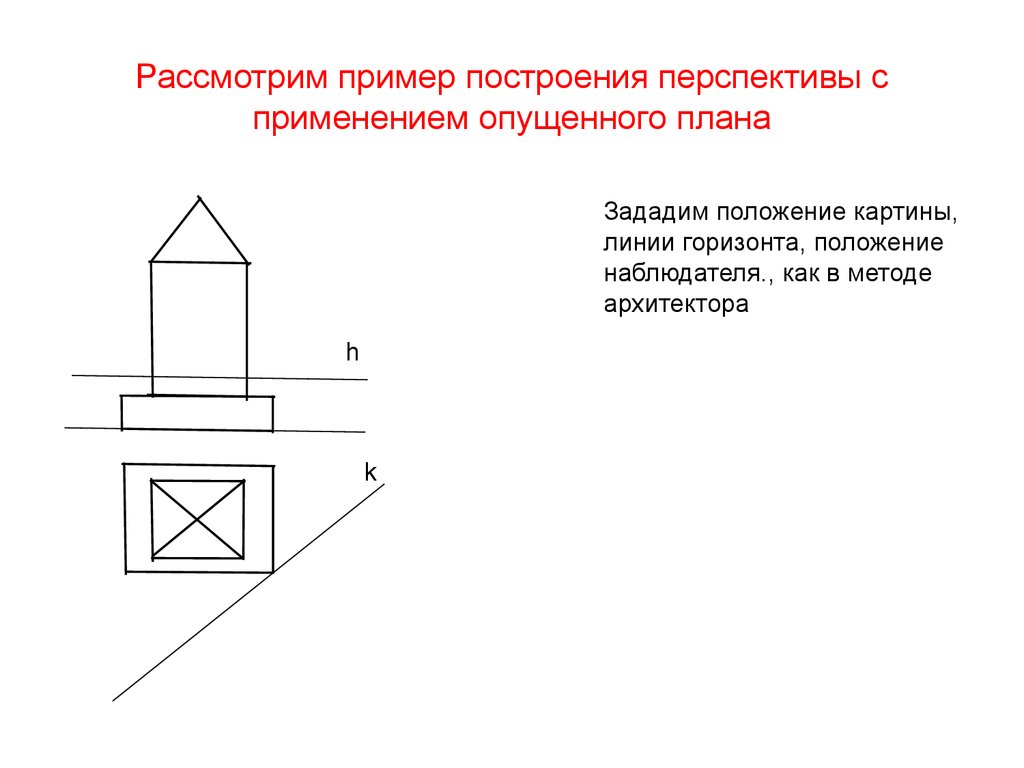
9. Рассмотрим пример построения перспективы с применением опущенного плана

Зададим положение картины,
линии горизонта, положение
наблюдателя., как в методе
архитектора
h
k

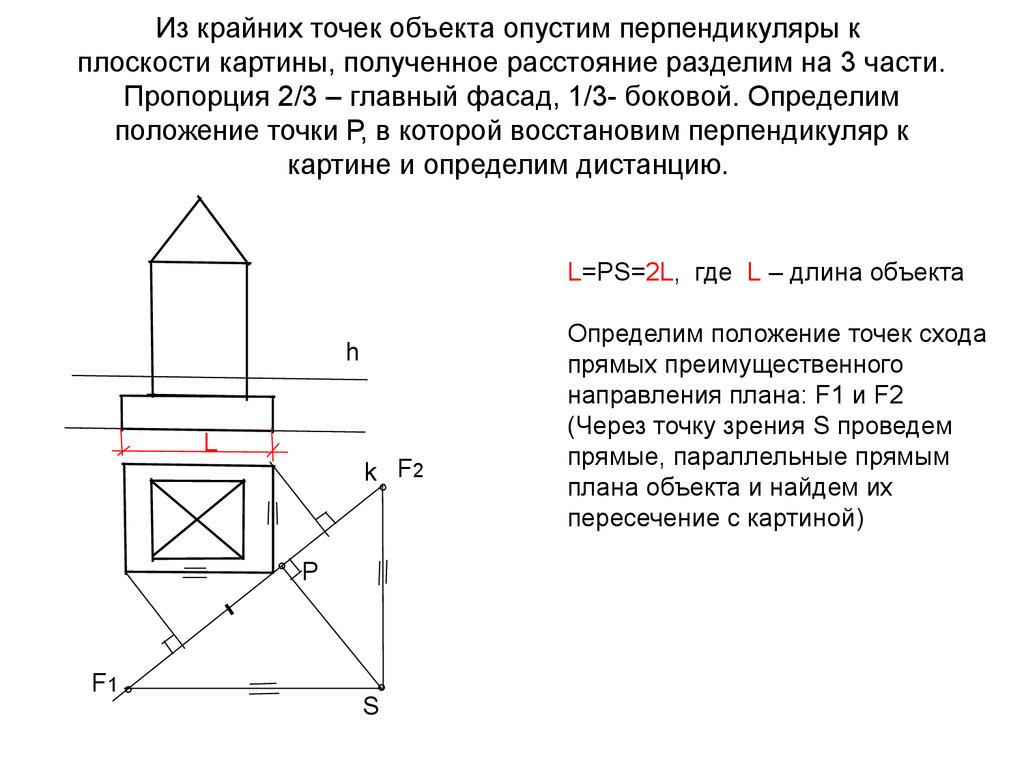
10. Из крайних точек объекта опустим перпендикуляры к плоскости картины, полученное расстояние разделим на 3 части. Пропорция 2/3 –

главный фасад, 1/3- боковой. Определим
положение точки Р, в которой восстановим перпендикуляр к
картине и определим дистанцию.
L=РS=2L, где L – длина объекта
h
L
k F2
°
° Р
F1
°
S°
Определим положение точек схода
прямых преимущественного
направления плана: F1 и F2
(Через точку зрения S проведем
прямые, параллельные прямым
плана объекта и найдем их
пересечение с картиной)

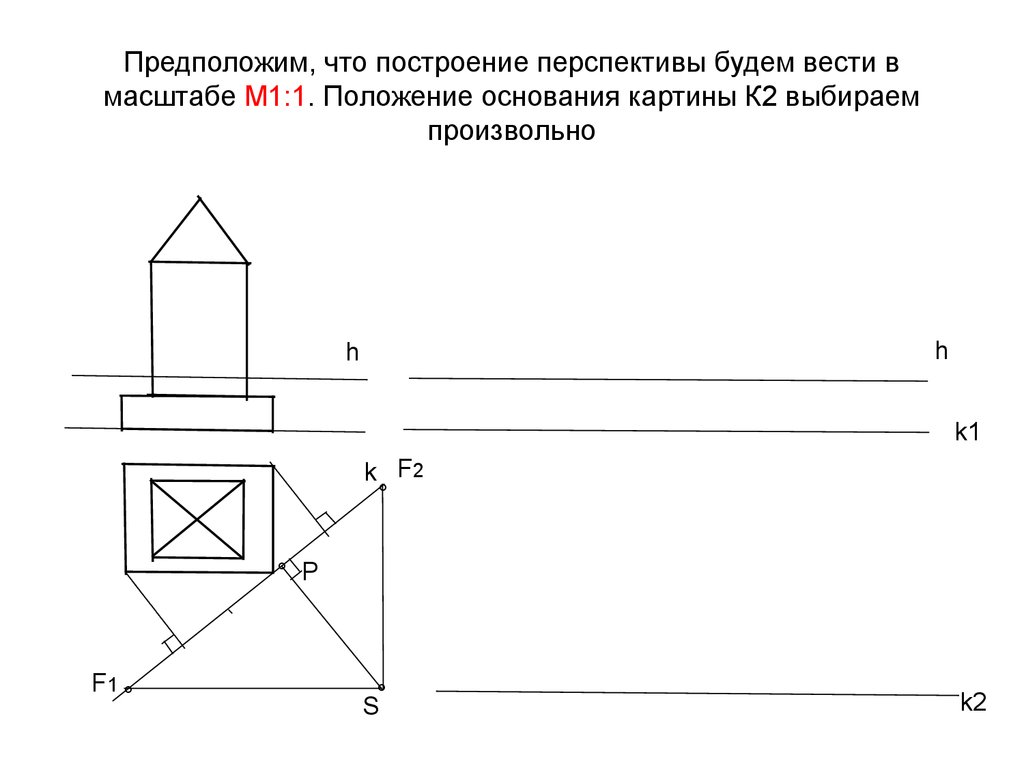
11. Предположим, что построение перспективы будем вести в масштабе М1:1. Положение основания картины К2 выбираем произвольно

h
h
k1
k F2
°
° Р
F1
°
S°
k2

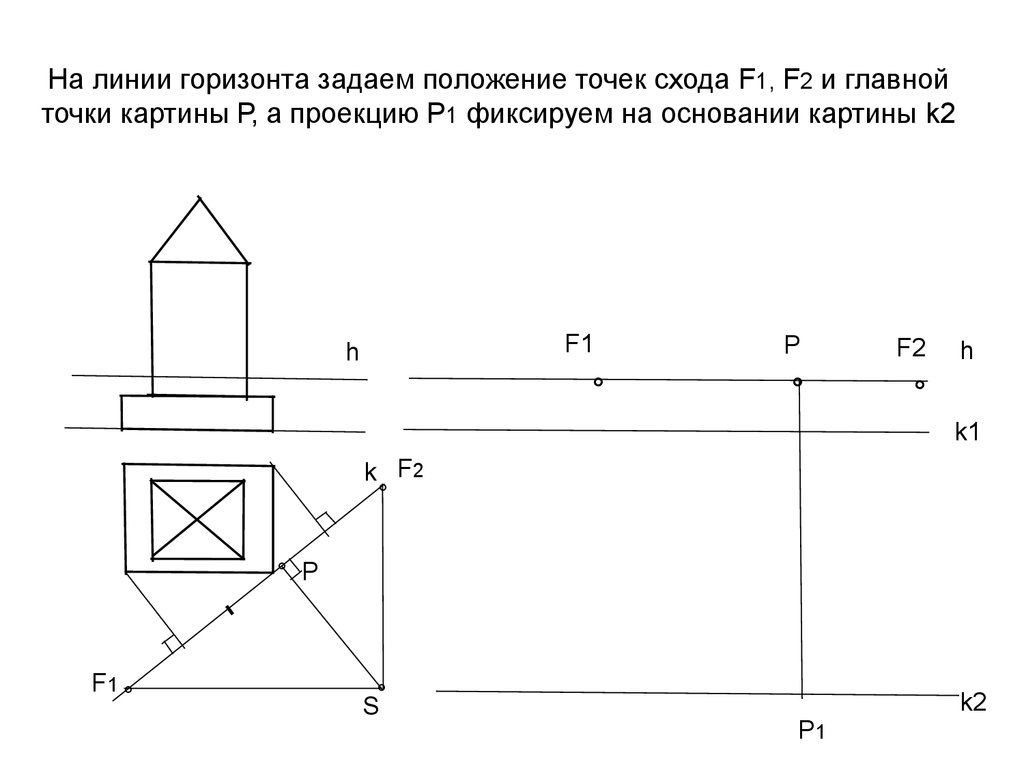
12. На линии горизонта задаем положение точек схода F1, F2 и главной точки картины Р, а проекцию Р1 фиксируем на основании картины

k2
F1
h
°
Р
F2
°
°
h
k1
k F2
°
° Р
F1
°
S°
Р1
k2

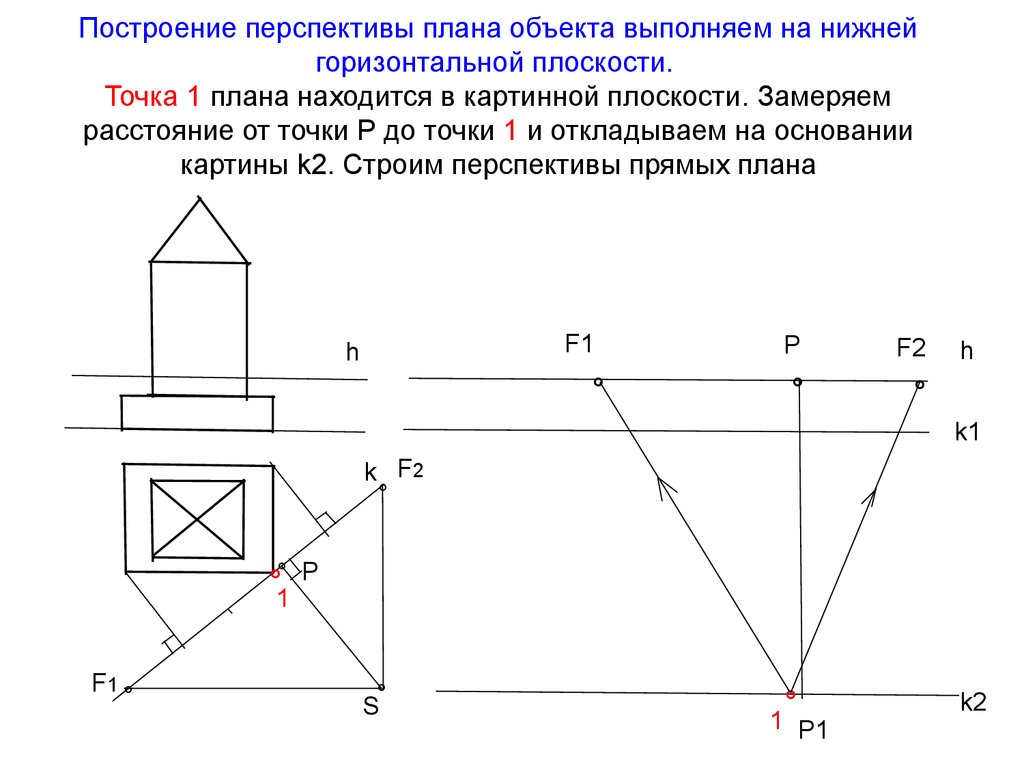
13. Построение перспективы плана объекта выполняем на нижней горизонтальной плоскости. Точка 1 плана находится в картинной

плоскости. Замеряем
расстояние от точки Р до точки 1 и откладываем на основании
картины k2. Строим перспективы прямых плана
F1
h
°
Р
F2
°
°
h
k1
k F2
°
°° Р
1
F1
°
S°
°
1 Р1
k2

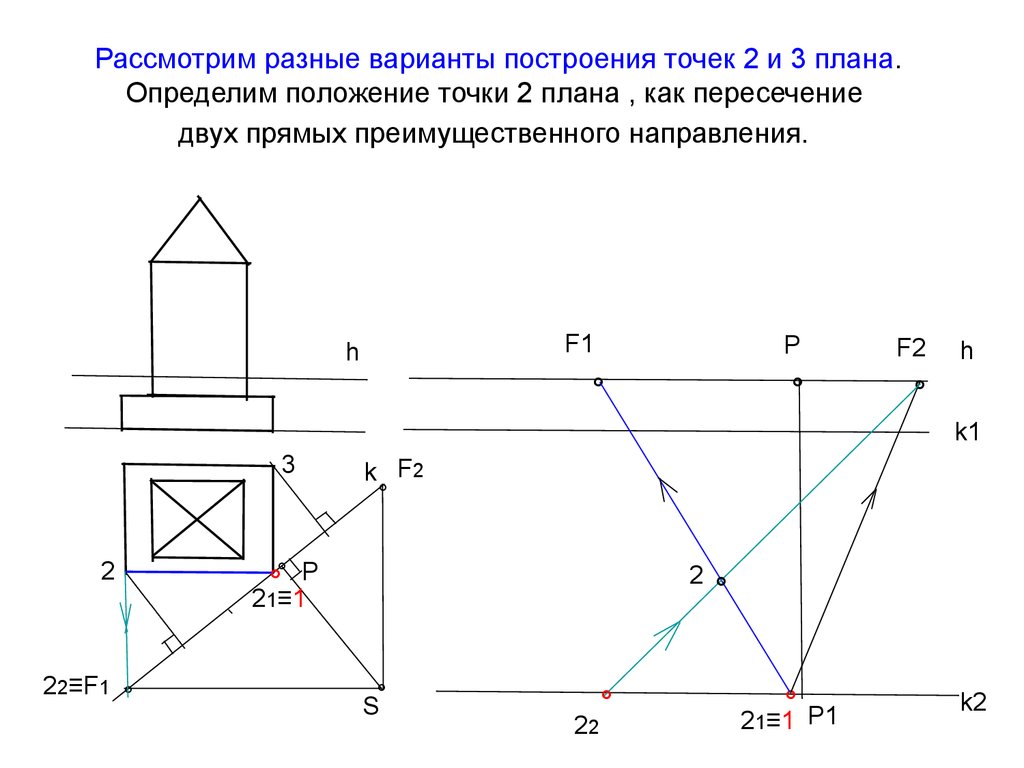
14. Рассмотрим разные варианты построения точек 2 и 3 плана. Определим положение точки 2 плана , как пересечение двух прямых

преимущественного направления.
F1
h
°
Р
F2
°
°
h
k1
3
2
22≡F1 °
k F2
°
°° Р
2
21≡1
S°
22
°
°
° Р1
21≡1
k2

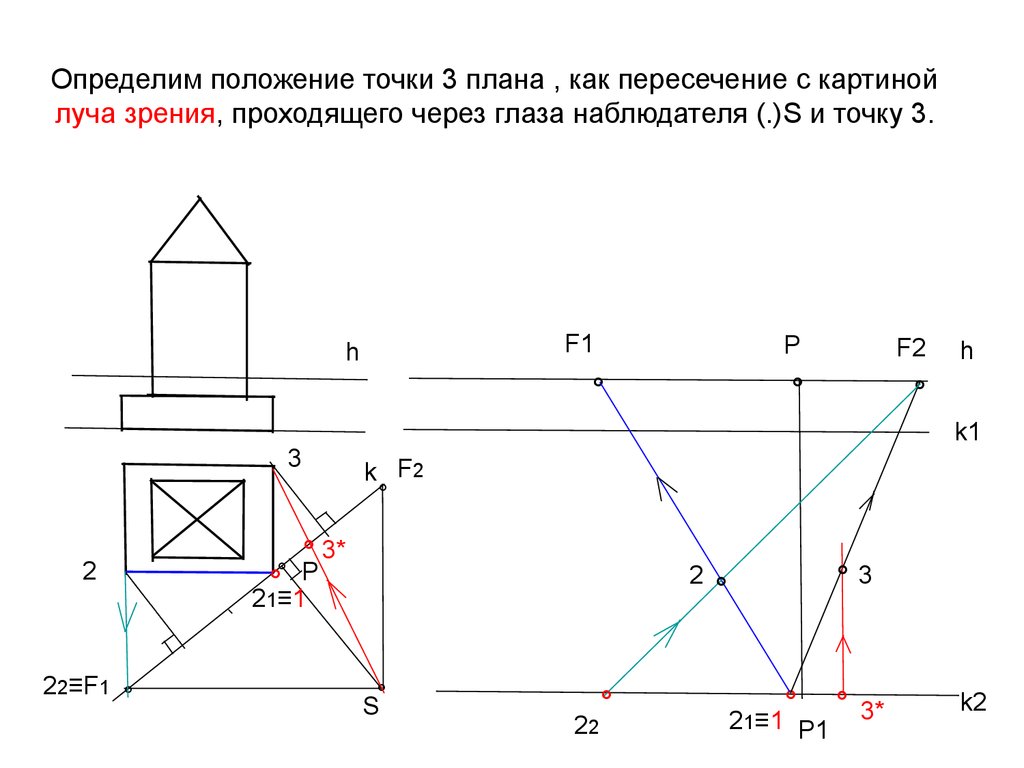
15. Определим положение точки 3 плана , как пересечение с картиной луча зрения, проходящего через глаза наблюдателя (.)S и точку 3.

F1
h
°
22≡F1 °
F2
°
°
h
k1
3
2
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
°
°3
°
°
21≡1 Р1
° 3*
k2

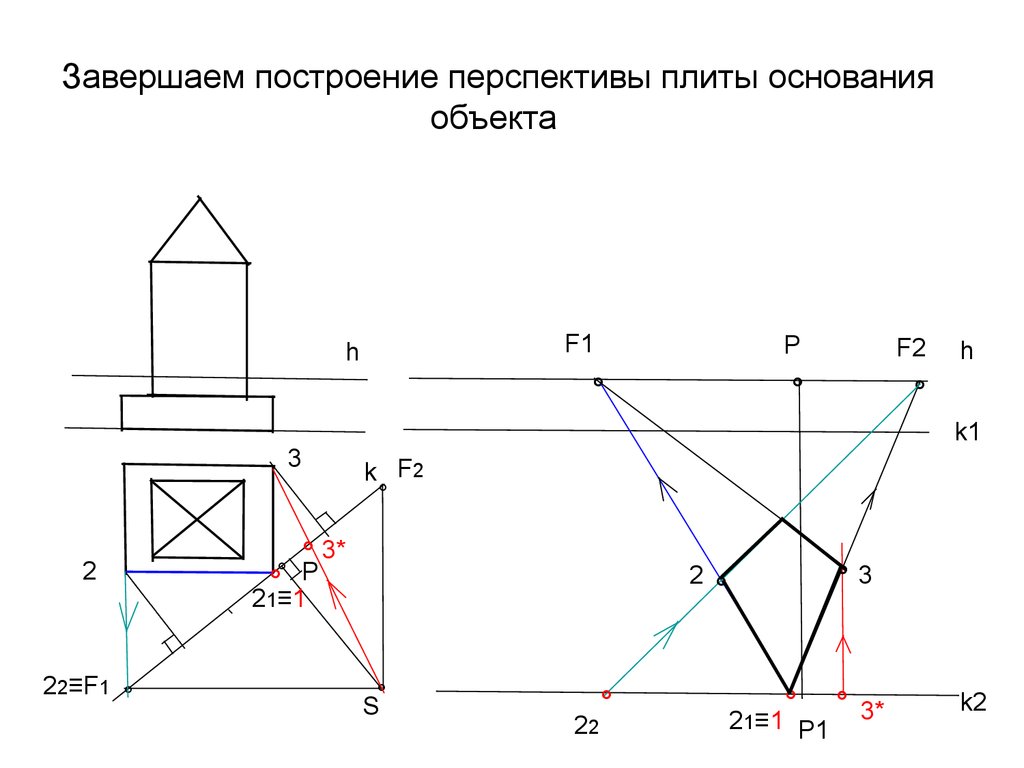
16. Завершаем построение перспективы плиты основания объекта

F1
h
°
22≡F1 °
F2
°
°
h
k1
3
2
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
°
°3
°
°
21≡1 Р1
° 3*
k2

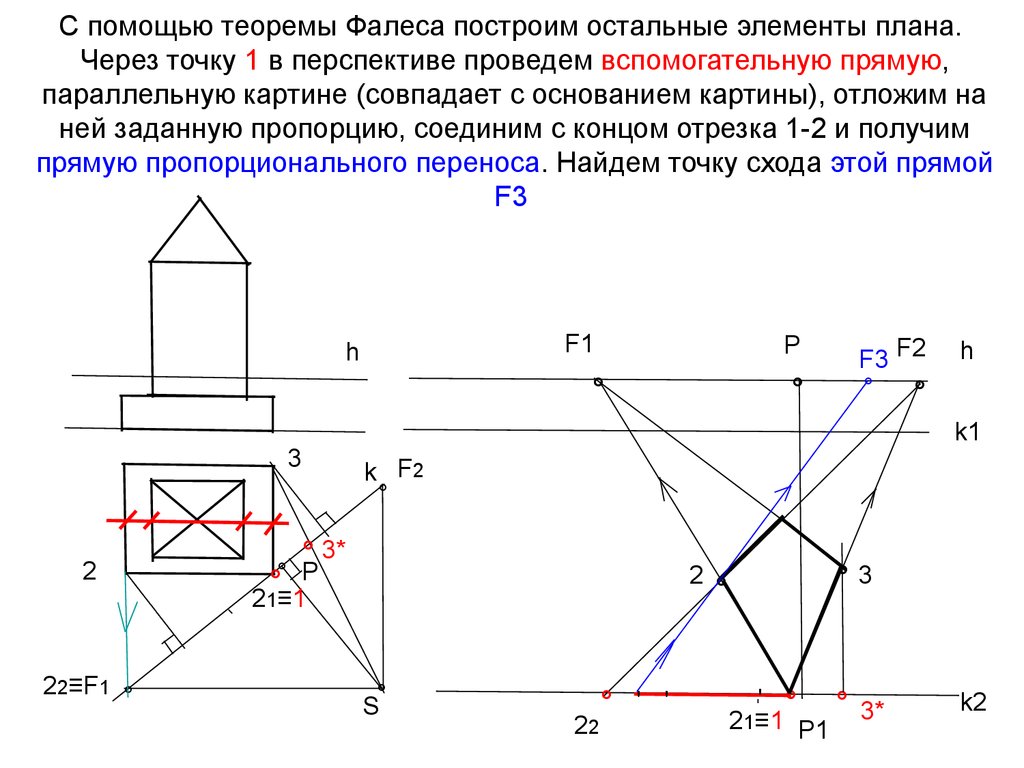
17. С помощью теоремы Фалеса построим остальные элементы плана. Через точку 1 в перспективе проведем вспомогательную прямую,

параллельную картине (совпадает с основанием картины), отложим на
ней заданную пропорцию, соединим с концом отрезка 1-2 и получим
прямую пропорционального переноса. Найдем точку схода этой прямой
F3
F1
h
Р
°
22≡F1 °
h
k1
3
2
°
F3 F2
°
°
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' °
°
21≡1 Р1 3*
k2

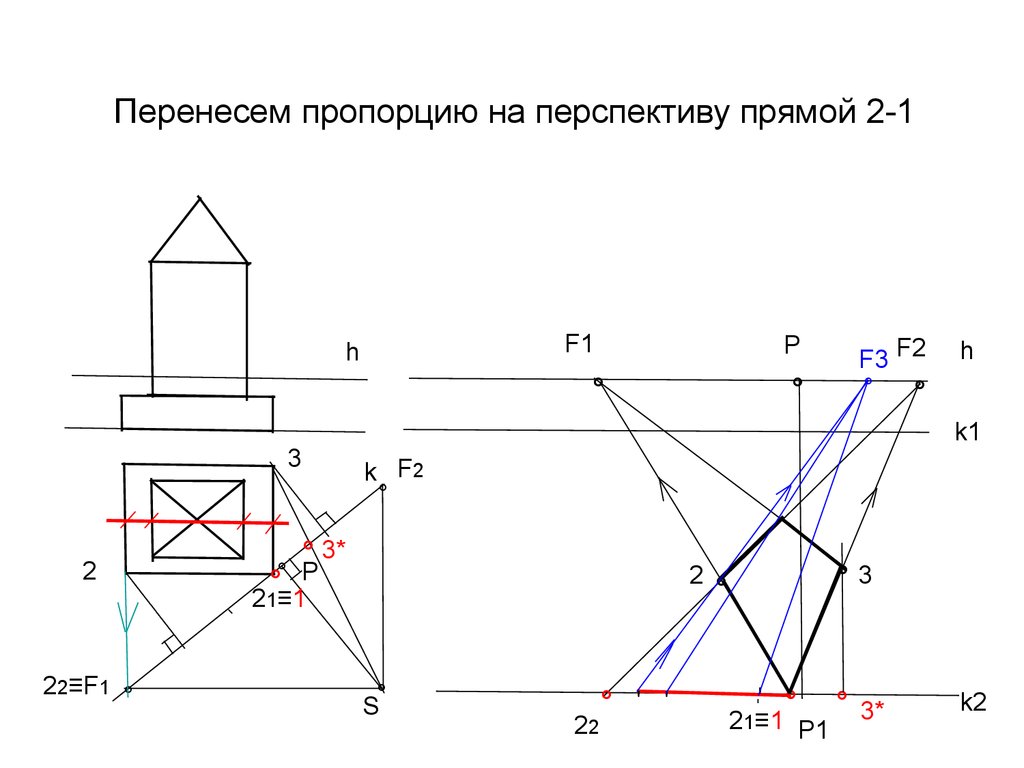
18. Перенесем пропорцию на перспективу прямой 2-1

F1
h
Р
°
22≡F1 °
h
k1
3
2
°
F3 F2
°
°
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' °
°
21≡1 Р1 3*
k2

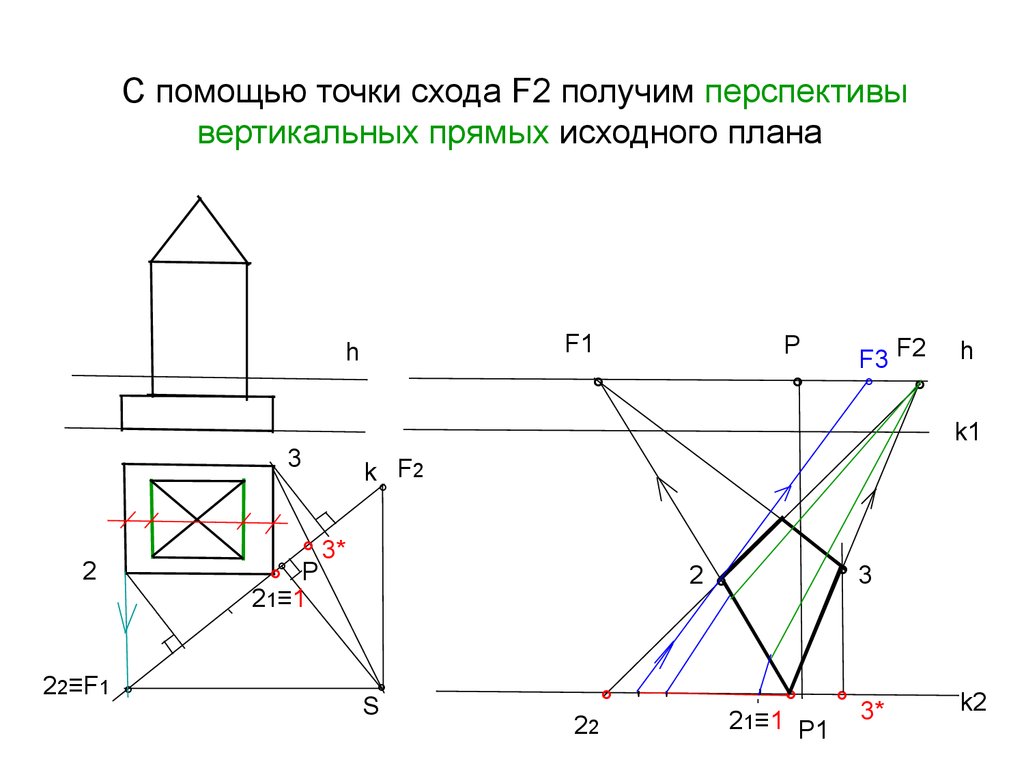
19. С помощью точки схода F2 получим перспективы вертикальных прямых исходного плана

F1
h
Р
°
22≡F1 °
h
k1
3
2
°
F3 F2
°
°
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' °
°
21≡1 Р1 3*
k2

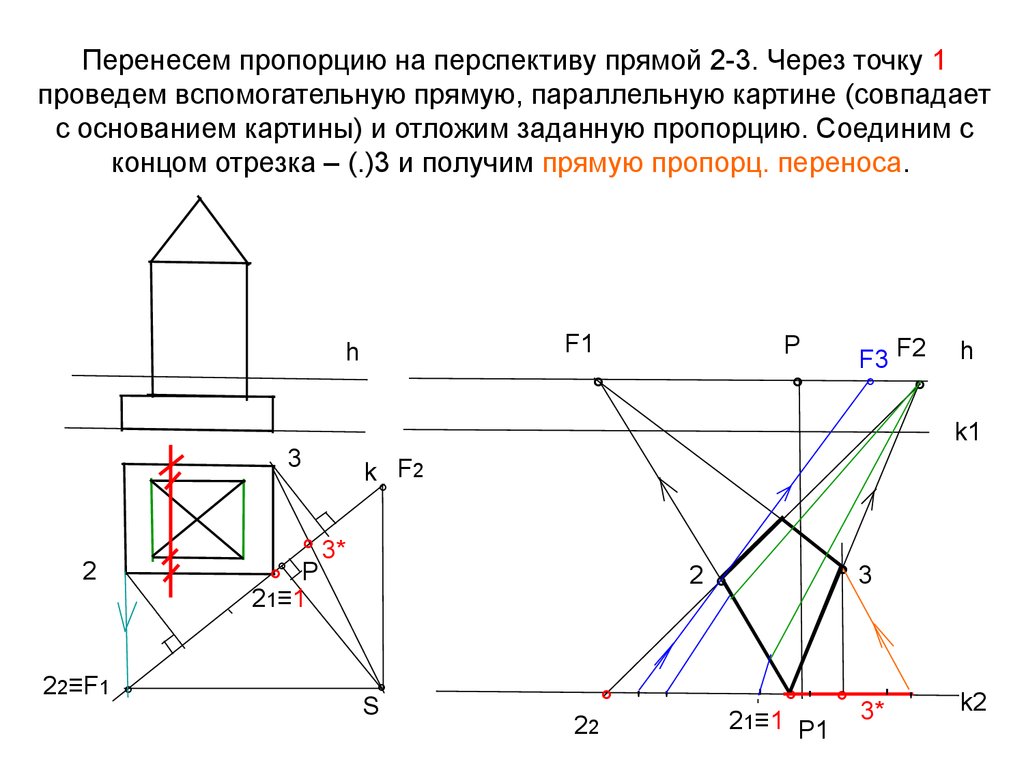
20. Перенесем пропорцию на перспективу прямой 2-3. Через точку 1 проведем вспомогательную прямую, параллельную картине (совпадает с

основанием картины) и отложим заданную пропорцию. Соединим с
концом отрезка – (.)3 и получим прямую пропорц. переноса.
F1
h
Р
°
22≡F1 °
h
k1
3
2
°
F3 F2
° °
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

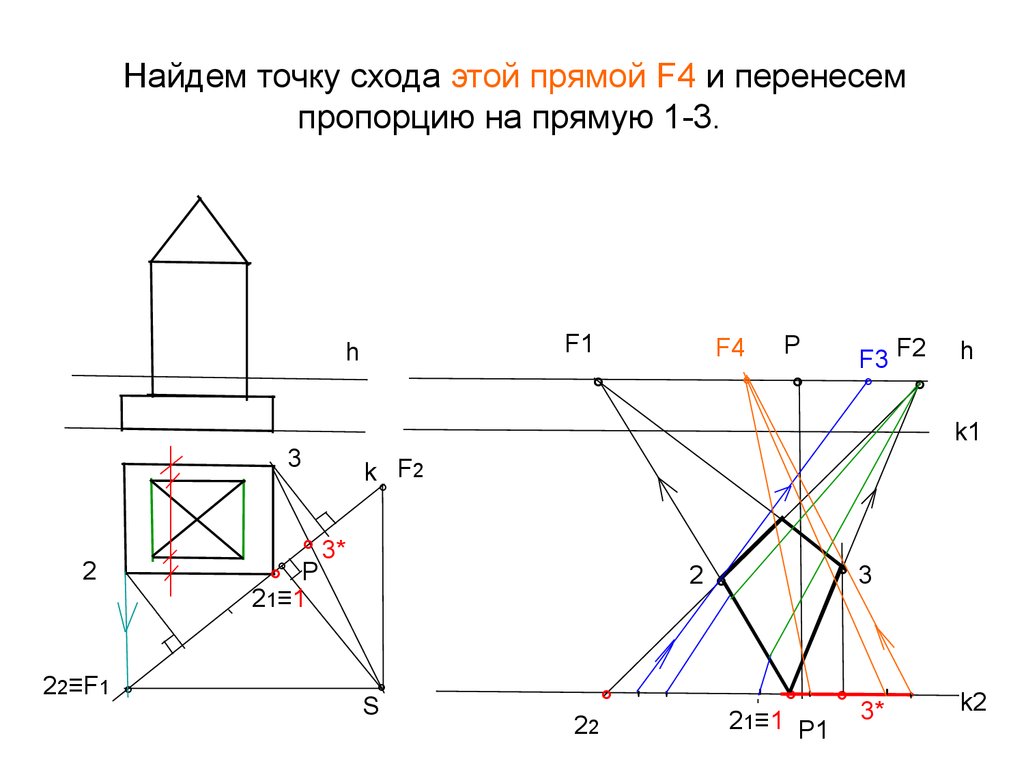
21. Найдем точку схода этой прямой F4 и перенесем пропорцию на прямую 1-3.

F1
h
F4
Р
°
°
°
22≡F1 °
h
k1
3
2
F3 F2
°
°
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

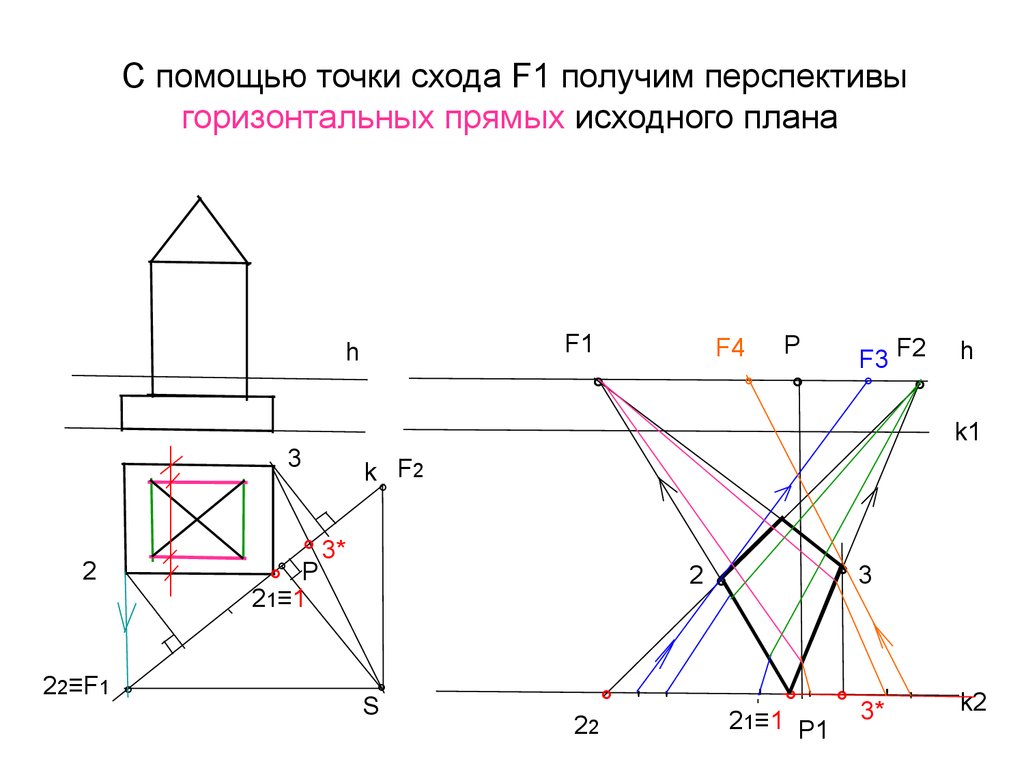
22. С помощью точки схода F1 получим перспективы горизонтальных прямых исходного плана

F1
h
F4
°
22≡F1 °
°
F3 F2
°
°
h
k1
3
2
°
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

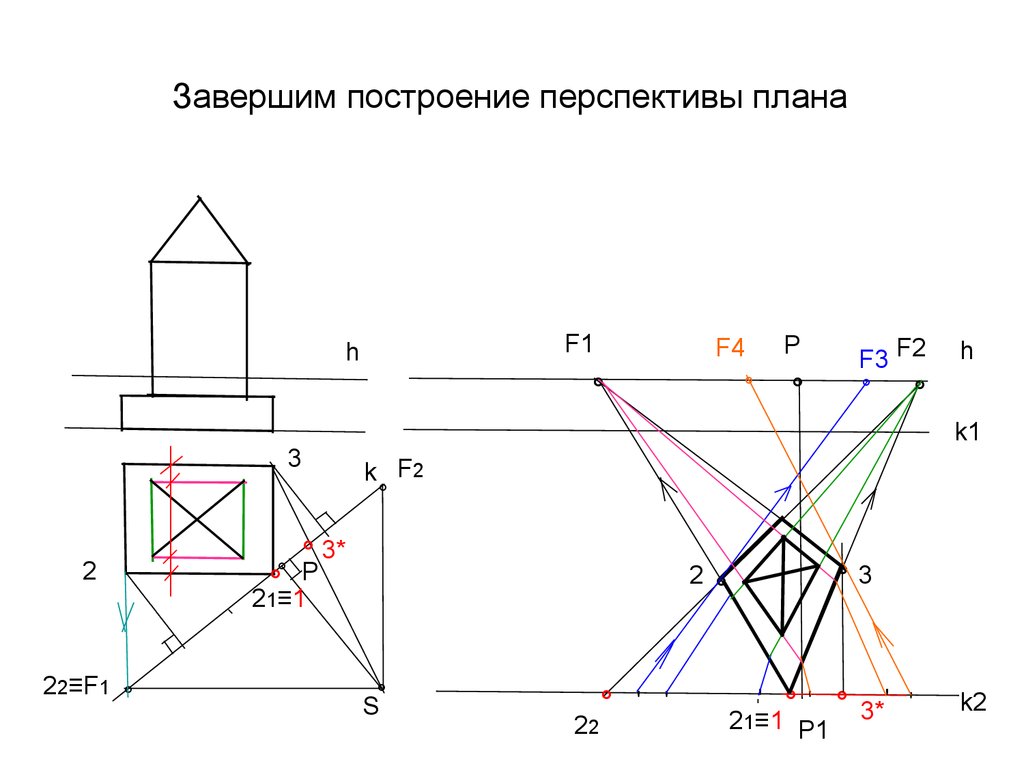
23. Завершим построение перспективы плана

F1
h
F4
°
22≡F1 °
°
F3 F2
°
°
h
k1
3
2
°
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

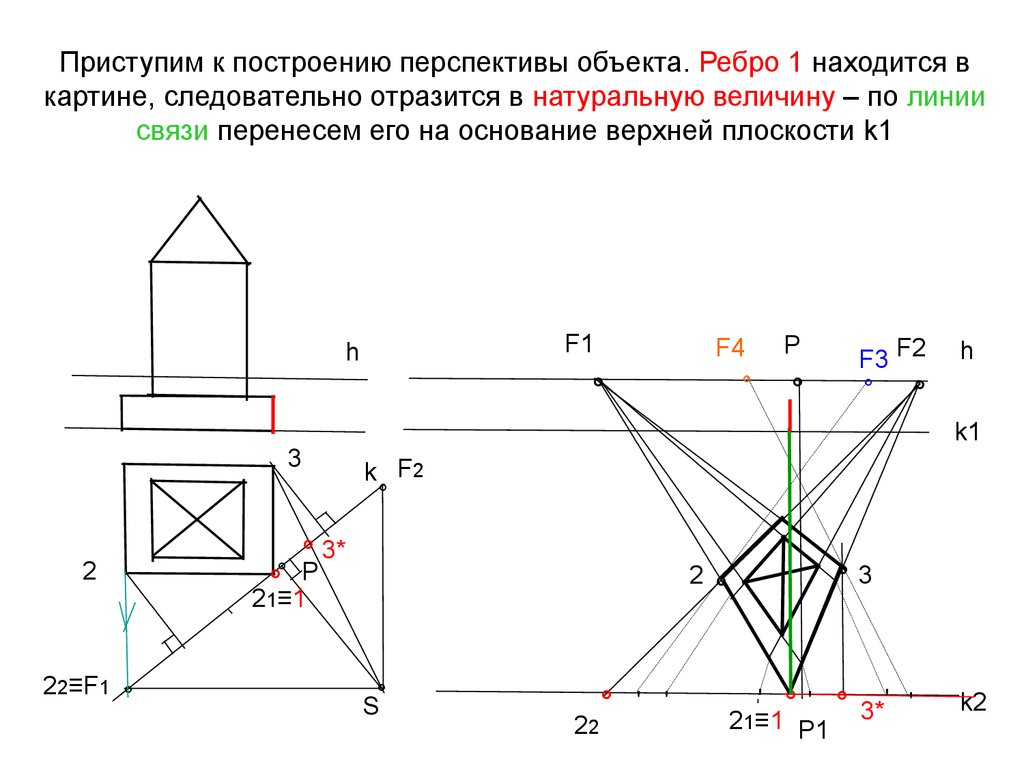
24. Приступим к построению перспективы объекта. Ребро 1 находится в картине, следовательно отразится в натуральную величину – по

линии
связи перенесем его на основание верхней плоскости k1
F1
h
F4
°
°
22≡F1 °
°
F3 F2
°
°
h
k1
3
2
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

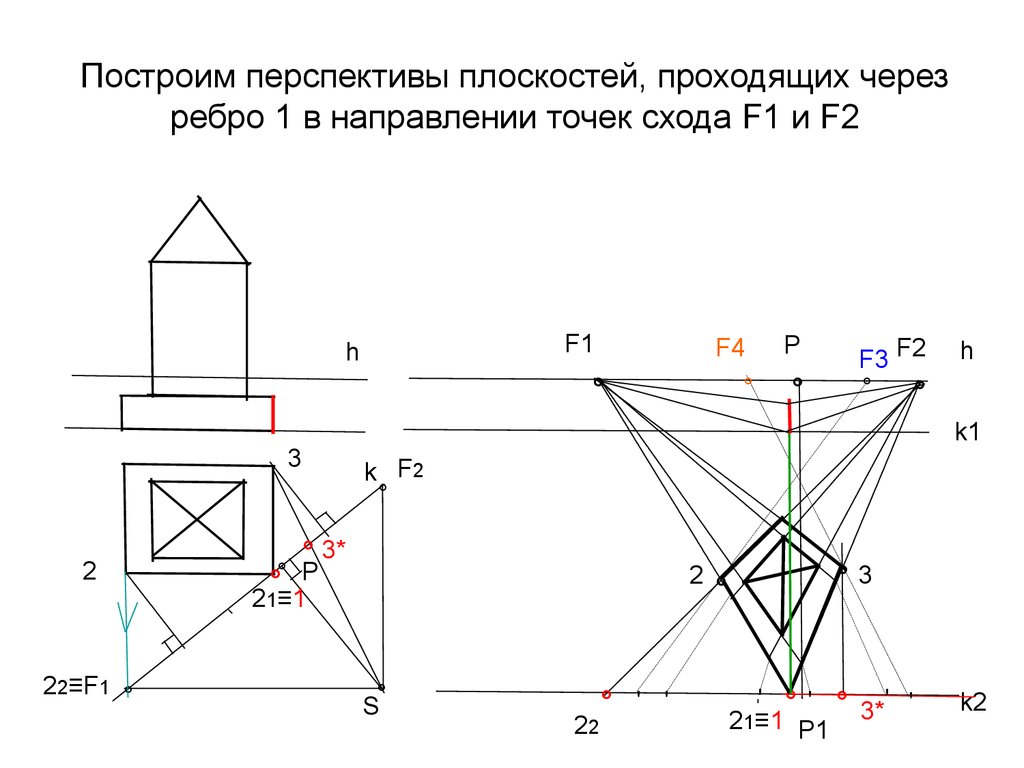
25. Построим перспективы плоскостей, проходящих через ребро 1 в направлении точек схода F1 и F2

F1
h
F4
°
22≡F1 °
°
F3 F2
°
°
h
k1
3
2
°
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

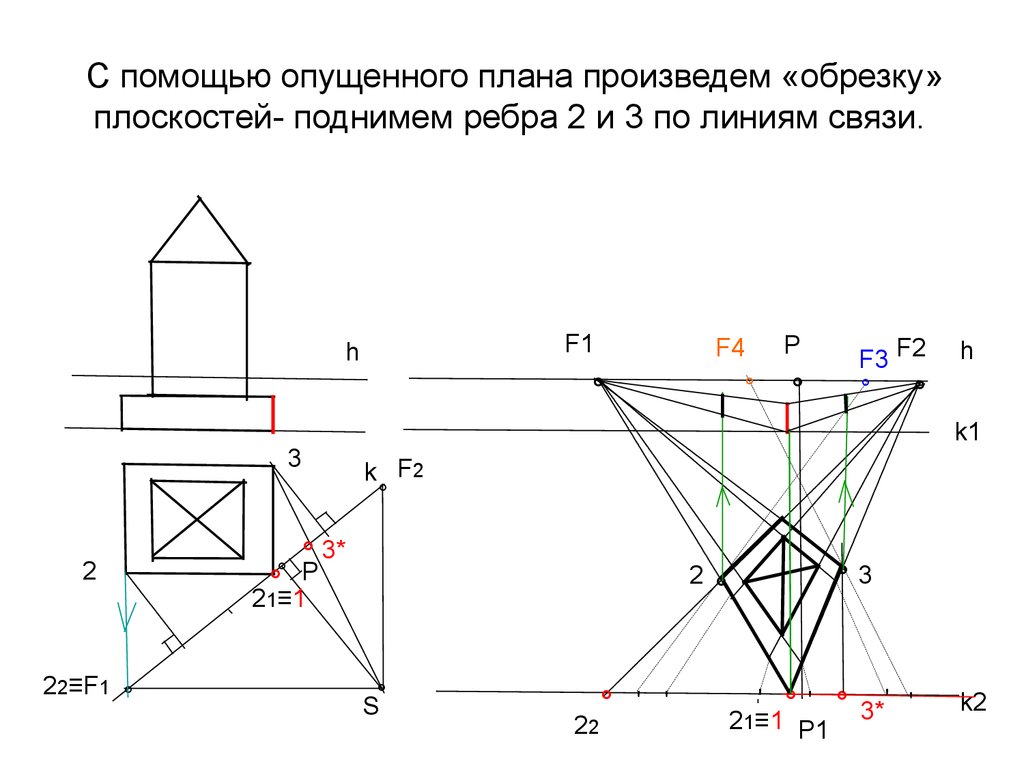
26. С помощью опущенного плана произведем «обрезку» плоскостей- поднимем ребра 2 и 3 по линиям связи.

F1
h
F4
°
22≡F1 °
°
F3 F2
°
°
h
k1
3
2
°
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

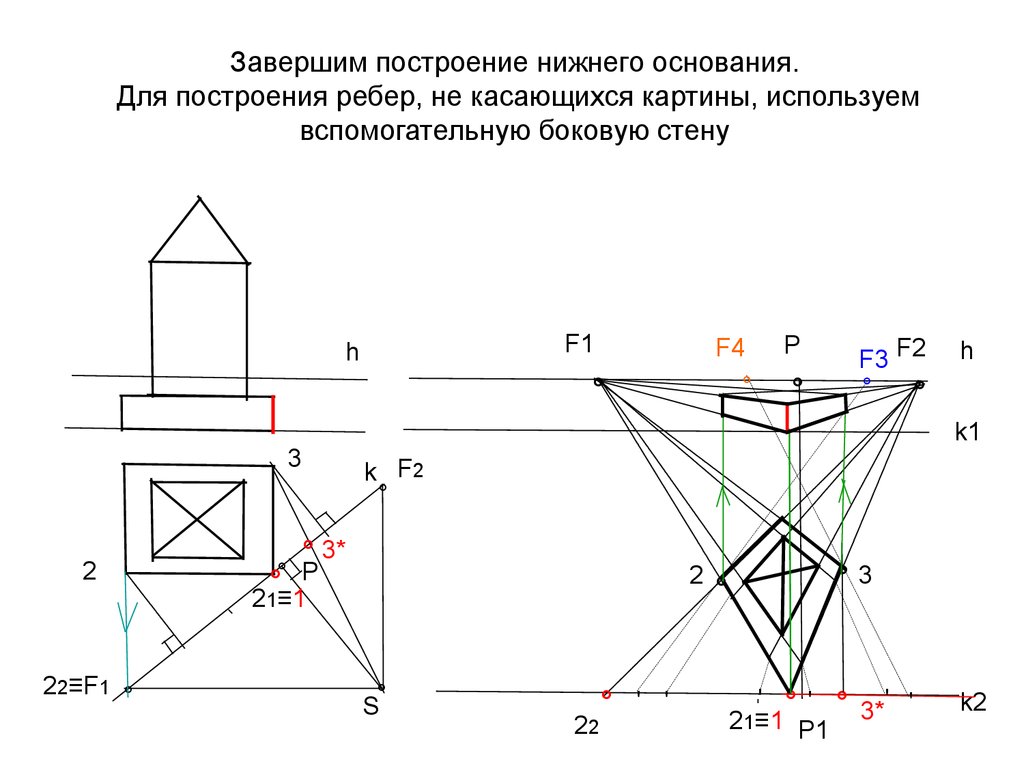
27. Завершим построение нижнего основания. Для построения ребер, не касающихся картины, используем вспомогательную боковую стену

F1
h
F4
°
°
22≡F1 °
°
F3 F2
°
°
h
k1
3
2
Р
k F2
°
° 3*
°° Р
2
21≡1
S°
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

28. Применение вспомогательной вертикальной плоскости (боковой стены)

• Боковая стена выбирается произвольно
• Картинным следом этой плоскости является
ось Оz, а точкой схода ее горизонталейпроизвольная точка на линии горизонта
• На оси Оz в предметном пространстве
откладывают истинные размеры ребер
объекта (от (.)О1) и определяют сокращение
высоты с помощью (.)схода горизонталей
плоскости

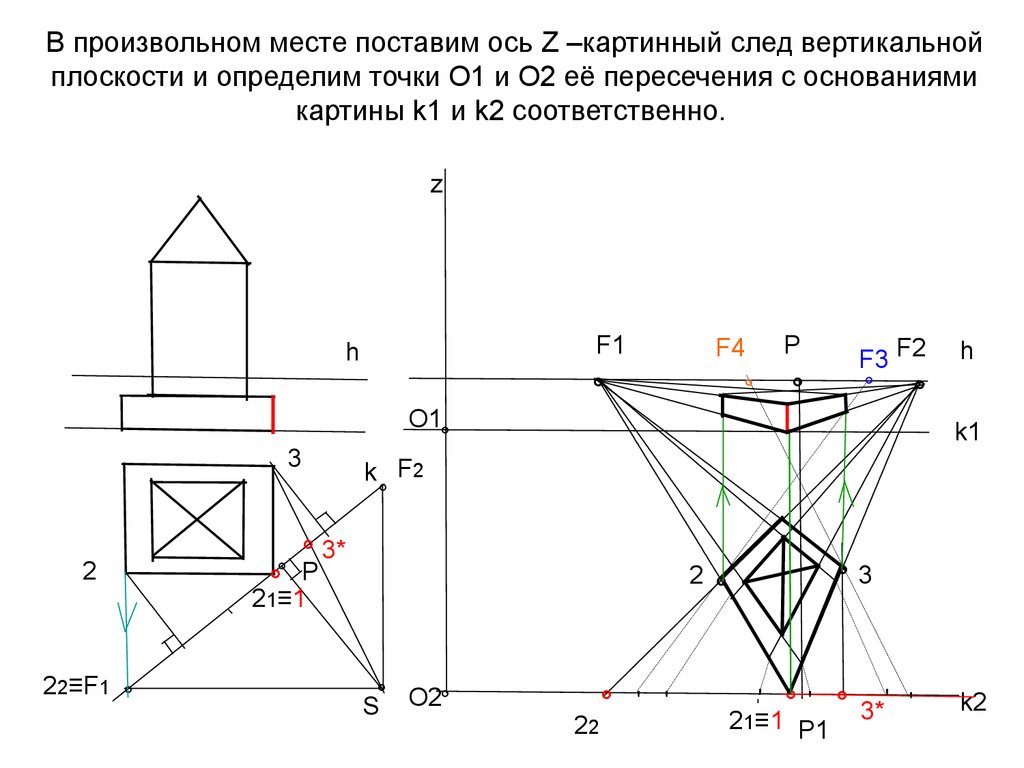
29. В произвольном месте поставим ось Z –картинный след вертикальной плоскости и определим точки О1 и О2 её пересечения с

основаниями
картины k1 и k2 соответственно.
z
F1
h
F4
°
О1
°
k F2
°
3
2
22≡F1 °
°
°
F3 F2
°
°
h
k1
° 3*
°° Р
2
21≡1
S° O2°
Р
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

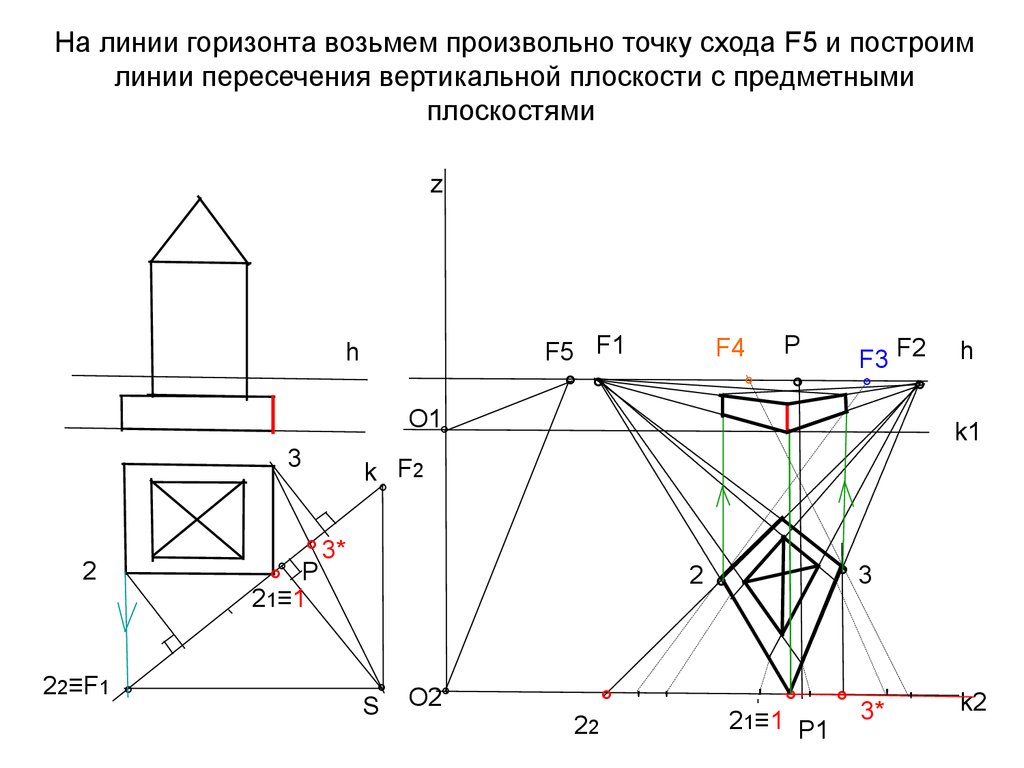
30. На линии горизонта возьмем произвольно точку схода F5 и построим линии пересечения вертикальной плоскости с предметными

плоскостями
z
F5 F1
h
F4
° °
О1
°
k F2
°
3
2
22≡F1 °
°
°
F3 F2
°
°
h
k1
° 3*
°° Р
2
21≡1
S° O2°
Р
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

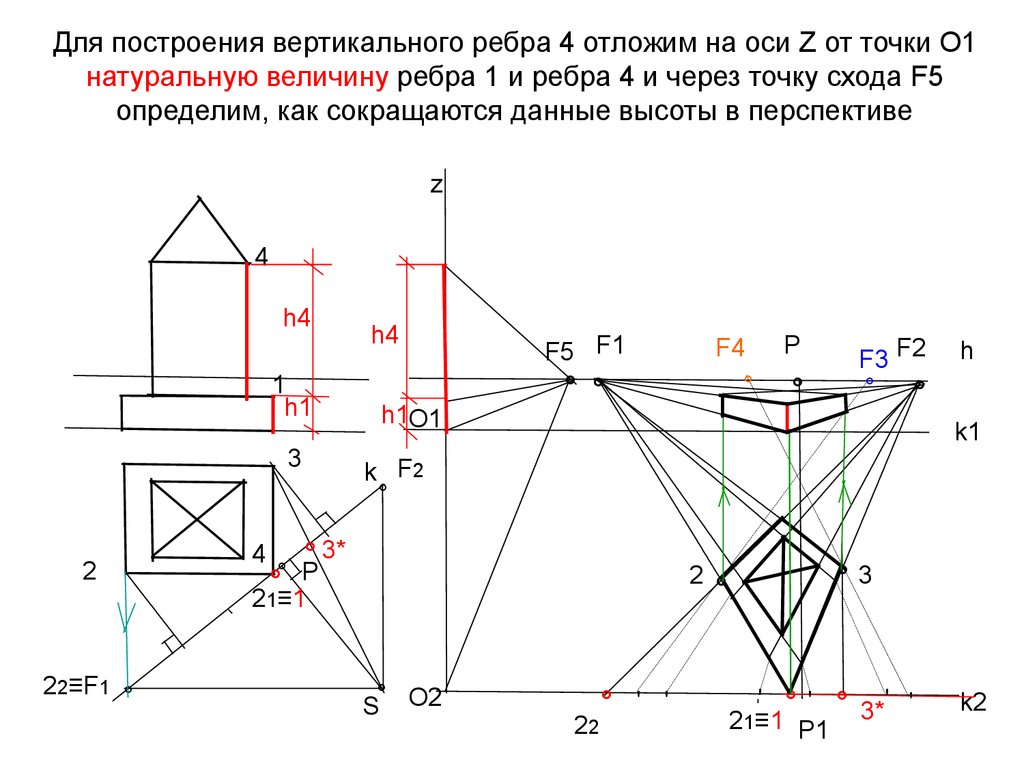
31. Для построения вертикального ребра 4 отложим на оси Z от точки О1 натуральную величину ребра 1 и ребра 4 и через точку схода F5

определим, как сокращаются данные высоты в перспективе
z
4
h4
1
h1
3
2
22≡F1 °
4
h4
h1О1
F5 F1
F4
°
° °
Р
°
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
S° O2
22
° ' '
°
°3
' ° ' ° 3*' '
21≡1 Р1
k2

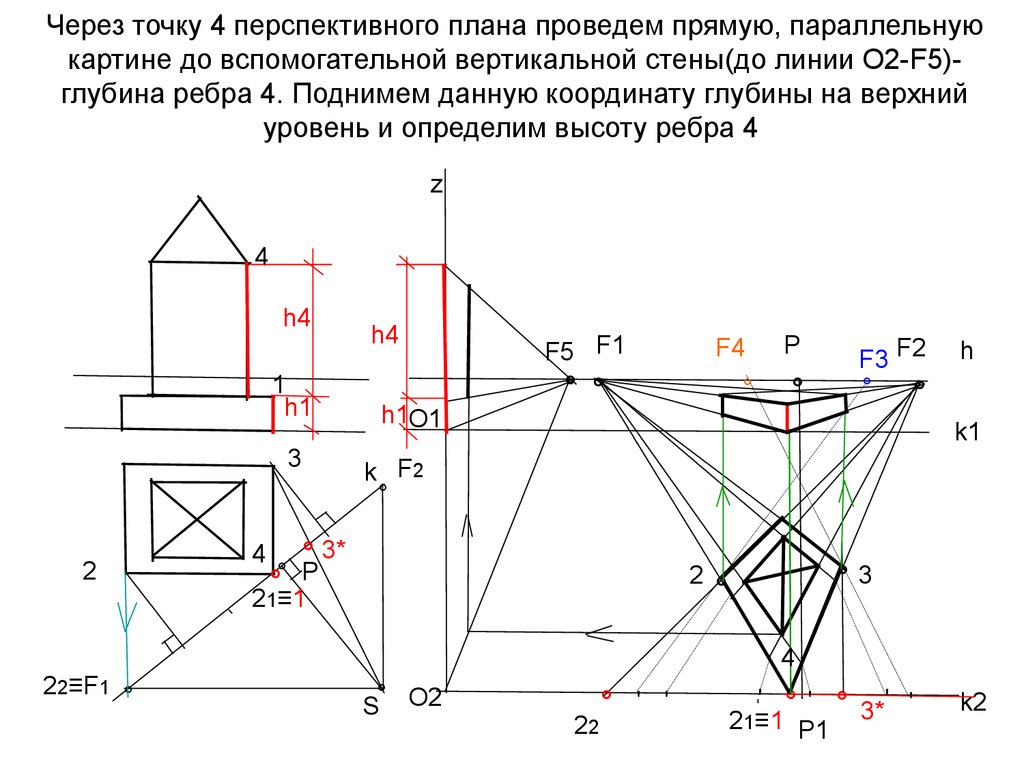
32. Через точку 4 перспективного плана проведем прямую, параллельную картине до вспомогательной вертикальной стены(до линии О2-F5)-

Через точку 4 перспективного плана проведем прямую, параллельную
картине до вспомогательной вертикальной стены(до линии О2-F5)глубина ребра 4. Поднимем данную координату глубины на верхний
уровень и определим высоту ребра 4
z
4
h4
1
h1
3
2
22≡F1 °
4
h4
h1О1
F5 F1
F4
° °
°
Р
°
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
°3
°
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

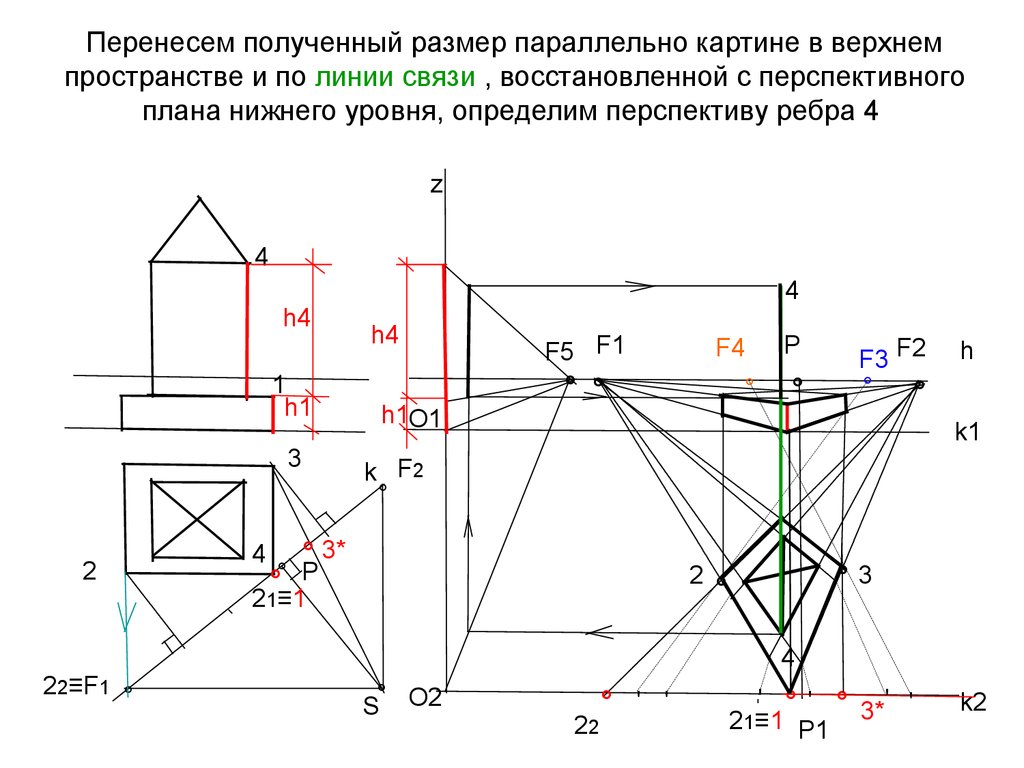
33. Перенесем полученный размер параллельно картине в верхнем пространстве и по линии связи , восстановленной с перспективного

плана нижнего уровня, определим перспективу ребра 4
z
4
h4
1
h1
3
2
22≡F1 °
4
4
h4
h1О1
F5 F1
F4
° °
°
Р
°
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
°3
°
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

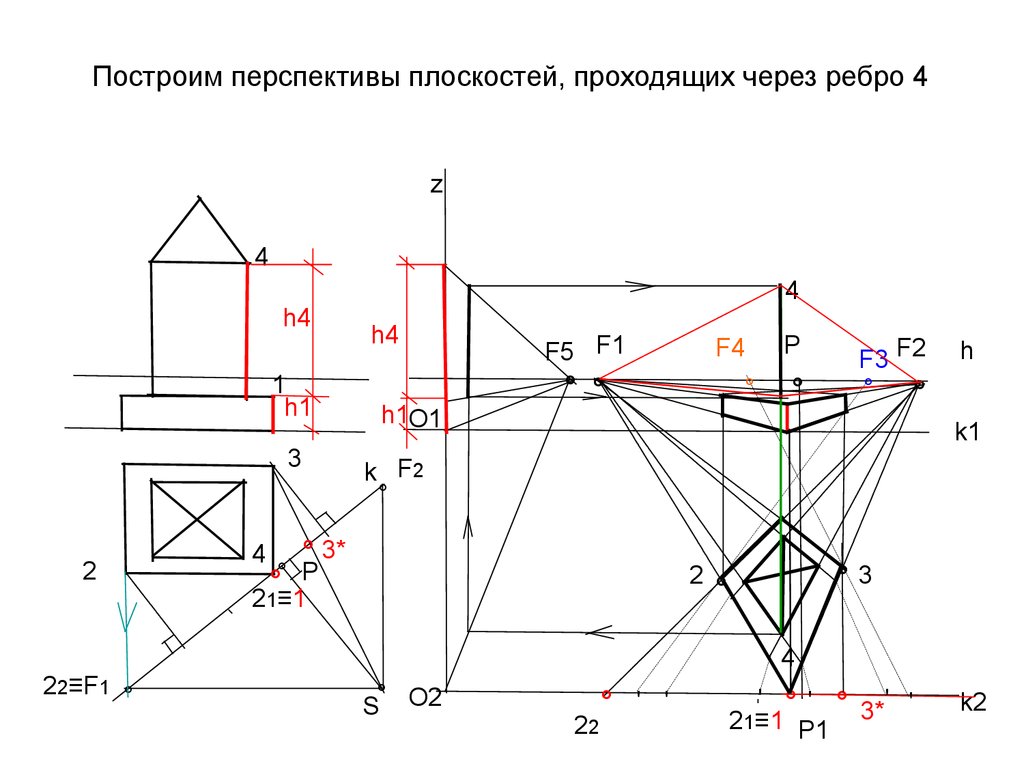
34. Построим перспективы плоскостей, проходящих через ребро 4

z
4
h4
1
h1
3
2
22≡F1 °
4
4
h4
h1О1
F5 F1
F4
° °
°
Р
°
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
°3
°
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

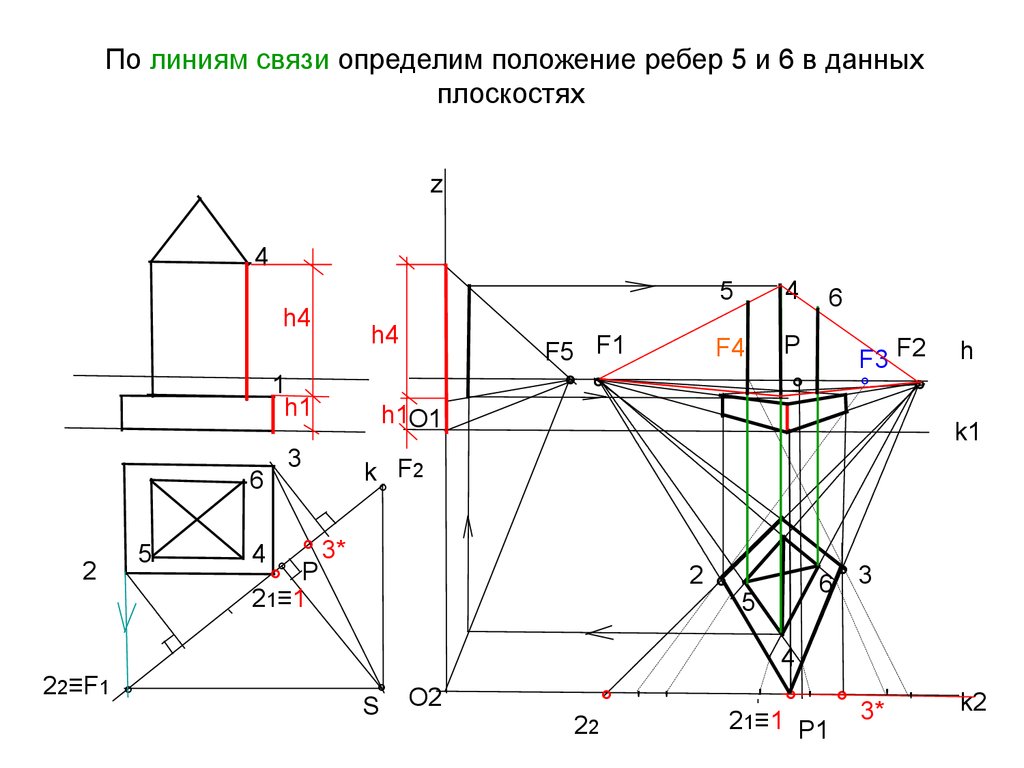
35. По линиям связи определим положение ребер 5 и 6 в данных плоскостях

z
4
h4
1
h1
6
2
22≡F1 °
5
4
3
h4
h1О1
F5 F1
5
4
F4
Р
° °
°
6
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
6° 3
° 5
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

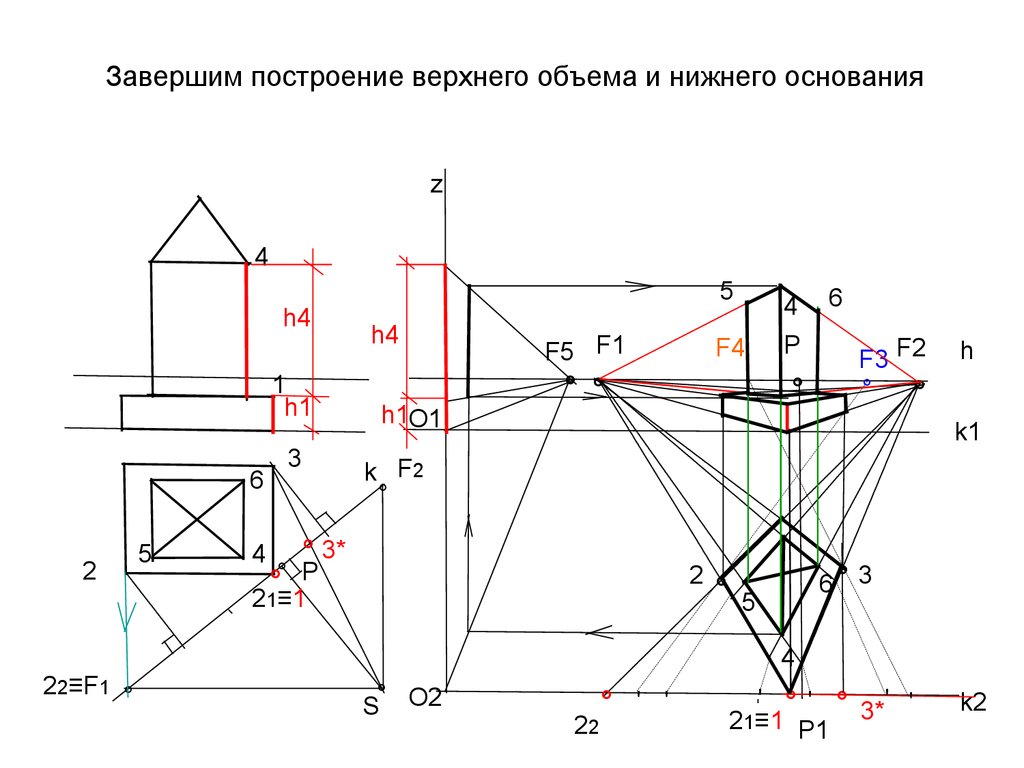
36. Завершим построение верхнего объема и нижнего основания

z
4
h4
1
h1
6
2
22≡F1 °
5
4
3
5
h4
h1О1
F5 F1
F4
° °
4
Р
°
6
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
6° 3
° 5
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

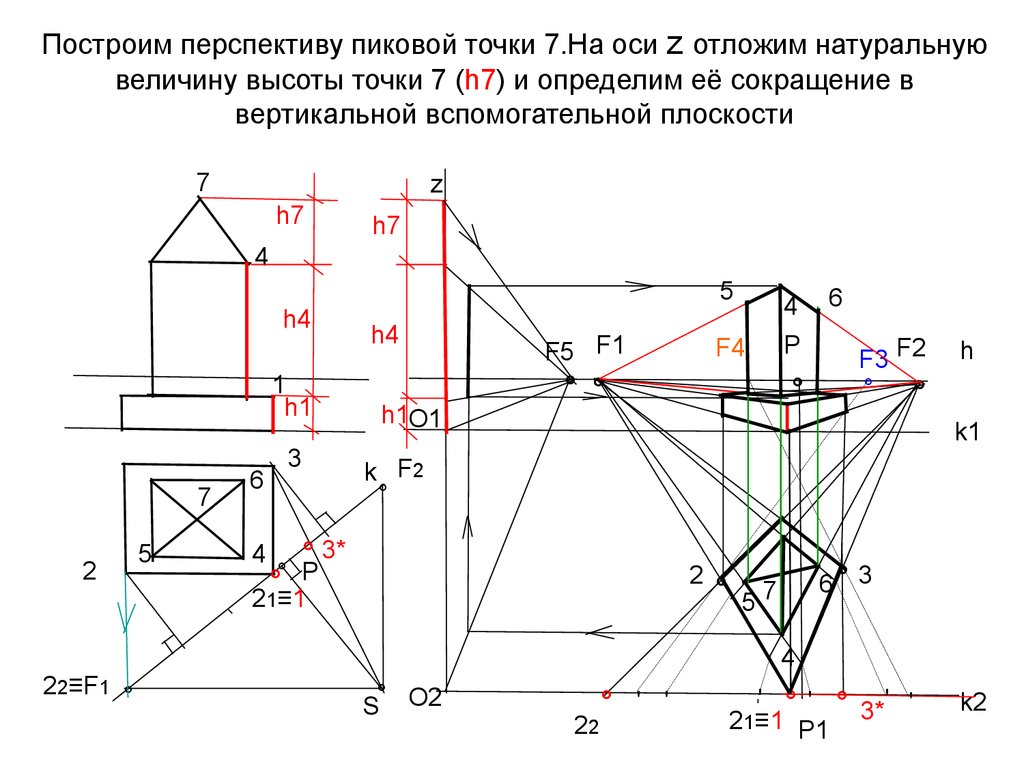
37. Построим перспективу пиковой точки 7.На оси z отложим натуральную величину высоты точки 7 (h7) и определим её сокращение в

вертикальной вспомогательной плоскости
7
z
h7
h7
4
h4
1
h1
7
2
22≡F1 °
5
6
4
3
5
h4
h1О1
F5 F1
F4
° °
4
Р
°
6
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
6° 3
° 57
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

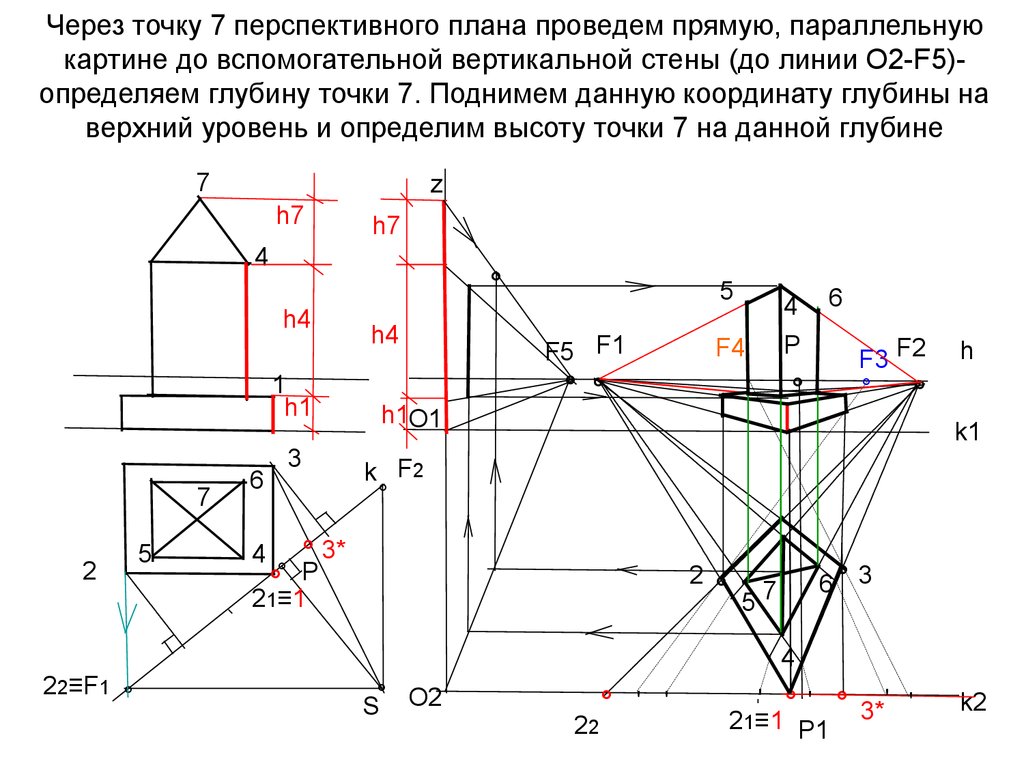
38. Через точку 7 перспективного плана проведем прямую, параллельную картине до вспомогательной вертикальной стены (до линии

О2-F5)определяем глубину точки 7. Поднимем данную координату глубины на
верхний уровень и определим высоту точки 7 на данной глубине
7
z
h7
h7
4
°
h4
1
h1
7
2
22≡F1 °
5
6
4
3
h4
h1О1
5
F5 F1
F4
° °
4
Р
°
6
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
6° 3
° 57
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

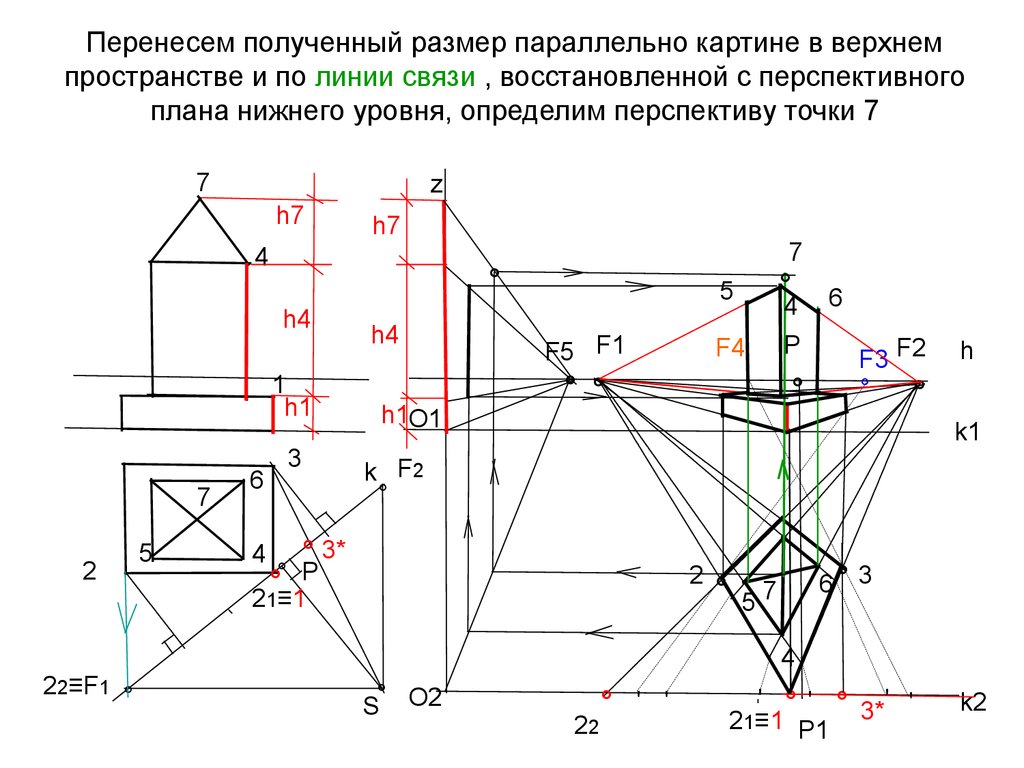
39. Перенесем полученный размер параллельно картине в верхнем пространстве и по линии связи , восстановленной с перспективного

плана нижнего уровня, определим перспективу точки 7
7
z
h7
h7
4
°
h4
1
h1
7
2
22≡F1 °
5
6
4
7
3
h4
h1О1
5
F5 F1
F4
° °
°
4
Р
°
6
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
6° 3
° 57
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2

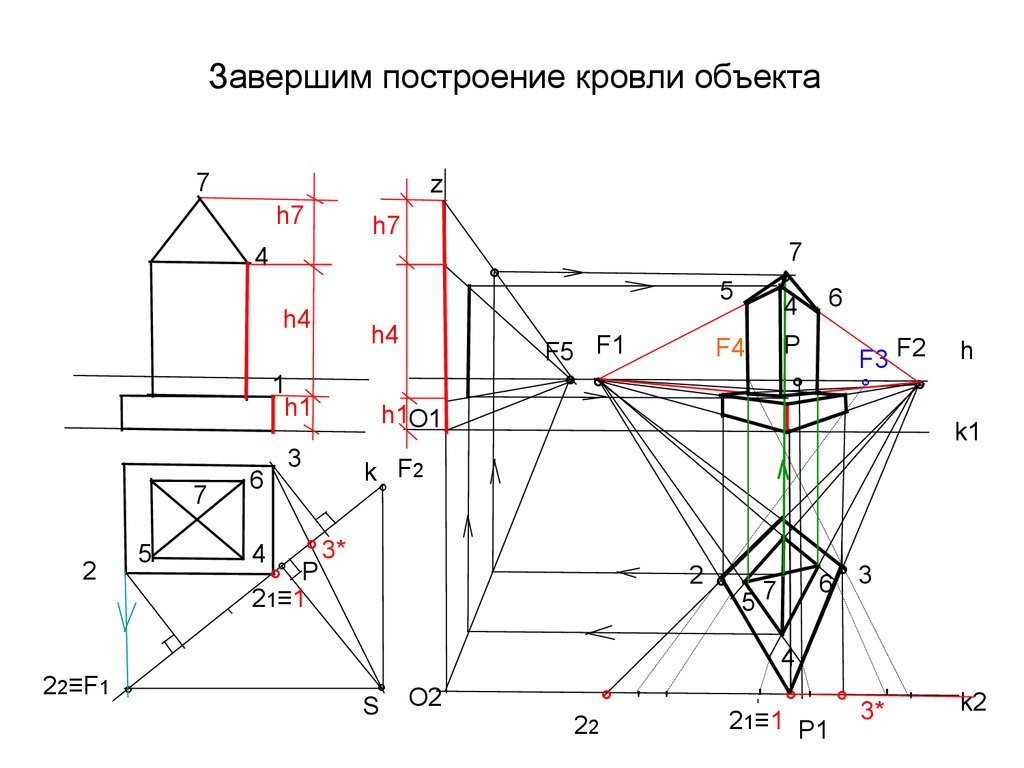
40. Завершим построение кровли объекта

7
z
h7
h7
4
°
h4
1
h1
7
2
22≡F1 °
5
6
4
7
3
h4
h1О1
5
F5 F1
F4
° °
°
4
Р
°
6
F3 F2
°
°
h
k1
k F2
°
° 3*
°° Р
2
21≡1
6° 3
° 57
4
S° O2
22
° ' '
' ° ' ° 3*' '
21≡1 Р1
k2