Построение перспективы объекта методом архитекторов с недоступной точкой схода

1. Лекция 21

Построение перспективы объекта методом архитекторов с
недоступной точкой схода
• Определение линии горизонта
• Определение положения картинной плоскости
• Определение положения наблюдателя (точки зрения)
• Построение точки схода прямых преимущественного
направления плана
• Пропорциональное деление отрезков прямых в
перспективе

2. Выбор положения линии горизонта

• Линия горизонта может располагаться на
любой высоте в зависимости от положения
глаз наблюдателя.
Отметим 3 наиболее применяемых положений
линии горизонта:
• На высоте 1,7 м(уровень глаз человека)
• С высоты птичьего полета (100 и более м)
• Может совпадать или быть ниже основания
картины

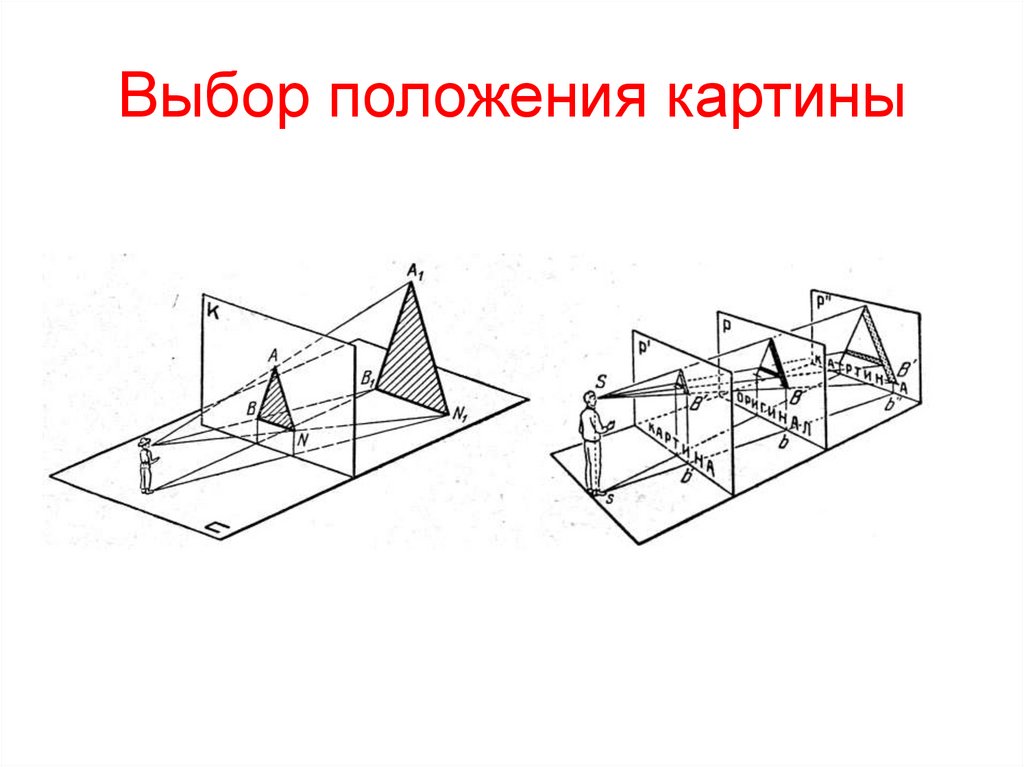
3. Выбор положения картины

Картина может располагаться :
• перед объектом;
• проходить через ребро объекта;
• За объектом
Угол наклона плоскости картины к
плоскости главного фасада α=30°

4. Выбор положения картины

5. Выбор положения картины

• Выберем положение
картины,
проходящей через
ребро 1 объекта. В
этом случае данное
ребро 1 будет
проецироваться в
натуральную
величину
α
●1

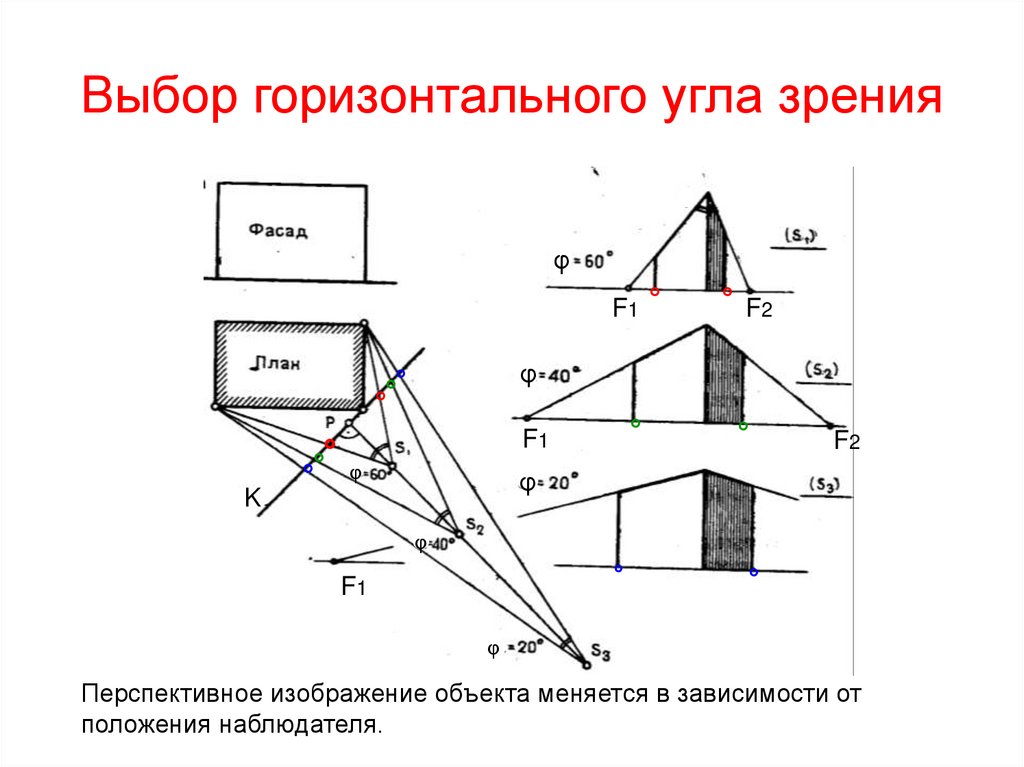
6. Выбор горизонтального угла зрения

φ
K
°
° F2
°
°
φ
°
°
°
°°
F1 °
F1
φ
F2
φ
φ
°
F1
°
φ
Перспективное изображение объекта меняется в зависимости от
положения наблюдателя.

7. Выбор положения наблюдателя

• Угол зрения φ= от 20° до 60°. Данное
значение получается, если дистанционное
расстояние L≤ PS ≤ 2L, где L-длина объекта
• Чтобы получить оптимальный угол зрения,
необходимо из концов плана объекта
опустить к плоскости картины
перпендикуляры, полученное расстояние
разделить на 3 части. Две части относятся к
главному фасаду, одна часть- к боковому

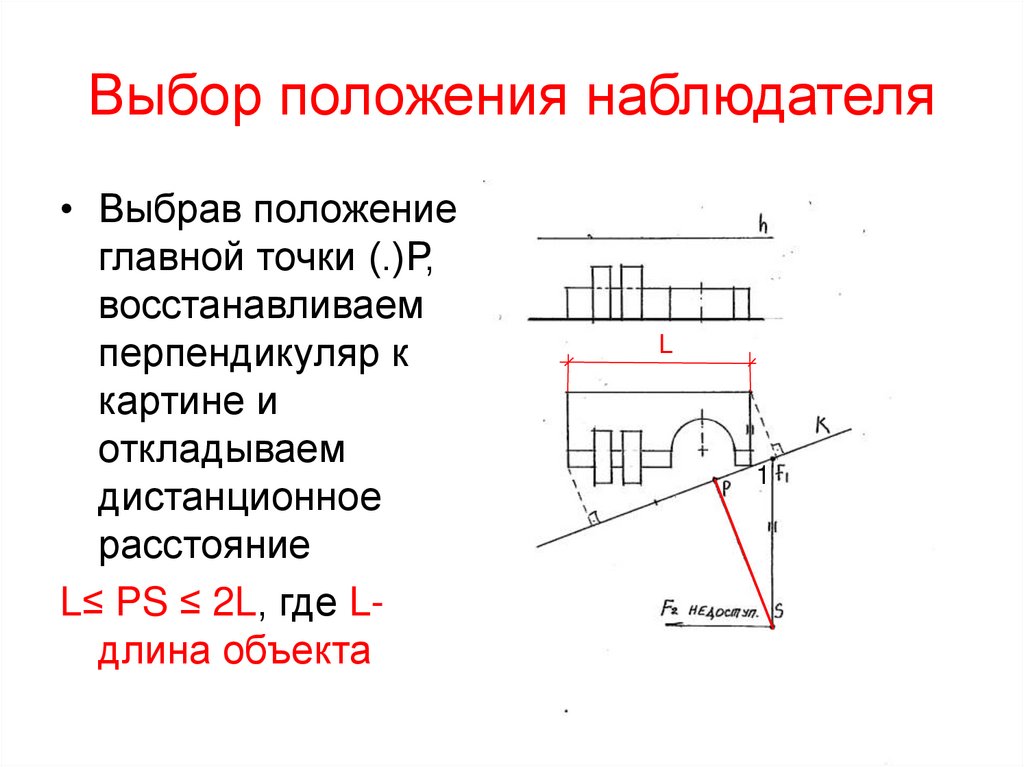
8. Выбор положения наблюдателя

• Выбрав положение
главной точки (.)Р,
восстанавливаем
перпендикуляр к
картине и
откладываем
дистанционное
расстояние
L≤ PS ≤ 2L, где Lдлина объекта
L
1

9. Построение точек схода

• Чтобы построить точку схода любой
прямой, необходимо через глаза
наблюдателя (точку S) провести
прямую, параллельную данной прямой
и найти ее пересечение с картиной
• (.) F2 оказывается недоступной.
Следовательно будем строить
перспективу с одной точкой схода

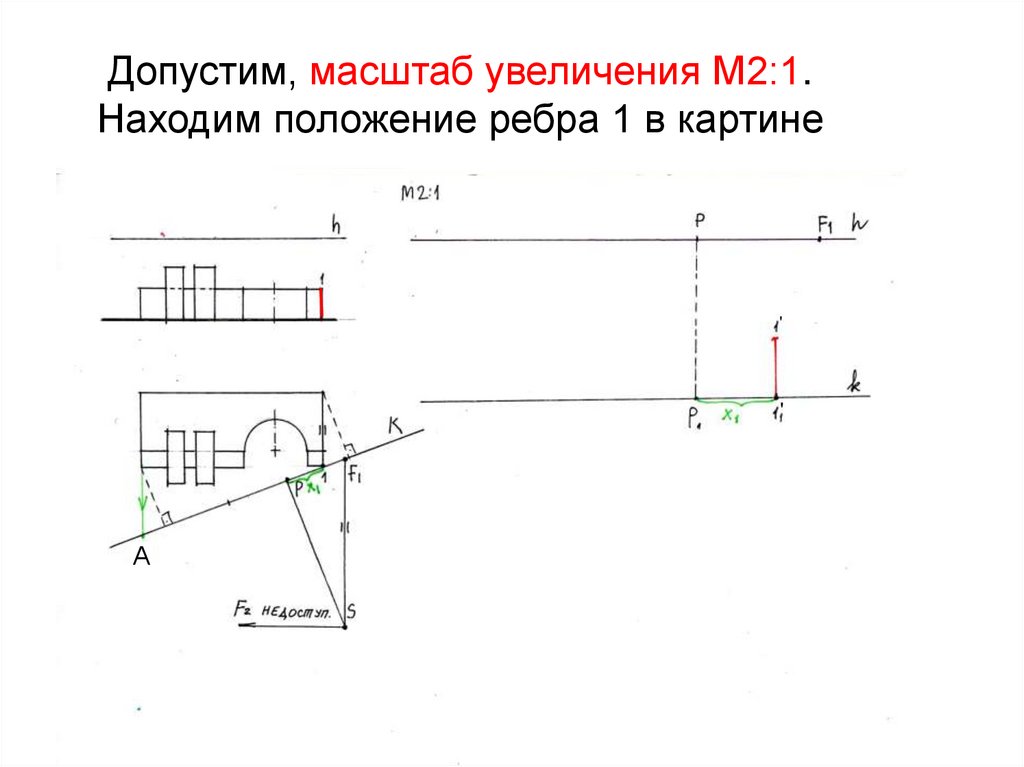
10. Выбор масштаба перспективы

Масштаб увеличения перспективного
изображения зависит от расстояния от
(.)F1 до (.)А, где
• (.)F1- точка схода вертикальных
прямых плана;
• (.)А – точка выдвижения крайней левой
плоскости объекта в картину

11. Допустим, масштаб увеличения М2:1. Находим положение ребра 1 в картине

'
'
А

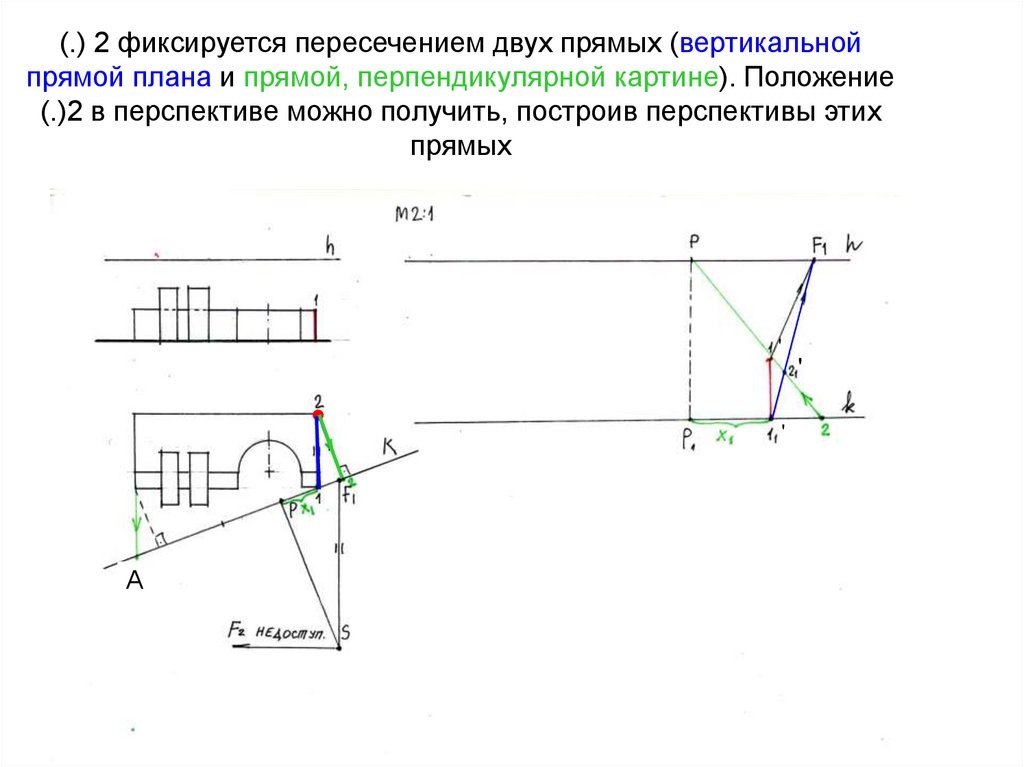
12. (.) 2 фиксируется пересечением двух прямых (вертикальной прямой плана и прямой, перпендикулярной картине). Положение (.)2 в

перспективе можно получить, построив перспективы этих
прямых
'
'
А
'

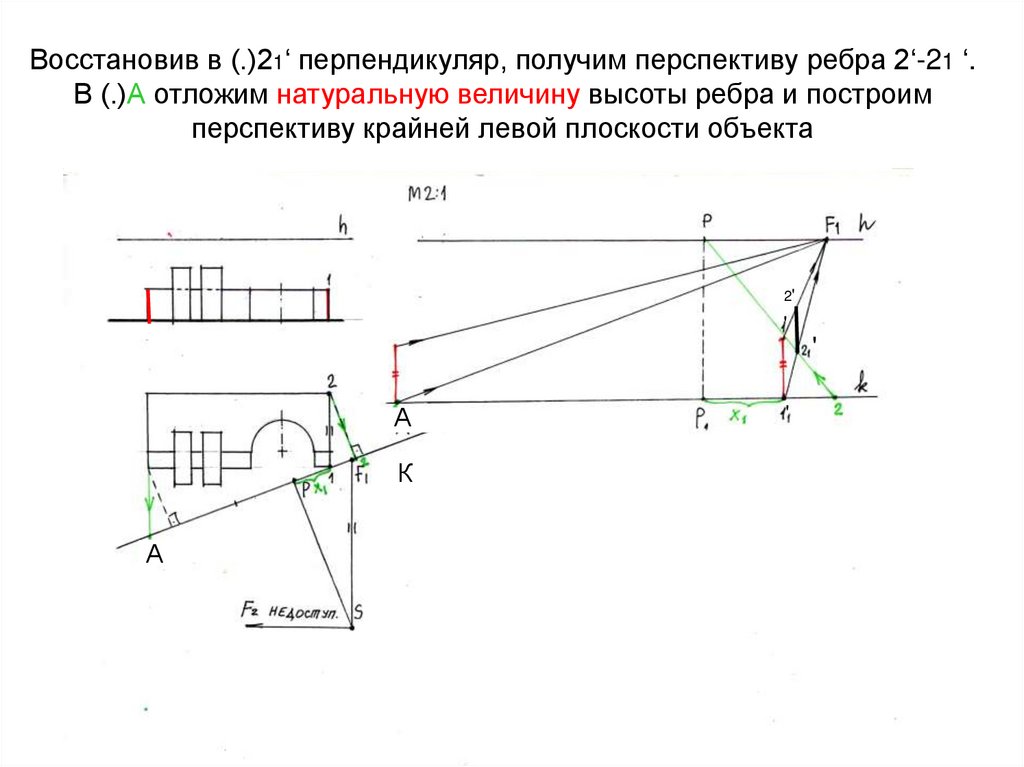
13. Восстановив в (.)21‘ перпендикуляр, получим перспективу ребра 2‘-21 ‘. В (.)А отложим натуральную величину высоты ребра и

построим
перспективу крайней левой плоскости объекта
2'
'
'
А
К
А
'

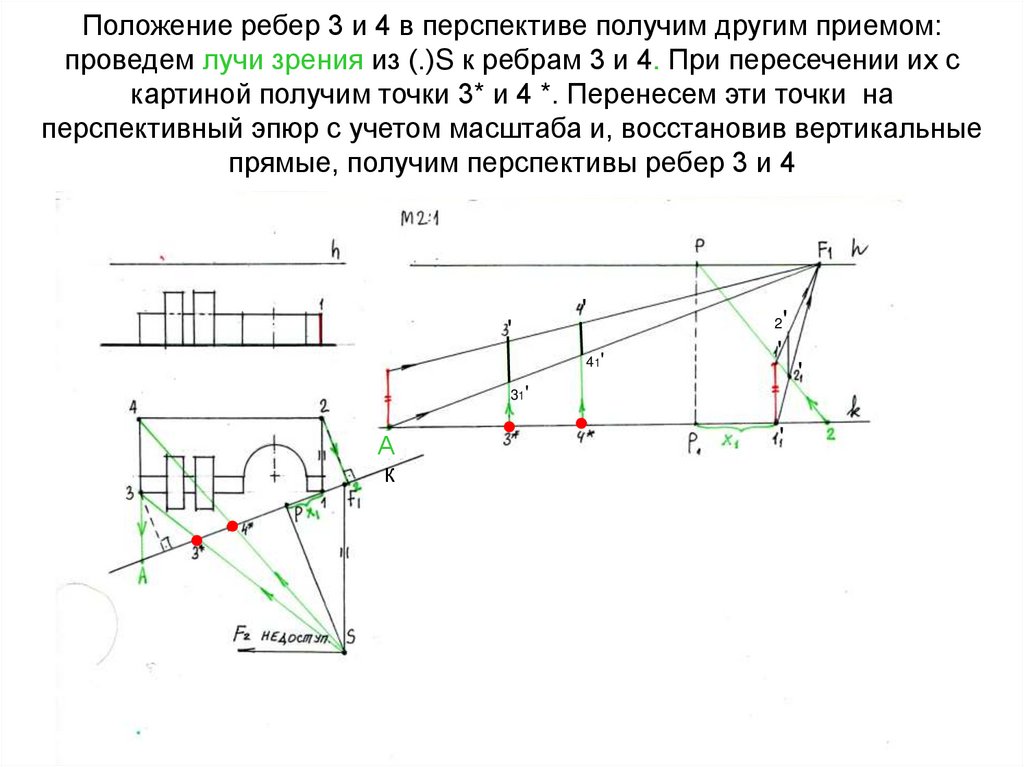
14. Положение ребер 3 и 4 в перспективе получим другим приемом: проведем лучи зрения из (.)S к ребрам 3 и 4. При пересечении их с

картиной получим точки 3* и 4 *. Перенесем эти точки на
перспективный эпюр с учетом масштаба и, восстановив вертикальные
прямые, получим перспективы ребер 3 и 4
'
'
41'
'
2
'
31'
А
к
'
'

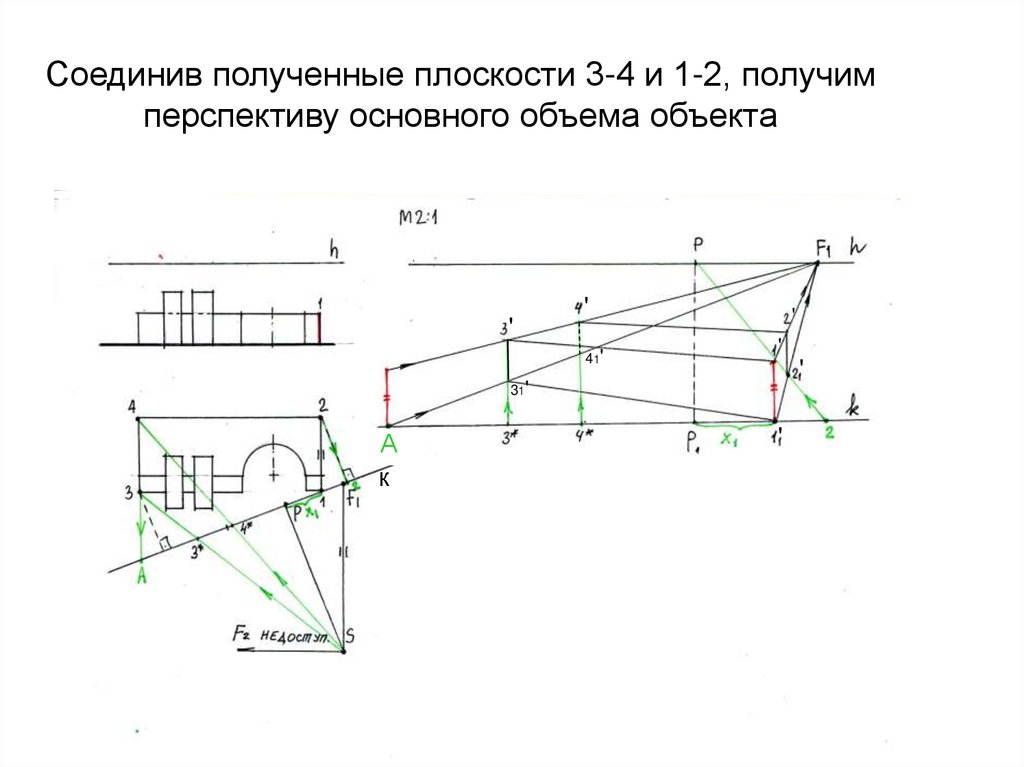
15. Соединив полученные плоскости 3-4 и 1-2, получим перспективу основного объема объекта

'
'
41'
'
'
'
31'
А
к
'

16. пропорциональное деление отрезка прямой

• Для дальнейших построений
используем теорему Фалеса о
пропорциональном делении отрезка
(если на одной стороне угла отложить
равные между собой отрезки и через их
концы провести параллельные прямые,
то на другой стороне угла также
отложатся равные между собой
отрезки).

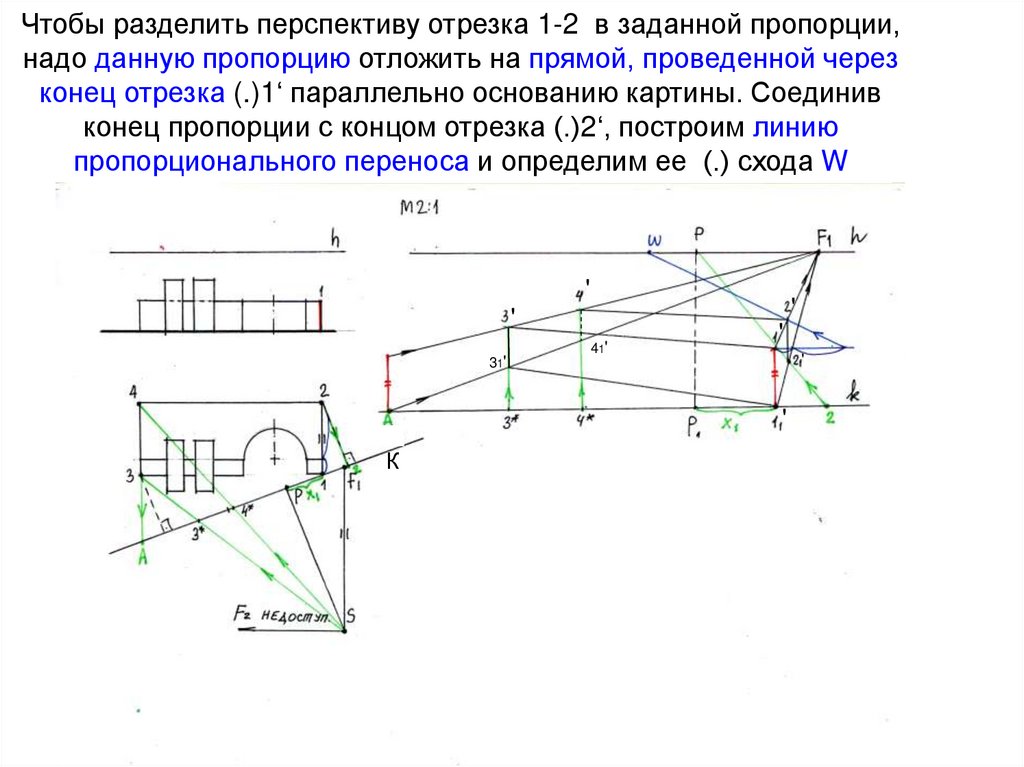
17. Чтобы разделить перспективу отрезка 1-2 в заданной пропорции, надо данную пропорцию отложить на прямой, проведенной через конец

отрезка (.)1‘ параллельно основанию картины. Соединив
конец пропорции с концом отрезка (.)2‘, построим линию
пропорционального переноса и определим ее (.) схода W
'
'
'
31'
41'
'
'
'
К

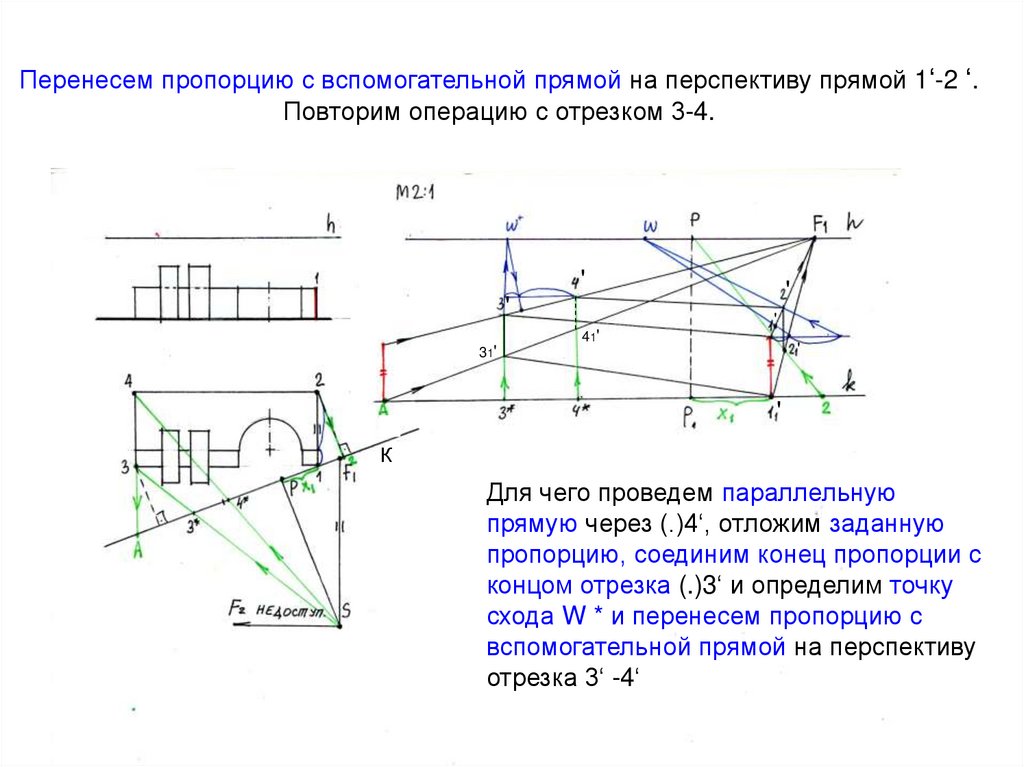
18. Перенесем пропорцию с вспомогательной прямой на перспективу прямой 1‘-2 ‘. Повторим операцию с отрезком 3-4.

'
'
31'
'
'
41'
'
'
К
Для чего проведем параллельную
прямую через (.)4‘, отложим заданную
пропорцию, соединим конец пропорции с
концом отрезка (.)3‘ и определим точку
схода W * и перенесем пропорцию с
вспомогательной прямой на перспективу
отрезка 3‘ -4‘

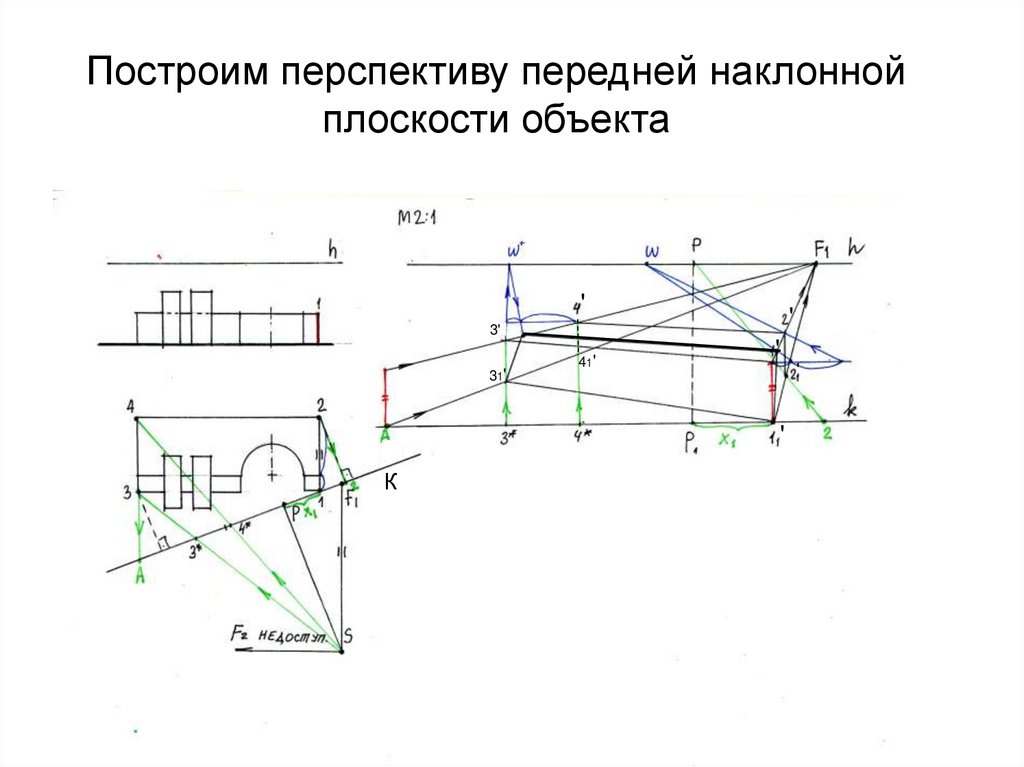
19. Построим перспективу передней наклонной плоскости объекта

'
'
3'
31'
41'
'
'
К
'

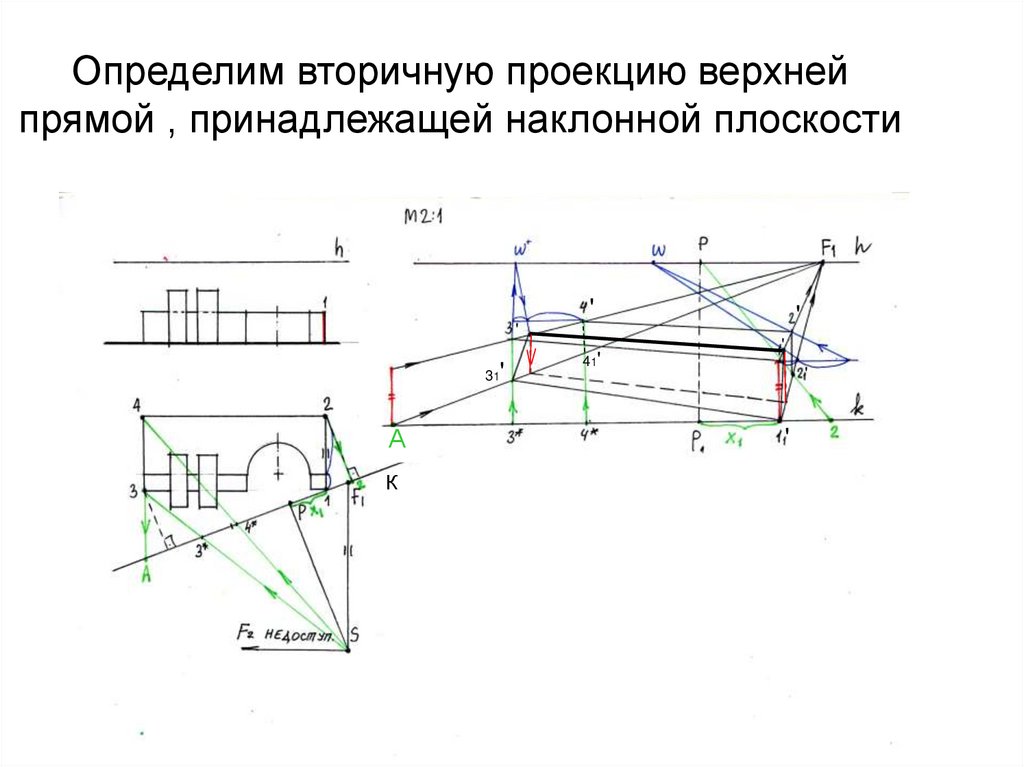
20. Определим вторичную проекцию верхней прямой , принадлежащей наклонной плоскости

'
'
'
41'
'
'
'
31
А
К
'

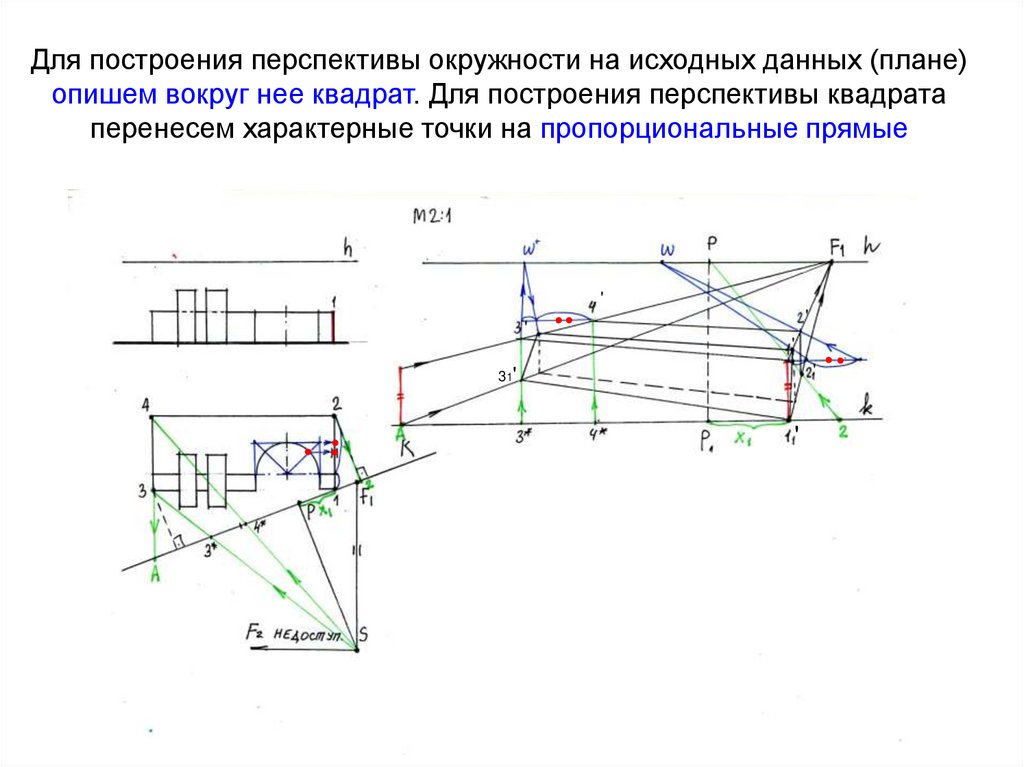
21. Для построения перспективы окружности на исходных данных (плане) опишем вокруг нее квадрат. Для построения перспективы квадрата

перенесем характерные точки на пропорциональные прямые
'
'
'
●
'
'
31'
'
●

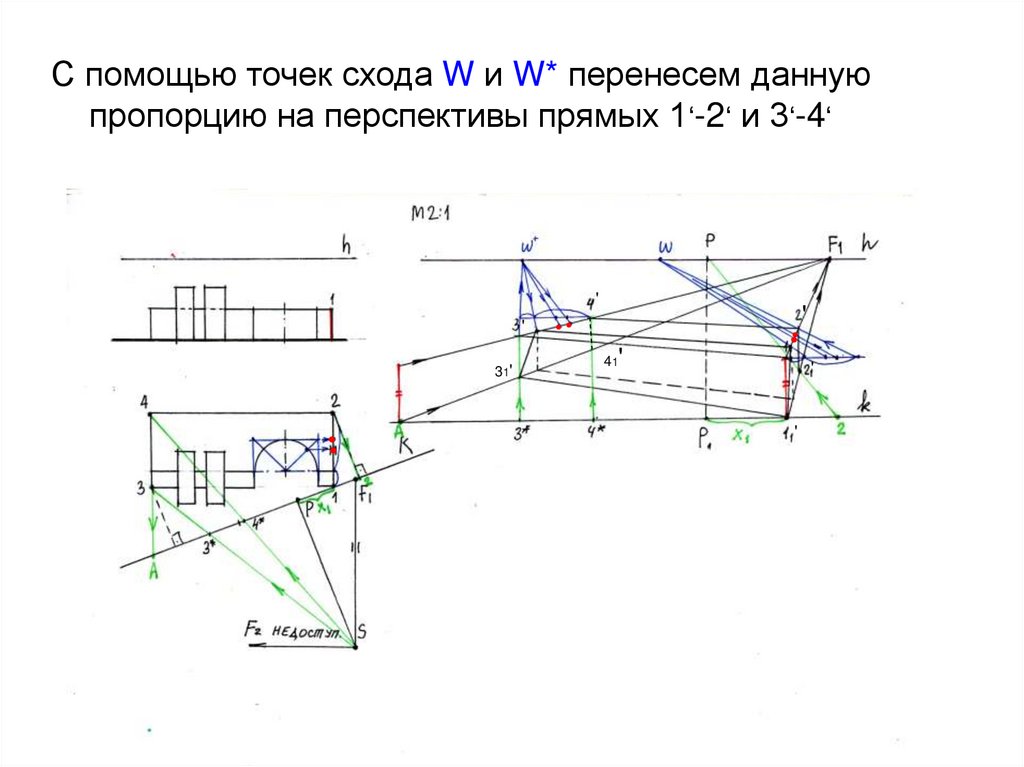
22. С помощью точек схода W и W* перенесем данную пропорцию на перспективы прямых 1‘-2‘ и 3‘-4‘

'
'
31'
●
●
'
41
'
'
'

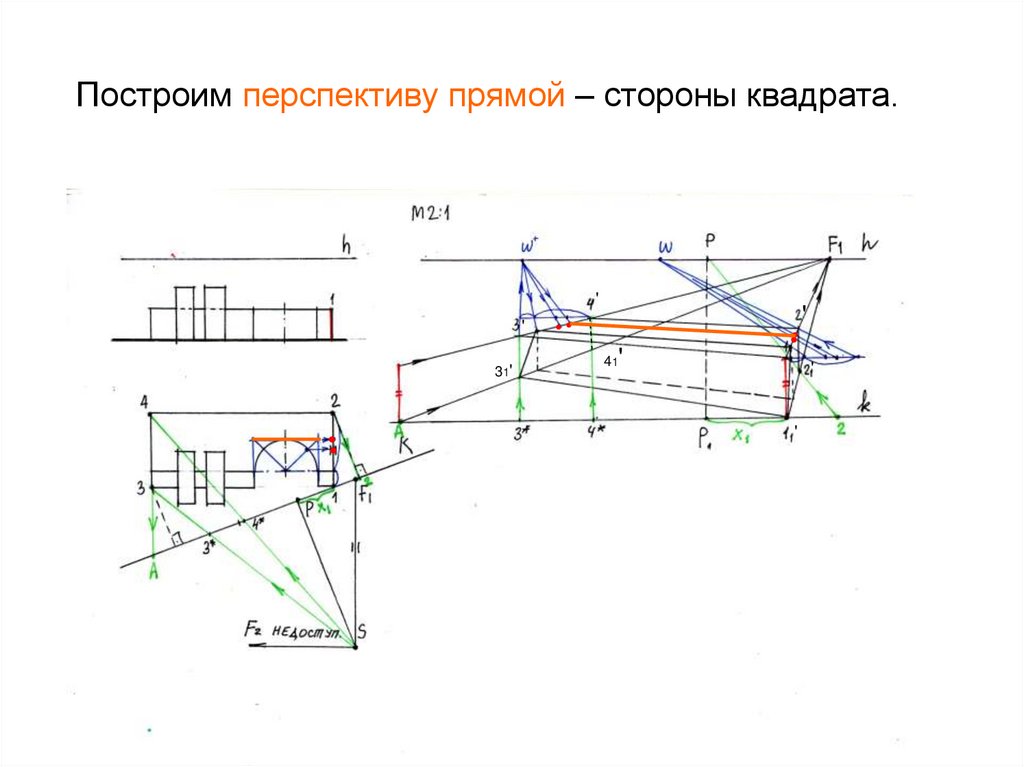
23. Построим перспективу прямой – стороны квадрата.

'
'
31'
●
●
'
41
'
'
'

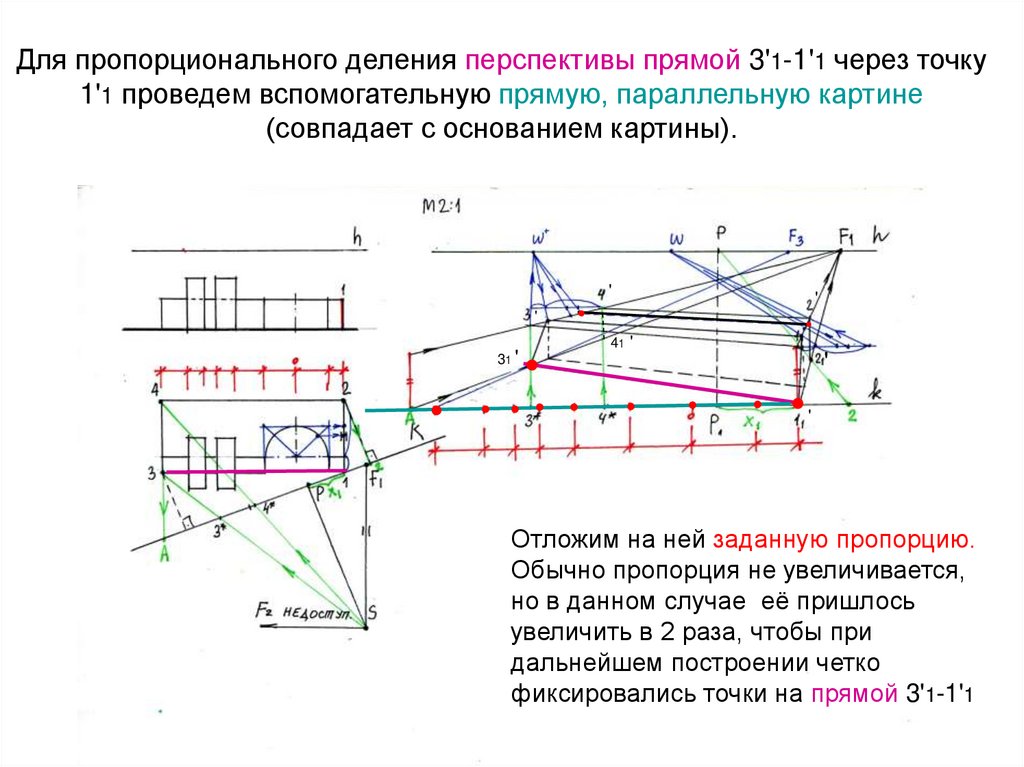
24. Для пропорционального деления перспективы прямой 3'1-1'1 через точку 1'1 проведем вспомогательную прямую, параллельную картине

(совпадает с основанием картины).
'
'
31 '
41
●
'
'
'
●'
Отложим на ней заданную пропорцию.
Обычно пропорция не увеличивается,
но в данном случае её пришлось
увеличить в 2 раза, чтобы при
дальнейшем построении четко
фиксировались точки на прямой 3'1-1'1

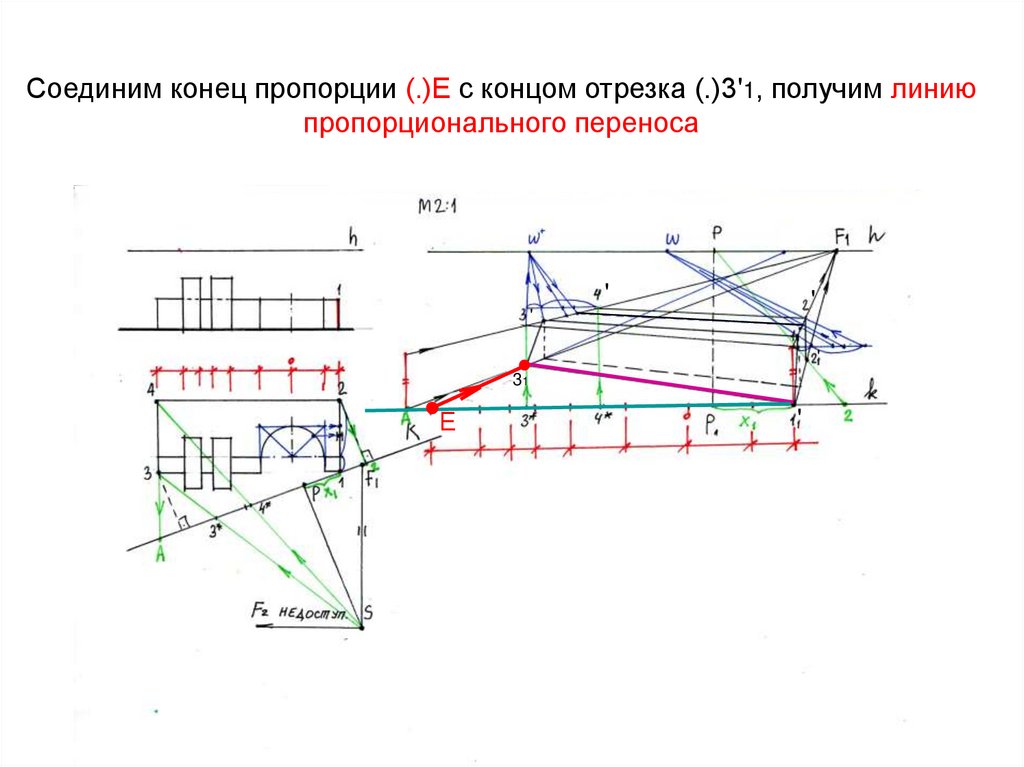
25. Соединим конец пропорции (.)Е с концом отрезка (.)3'1, получим линию пропорционального переноса

'
'
'
'
31
Е
'

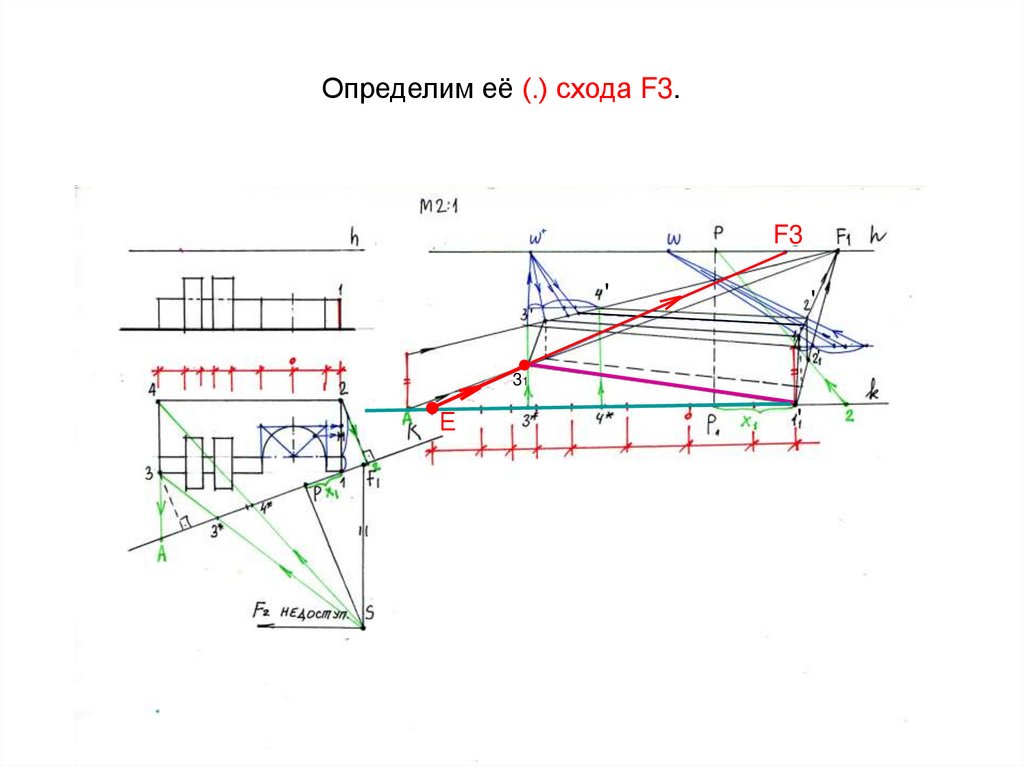
26. Определим её (.) схода F3.

F3
'
'
'
'
31
Е
'

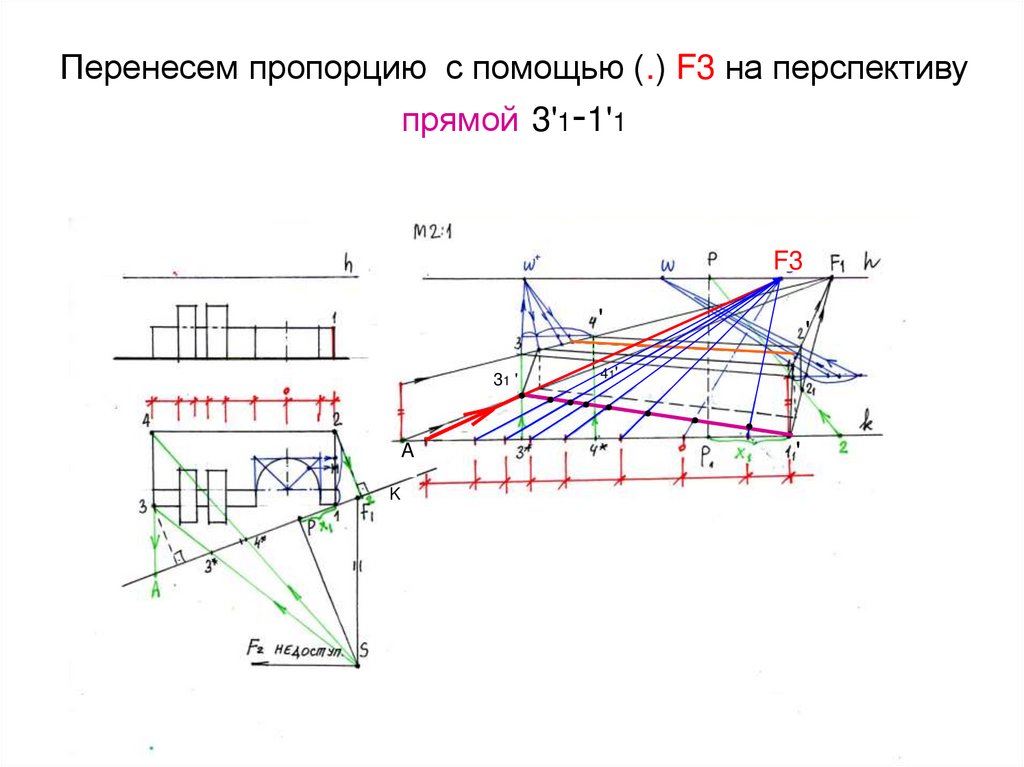
27. Перенесем пропорцию с помощью (.) F3 на перспективу прямой 3'1-1'1

F3
'
41'
31 '
A
K
'
● ●
'

28. Построим перспективу половины квадрата, для чего соответствующие точки поднимем до верхней горизонтальной плоскости и уведем

прямые в перспективу в
точку схода F1. Построим перспективы диагоналей
'
31'
'
'
41'
'
'

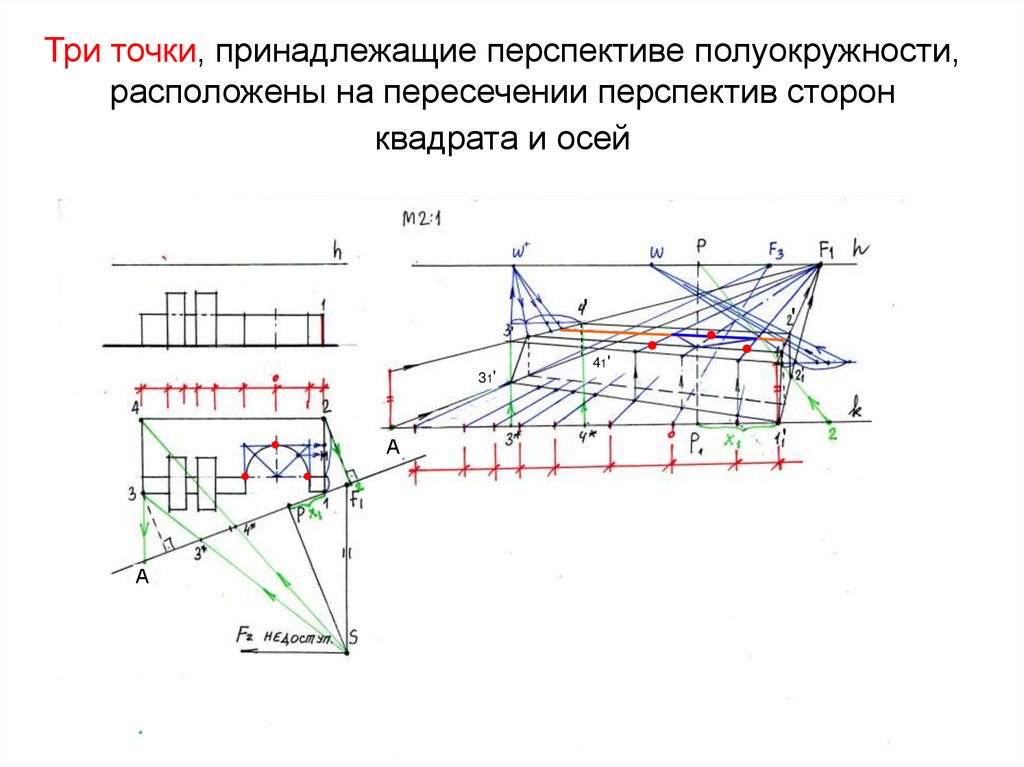
29. Три точки, принадлежащие перспективе полуокружности, расположены на пересечении перспектив сторон квадрата и осей

'
'
31'
А
А
41'
'
'
'

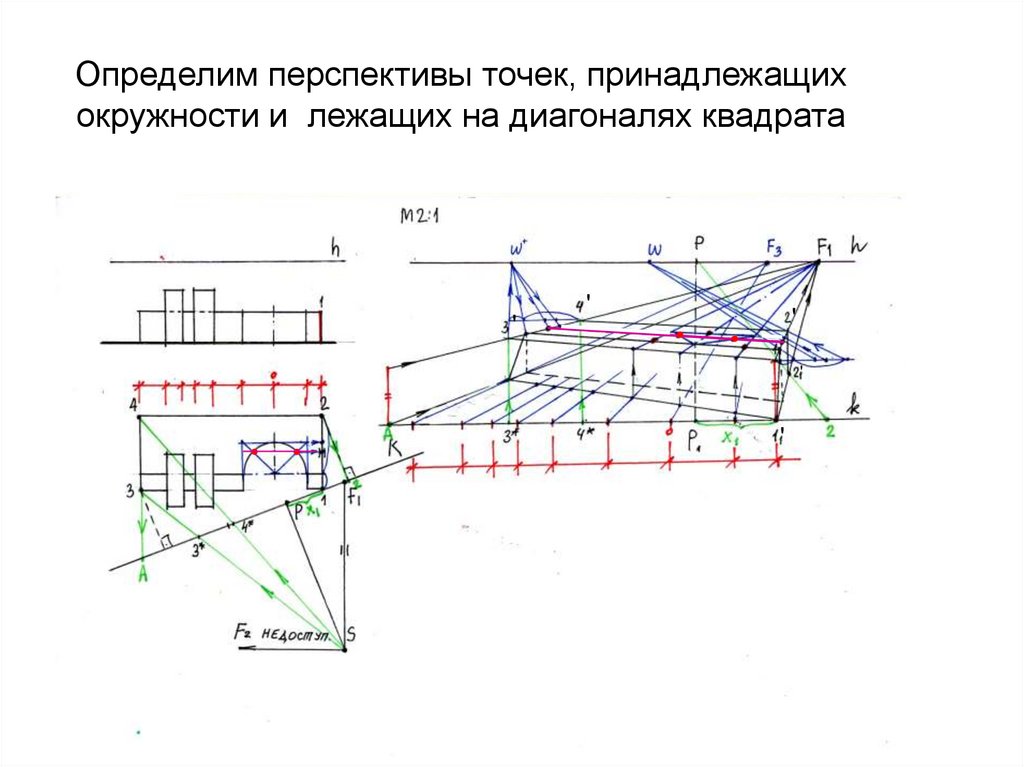
30. Определим перспективы точек, принадлежащих окружности и лежащих на диагоналях квадрата

'
'
'
'
'

31. Построим перспективу полуокружности, лежащей на верхней плоскости призмы.

'
'
'
'
31'
'

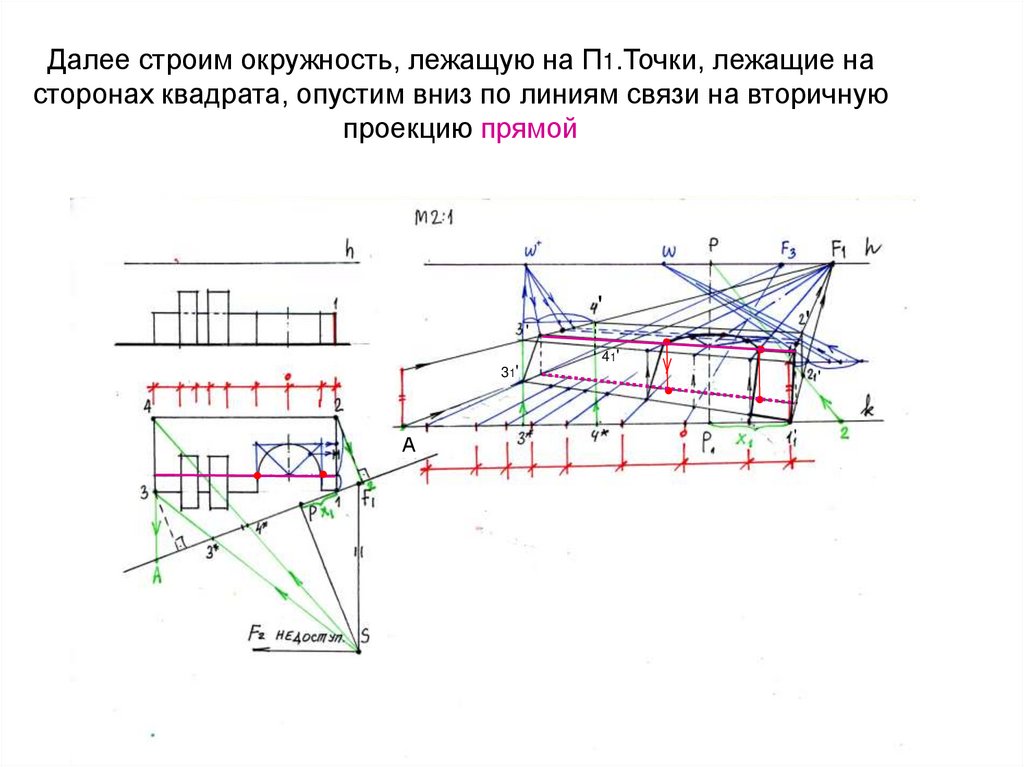
32. Далее строим окружность, лежащую на П1.Точки, лежащие на сторонах квадрата, опустим вниз по линиям связи на вторичную проекцию

прямой
'
'
31'
А
41'
'
'
'

33. Для построения выреза используем вертикальные плоскости, проходящие через характерные точки окружности. Точка схода

горизонтальных прямых этих плоскостей F1
'
31'
41'
'
'
'

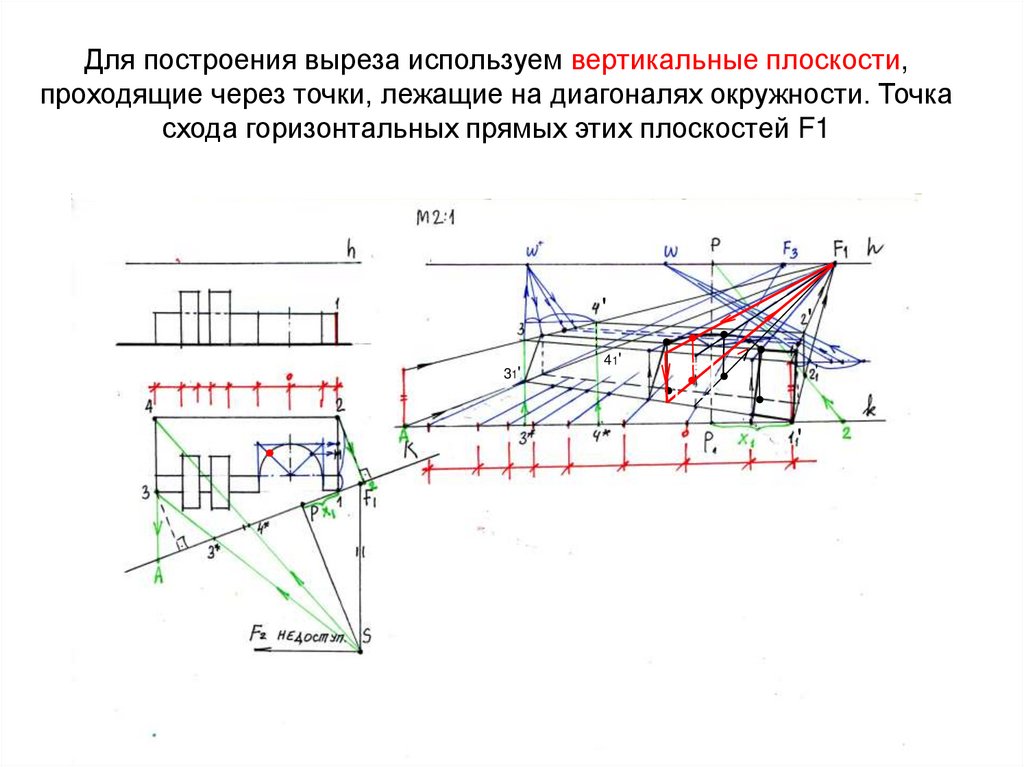
34. Для построения выреза используем вертикальные плоскости, проходящие через точки, лежащие на диагоналях окружности. Точка схода

горизонтальных прямых этих плоскостей F1
'
31'
●
41'
'
'
'

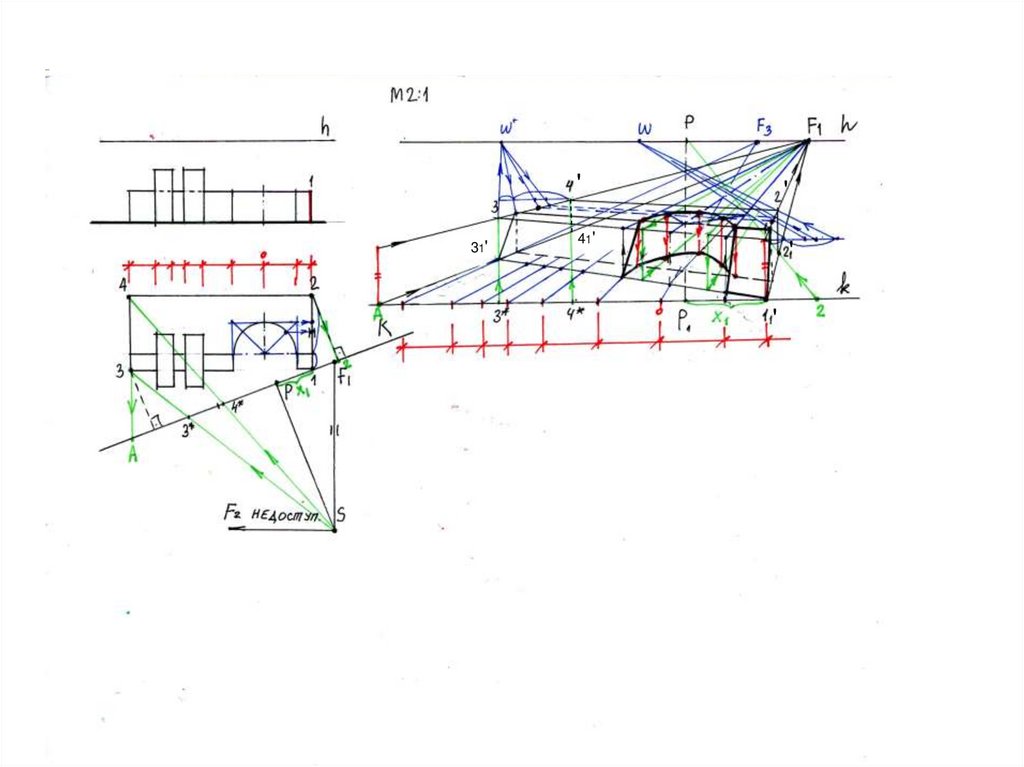
35.

'
31'
'
41'
'
'

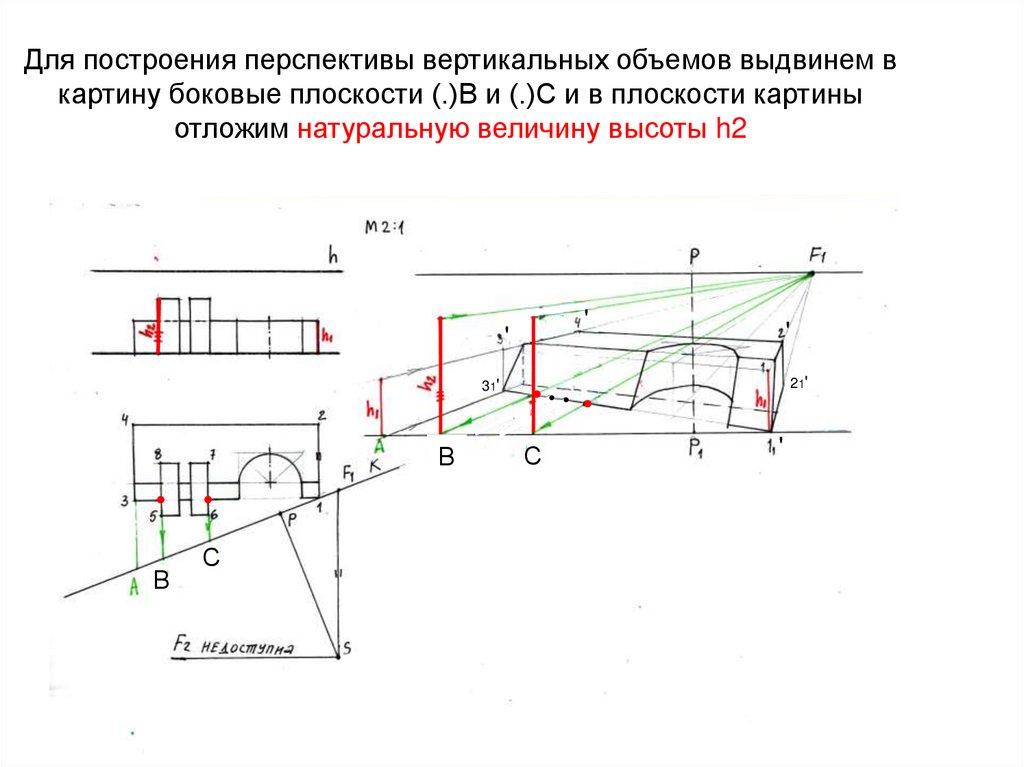
36. Для построения перспективы вертикальных объемов выдвинем в картину боковые плоскости (.)В и (.)С и в плоскости картины отложим

натуральную величину высоты h2
'
'
31'
В
В
С
С
●
'
21'
'

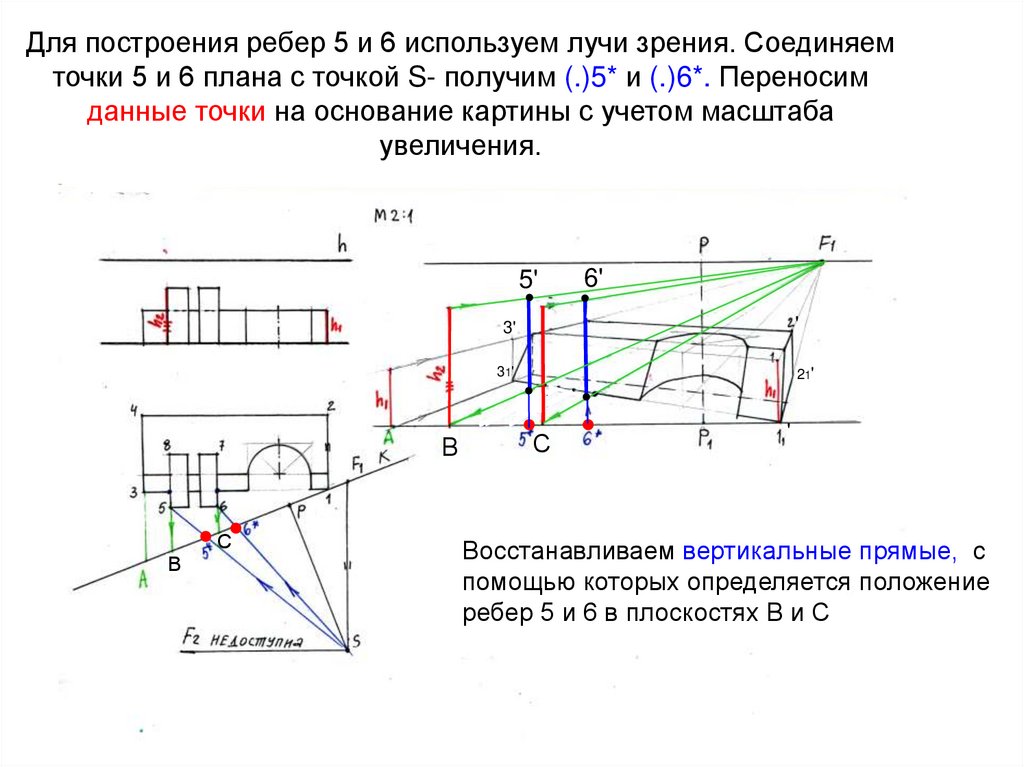
37. Для построения ребер 5 и 6 используем лучи зрения. Соединяем точки 5 и 6 плана с точкой S- получим (.)5* и (.)6*. Переносим

данные точки на основание картины с учетом масштаба
увеличения.
5'
6'
'
3'
31'
В
● С
В
21'
С
'
Восстанавливаем вертикальные прямые, с
помощью которых определяется положение
ребер 5 и 6 в плоскостях В и С

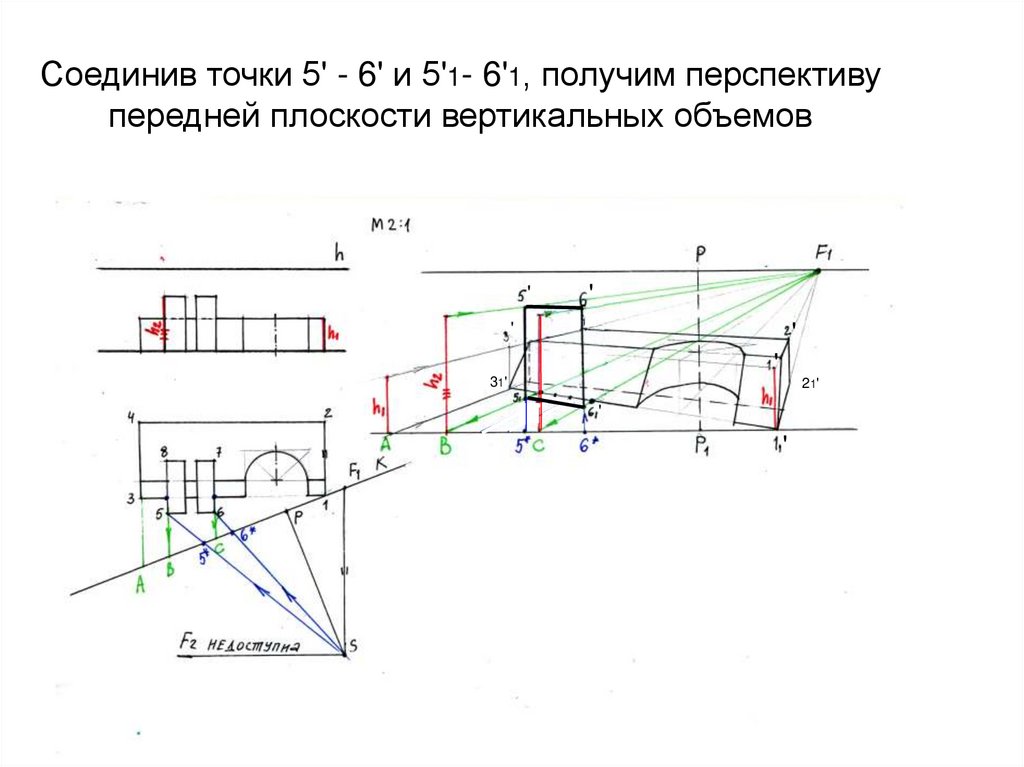
38. Соединив точки 5' - 6' и 5'1- 6'1, получим перспективу передней плоскости вертикальных объемов

'
'
'
'
'
31'
21'
'
'

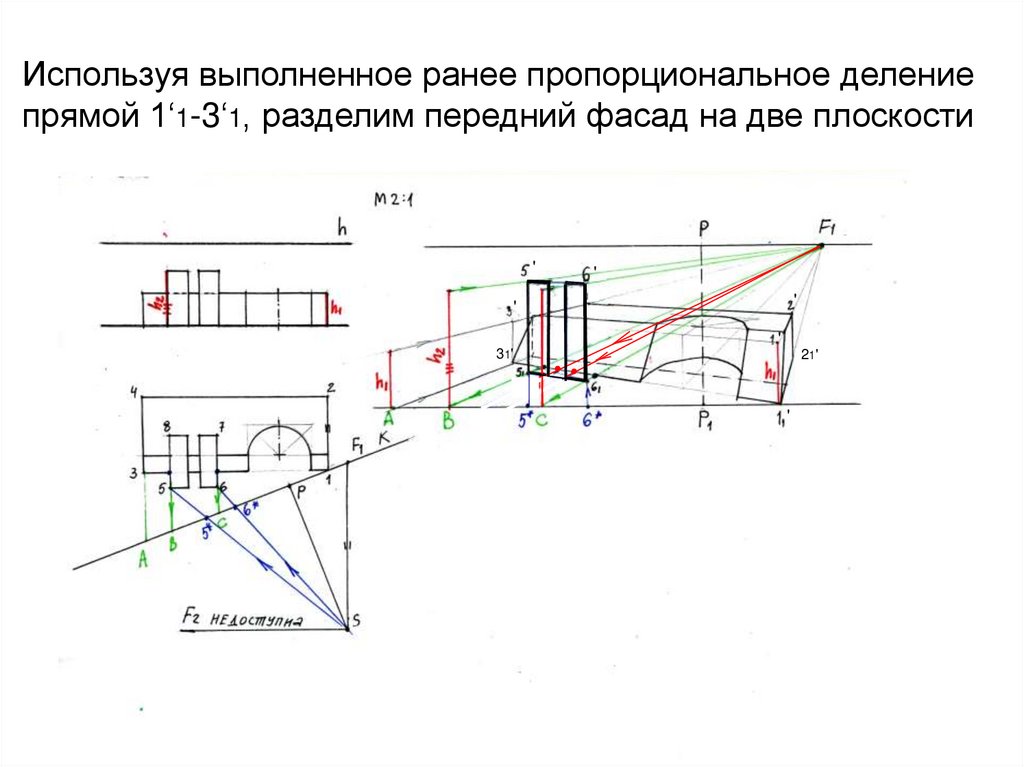
39. Используя выполненное ранее пропорциональное деление прямой 1‘1-3‘1, разделим передний фасад на две плоскости

'
'
'
'
'
31'
21'
●
'

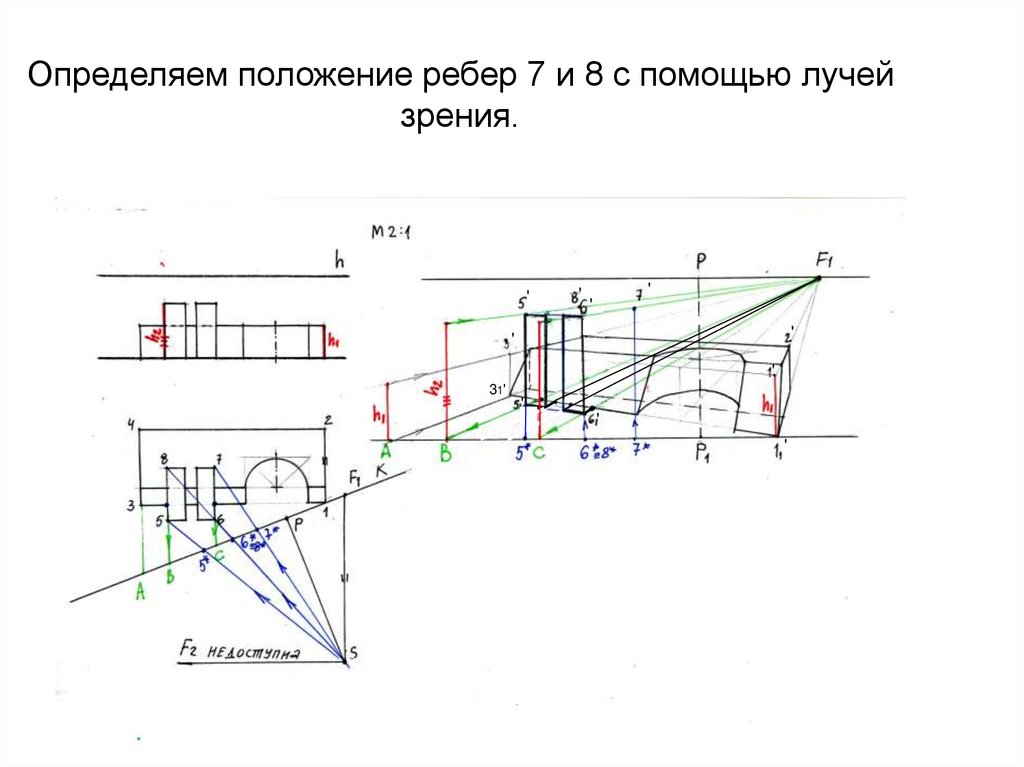
40. Определяем положение ребер 7 и 8 с помощью лучей зрения.

'
'
'
'
'
'
'
31'
'
'
'

41. Строим перспективу боковых плоскостей вертикальных объемов

'
'
'
'
'
31'
71●'
'
'
'
'

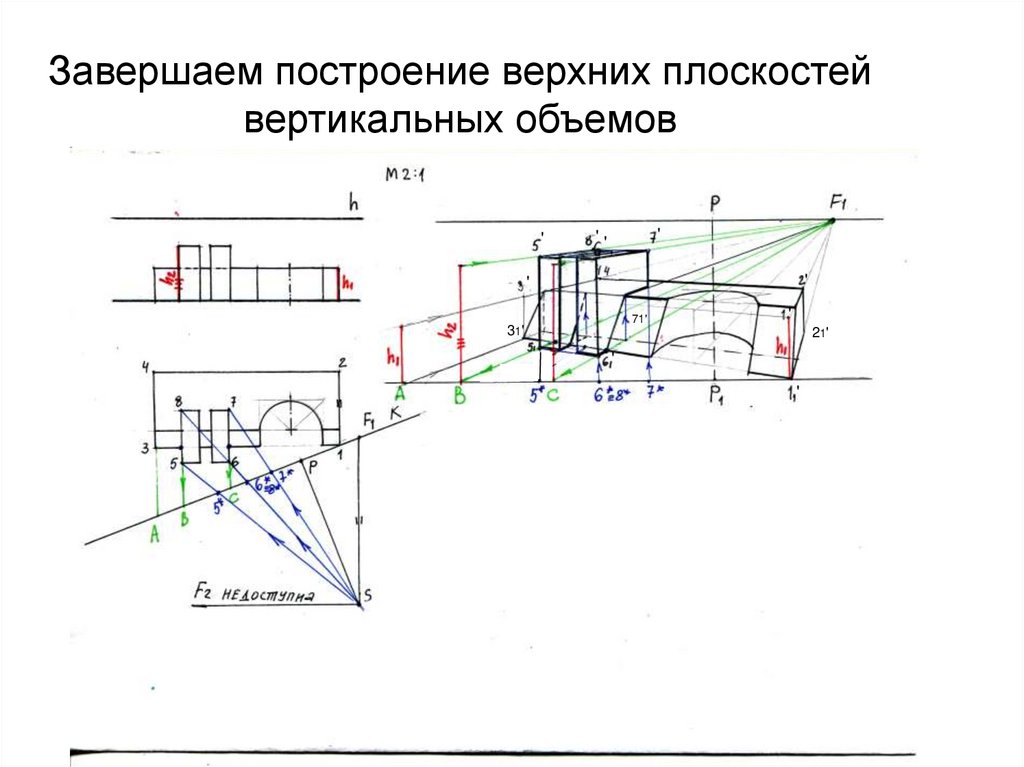
42. Завершаем построение верхних плоскостей вертикальных объемов

'
'
''
'
'
71'
31'
'
21'
'
'

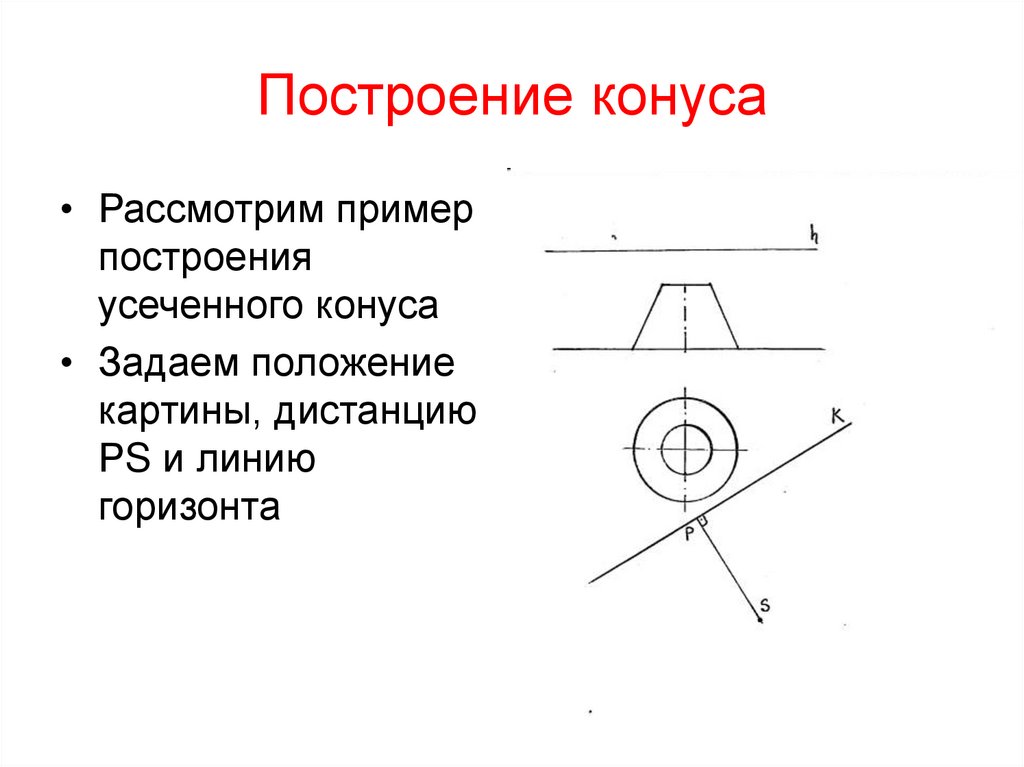
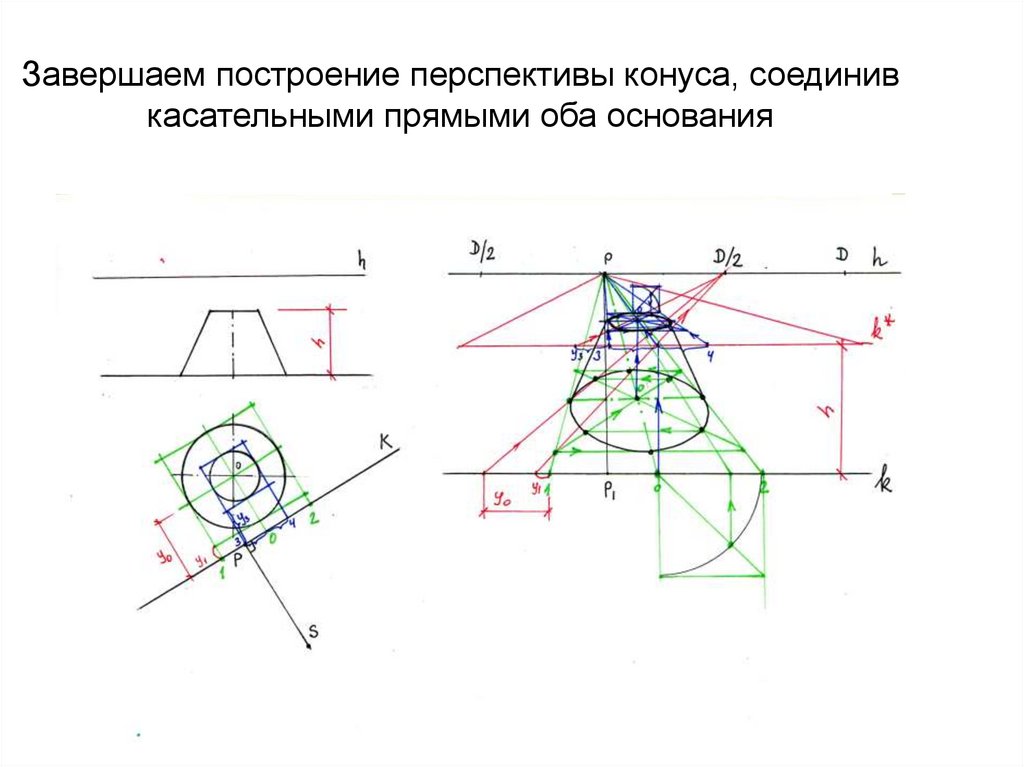
43. Построение конуса

• Рассмотрим пример
построения
усеченного конуса
• Задаем положение
картины, дистанцию
РS и линию
горизонта

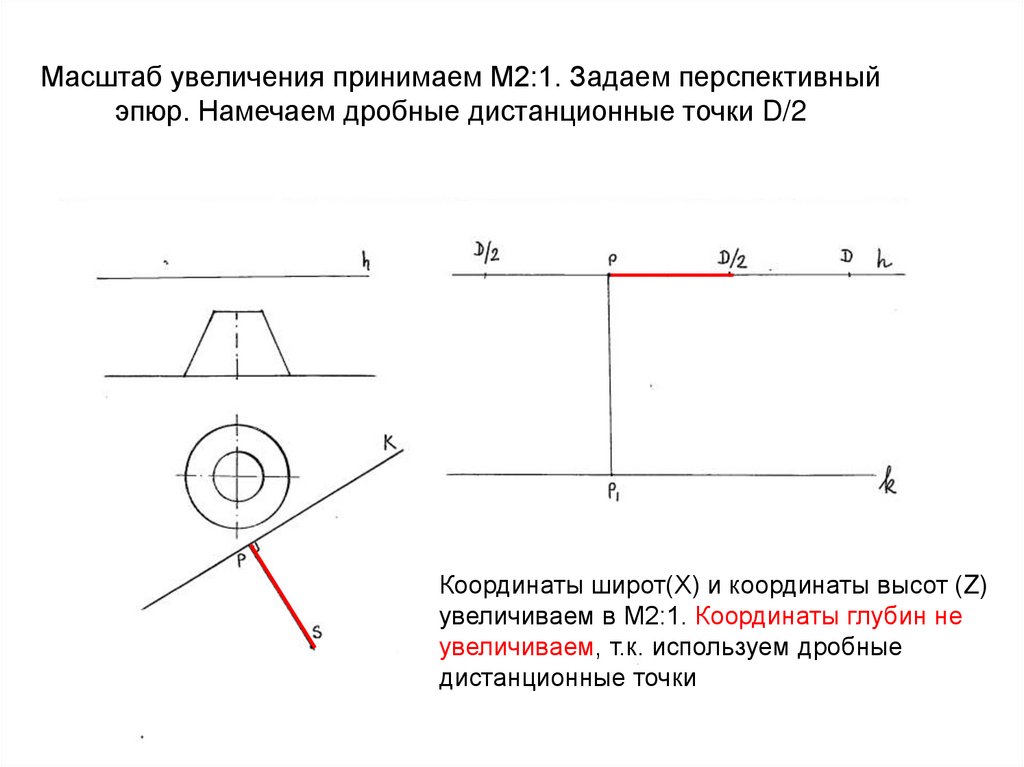
44. Масштаб увеличения принимаем М2:1. Задаем перспективный эпюр. Намечаем дробные дистанционные точки D/2

Координаты широт(Х) и координаты высот (Z)
увеличиваем в М2:1. Координаты глубин не
увеличиваем, т.к. используем дробные
дистанционные точки

45. Построим вокруг окружности квадрат со сторонами параллельными и перпендикулярными картине. Определяем перспективы

перпендикулярных прямых, для чего переносим
(..)1, 0 и 2 на основание картины с учетом масштаба увеличения

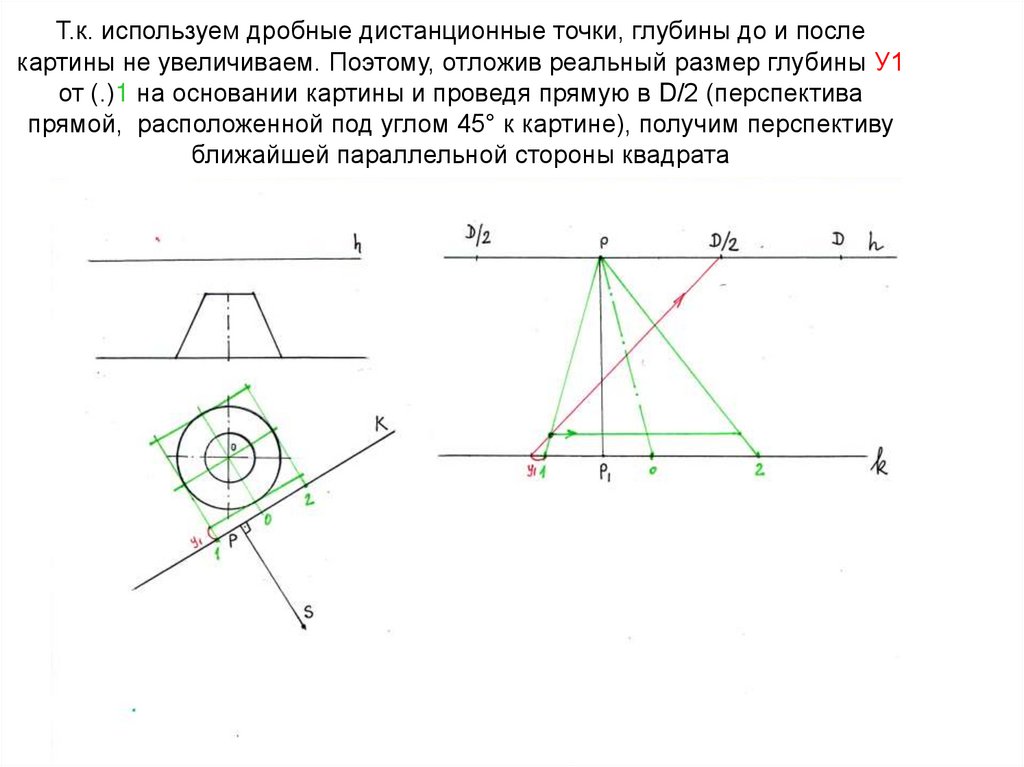
46. Т.к. используем дробные дистанционные точки, глубины до и после картины не увеличиваем. Поэтому, отложив реальный размер

глубины У1
от (.)1 на основании картины и проведя прямую в D/2 (перспектива
прямой, расположенной под углом 45° к картине), получим перспективу
ближайшей параллельной стороны квадрата

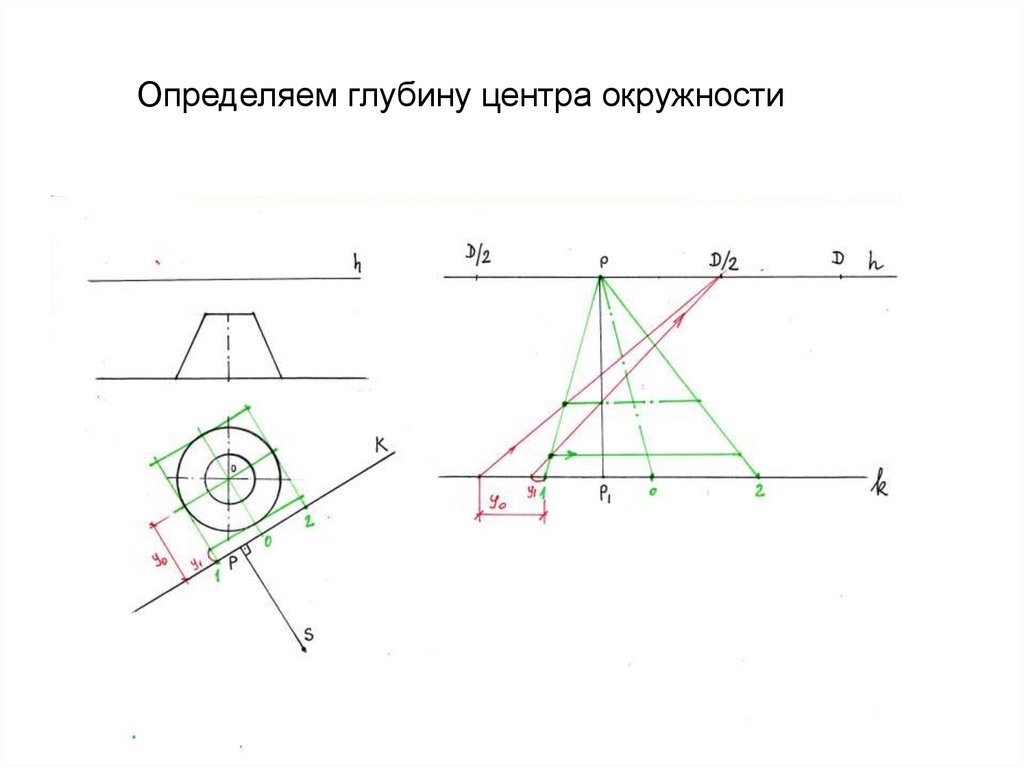
47. Определяем глубину центра окружности

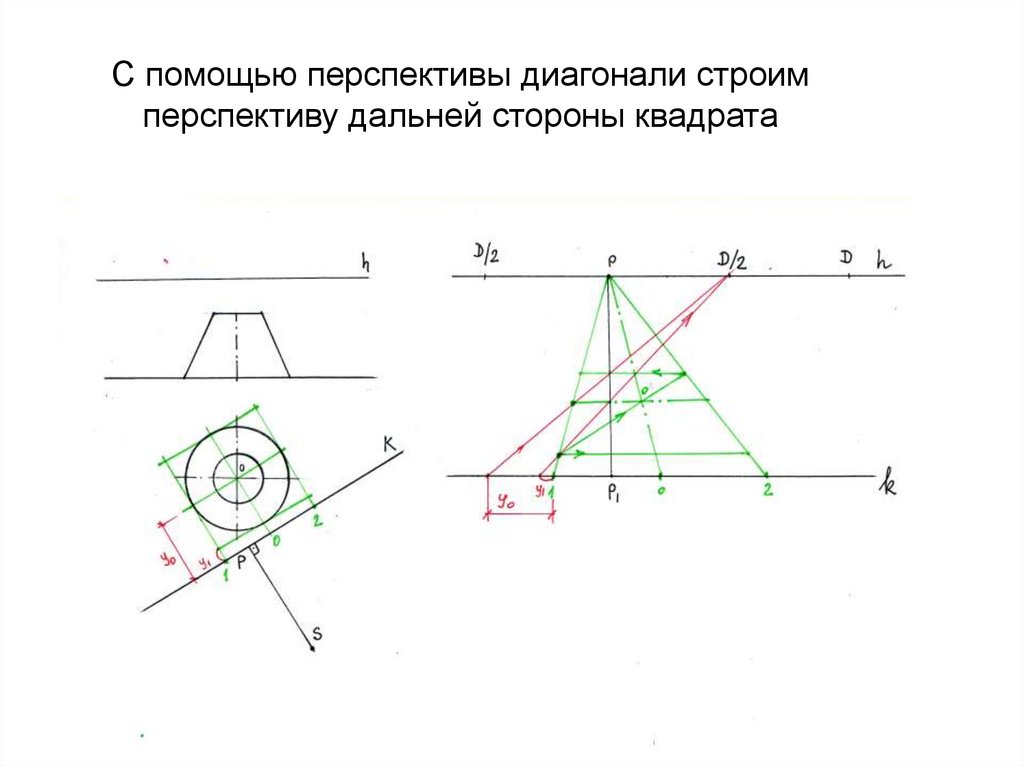
48. С помощью перспективы диагонали строим перспективу дальней стороны квадрата

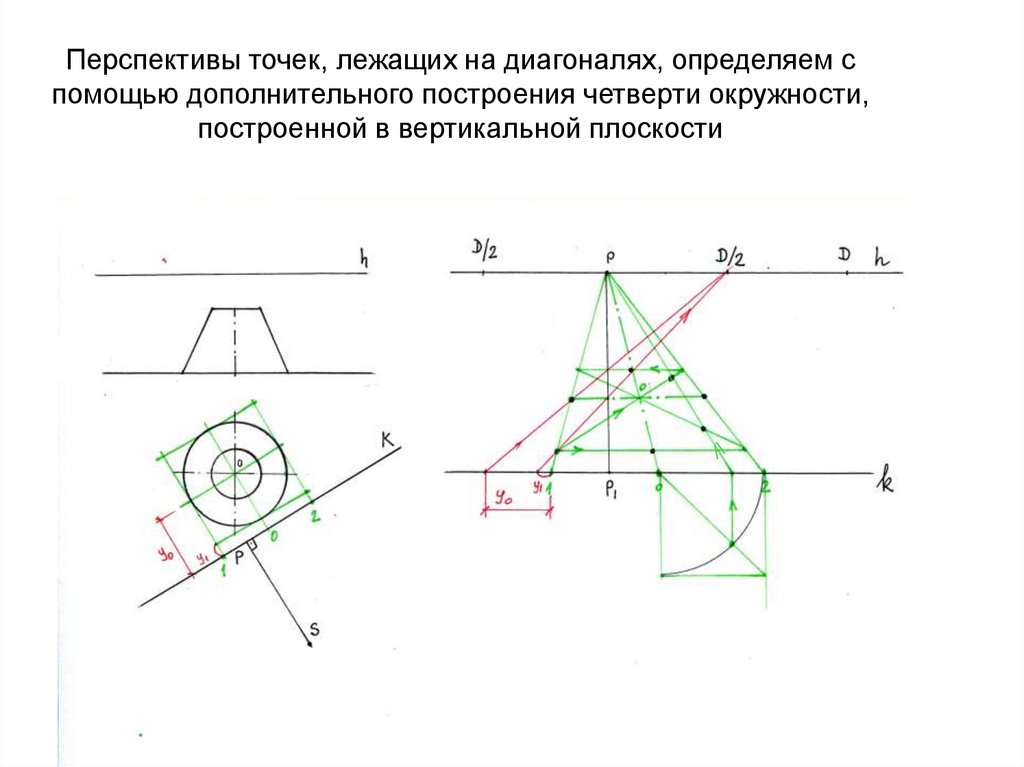
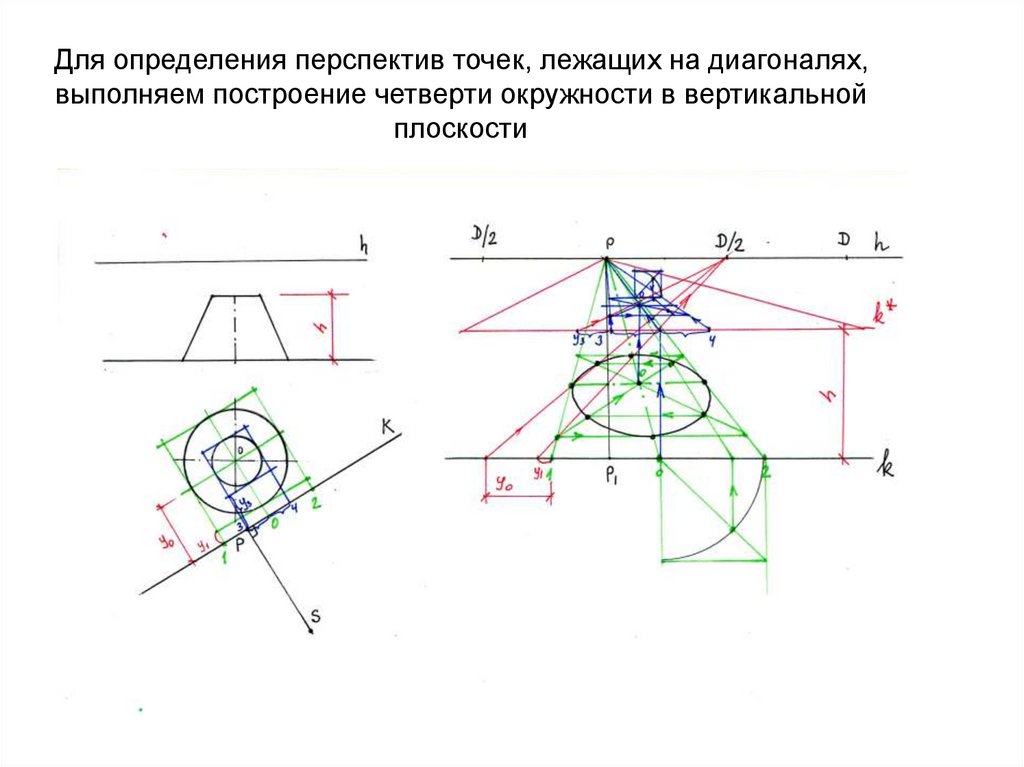
49. Перспективы точек, лежащих на диагоналях, определяем с помощью дополнительного построения четверти окружности, построенной в

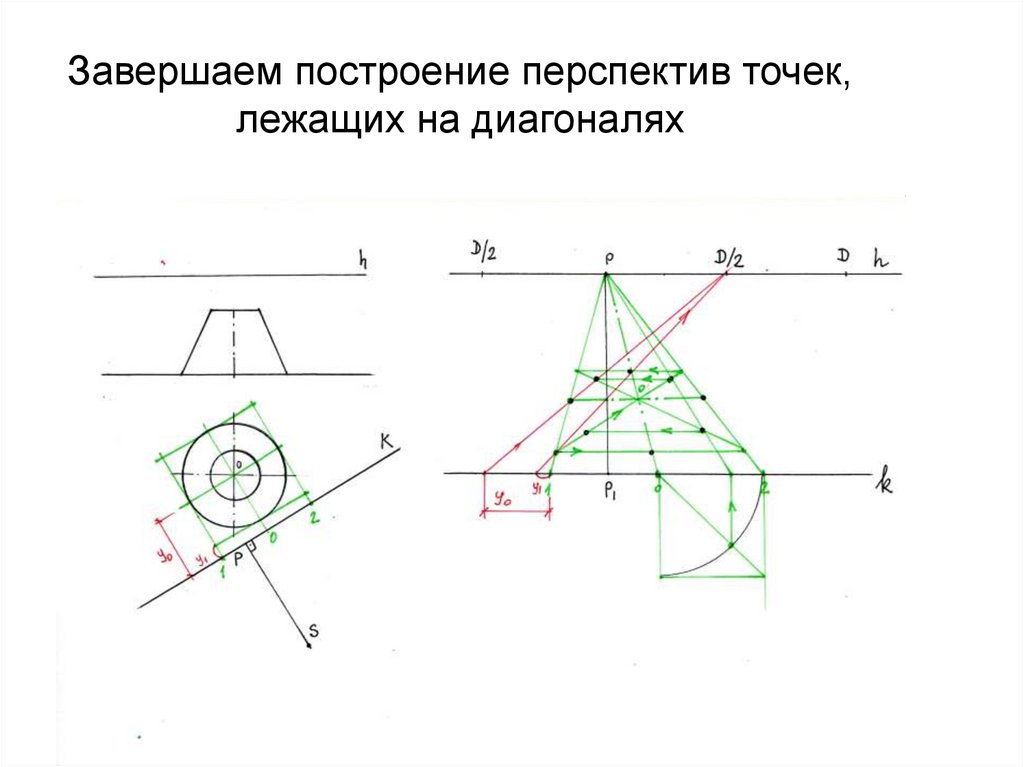
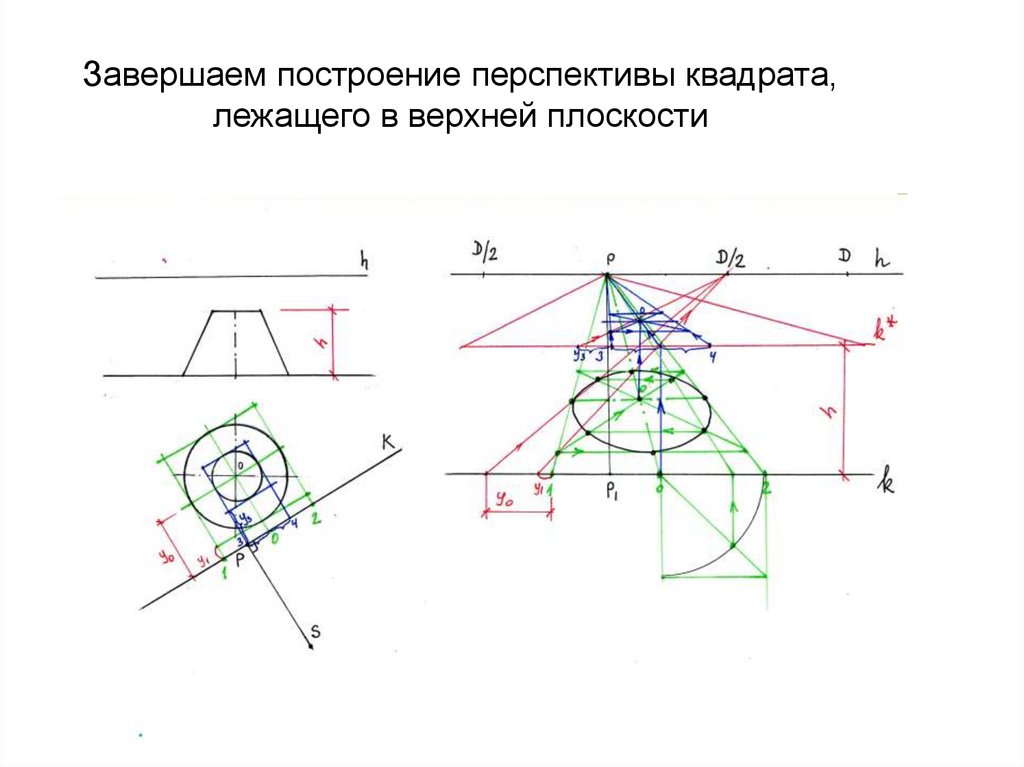
вертикальной плоскости

50. Завершаем построение перспектив точек, лежащих на диагоналях

51. Соединив все построенные точки, получим перспективу окружности

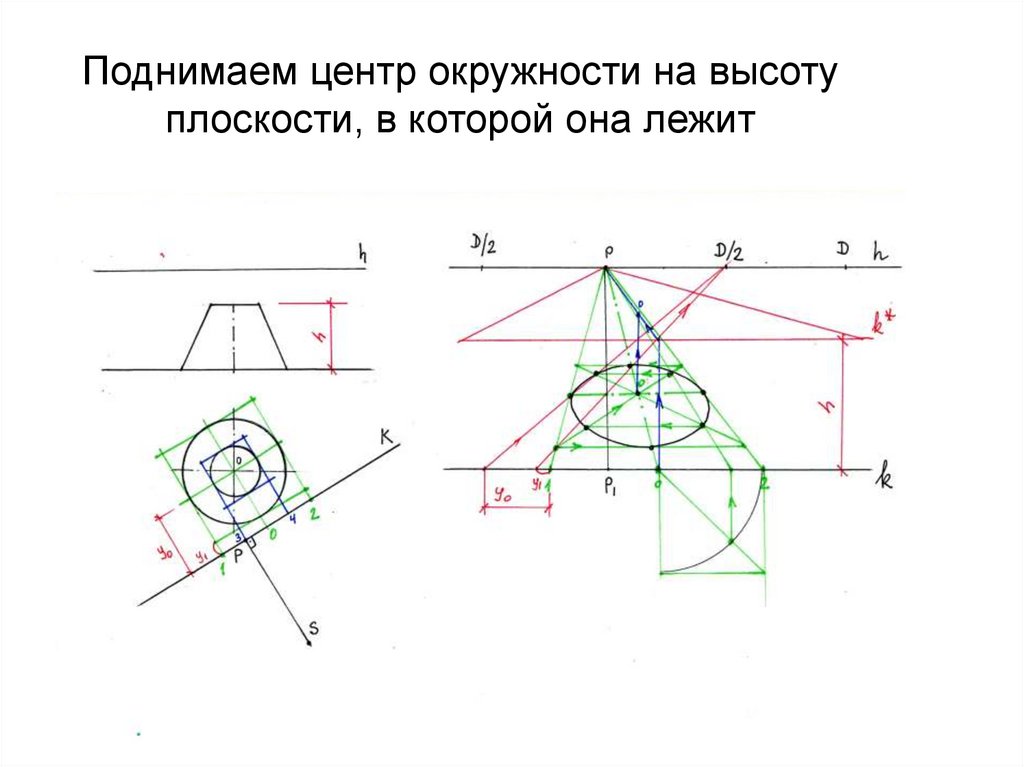
52. Для построения перспективы второй окружности в картине откладываем высоту h с учетом масштаба увеличения

53. Поднимаем центр окружности на высоту плоскости, в которой она лежит

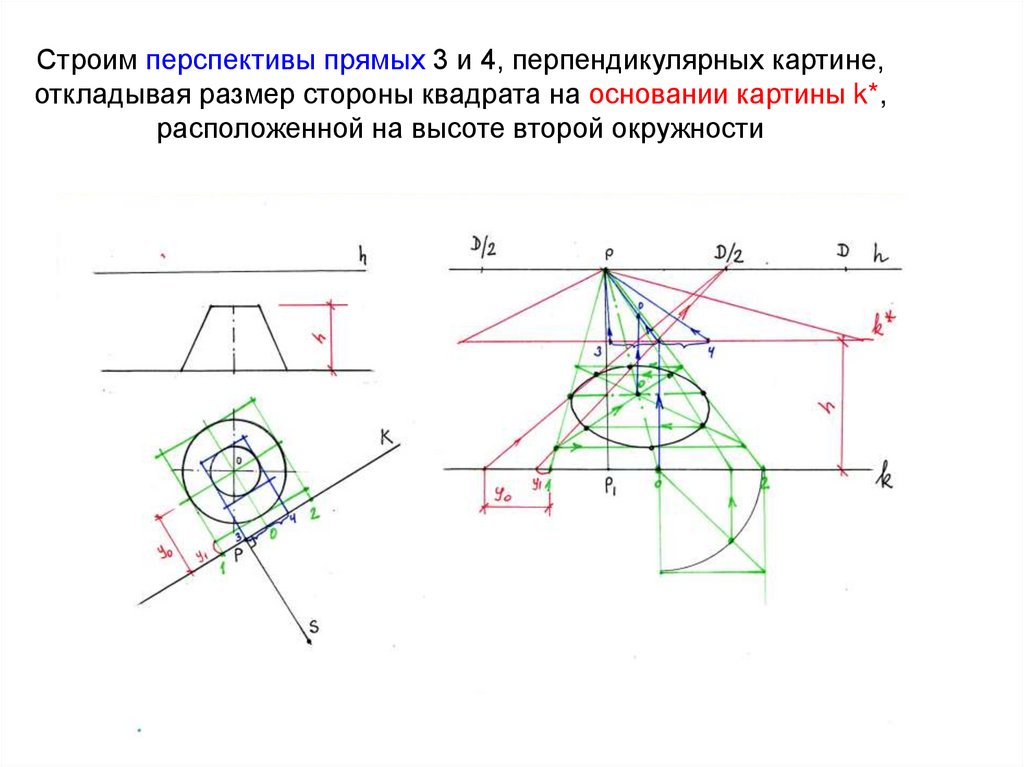
54. Строим перспективы прямых 3 и 4, перпендикулярных картине, откладывая размер стороны квадрата на основании картины k*,

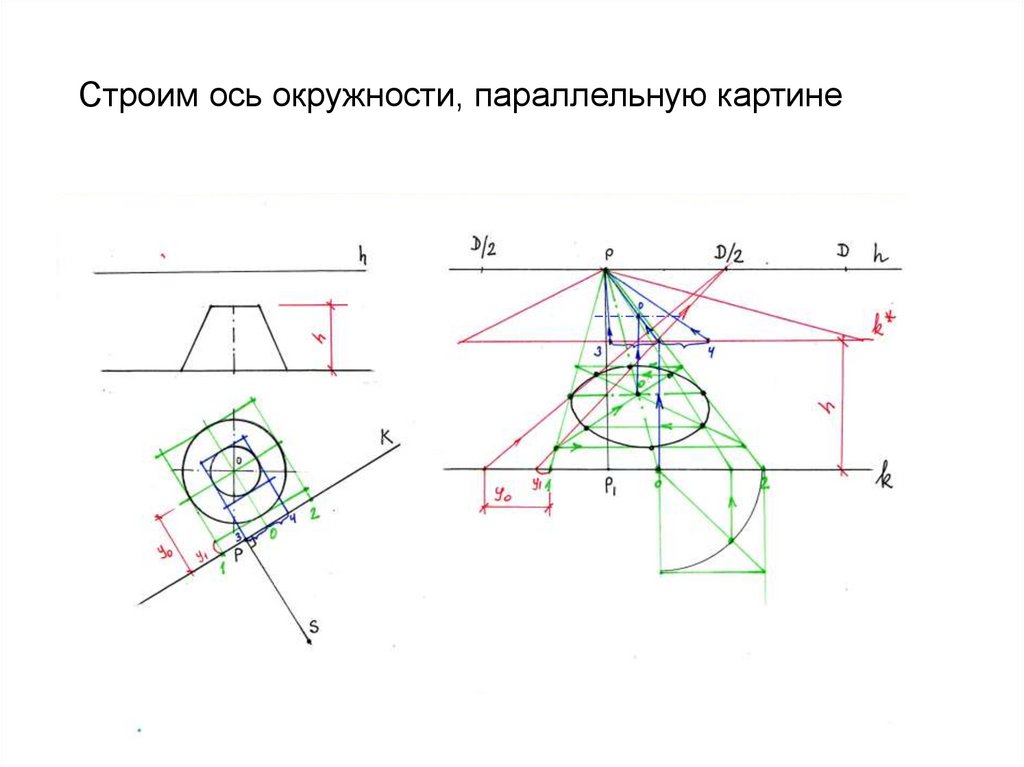
расположенной на высоте второй окружности

55. Строим ось окружности, параллельную картине

56. Определяем в перспективе положение стороны квадрата, параллельной картине и расположенной на глубине У3

Т.к. используем дробную дистанционную точку,
размер У3 откладываем на основании картины
k* без увеличения

57. Завершаем построение перспективы квадрата, лежащего в верхней плоскости

58. Для определения перспектив точек, лежащих на диагоналях, выполняем построение четверти окружности в вертикальной плоскости

59. Завершаем построение перспективы конуса, соединив касательными прямыми оба основания