Похожие презентации:
Теория функций нескольких переменных (ТФНП)
1.
Лекция 2Теория функций нескольких
переменных (ТФНП)
1. Дифференциалы высших порядков
2. Геометрические приложения ТФНП
3. Экстремумы ФНП
4. Условные экстремумы ФНП
5. Отыскание наибольшего и наименьшего
значений ФНП
2.
3.
4.
1. Дифференциалы высших порядковu f x, y
Дифференциал функции двух переменных
u
u
du ( x, y ) dx dy
x
y
du – тоже функция переменных x, y.
5.
Для этой функции тоже можно вычислитьдифференциал первого порядка .
Тогда, для исходной функции u, возникает
понятие второго дифференциала :
d u d du
2
– дифференциал второго порядка.
d u d d u
3
2
– дифференциал третьего порядка.
6.
uu
d u d (du ) d dx dy
x
y
Найдём формулу для вычисления дифференциала
второго порядка d 2u ?
2
u A
u
A
d (du ) d dx dy dx dy
y x
y
x
A
2u
2u
A x
dx
dy
2
y x
x
2
2
u
u
A y
dx
dy
2
x y
y
7.
2u2u
2u
2u
2
2
2 dx
dydx
dxdy 2 dy
x
y x
x y
y
2
2
2
u
u
u
2
2
2 dx 2
dxdy 2 dy
x
x y
y
8.
2. Геометрические приложения ТФНППрямая линия называется касательной к
поверхности в некоторой точке M(x,y,z), если
она является касательной к какой-либо
кривой, лежащей на поверхности и
проходящей через точку M.
r
n
M
L
r
a
9.
Рассмотрим поверхность Sс уравнением
F(x,y,z)=0
Если в точке M ( x, y, z ) S
F F F
0,
x y
z
или хотя бы одна из производных не
существует, то точка М называется особой
точкой поверхности S.
Если в точке M ( x, y, z ) S
все частные
производные существуют, непрерывны, и хотя
бы одна из них отлична от нуля, то точка М
называется обыкновенной точкой поверхности.
10.
Плоскость, в которой расположены всекасательные к поверхности в точке M,
называется касательной плоскостью
к
поверхности в этой точке .
Все касательные прямые к данной поверхности в
её обыкновенной точке M лежат в одной плоскости.
11.
Теорема(о существовании касательной плоскости)
Если Р0 – обыкновенная точка поверхности S, то
через эту точку можно провести касательную плоскость.
Доказательство:
Проведем через точку Р0 произвольную линию
x x(t )
L : y y (t ) r r (t )
z z (t )
L S
– вектор-функция
Вектор, направленный по касательной к линии L
имеет вид:
dr dx dy dz
, ,
dt dt dt dt
12.
13.
Подставим координаты r (t ) в уравнение поверхности:F x t , y t , z t 0
(получим тождество)
Дифференцируем по t:
F dx F dy F dz
0
x dt y dt z dt
n , dr 0
dt
- справедливо для любой точки линии L
( в частности для фиксированной точки
P0 )
14.
drn,
0,
dt
F
F
F
где n
,
,
x y z
n
перпендикулярен
касательной к L в
точке P0
Линию L выбирали произвольным образом
Вектор n перпендикулярен любой касательной
n нормальный вектор к поверхности S в точке P0
15.
Нормалью к поверхности S в точке P0называется прямая, проходящая через точку P0 ,
перпендикулярно касательной плоскости в этой
точке.
16.
Рассмотрим поверхность S с уравнением F x, y, z 0и пусть точка P0 ( x0 , y0 , z0 ) S .
F F F
nP0 , ,
- нормальный вектор к
x y z P0 поверхности S в т. Р0 .
Уравнение касательной плоскости
F
F
F
( x x0 )
( y y0 )
( z z0 ) 0
x P0
y P
z P0
0
Уравнение нормали
x x0 y y0 z z0
F
F
F
x P0
z P0
y P0
17.
3.Экстремум ФНП.
Точка P0 называется точкой локального
максимума или минимума функции u f P
если в окрестности этой точки функция
непрерывна и удовлетворяет неравенству
u ( P ) u ( P0 )
или
u ( P ) u ( P0 )
Локальные максимумы и минимумы функции
u= f(P) называют локальными экстремумами.
18.
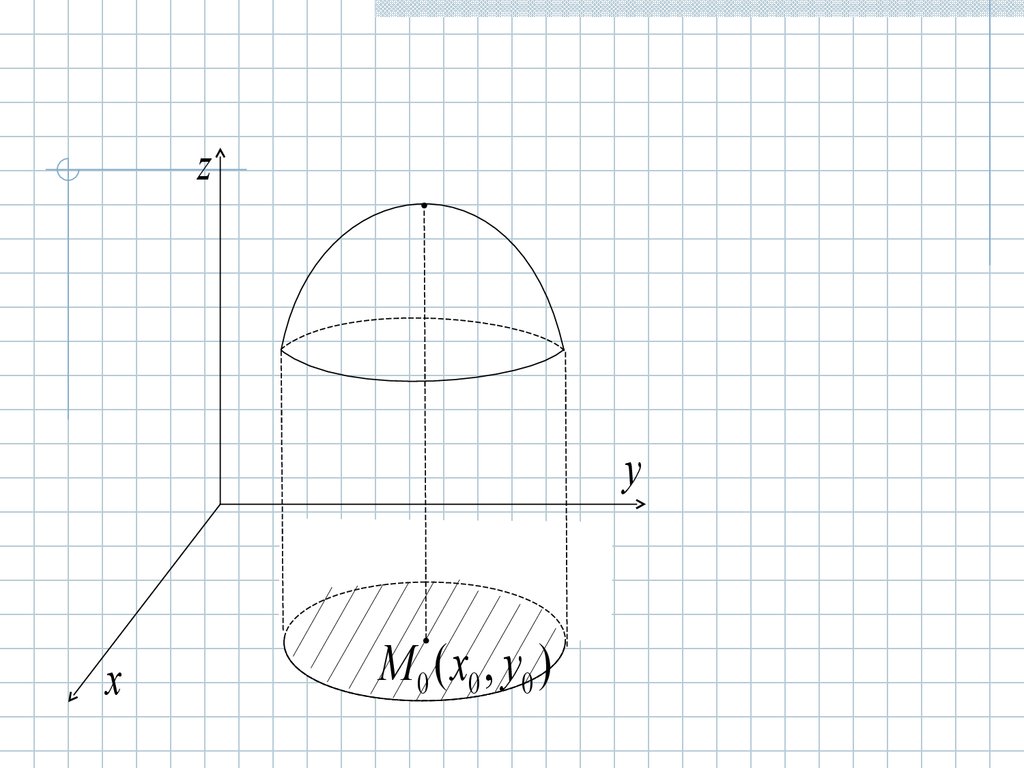
zy
x
M 0 ( x0 , y0 )
19.
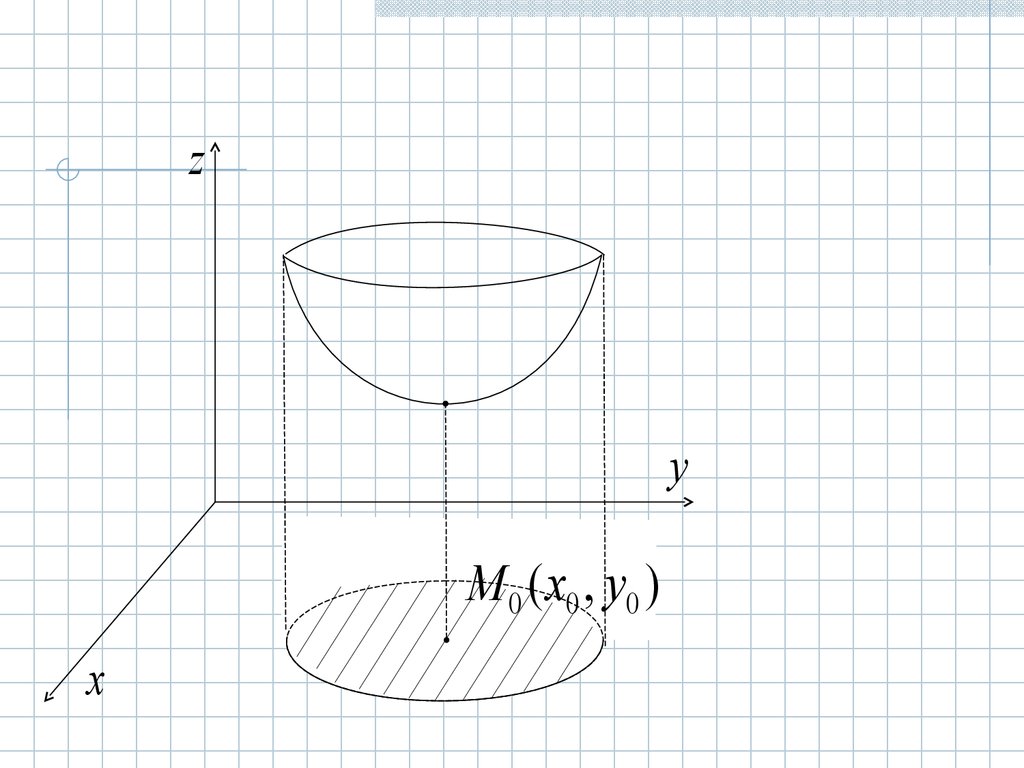
zy
M 0 ( x0 , y0 )
x
20.
Теорема (необходимое условие существования экстремума).Если
1. Р0 – точка экстремума,
2. f(P) – дифференцируемая в точке Р0
функция двух переменных,
то
частные производные первого порядка в
этой точке равны нулю
f P0
0,
x
f P0
0.
y
21.
Следствие 1Если P0 –стационарная точка функции u=f(P)
(это точка, где частные производные первого
порядка равны нулю),
то du P0 0.
Следствие 2
Точки возможного экстремума:
а) стационарные точки,
б) точки , в которых функция u=f(P) не
дифференцируема.
22.
Теорема (достаточное условие существованияэкстремума).
Если
1. Р0 – стационарная точка для u = f(P),
2. u – дважды дифференцируемая функция
в окрестности точки Р0 ,
3. вторые производные функции u=f(P)
непрерывны в точке Р0 ,
23.
то2
d
1. если u ( P0 ) 0 , то P0 - точка максимума,
2
2. если d u ( P0 ) 0 , то P0 - точка минимума,
2
если
d
u ( P0 ) не сохраняет знака при
3.
изменении знака dx , dy , то в точке P0
нет экстремума,
4. если
d 2u ( P0 ) 0
то для точки P0 требуется дополнительное
исследование.
24.
25.
4.Условные экстремумы .
На практике часто встречаются задачи об
отыскании экстремумов функции, аргументы
которой не являются независимыми переменными,
а удовлетворяют определенным условиям связи
(уравнениям).
Такие экстремумы называются условными.
26.
Постановка задачи:Пусть задана функция u=f(p) аргументы которой
связаны уравнением x, y 0 (уравнение связи)
Найти экстремумы такой функции.
Поставленная задача сводится к задаче отыскания
обычного экстремума методом Лагранжа.
27.
Определение.Функцией Лагранжа, для данной функции
u f P f ( x, y )
и уравнения связи
x, y 0 ,
называется функция L( x, y, ) f ( x, y ) ( x, y )
где
множитель Лагранжа.
28.
ТеоремаТочке ( x0 , y0 ; ) обычного экстремума функции
L( x, y; ) соответствует точка ( x0 , y0 )
условного экстремума непрерывной функции
u(P) при условии связи x, y 0 .
29.
Общая схема отыскания условного экстремума1. Поиск стационарных точек функции Лагранжа
(необходимое условие экстремума).
L
0,
x
L
0,
y
L
0
L
0,
x
L
0,
y
x, y 0.
- система уравнений для отыскания
стационарных точек ( x0 , y0 ; 0 ).
30.
2. Определение типа экстремума (достаточноеусловие экстремума).
Для установления факта наличия экстремума и
определения типа экстремума нужно исследовать
знак
2
d L( x0 , y0 ; 0 )
При этом нужно учитывать, что
dx, dy
зависят друг от друга из-за условий связи.
31.
32.
ПримерНа плоскости OXY дана фигура, ограниченная
линиями
x 0; y 0; y x 2 3 0.
Найти размеры прямоугольника, две стороны
которого совпадают с осями координат, если одна
из его вершин M(x,y) находится на параболе, а
прямоугольник вписан в эту фигуру так, чтобы
площадь прямоугольника была наибольшей.
33.
Площадь прямоугольника:f x, y S xy, f наиб . P0 P0 x0 , y0
x0 , y0 ?
Точка M принадлежит параболе,
уравнение связи
y x2 3 0
M x, y
34.
Пишем функцию Лагранжа2
L( x, y, ) xy ( y x 3)
1. Находим стационарные точки этой функции.
L
0
x
y 2 x 0
L
0 x 0
y
2
y x 3 0
L
0
x0 1
y0 2
1
0
35.
2. Определяем тип экстремума.Вычислим частные производные
2
2
L
L
L
1,
0
2
,
2
2
x
y
y
x
2
2
d L(1,2, 1) 2dx 2dxdy
2
2
y
x
3 0
Из уравнения связи
dy 2 xdx 0
находим
dy 2 xdx
При x0 1 dy 2dx
2
2
d L(1,2, 1) 6dx d 2 L(1,2, 1) 0
36.
P0 (1,2) условный максимум функции S,x0 , y0 1,2 .
37.
5. Отыскание наибольшего инаименьшего значений ФНП.
Теорема
Если функция u=f(P) дифференцируема в
ограниченной замкнутой области, то она
достигает наибольшего M (наименьшего m)
значений или в стационарной точке, или на
границе области.
38.
Схема поиска наибольшего (наименьшего) значения1. Найти стационарные точки P0 и вычислить
u f P0
2. Найти mГ и M Г наименьшее и наибольшее
значения u=f(P) на границе области
3. Выбрать
m min mГ , f P0
M max M Г , f P0
39.
Пример : найти наименьшее и наибольшее значенияx2 y2
функции u e
в области D : x 2 y 2 R 2
1. Стационарные точки
u
x2 y 2
e
2
x
0,
x
0,
0
x
u
0,0
1;
y
0
2
2
0
u
ex y
2y 0
y
40.
2. Найдем mГ и M ГR2
mГ M Г e ;
3.
m min 1, e
M max 1, e
R2
R2
1,
e
R2
.






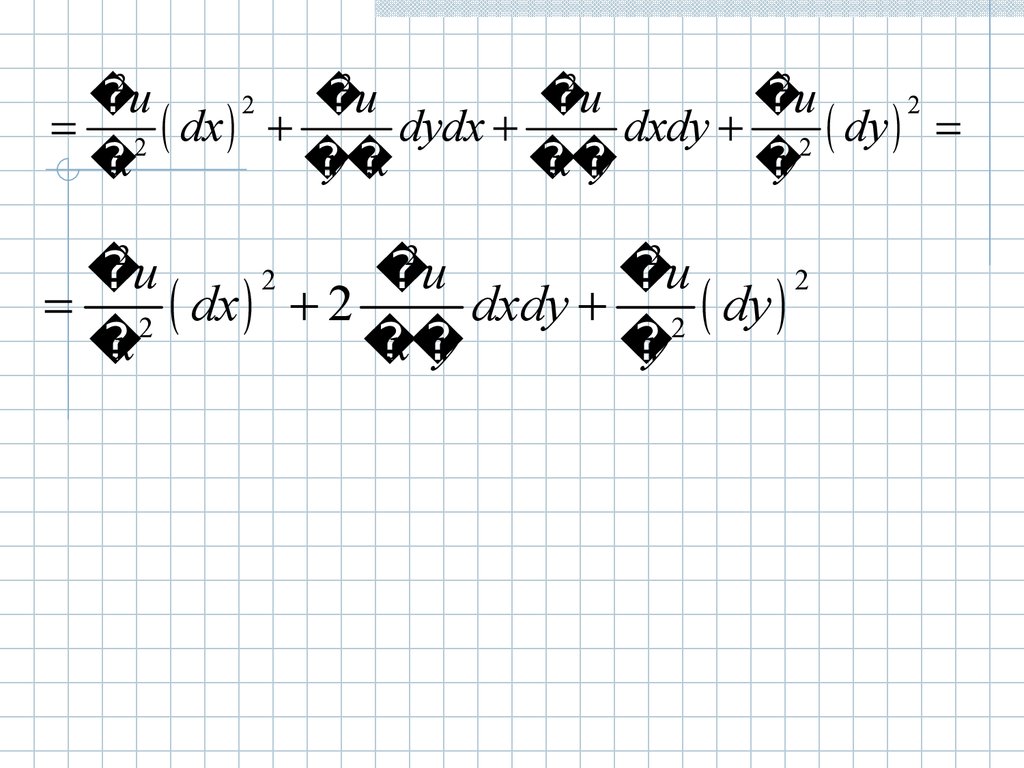





























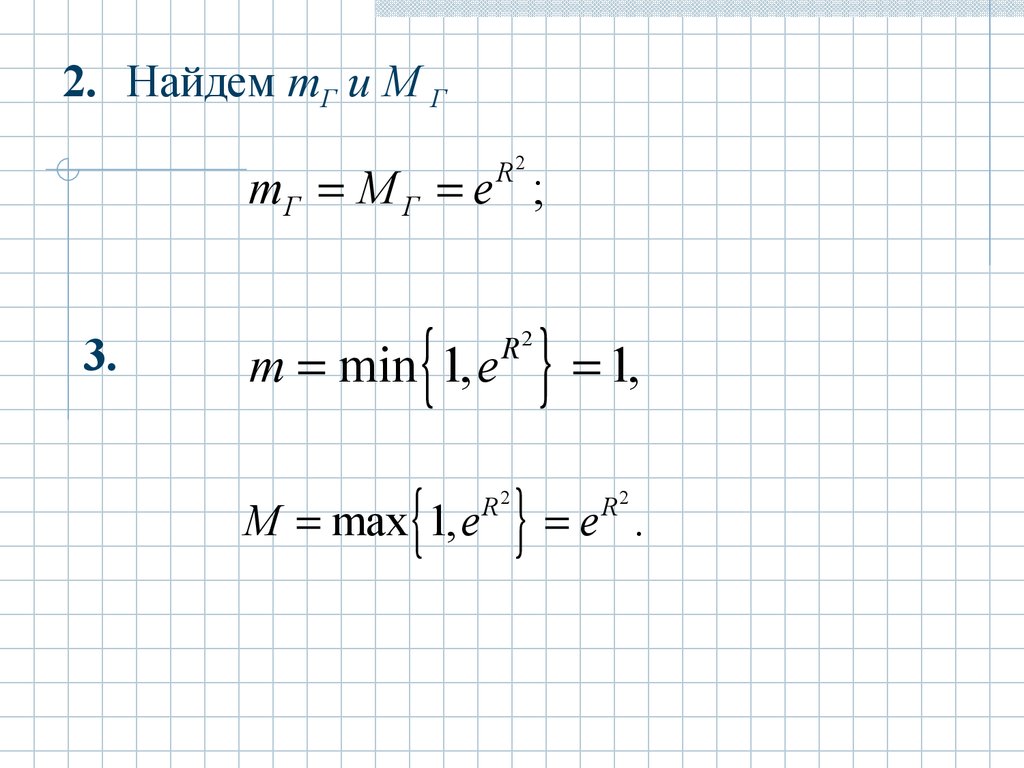
 Математика
Математика








