Механика сплошных сред

1.

Механика сплошных сред
Сплошная среда – это механическая система, в которой вещество
распределено непрерывно.
Примеры сплошных среды газ, жидкость, деформируемое твердое тело.
Силы в сплошной среде
поверхностные
объемные (массовые)

2.

Механика сплошных сред
Силы в сплошной среде
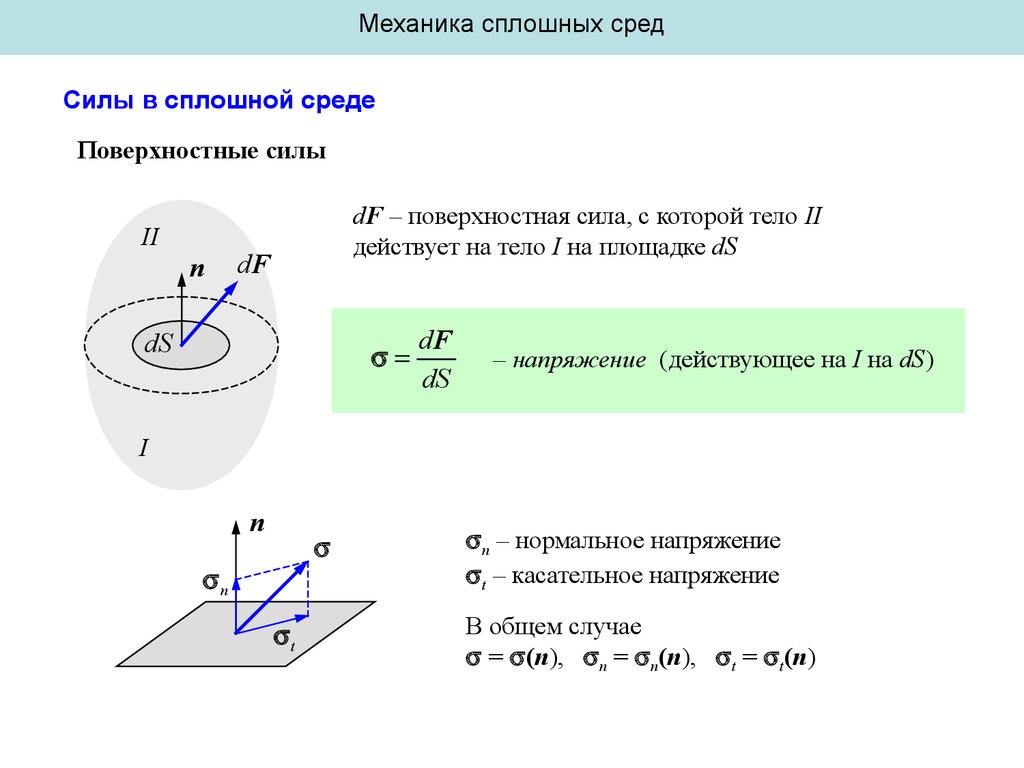
Поверхностные силы
II
n
dF – поверхностная сила, с которой тело II
действует на тело I на площадке dS
dF
dS
dF
dS
– напряжение (действующее на I на dS)
I
n
n
t
n – нормальное напряжение
t – касательное напряжение
В общем случае
= (n), n = n(n), t = t(n)

3.

Механика сплошных сред
Силы в сплошной среде
Объемные силы
dm
dF
dF – объемная сила, действующая на dm
f
Для силы тяжести f = g
dF
dm
– удельная плотность массовых сил

4.

Механика сплошных сред
Гидростатика
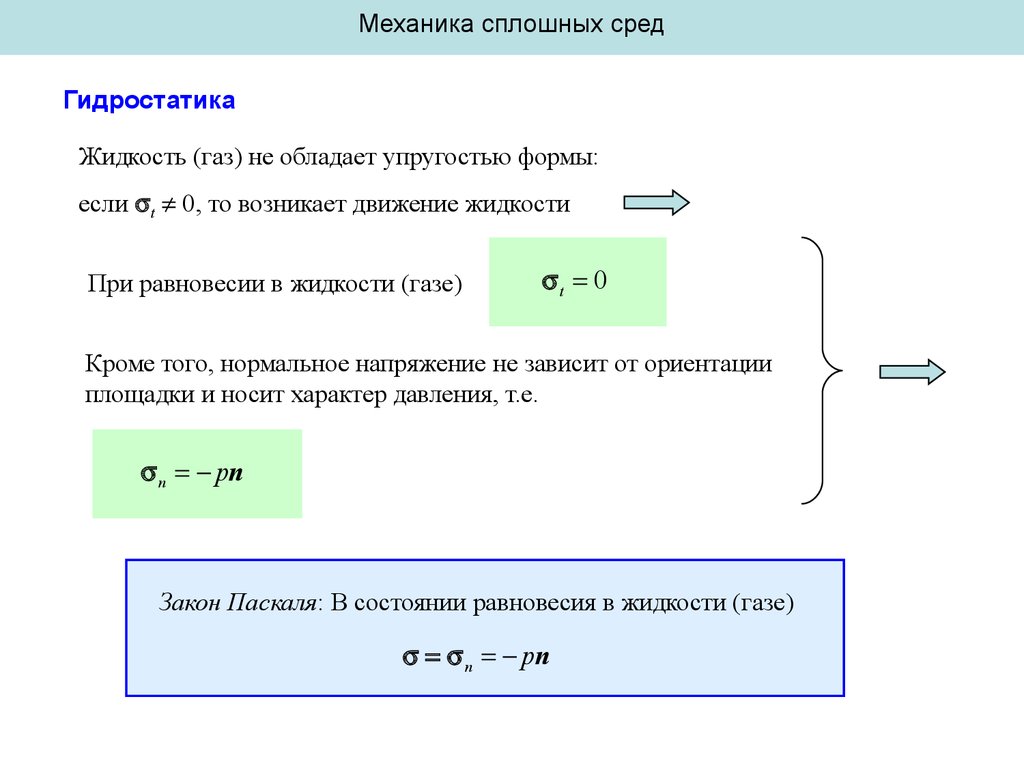
Жидкость (газ) не обладает упругостью формы:
если t 0, то возникает движение жидкости
При равновесии в жидкости (газе)
t 0
Кроме того, нормальное напряжение не зависит от ориентации
площадки и носит характер давления, т.е.
n pn
Закон Паскаля: В состоянии равновесия в жидкости (газе)
n pn

5.

Механика сплошных сред
Гидростатика
Объемная сила:
dS
dm
dFV fdm f dV
dm dV
dFV
Поверхностная сила:
dFS
dS
pdS
Согласно векторному анализу:
1
V 0 V
lim
p
p
p
p grad p i
j k
x
y
z
pn
pdS p
– градиент p (вектор)

6.

Механика сплошных сред
Гидростатика
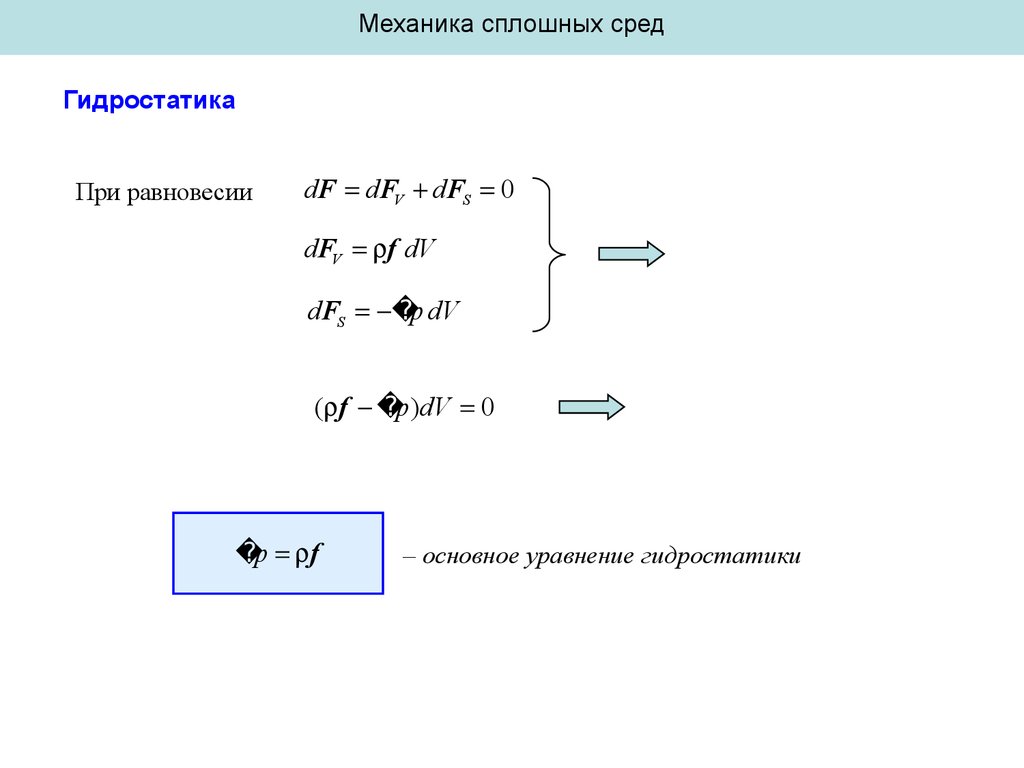
При равновесии
dF dFV dFS 0
dFV f dV
dFS p dV
( f p )dV 0
p f
– основное уравнение гидростатики

7.

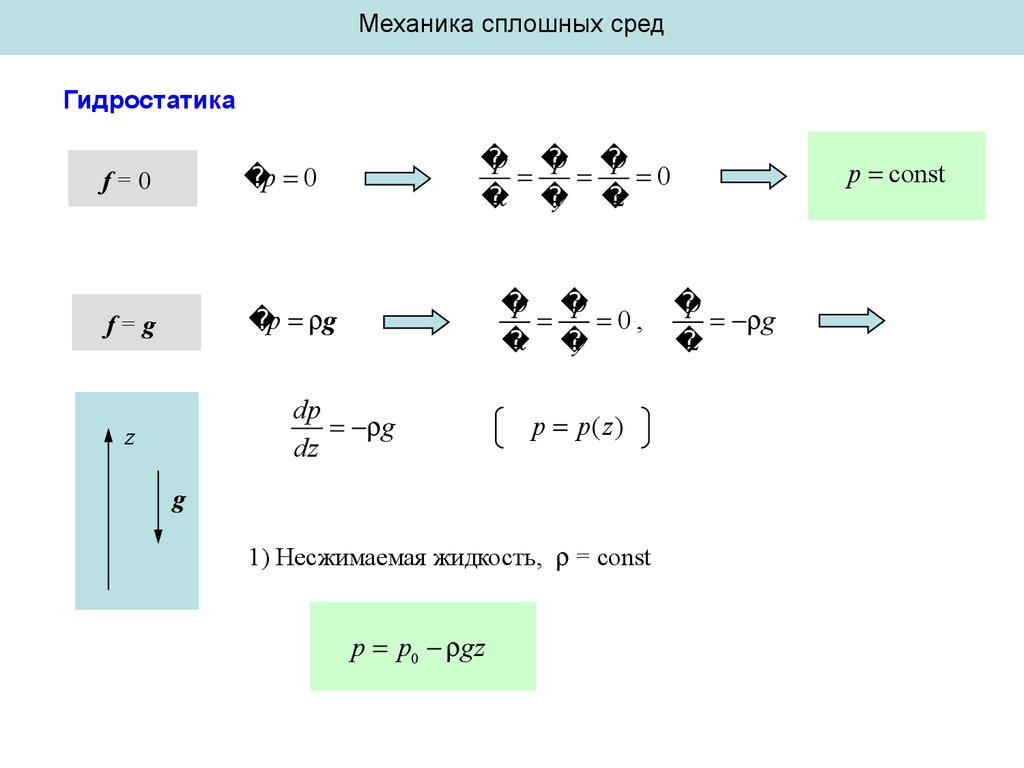
Механика сплошных сред
Гидростатика
f=0
p 0
f=g
p g
p
p
p
0
x
y
z
p
p
0,
x
y
dp
g
dz
z
p p( z )
g
1) Несжимаемая жидкость, = const
p p0 gz
p const
p
g
z

8.

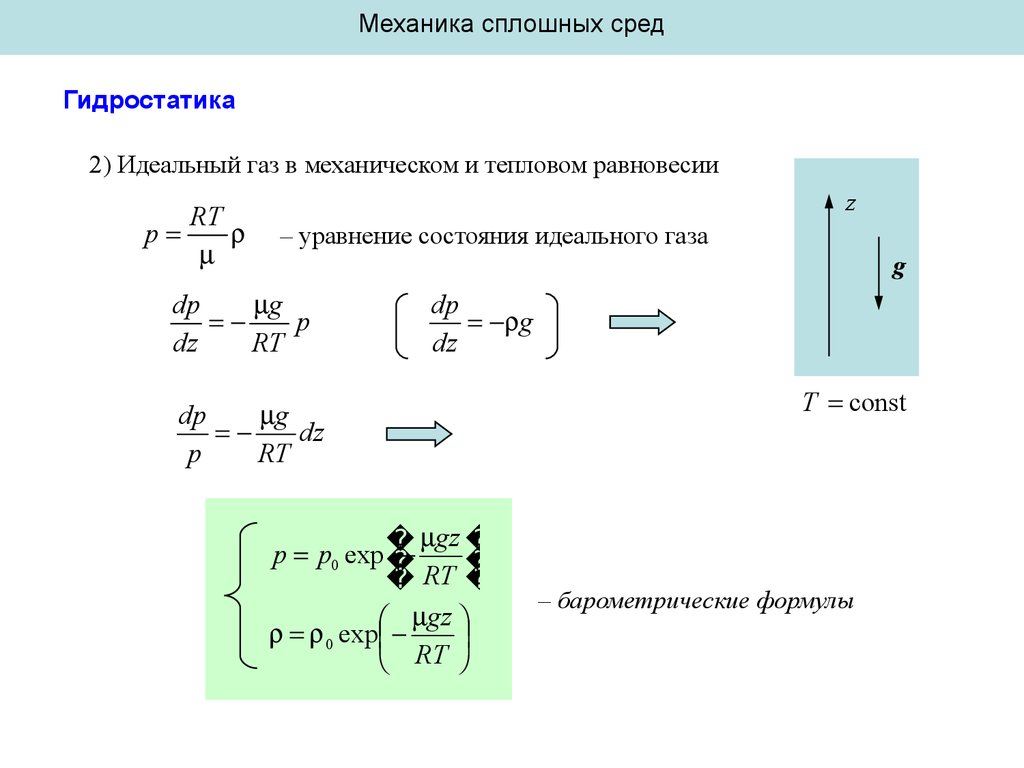
Механика сплошных сред
Гидростатика
2) Идеальный газ в механическом и тепловом равновесии
RT
p
z
– уравнение состояния идеального газа
g
dp
g
p
dz
RT
dp
g
dz
dp
g
dz
p
RT
gz
p p0 exp
RT
gz
0 exp
RT
T const
– барометрические формулы

9.

Механика сплошных сред
Гидростатика
Закон Архимеда
m
FA
FA – равнодействующая сил давления,
P' – сила тяжести (вес) жидкого объема,
P – сила тяжести (вес) тела
При равновесии жидкого объема FA = P'.
P
m
g
m
FA
P mg
Такая же по величине выталкивающая сила
(сила Архимеда) действует и на тело.
Закон Архимеда:
Выталкивающая сила, действующая на
неподвижное тело в жидкости, равна весу
вытесненной жидкости, направлена вверх и
проходит через центр масс.

10.

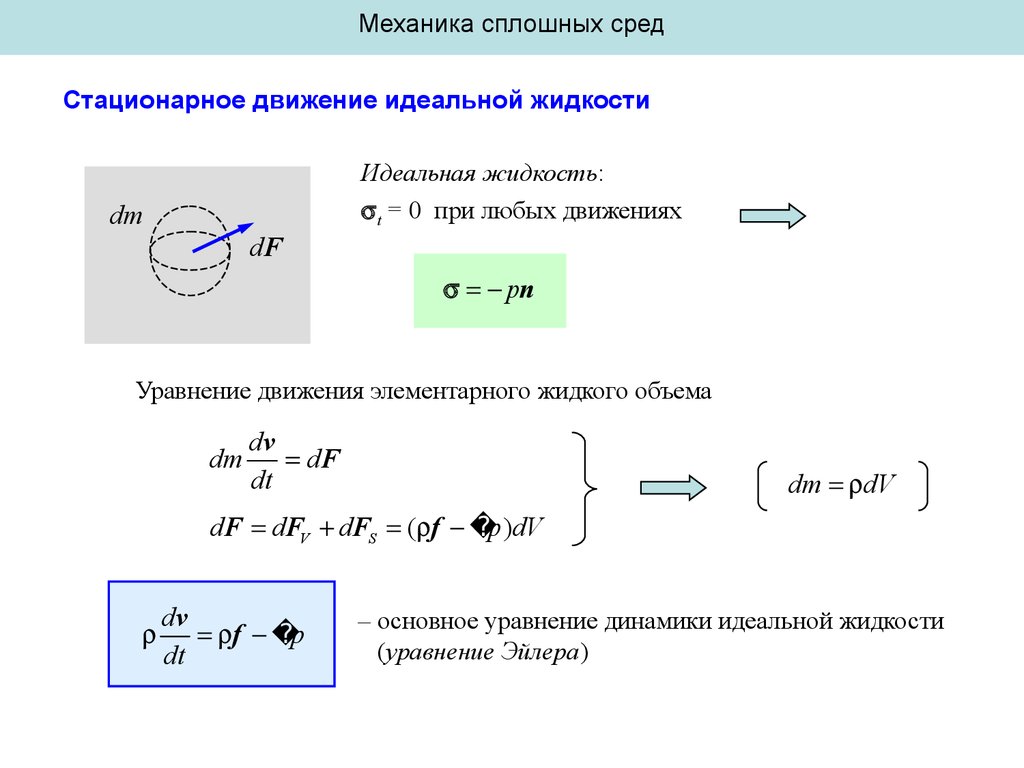
Механика сплошных сред
Стационарное движение идеальной жидкости
Идеальная жидкость:
t = 0 при любых движениях
dm
dF
pn
Уравнение движения элементарного жидкого объема
dm
dv
dF
dt
dm dV
dF dFV dFS ( f p )dV
dv
f p
dt
– основное уравнение динамики идеальной жидкости
(уравнение Эйлера)

11.

Механика сплошных сред
Стационарное движение идеальной жидкости
Трубка тока – трубчатая поверхность, образованная линиями тока
dm
dm
B
B'
D
D'
p2 , 2
p1 , 1
S1
S2
A'
A
l1
C
C'
l2
При движении ABCD → A'B'C'D'
dA p1S1l1 p2 S2l2
dm 1 S1l1 2 S 2 l 2
p p
dA 1 2
dm
1 2

12.

Механика сплошных сред
Стационарное движение идеальной жидкости
dE
dm
– удельная плотность энергии (E – полная энергия)
Изменение энергии трубки тока ABCD
dE ( 2 1 )dm
В соответствии с законом сохранения энергии
1
p1
p
2 2
1
2
p
const (L)
dE dA
или (на линии тока)
– уравнение Бернулли

13.

Механика сплошных сред
Стационарное движение идеальной жидкости
В случае = const и f = g
(Uвн = const по причине несжимаемости)
v2
p
gh const (L)
2
Истечение жидкости из сосуда
0
линия
тока
v2
gh
2
– уравнение Бернулли
0
1
p0
p0 v 2
gh
2
h
v 2 gh
1
v
– формула Торричелли

14.

Механика сплошных сред
Вязкая жидкость
v
F
Fтр
h
Fтр
F
Для поддержания движения
верхней пластины и удержания в
покое нижней требуется
приложить постоянную силу F.
S
Опыт:
v
h
1)
F S
2)
жидкость прилипает к пластинкам
, где µ – коэффициент (динамической) вязкости
Поэтому в формуле можно считать
1) v – относительная скорость граничных слоев жидкости
2) F – приложена к этим граничным слоям

15.

Механика сплошных сред
Вязкая жидкость
y
F
y
V
v v
V – прямоугольный объем,
боковые грани которого
параллельны потоку
v
F
F S
t
dFt
v
dS
n
n – нормаль к dS
v
v
S
y
y

16.

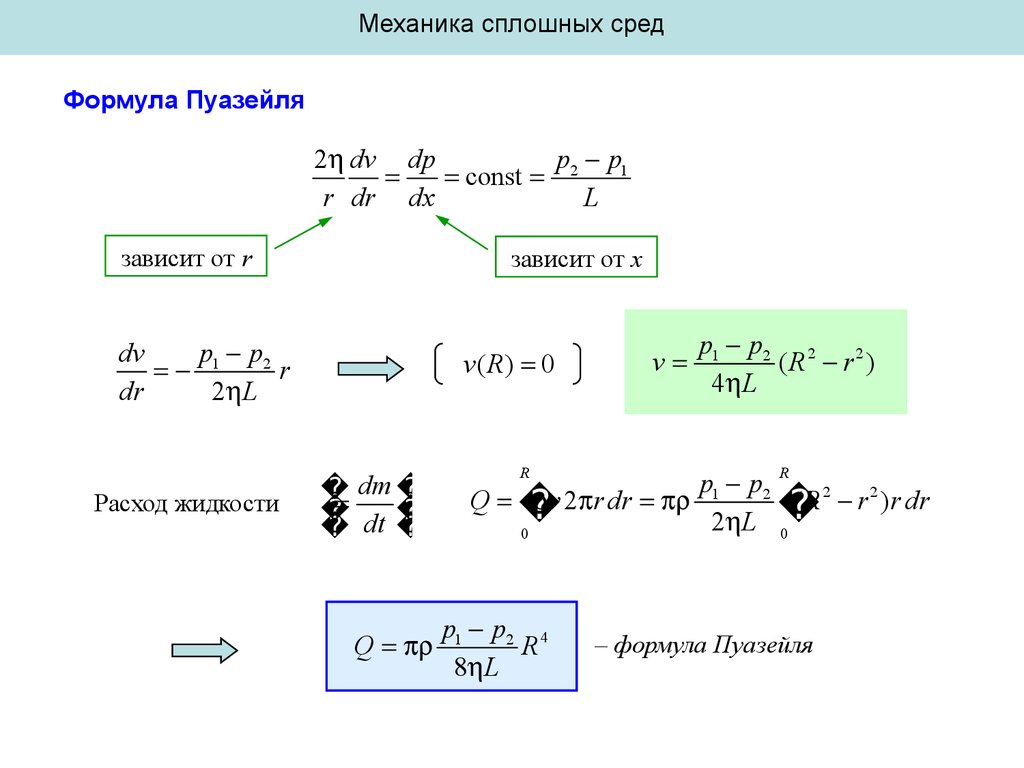
Механика сплошных сред
Формула Пуазейля
L
R
p1
dFтр
p( x )
p ( x dx )
r
x
dx
Положим, что линии тока ║ оси трубы и p p ( x ), v v ( r )
Движение стационарное
F 0
r 2 p( x ) p( x dx ) (2 r
dx )
i
dv
0
dr
на цилиндрик
r 2dx
p2

17.

Механика сплошных сред
Формула Пуазейля
2 dv dp
p p1
const 2
r dr dx
L
зависит от r
зависит от x
dv
p p2
1
r
dr
2 L
Расход жидкости
v( R) 0
dm
dt
Q
R
v
p1 p2 2 2
(R r )
4 L
R
p p2
2
2
Q
v 2 r dr 1
(
R
r
)r dr
2 L 0
0
p1 p2 4
R
8 L
– формула Пуазейля

18.

Механика сплошных сред
Идеально упругие тела
Деформации
упругие
пластические
Упругие деформации – это деформации, исчезающие после прекращения
действия деформирующих тело сил.
При пластических деформациях после прекращения действия внешних сил
деформации полностью не исчезают.
Идеально упругих тела – это тела, деформации в которых пропорциональны
внутренним напряжениям и для них справедлив принцип суперпозиции:
деформация тела, вызываемая действием нескольких сил, равна сумме
деформаций, вызываемой каждой силой в отдельности.
Т.е. идеально упругие тела подчиняются закону Гука.

19.

Механика сплошных сред
Идеально упругие тела
F
По закону Гука:
l
S
d
d
1)
F
l
E
S
l
E – модуль Юнга
l
2)
d
l
d
l
– коэффициент Пуассона
Модуль Юнга E и коэффициент Пуассона полностью определяют
упругие свойства изотропного материала.

20.

Механика сплошных сред
Идеально упругие тела
Кубик
В отсутствии деформации
a1
a1 a2 a3 a
При малых деформациях
a2
a3
V ( a1a2 a3 ) a1 a2 a3
V
a1a2a3
a1
a2
a3

21.

Механика сплошных сред
Идеально упругие тела
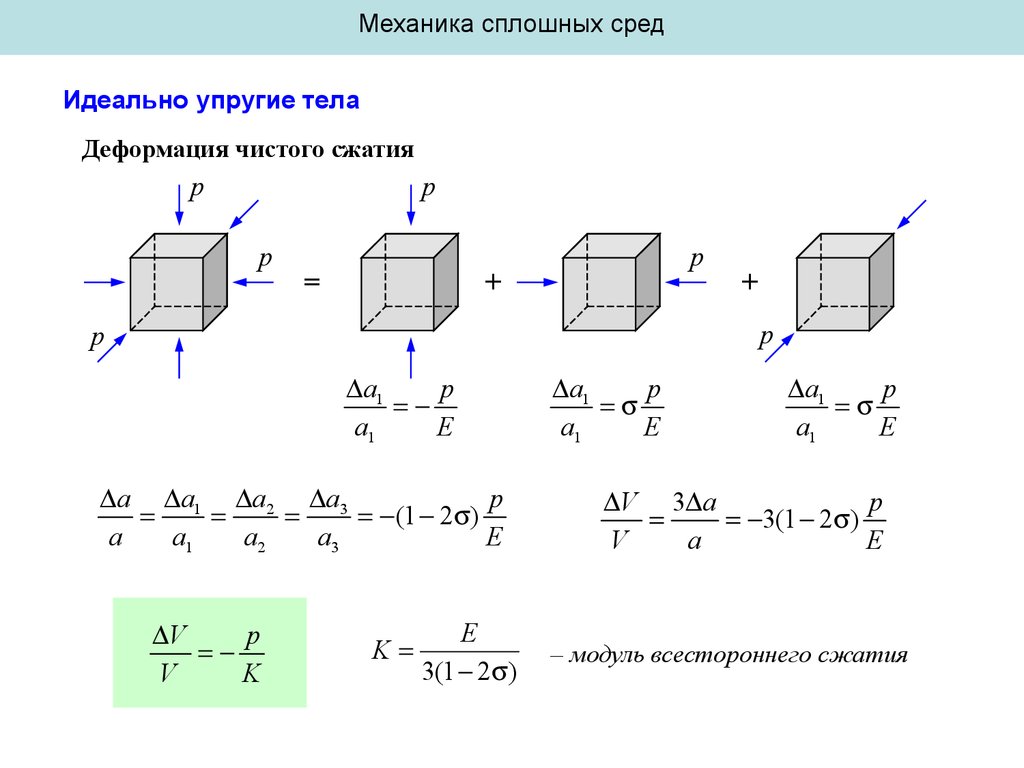
Деформация чистого сжатия
p
p
p
=
p
+
+
p
p
a1
p
a1
E
a a1 a2 a3
p
(1 2 )
a
a1
a2
a3
E
V
p
V
K
K
E
3(1 2 )
a1
p
a1
E
a1
p
a1
E
V 3 a
p
3(1 2 )
V
a
E
– модуль всестороннего сжатия

22.

Механика сплошных сред
Идеально упругие тела
Деформация чистого сдвига
=
+
a1
a1
E
a1
a1
E
a1
(1 )
a1
E
a 2
a
1
a2
a1
a3
0
a3
V
0
V

23.

Механика сплошных сред
Идеально упругие тела
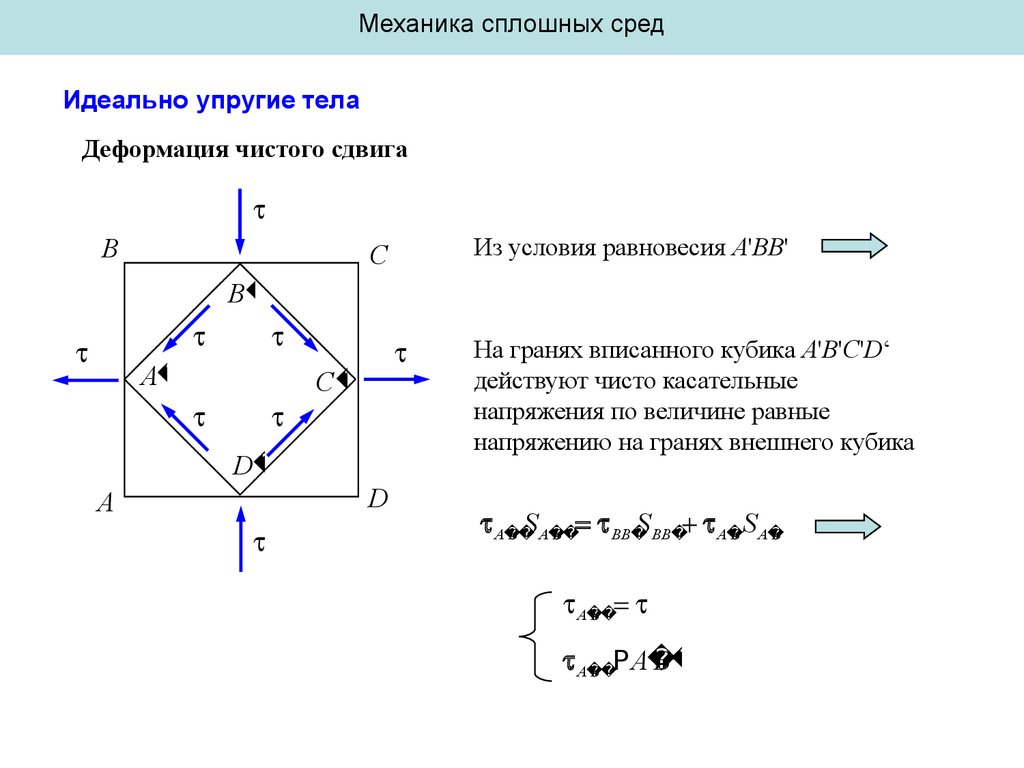
Деформация чистого сдвига
B
Из условия равновесия A'BB'
C
B
A
C
D
D
A
На гранях вписанного кубика A'B'C'D‘
действуют чисто касательные
напряжения по величине равные
напряжению на гранях внешнего кубика
A
S BB A B S A B
B S A
B BB
A
B
A
B PA B

24.

Механика сплошных сред
Идеально упругие тела
Деформация чистого сдвига
Переход от деформации чистого сдвига к деформации сжатие–растяжение
Чистый сдвиг
Сжатие–растяжение

25.

Механика сплошных сред
Идеально упругие тела
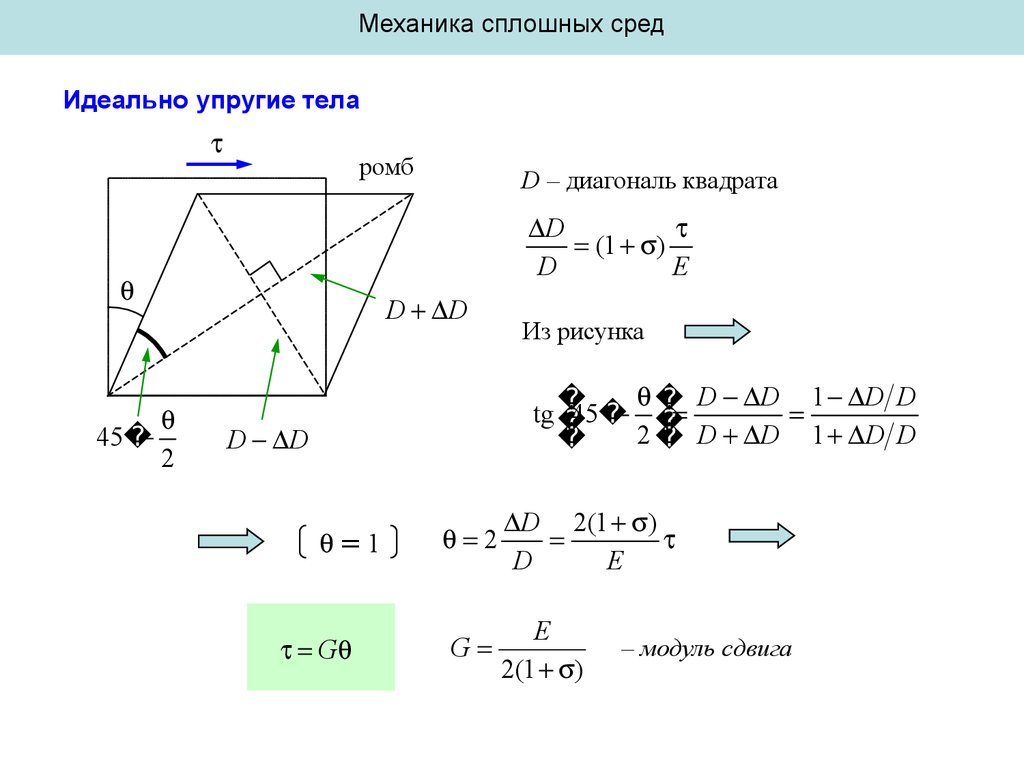
ромб
D
(1 )
D
E
45
D – диагональ квадрата
D D
2
Из рисунка
D D 1 D D
tg
45
2
D
D
1 D D
D D
=1
G
2
D 2(1 )
D
E
G
E
2(1 )
– модуль сдвига