Плоское потенциальное движение. Использование вихревой теории в расчетах турбомашин

1. ГИДРОМЕХАНИКА

2.

Лекция 11
Плоское потенциальное
движение

3.

Использование вихревой теории в расчетах
турбомашин
Следовательно, можно считать,
что поток имеет равные скорости и давления во всех точках
любой описанной из центра колеса окружности и результирующее усилие на лопатку колеса
равно нулю, колесо не создает
давления.
Однако в действительности при конечном числе
лопаток давление с передней (лобовой) стороны
лопатки должно быть выше, чем с задней стороны,
причем именно благодаря этой разности давлений
турбомашина может, сообщать жидкости энергию.

4.

Использование вихревой теории в расчетах
турбомашин
Таким образом, неточность струйной теории заключается не в каком-нибудь второстепенном обстоятельстве, а в самом существе вопроса.
Рабочее колесо передает жидкости некоторый вращательный момент, и на отдельных элементах лопатки имеют место разности давлений. Это создает
различные по величине относительные скорости в
канале между лопатками.

5.

Использование вихревой теории в расчетах
турбомашин
Относительный поток в каналах колеса не только не
является струйным, но имеет вихревой характер.

6.

Использование вихревой теории в расчетах
турбомашин
При обтекании тела потоком возникают силы воздействия жидкости на тело. Характер обтекания получается одинаковым, независимо от того, движется ли
тело, а жидкость неподвижна или наоборот.
Рассмотрим обтекание плоской пластинки потоком
при движении ее под углом 90° к потоку.
Струя а, направленная
нa центр пластинки, по
мере приближения к
пластинке теpяет свою
скорость
При этом по закону Бернулли увеличивается
давление потока. Соседние струи увеличенным
давлением оттесняются к краям пластинки, где
происходит сужение потока, скорости возрастают и
давление падает. Таким образом, наибольшее
давление поток производит в точке 1 и наименьшее
– в точке 4.

7.

Использование вихревой теории в расчетах
турбомашин
За пластинкой жидкость, стремясь заполнить область
пониженного давления, движется в направлении обратном основному потоку, создавая так называемые
возвратные токи в, образуются вихри.
Чем больше вихреобразование, тем сильнее разрежение. Плоская пластинка является плохо обтекаемой формой.
Возникшая разность давлений создает силу, направленную в сторону, обратную движению пластинки.
Эта сила называется силой сопротивления.
Из теоремы импульсов получается формула, по которой определяется
величина силы сопротивления:
2
Fсопр С
и
2
С – коэффициент, зависящий
от формы тела

8.

Использование вихревой теории в расчетах
турбомашин
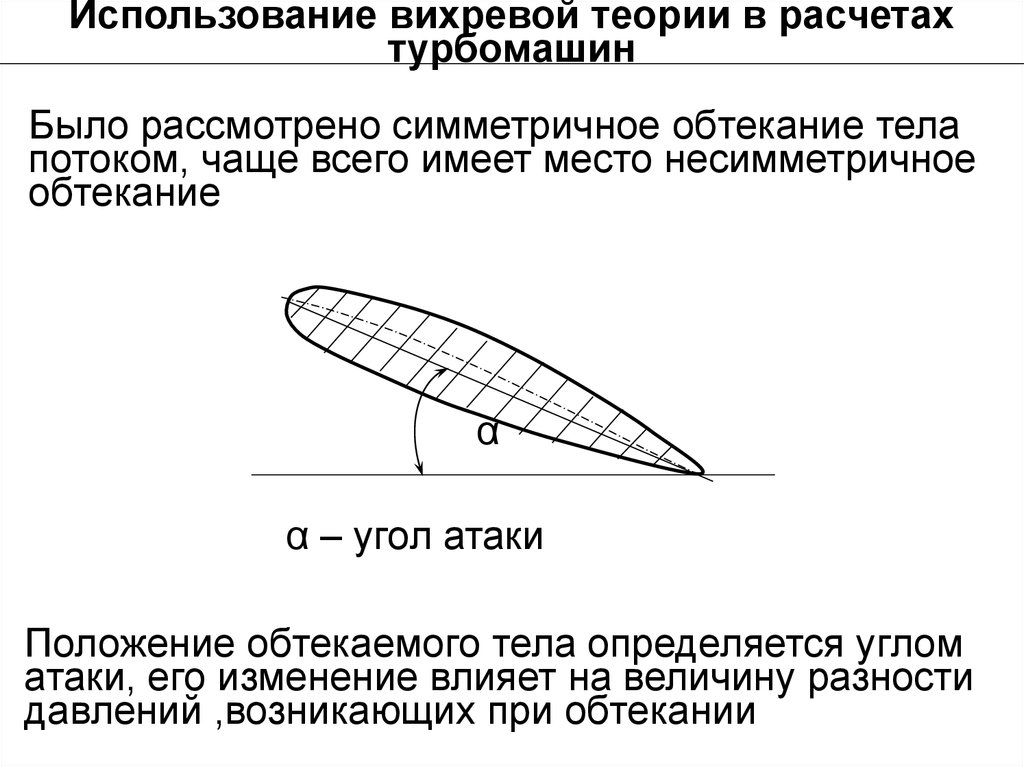
Было рассмотрено симметричное обтекание тела
потоком, чаще всего имеет место несимметричное
обтекание
α
α – угол атаки
Положение обтекаемого тела определяется углом
атаки, его изменение влияет на величину разности
давлений ,возникающих при обтекании

9.

Использование вихревой теории в расчетах
турбомашин
Его изменение влияет на величину разности давлений,возникающих при обтекании.
1 – точка с максимальным давлением, 2 – с наименьшим
Наибольшее давление будет в т.1. Однако в отличие
от симметричного обтекания точка 1 смещена от
центра в сторону ребра атаки.

10.

Использование вихревой теории в расчетах
турбомашин
При обтекании верхней части профиля, вследствие
его выпуклости, происходит сужение струй, увеличение скорости и уменьшение давления. Наименьшее
давление будет в т. 2.
Ниже точки 2 имеет место вихреобразование, вызываемое трением потока о поверхность.

11.

Использование вихревой теории в расчетах
турбомашин
Очевидно, что в основном все элементы, определяющие действие силы сопротивления при несимметричном обтекании (косом ударе ), т. е. ее величина,
направление и точка приложения, зависят от угла
атаки и формы профиля (тела). Поэтому каждому
углу атаки данного профиля соответствует свой
коэффициент, обозначаемый Сα.
Fсопр С
и
2
2
Сα – коэффициент, зависящий
от формы тела и угла атаки

12.

Теорема Жуковского для решетки профилей
Теорема Жуковского была опубликована в 1906 году
и сыграла выдающуюся роль в развитии теории крыла и стала основой теории летательных аппаратов,
Теорема получила также широкое применение в
теории гребных винтов кораблей, теории лопастных
гидравлических и газовых турбомашин.
Ее значение определяется тем, что она вскрывает
физическую причину появления подъемной силы,
при которой являются вихри. Мерой интенсивности
последних является циркуляция скорости.
При этом несущественна причина, порождающая вихри. Для идеальной жидкости циркуляция обусловлена
течением плоского вихря.

13.

Теорема Жуковского для решетки профилей
Такие вихри, определяющие величину подъемной
силы, Жуковский называл присоединенными.
В реальной жидкости циркуляция порождается
действием сил трения, которые развиваются и
проявляются в пограничном слое, т. е. присоединенные вихри – это теоретический эквивалент
системы вихрей, возникающих в пограничном слое
реальной жидкости, вследствие вязкости.
Окончательно вопрос о расчете величины подъемной
силы решил постулат Чаплыгина-Жуковского, устранивший неопределенность величины циркуляции для
крыловых профилей.

14.

Теорема Жуковского для решетки профилей
Бесконечная совокупность одинаковых крыловых
профилей, одинаково ориентированных и
расположенных с постоянным шагом вдоль прямой,
называется плоской гидродинамической решеткой.
Если мы рассечем все лопатки колеса осевой турбомашины двумя цилиндрическими поверхностями,
проведенными из центрa колеса на малом расстоянии друг от друга, и одну из этих цилиндрических
поверхностей развернем в плоскость, то получим
решетку профилей или крыльев.

15.

Теорема Жуковского для решетки профилей
d
u2x
p2
p1
b
t
c
Плоская решетка профилей омывается потоком
несжимаемой жидкости,
плотность которой равна ρ
а
u1y
u2y
u1x
Проведем в потоке
контур abcd, где линии bc и ad – отрезки
линий тока, а длина
отрезков ab и cd равна
шaгy решетки t.
и1, р1 - скорость и давление невозмущенного
потока перед решеткой;
и2, р2 –соответственные величины за ней

16.

Теорема Жуковского для решетки профилей
Так как течение плоское, расчеты ведутся для
единицы ширины профиля
Пусть поток перед решеткой и за ней однородный.
Тогда из условия постоянства расхода жидкости Q
через решетку, его величину
Q=u1xt= u2xt
откуда
u1x= u2x= ux
Напишем для контура abcd уравнение количества
движения
mu1 – mu2= R1+R2+Fпр = R1+R2-Fпот
Масса в единицу времени определится как массовый
расход: m= ρQ= ρuхt , тогда
ρuхtu1 – ρuхtu2= R1+R2-Fпот

17.

Теорема Жуковского для решетки профилей
R - силы давления; силы давления, приложенные к
отрезкам bc и ad, считаем равными по величине и
противоположно направленными, т. е. их действие
уравновешено.
Fпр-- сила, действующая со стороны профиля на
поток; Fпот – сила, c которой поток действует на
профиль. Они равны по величине и противоположно
направлены.
Запишем уравнение в проекциях на оси координат
ось х
t(ρuх2 –ρuх2)= р1t – р2t -Fпотх
t(ρuх2 –ρuх2)= t (р1 – р2) -Fпотх
0
Fпотх= t (р1 – р2)

18.

Теорема Жуковского для решетки профилей
ось у
t(ρuхu2у –ρuх u1у)= -Fпоту
t ρuх(u2у –u1у)= -Fпоту
Fпотх= t (р1 – р2)
Fпоту=t ρuх(u1у –u2у)
Выразим разность давлений из уравнения Бернулли
для идеальной жидкости
и12
и22
p1
p2
2
2
и22 и12 2
2
p1 p2
(и2 и1 )
2
2
2

19.

Теорема Жуковского для решетки профилей
Так как скорость можно выразить через проекции
и 2 и х2 и 2у ,
то уравнение можно представить в виде
2
2
2
p1 p2 (и2 и1 ) (и2 х и22 у и12х и12у )
2
2
2
2
p1 p2 (и2 у и1 у ) (и2 у и1 у )(и2 у и1 у )
2
2
Обратимся к циркуляции по замкнутому контуру abcd.
При этом части контурного интеграла, соответствующие обходу участков линий тока bc и da взаимно
уничтожаются, так как значения скоростей в соответственных точках этих участков одинаковы, а направления обхода противоположны.

20.

Теорема Жуковского для решетки профилей
Поэтому в результате циркуляция будет выражена
обходом по частям ab и cd, скорости противоположны
а расстояния равны t:
Г (и2 у и1 у )t
Заменим одну скобку в формуле циркуляцией
p1 p2 Г (и2 у и1 у )
2t
Учитывая полученное соотношение, подставим это
в выражение для горизонтальной проекции силы, с
которой поток воздействует на профиль решетки
Fпотх= t (р1 – р2)
Fпот х
Г (и2 у и1 у )
2

21.

Теорема Жуковского для решетки профилей
Вертикальная составляющая силы будет равна
Fпоту=t ρuх(u1у –u2у)
Fпот у и х Г,
Результирующая сила
Fпот Г (
и 2 у и1 у
2
) 2 и х2 ,
Рассмотрим множитель, представленный в виде
корня

22.

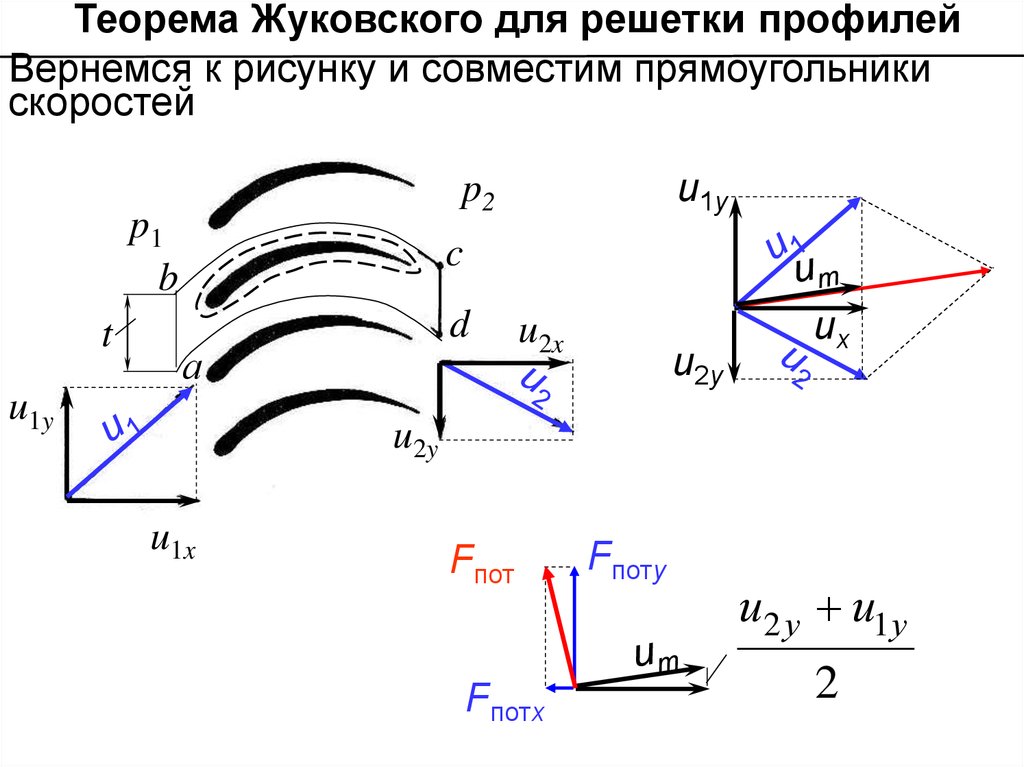
Теорема Жуковского для решетки профилей
Вернемся к рисунку и совместим прямоугольники
скоростей
p1
b
t
u1y
p2
c
d
а
u1y
u2x
u2y
ux
u2y
u1x
Fпот
Fпотх
Fпоту
и2 у и1 у
2

23.

Теорема Жуковского для решетки профилей
Из сложения скоростей видно, что скорость иm – это
половина суммы скоростей до и после решетки, или
средняя скорость обтекания решетки,
иm (
Тогда
и 2 у и1 у
2
)
2
2
их
Fпот Ги m
Формула выражает теорему Жуковского для
профиля в плоской решетке.

24.

Теорема Жуковского для решетки профилей
Однако наличия только такой связи недостаточно
для вычисления подъемной силы единичного
профиля или решетки профилей, так как значение
циркуляции остается неизвестным. Необходимо
иметь еще условие, определяющее величину циркуляции. Это условие, как уже отмечалось, было
доказано Н. Е. Жуковским и С. А. Чаплыгиным в 1909
г. и называется постулатом Жуковского – Чаплыгина.
Это условие формулируется так: при безотрывном
обтекании профиля вокруг него возникает циркуляция Г такой величины, при которой задняя острая
кромка является точкой схода струй.

25.

Теорема Жуковского для решетки профилей
Результирующую силу можно разложить на составляющие по осям, проведенным по направлению подъемной силы и перпендикулярно ему.
Fпот
Fпот
Fпоту
Fпоту
Fпотх
Fпотх
Fсопр

26.

Теорема Жуковского для решетки профилей
В соответствии с возникновением силы лобового сопротивления при обтекании тел , направленной навстречу движению, определим проекцию силы на направление скорости в виде:
Fсопр С х А
2
и0
2
А lb - площадь, равная произведению размаха
крыла l на хорду профиля b;
Сх- коэффициент лобового сопротивления.

27.

Теорема Жуковского для решетки профилей
Также и подъемную силу можно выразить в виде
Fпод С у А
2
и0
2
Су- коэффициент подъемной силы.
Коэффициенты Сх и Су определяют экспериментально.

28.

Анализ работы турбомашины по вихревой теории
Лопатка рабочего колеса турбомашины представляет собой слегка изогнутое тело, подобное крылу.
Акад. Г. Ф. Проскура на основе вихревой теории крыла проф. Н. Е. Жуковского создал вихревую теорию
турбомашин
Рабочий процесс в турбомашине по этой теории протекает следующим образом: при вращении ротора
турбомашины за счет динамического воздействия на
жидкость лопаток колеса, обтекаемых потоком, появляются гидроаэродинамические силы, создающие
приращение полного напора, необходимого для перемещения потока во внешней сети турбоустановки.

29.

Анализ работы турбомашины по вихревой теории
Эти силы связаны с циркуляцией абсолютной
скорости с по замкнутому
круговому контуру.
В рабочем колесе центробежной машины циркуляция по контуру, охватываюшему лопатки, называется внешней циркуляцией
Г2. Циркуляция по контуру,
не охватывающему лопатки, называется внутренней
циркуляuией Г1.

30.

Анализ работы турбомашины по вихревой теории
Если эти величины определять по окружности радиусов r2 и r1, то
Г2=2πr2с2и
Г1=2πr1с1и
откуда
r2 c2u
Г2
2
Г2
r2с2и
2
Г1
r1с1и
2
Г1
r1c1u
2
Если учесть определение окружной скорости, то
формулу теоретического напора

31.

Анализ работы турбомашины по вихревой теории
можно выразить
H т (r2c2u r1c1u )
g
или
Hт
(Г 2 Г1 )
2 g
Так как внешняя и внутренняя циркуляция различны,
то между этими областями должны находиться
вихри, которые создают циркуляцию.
Таким образом, наличие циркуляции в каналах
между лопатками вытекает из существа вихревой
теории. Это же явление наблюдается и на опытах.
Циркуляция по какому-либо контуру равняется сумме
циркуляций по замкнутым линиям, заключенным
внутри рассматриваемого контура.
Г2=Г1+zГs
Г2-Г1=zГs

32.

Анализ работы турбомашины по вихревой теории
Тогда
zГ s
Hт
2 g
Вихревая теория не включает для турбомашин новых принципов, но внесенное изменение дает
возможность для конечного числа лопаток ввести
поправки к элементарной теории с помощью коэффициента напора, который учитывает все потери
давления и подачи.

33.

ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
Турбомашины обладают тем свойством, что их подача, давление, скорость вращения и конструктивные
размеры рабочих органов находятся в определенной
зависимости.
Количество жидкости, которое пройдет через рабочее колесо турбомашины в единицу времени, т. е. его
подачу, можно определить, пользуясь уравнени-ем
расхода:
Q=ωc,
где ω- площадь живого сечения потока, м2;
с - средняя скорость жидкости, нормальная к
этому сечению, м/сек.

34.

ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
У центробежных машин площадь выходного живого
сечения рабочего колеса без учета стеснения его
лопатками, определяется как боковая поверхность
цилиндра, диаметр которого равен внешнему диаметру колеса D2, а выcoтa его равна ширине колеса b2, т
е.
ω = π D2 b 2 .
Средней скоростью, нормальной к этой поверхности,
будет проекция абсолютной скорости с2 на направление радиуса, т. е.
с2r = с2sinα2
Скорость с2r называется радиальной или меридиональной.

35.

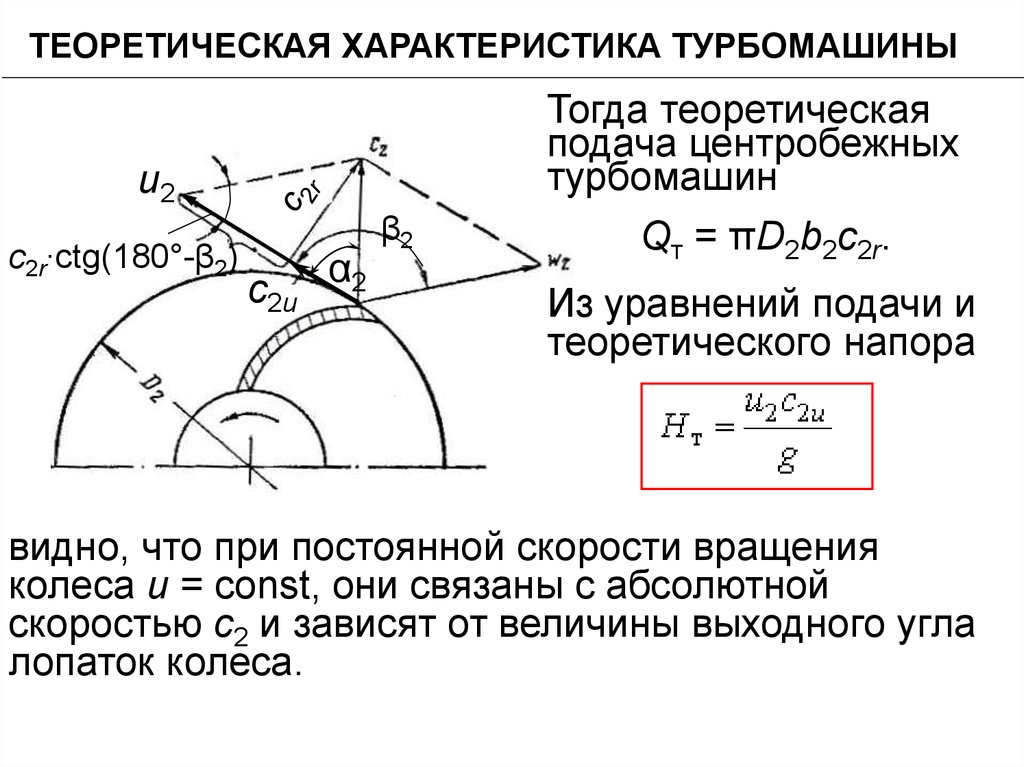
ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
Тогда теоретическая
подача центробежных
турбомашин
u2
с2r∙ctg(180°-β2)
с2u
α2
β2
Qт = πD2b2с2r.
Из уравнений подачи и
теоретического напора
видно, что при постоянной скорости вращения
колеса u = const, они связаны с абсолютной
скоростью c2 и зависят от величины выходного угла
лопаток колеса.

36.

ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
Чтобы выразить скорость с2и через Qт надо
выразить ее из параллелограмма скоростей на
выходе из рабочего колеса
с2и = и2 - с2r ctg (180°-β2)
180°-β2
u2
с2r∙ctg(180°-β2)
с2u
α2
β2
или
с2и = и2 +с2r ctgβ2
с2 r
Qт
D2b2
Qт
с2и = и2 +ctgβ2
D2b2

37.

ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
Подставляя это значение в формулу теоретического
напора, получим уравнение теоретической характеристики турбомашины
и2
Qт
Н т (и 2 сtg 2
)
g
D2b2
и 2 сtg 2
Нт
Qт
g
g D2b2
2
и2
Уравнение выражает зависимость давления от
подачи для одноколесной турбомашины.

38.

ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
Уравнение содержит переменные величин в первой
степени. Поэтому, если построить в координатах
«подача – напор» график по уравнению, получится
прямая, зависящая от угла β2