Одномерные временные ряды

1. Тема 4: Одномерные временные ряды

Временной ряд – эконометрическая
модель, которая строится по временным
данным (в отличие от пространственных).
Временной ряд (ряд динамики) –
последовательность значений показателя
у, упорядоченных по значениям
переменной t (по времени)
уt – уровень ряда
1

2.

Величина каждого уровня складывается
под влиянием различных факторов,
которые можно разбить на 3 группы:
• факторы, формирующие тенденцию ряда
f (t )
• факторы, формирующие циклические
(периодические) колебания c(t )
• случайные факторы t
Как правило, уровень ряда содержит
все эти компоненты
2

3. Модель временного ряда

• Аддитивная модель:
yt f (t ) c(t ) t
• Мультипликативная модель:
yt f (t ) c(t ) t
Задача: определение наличия
и количественная оценка
каждой составляющей
3

4. Автокорреляция уровней временного ряда

Автокорреляция – корреляционная
зависимость между последовательными
уровнями ряда
ryt yt 1 r1 – коэффициент
автокорреляции 1-го порядка (лаг = 1):
n
r1
( yt y1 )( yt 1 y2 )
t 2
n
n
( yt y1 ) ( yt 1 y2 )
t 2
2
t 2
2
4

5.

ry y r2
t
t 2
– коэффициент автокорреляции
2-го порядка (лаг = 2):
n
r2
( yt y3 )( yt 2 y4 )
t 3
n
n
( yt y3 ) ( yt 2 y4 )
2
t 3
2
t 3
1 n
y3
yt
n 2 t 3
r
1 n
y4
yt 2
n 2 t 3
k
Совокупность k различных порядков
называется автокорреляционной функцией
временного ряда. Её график – коррелограмма.5

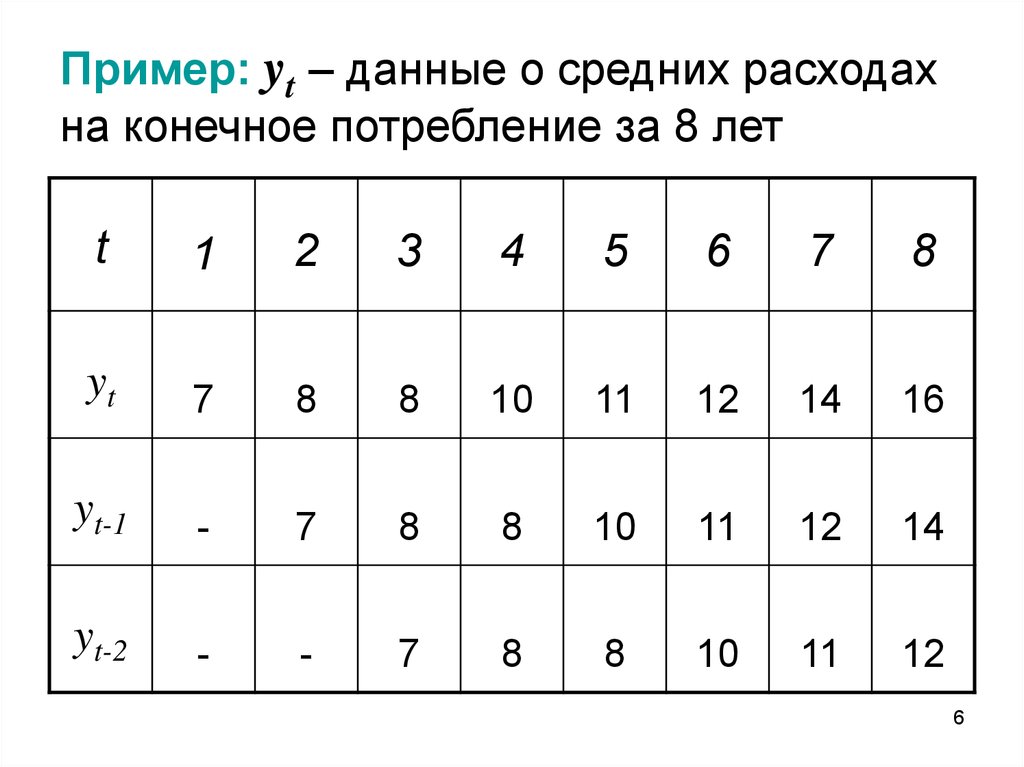
6. Пример: yt – данные о средних расходах на конечное потребление за 8 лет

t
1
2
3
4
5
6
7
8
yt
7
8
8
10
11
12
14
16
yt-1
-
7
8
8
10
11
12
14
yt-2
-
-
7
8
8
10
11
12
6

7. Определение структуры временного ряда

• Высокое значение r1 свидетельствует о
наличии линейной тенденции. При
увеличении лага связь ослабевает
• Если r1 – наиболее высокий коэффициент, то ряд содержит только тенденцию (линейную)
• Если наиболее высокий коэффициент –
rm , то ряд содержит циклические
колебания с периодом m
7

8.

• Если нет статистически значимых коэффициентов, то:
– либо ряд не содержит тенденции и
циклических колебаний, т. е. включает
только случайную составляющую t
(стационарный ряд);
– либо ряд содержит сильную нелинейную
тенденцию
8

9. Моделирование тенденции временного ряда

Метод – аналитическое выравнивание
(определение функции f (t ) ) с помощью
МНК.
Определение типа тенденции:
• построение и визуальный анализ графика
• расчёт и анализ показателей динамики
• расчёт и анализ коэффициентов автокорреляции исходных и преобразованных
уровней
9

10. Наиболее распространённые функции трендов:

yˆt b0 b1 t yˆt b0 b1 t b2 t
yˆt b0 b1 / t
yˆt e
b0 b1 t
yˆ b0 t
b1
L
yˆt
b b t
1 e
0
1
10
2

11.

Если ряд содержит нелинейную
тенденцию, то выбор наилучшего
уравнения тренда производится
методом перебора
на основе критерия максимума
скорректированного индекса
детерминации R2adj
(либо минимума стандартной ошибки
оценки Sст.)
11

12. Моделирование ряда с циклическими (сезонными) колебаниями

Тип модели выбирается в зависимости от
характера колебаний:
• если амплитуды колебаний примерно
одинаковы, используется аддитивная
модель временного ряда;
• если амплитуды увеличиваются или
уменьшаются, используется мультипликативная модель
12

13. Алгоритм определения сезонной составляющей:

1. Выравнивание исходного ряда методом
скользящей средней (у*) по интервалу,
равному периоду колебаний (это
устраняет сезонную компоненту c(t))
2. Расчёт значений c(t)
для аддитивной модели:
для мультипликативной
модели:
c(t ) yt
c(t ) yt /
*
yt
*
yt
и их усреднение по годам.
13

14. Алгоритм определения сезонной составляющей:

3. Устранение сезонной компоненты из
исходных данных:
• для аддитивной модели: yt c (t ) f (t ) t
для мультипликативной
модели:
yt / c (t ) f (t ) t
4. Определение тенденции – расчёт
5. Расчёт прогнозных значений:
пр
yˆt
fˆпр (t ) c (t )
пр
yˆt
fˆ (t )
fˆпр (t ) c (t )
14

15. Расчёт и анализ ошибок

• Абсолютные ошибки:
yˆt fˆ (t ) c (t ) или
t yt yˆt
yˆ fˆ (t ) c (t )
t
• Относительные ошибки:
t yt
fˆ (t ) c (t )
Отношение суммы квадратов абсолютных ошибок к общей сумме квадратов
отклонений характеризует стандартную
ошибку оценки аддитивной модели
15