Похожие презентации:
Анализ временных рядов
1. Анализ временных рядов
2. Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени.
Временной ряд – это совокупность значенийкакого-либо показателя за
несколько последовательных моментов
или периодов времени.
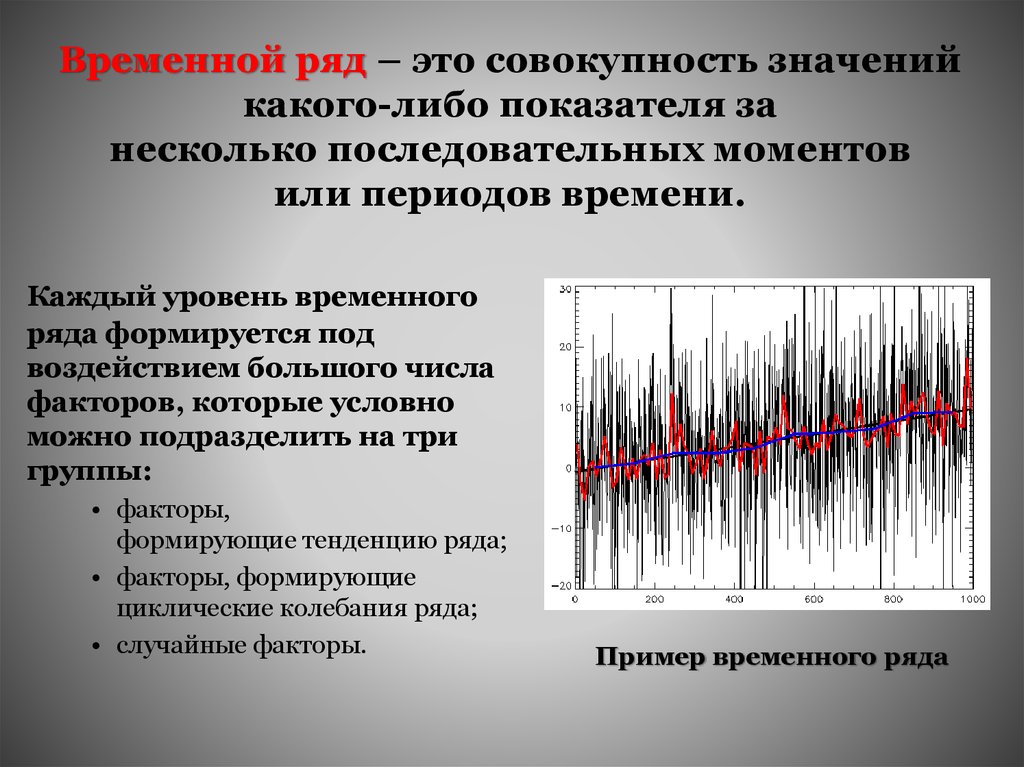
Каждый уровень временного
ряда формируется под
воздействием большого числа
факторов, которые условно
можно подразделить на три
группы:
• факторы,
формирующие тенденцию ряда;
• факторы, формирующие
циклические колебания ряда;
• случайные факторы.
Пример временного ряда
3. Классификация временных рядов
1. по времени - моментные и интервальные.Интервальный ряд: ряды показателей
объема продукции предприятия по месяцам
года, количества отработанных человеко-дней
по отдельным периодам
Моментный ряд: последовательность показателей
численности населения на начало года, поголовье
скота в фермерских хозяйствах на 1 декабря или 1
июня за несколько лет, величина запаса какого-либо
материала на начало периода
2. по форме представления уровней:
ряды абсолютных , относительных и средних величин ;
3. по расстоянию между датами или интервалами времени:
полные и неполные временные ряды.
Полные ряды имеют место, когда даты регистрации или окончания периодов следуют друг за другом с
равными интервалами, неполные - когда принцип равных интервалов не соблюдается.
4. по содержанию показателей - ряды частных и агрегированных
показателей.
Частные показатели: среднесуточный объем
выпуска промышленной продукции, численность
граждан, состоящих на учете в службе занятости;
эффективность социальной политики государства;
остатки наличных денег у населения и вклады
населения в банках.
Агрегированные показатели:
эффективность производства, технический
уровень предприятий, качество продукции,
экологическое состояние
4. Типы временных рядов
1. имеющие тенденцию, характеризующую долговременноесовокупное воздействие множества факторов на динамику
изучаемого показателя;
2. подверженные циклическим колебаниям, которые могут
носить сезонный характер;
3. фактический уровень временного ряда можно представить
как сумму (аддитивная модель) или произведение
(мультипликативной модель) трендовой, циклической и
случайной компонент.
5. Автокорреляция уровней временного ряда и выявление его структуры
Одна из рабочих формул для расчётакоэффициента автокорреляции имеет вид:
В качестве переменной х мы рассмотрим
ряд y2, y3, … , yn; в качестве переменной
у – ряд y1, y2, . . . ,yn – 1 . Тогда приведённая
выше формула примет вид:
Аналогично
можно
определить
коэффициенты автокорреляции второго и
более высоких порядков. Так, коэффициент
автокорреляции
второго
порядка
характеризует тесноту связи между уровнями
уt и yt – 1 и определяется по формуле :
где
где
6.
Число периодов, по которым рассчитываетсякоэффициент автокорреляции, называют лагом.
Свойства коэффициента автокорреляции
Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким
образом характеризует тесноту только линейной связи текущего и предыдущего уровней
ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной
(или близкой к линейной) тенденции.
Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о
возрастающей или убывающей тенденции в уровнях ряда. Большинство временных
рядов экономических данных содержит положительную автокорреляцию уровней,
однако при этом могут иметь убывающую тенденцию.
Последовательность
коэффициентов
автокорреляции
уровней
первого,
второго
и
т.
д.
порядков
называют
автокорреляционной
функцией временного ряда.
График зависимости её значений от
величины лага (порядка коэффициента
корреляции)
называется
коррелограммой.
7. Моделирование тенденции временного ряда
Для построения трендов чаще всего применяются следующие функции:· линейный тренд: yt
= a0 + a1t;
· тренд в форме степенной функции:
· гипербола: yt =a0 + a1/t;
yt = atb;
· экспоненциальный тренд: yt = e a + bt ; · парабола второго и более порядков:
yt = a0 + a1t + a2 t 2 + . . . +ak t k .
Общие соображения при выборе типа линии, по которой производится аналитическое выравнивание ,
могут быть сведены к следующим:
1) Если абсолютные приросты уровней ряда по своей величине колеблются около постоянной
величины, то математической функцией, уравнение которой можно принять за основу аналитического
выравнивания, следует считать прямую линию:
yt = a0 + a1 t, где yt считается как у, выровненный по t.
2) Если приросты приростов уровней, то есть ускорения, колеблются около постоянной величины, то
за основу аналитического выравнивания, следует принять параболу второго порядка:
yt = a 0 + a 1 t + a 2 t 2 .
Показатели а0, а1 и а2 представляют собой в каждом отдельном случае выравнивания постоянные
величины, называемые параметрами: а0 –начальный уровень; а1 – начальная скорость ряда и а2 –
ускорение или вторая скорость.
3) Если уровни изменяются с приблизительно постоянным относительным приростом, то
выравнивание производится по показательной (экспонентной функции):
yt = a0 a1t.
Величина отклонений и лежит в основе расчёта остаточной дисперсии:
8. Метод наименьших квадратов
Метод наименьших квадратовоснован на требовании о том, чтобы сумма квадратов отклонений фактических данных от
2
2
2
; выровненных была наименьшей: (у1 – у1) + (у2 – у2) + . . . + (уn – yn) = S
Принцип, положенный в основу метода наименьших квадратов, может быть записан в
сжатом математическом виде следующим образом:
.
;
∑ (y – yt)2 = min.
Имеем:
∑ (y – yt )2 = S;
Найдём минимум функции, используя уравнение параболы.
и получаем:
заменяем:
yt = a0 + a1 t + a2 t 2
∑( y - a0 - a1 t - a2 t 2 )2 = S.
Находим частные производные функции S сначала по параметру а0, а затем по а1 и а2, и
приравниваем их к нулю.
Преобразовывая, получаем:
При выравнивании по показательной функции yt = a0 a1t параметры а0 и а1 определяются по
методу наименьших квадратов отклонений логарифмов путём решения системы нормальных
уравнений:
9. Приведение уравнения тренда к линейному виду
Если тренд представлен степенной линией регрессии, то есть он имеетвид: yt = a0ta1, то логарифмируя обе части равенства, получим:
ln yt = ln a0 + a1 ln t.
Отсюда видно, что, введя новые переменные z=ln yt, x=ln t, мы
получим уравнение вида z=b0 +a1x, где b0=ln a0.
Это обычное линейное уравнение. Если линия тренда – парабола
второго порядка yt = a0 + a1 t + a2 t 2 , то заменой вида:
х1=t, x2=t 2, мы получим линейную функцию двух переменных:
yt=a0 + a1 х1 + a2 х2 .
Оценку параметров такой функции можно провести методами
линейного регрессионного анализа для множественной регрессии.
10. Оценка параметров уравнения регрессии
Оценка параметров уравнения регрессииЛинейный коэффициент корреляции ryt :
-1 ≤ ryt ≤ 1
или
Коэффициент детерминации:
где
- общая дисперсия результативного признака у
- остаточная дисперсия, определяемая, исходя из уравнения
регрессии уt = f(t)
Величина 1 – r 2 характеризует долю дисперсии у, вызванную влиянием
остальных, не учтённых в модели факторов.
Уравнение нелинейной регрессии, так же как и в линейной зависимости,
дополняется показателем корреляции, а именно индексом корреляции R:
Иначе, индекс корреляции
можно выразить как
Величина
данного
показателя
находится
в
границах:
0 ≤ R ≤ 1, чем ближе к единице, тем теснее связь рассматриваемых признаков,
тем
более
надёжно
найденное
уравнение
регрессии.
11.
Когда преобразования уравнения в линейнуюформу связаны с зависимой переменной, квадрат
значения коэффициента корреляции будет
характеризовать отношение факторной суммы
квадратов отклонений к общей, но не для у, а для
его логарифмов.
Индекс корреляции определяется по
формуле:
Индекс корреляции используется для проверки существенности в целом уравнения
нелинейной регрессии по F-критерию Фишера:
где
- индекс детерминации;
n – число наблюдений;
m – число параметров при переменных х.
Практически, если величина разности между индексом детерминации и
коэффициентом детерминации не превышает 0,1, то предположение о линейной форме
связи считается оправданным.
В противном случае проводится оценка существенности различия R2
вычисленных по одним и тем же исходным данным, через t – критерий Стьюдента:
m |R- r| - ошибка разности между R 2
и r2
, определяемая по формуле:
12. Аддитивная и мультипликативная модели временного ряда
Общий вид аддитивной модели:Y= T + S + E.
Общий вид мультипликативной модели:
Y = T∙S∙E.
Процесс построения модели включает в себя следующие шаги:
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты.
3.
Устранение сезонной компоненты из исходных уровней ряда и получение
выровненных данных в аддитивной или мультипликативной модели.
4.
Аналитическое выравнивание уровней и расчет значений тренда с использованием
полученного уравнения тренда.
5. Расчет полученных по модели значений или
6. Расчет абсолютных и относительных ошибок.
13. Стационарные временные ряды
Послеудаления
тенденции
(тренда)
получаем стационарный временной ряд.
из
временного
ряда
Последовательность случайных величин у1, у2, . . . или . . ., у-1, у0, у1, . . .
называется случайным процессом с дискретным параметром
времени.
Случайный процесс y(t) с непрерывным параметром времени можно
определить для 0 ≤ t < ∞ или -∞ < t < ∞ и рассматривать с привлечением
вероятностной меры на пространстве функций y(t).
Стационарность – упрощение модели
после расширения конечной
последовательности наблюдений до бесконечной
14. Применение быстрого преобразования Фурье к стационарному временному ряду
Пусть число данных N представимо в виде N = N1 N2. Тогда можно записатьt = t1 + (t 2-1)N1 , t1 = 1, . . ., N1 , t2 = 1, . . ., N2 ;
j = j1 + j 2N2 , j1 = 0, . . ., N2 – 1 , j2 = 0, . . ., N1 - 1;
Отметим, что aN – j = aj и bN – j = - bj .
Искомые коэффициенты являются соответственно действительной и мнимой частями суммы:
Для их отыскания вычислим сначала величины :
Для каждой пары ( j1, t1 ) , j1 = 0, . . ., N2 – 1 и t1 = 0, . . ., N1 . Поскольку
и
то существует около N1N2/2 = N/2 таких пар. После этого находятся действительная и
мнимая части суммы:
для j = 0,1, . . ., [N/2].
15. Автокорреляция остатков. Критерий Дарбина - Уотсона
Автокорреляция остатков.Критерий Дарбина - Уотсона
представляет собой «отношение фон Неймана»,
применённое к остаткам оценки.
Выражение
Значение d в выборке зависит одновременно от последовательности zt и от значений et ( для t
= 1,2, . . . ,N). Однако Дарбин и Уотсон показали, что для заданных значений et значение d
обязательно заключено между двумя границами d
U
и d
L
, не зависящими от значений,
принимаемых zt , и являющимися функциями лишь чисел N, именно d L £ d £ d U.
Интервал [d L,d U] является, следовательно, наименьшим из возможных, если не принимать
во внимание точные значения zt.
Границы d
U
и d
L
представляют случайные величины, распределение которых можно
определить с помощью точных гипотез относительно распределения et.
Для практического использования таблицы полученное значение d* следует сравнить
с d1 и d2.
а) Если d* < d1, то вероятность столь малого значения наверняка меньше a.
Гипотеза независимости отбрасывается.
б) Если d* > d2, то вероятность столь малого значения наверняка больше a.
Гипотеза независимости не отбрасывается.
в) Если d 1 £ d* £ d 2 , то приведённые таблицы оставляют вопрос открытым.














 Математика
Математика








