Похожие презентации:
Временные ряды
1. Временные ряды
2.
Временнойряд
(ВР)
–
это
данные,
характеризующие один и тот же объект в различные
моменты времени (временной срез)
y1 , y2 ,..., yn или yt (t 1, n) .
yt (t 1, n) – уровни (элементы) ряда, где п –
число уровней.
Каждый уровень ВР формируется под воздействием
факторов, которые условно подразделяются на
составляющие:
факторы, формирующие тенденцию (тренд) ряда;
факторы,
формирующие
периодические
колебания ряда;
случайные факторы.
3.
Тренд или тенденция Т ВР – это систематическая(неслучайная) составляющая, определяющее общее
направление развития ВР.
Наряду с тенденциями во ВР часто имеют место
более или менее регулярные колебания – периодические
составляющие.
Если период колебаний ≤1 года, то их называют
сезонными S.
При большем периоде колебания – имеет место
циклическая составляющая С.
Циклические
изменения
не
обязательно
периодические.
Если из ВР удалить тренд и периодические
составляющие, то останется нерегулярная (случайная)
компонента U.
4.
Модель, в которой ВР представлен в виде суммысоответствующих
компонент,
называется
аддитивной. Модель, в которой ВР представлен в
виде произведения – мультипликативной:
аддитивные модели ряда
yt T C S U ,
мультипликативные модели
yt T C S U .
Смешанные модели
yt T C S U
5.
Решение задачи по ВР начинается с построения графика.Динамика производства электроэнергии в РФ (млн. кВт.ч )
Тенденция этого ряда была близка к линейному развитию.
Видны устойчивые сезонные колебания, имеющие годовую
периодичность.
6.
Временной ряд объема импорта РФ.Заметен растущий тренд.
Ярко выражена сезонная составляющая с минимумом в
январе и максимумом в декабре.
7.
ИССЛЕДОВАНИЕ ТЕНДЕНЦИИВРЕМЕННОГО РЯДА
8.
Проверка гипотезы о существовании тренда.Для выявления факта наличия или отсутствия
неслучайной составляющей, т.е. для проверки
гипотезы о независимости средней ВР от времени:
H o : М ( y(t )) a const ,
используют следующие критерии.
9.
Метод сравнения средних.ВР разбивают на 2 примерно равные части n1 и n2:
Y2 ( y n 1 ,... y n ) ,
Y1 ( y1 ,... y n )
и
каждая
из
которых
самостоятельная выборочная совокупность, имеющие
нормальное распределение.
Решаются две задачи.
1
1
2
Если ВР имеет тенденцию, то Y1 и Y2 должны
существенно различаться между собой.
Проверяется гипотеза о равенстве средних:
H 0 : M (Y1 ) M (Y2 ) .
За основу проверки берется t-критерий Стьюдента.
10.
В случае равенства дисперсий ( 12 22 ):Y1 Y2
t набл
t ( , v n1 n2 2) , где
1 1 ~
SY Y
1 2
n1 n2
SY1 Y2 – выборочное среднеквадратическое отклонение:
SY1 Y2
(n1 1) 2 S12 (n2 1) 2 S 22
, где
n1 n2 2
n
n1
S
2
1
2
(
y
Y
)
i 1
i 1
n1 1
и
S 22
2
(
y
Y
)
i 2
i n1 1
n2 1
11.
Проверка гипотезы о равенстве дисперсий0 : 12 22 ; 1 : 12 22
осуществляется с помощью F-критерия:
Fрасч
где дисперсии для 1–ой
рассчитываются по формуле:
si2
Если
2
2
2
1
s
,
s
и
2–ой
частей
ряда
2
(
y
y
)
i i
n 1
Fрасч Fкрит , то гипотеза о равенстве
дисперсий принимается. Если Fрасч
о равенстве дисперсий отклоняется.
Fкрит , то гипотеза
12.
АВТОКОРРЕЛЯЦИЯУРОВНЕЙ ВРЕМЕННОГО РЯДА.
13.
При наличии во ВР тенденции и периодическихколебаний
значения
каждого
yt
зависят
от
y1, y2 ,..., yt 1 .
Корреляционная
зависимость
между
последовательными
уровнями
ВР
называется
автокорреляцией уровней.
Степень тесноты корреляционной связи между
yt
может
быть
определена
с
коэффициентов автокорреляции, т.е.
коэффициентом
корреляции
помощью
линейным
между
y1 , y2 ,..., yt ,..., yn и y1 , y2 ,..., yt ,..., yn .
14.
Формула для расчета коэффициента корреляцииимеет вид:
r ( )
M [( yt a yt )( yt a yt )]
D( yt ) D( yt )
cov( yt , yt )
( yt ) ( yt ) .
Число периодов, по которым рассчитывается
коэффициент автокорреляции, называют лагом.
Выборочной оценкой r ( ) является выборочный
коэффициент автокорреляции r :
cov( yt , yt )
r
( yt ) ( yt )
15.
Свойства коэффициента автокорреляции.r характеризует тесноту только линейной связи
1.
текущего и предыдущего уровней ряда.
2. Для ВР, имеющего сильную нелинейную
тенденцию, r может приближаться к нулю.
3. По знаку r нельзя делать вывод о возрастающей
или убывающей тенденции в уровнях ряда. Большинство
ВР экономических данных содержат положительную
автокорреляцию уровней, однако при этом могут иметь
убывающую тенденцию.
16.
Порядоккоэффициентов
автокорреляции
определяется временным лагом.
Последовательность
коэффициентов
автокорреляции
r(1),
r(2)
и
т.д.
называют
автокорреляционной функцией ВР (АКФ).
График зависимости ее значений от величины лага
называется коррелограммой.
17.
При помощи АКФ можно выявить структуру ВР:если наиболее высоким оказался r(1), то исследуемый
ряд содержит только линейную тенденцию.
если наиболее высоким оказался r( ), то ряд содержит
циклические колебания с периодичностью в
моментов времени.
если ни один из коэффициентов автокорреляции не
является значимым, то либо ряд не содержит тенденции
и циклических колебаний, либо ряд содержит сильную
нелинейную тенденцию.
18.
ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВС ПОМОЩЬЮ КРИВЫХ РОСТА
19.
Одним из приемов изучения общей тенденции во ВРявляется аналитическое выравнивание.
Аналитическим выравниванием ВР называют
нахождение аналитической функции времени ŷ=f (t),
характеризующей основную тенденцию изменения
уровней ряда с течением времени.
Функция f(t) носит название кривой роста.
20.
Основные виды кривыхКривая роста позволяет получить выровненные или
теоретические значения уровней ВР - yˆt (это уровни,
которые наблюдались бы в случае полного совпадения
динамики явления с кривой).
Процедура разработки прогноза с использованием
кривых роста включает в себя следующие этапы:
1) выбор одной или нескольких кривых, форма
которых соответствует характеру изменения ВР;
2) оценка параметров выбранных кривых;
3) проверка адекватности выбранных кривых и
окончательный выбор кривой роста;
4) расчет точечного и интервального прогнозов.
21.
Наиболее часто на практике используются кривые ростатрех основных типов.
I класс – функции, используемые для описания процессов
с монотонным характером развития без предела роста.
2
p
полиномы yˆ t a0 a1t a2t ... a p t ;
показательная - yˆ t ab t , где b – темп изменения;
линейно–логарифмическая – yˆ t a0 a1 ln t и др.
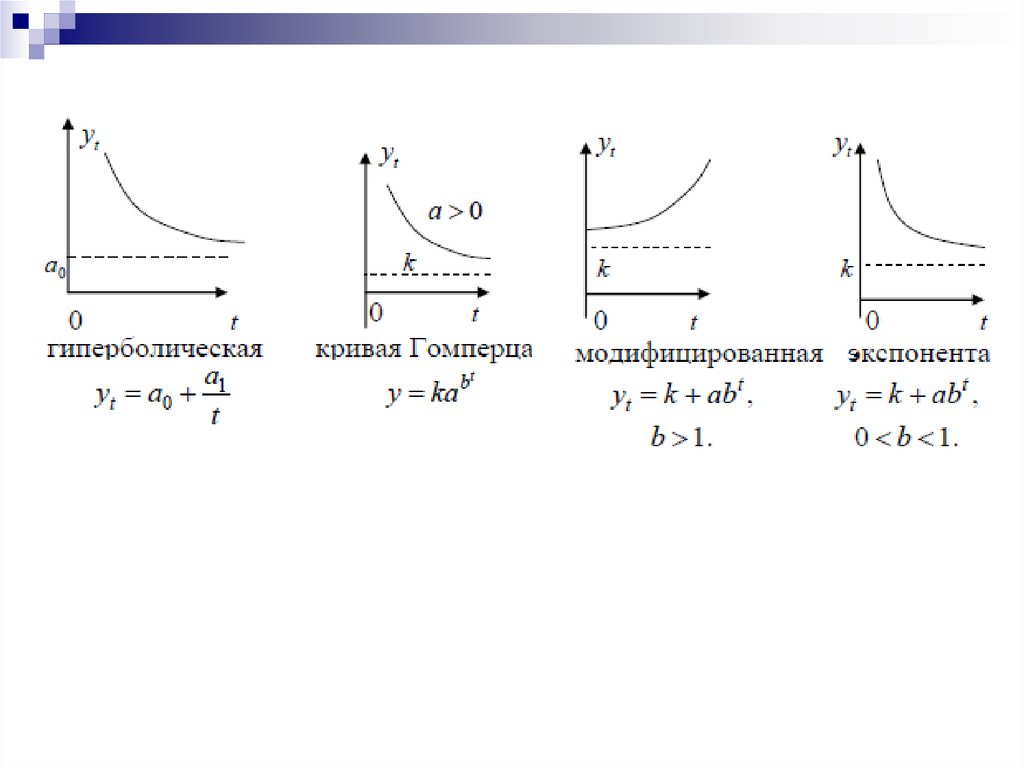
22.
II класс – кривые, описывающие процесс, который имеетпредел роста без точки перегиба. Такие кривые называются
кривыми с насыщением.
кривая Джонсона – yˆ t e
a0
a1
t
,
t
ˆ
y
k
a
a
модифицированная экспонента – t
0 1;
b
ˆ
y
a
гиперболической – t
;
t
кривая Гомперца – yˆt ka0
a1t
вторая функция Торнквиста – yˆ t a0
t
и др.
t a1
23.
24.
III класс – кривые, имеющие предел роста и точкиперегиба.
Такие кривые называются S-образными.
Описывают два последовательных лавинообразных
процесса (когда прирост зависит от уже достигнутого
уровня): один с ускорением развития, другой – с
замедлением.
25.
Определение параметров кривых ростаПараметры кривых роста, как правило, оцениваются по МНК,
например,
yt a0 a1t a2t 2 ... a p t p .
Оценки
выражения:
параметров находятся в результате минимизации
n
Q ( yt yˆ t ) 2 min
t 1
Система нормальных уравнений:
yt a0 n a1 t a2 t 2 ... a p t p
yt t a0 t a1 t 2 ... a p t p 1
......................................................................
p 1
p 1
p
2 p 1
y
t
a
t
a
t
...
a
t
t
0
1
p
p
p
p 1
2p
y
t
a
t
a
t
...
a
t
t
0
1
p
26.
Параметры прямой yt a0 a1t .Функция минимизируется, если взять частные производные по
неизвестным коэффициентам
n
Q
2 ( yi a0 a1 t i ) ( 1) 0
a0
i 1
.
n
Q
a 2 ( yi a0 a1 t i ) ( ti ) 0
1
i 1
yt a0 n a1 t
Система нормальных уравнений:
yt t a0 t a1 t 2
Решение этой системы:
yt
yt t n t
yt a t
a1
a
0
1
2
n
n
t
2
t n
27.
2Параметры квадратичного тренда yt a0 a1t a 2 t :
yt a0 n a1 t a2 t 2
2
3
y
t
a
t
a
t
a
t
t
0
1
2
2
2
3
4
y
t
a
t
a
t
a
t
t
0
1
2
Эта система содержит три уравнения, позволяющих найти оценки
трех неизвестных коэффициентов a0, a1, a2.
Величины t , t ... не зависят от конкретных уровней
динамического ряда, они являются функциями только числа членов в
ВР:
n(n 1)
n(n 1)( 2n 1)
2
t 2
t
6
n 2 (n 1) 2
n(n 1)( 2n 1)(3n 2 3n 1)
3
4
t 4
t
30
2
28.
Другой подход к упрощению расчетов – перенос началакоординат в середину ВР.
для четного числа членов ряда: t=…,–5;–3;–1;1;3;5; …;
для нечетного числа членов ряда: t=…,–3;–2;–1;0;1;2;3; …
Таким образом, tk=0 при k – нечетном числе.
В этом случае оценки параметров:
Прямой
yt t
yt
a1
a0
2
n
t
Параболы
yt t 2 n yt t 2 t 2 yt
a0
2
n
n n t4 t2
yt t
n yt t 2 t 2 yt
a1
a2
2
4
2 2
t
n t t
29.
Для полиномов предпочтительнее определять неизвестныекоэффициенты, используя матричные обозначения.
Для параболической функции yˆ a0 a1t a2t 2 .
В матричном обозначении неизвестные коэффициенты:
a (T T T ) 1T T Y ,
где
y
1
y2
Y
y
n
1 t
1
1 t
2
T
1 t
n
– вектор наблюдаемых значений временного ряда;
t12
t 22
2
tn
– матрица, характеризующая временные данные
(независимые переменные).
30.
ПРОВЕРКА АДЕКВАТНОСТИ И ТОЧНОСТИВЫБРАННЫХ МОДЕЛЕЙ
31.
Проверка адекватности выбранных моделей реальномупроцессу (в частности, адекватности полученной кривой
роста) строится на анализе случайной компоненты
et yt yˆ t .
Модель адекватна реальному явлению, если
выполняются наиболее важные свойства остаточной
компоненты et :
равенство математического ожидания нулю: Met 0 ;
случайность остатков;
независимость
последовательных
уровней
ряда
остатков;
соответствие
остатков
нормальному
закону
распределения.
32.
Проверка равенства математического ожидания нулюуровней ряда остатков
H 0 : M (et ) 0 .
Для этого строится t –статистика:
1
t расч
|e |
n
S
n
n
e
t 1
t
1 n
2
(
e
e
)
t
n 1 t 1
При уровне значимости α гипотеза
отклоняется, если t расч tкр ( , v n 1)
H 0 : M (et ) 0
Здесь t кр ( , v n 1) − критерий Стьюдента с уровнем
значимости α и (n −1) степенями свободы.
33.
Проверка случайности остатковДля проверки случайности отклонений уровней ряда от тренда
могут быть также использованы критерии:
▪ критерий «восходящих» и «нисходящих» серий;
▪ критерий пиков, или критерий поворотных точек.
Опишем второй критерий.
Значение случайной переменной считается поворотной точкой,
если оно одновременно больше (меньше) соседних с ним элементов:
et 1 et et 1 или et 1 et et 1 .
Критерий случайности отклонения от тренда при уровне
доверительной вероятности 0,95 можно представить как
pфакт p расч , где
p расч 2n 1 / 3 1,96 16n 29 90
– расчетное
поворотных точек;
p факт – фактическое количество поворотных точек.
количество
34.
Проверка независимости остатковНаиболее распространенным методом проверки наличия
автокорреляции первого порядка, т.е. автокорреляции между
соседними остаточными членами ряда, является критерий Дарбина–
Уотсона.
Значение этого критерия определяется по формуле:
n
d
2
e
e
t t 1
t 2
n
e
t 1
2
t
35.
Проверка нормальности распределения остатковПри нормальном распределении показатели асимметрии (А) и
эксцесса (Е) равны нулю.
A
1 n 3
et
n t 1
1 n 2
et
n t 1
3
6 n 2
A
n 1 n 3
E
1 n 4
et
n t 1
1
2
et
n t 1
n
2
3
24n n 2 n 3
E
n 1 2 n 3 n 5
А – выборочная характеристика асимметрии;
Е – выборочная характеристика эксцесса;
A – среднеквадратическая ошибка выборочной характеристики
асимметрии;
E – среднеквадратическая ошибка выборочной характеристики
эксцесса.
36.
Если одновременно выполняются следующие неравенства:A 1,5 A ;
,
6
E n 1 1,5 E
то гипотеза о нормальном распределении случайной компоненты не
отвергается.
Если выполняется хотя бы одно из неравенств
6
A 2 A ; E
2 E ,
n 1
то гипотеза о нормальном характере распределения отвергается.
В случае попадания коэффициентов асимметрии и эксцесса в
зону неопределенности между 1,5 и 2 единиц среднеквадратического
отклонения
1,5 A A 2 A ;
6
1,5 E E
2 E
n 1
используются другие критерии, в частности RS–критерий.
37.
RS – критерий – один из самых простых критериев проверкинормальности закона распределения случайной величины, он
характеризует отношение размаха вариаций к стандартному
R
отклонению . Статистика RS рассчитывается по выборке:
S
emax emin
RS набл
, где
S
et yt yˆ t
–
остатки,
emax max (et ) ,
t
emin min (et ) ;
t
n
S2
2
(
e
e
)
t
t 1
n 1
.
Если a RS набл b (а – нижняя и b –верхняя границы), то
гипотеза о нормальном распределении ряда остатков принимается.
Если все пункты проверки дают положительные результаты, то
выбранная трендовая модель адекватна реальному ряду и ее можно
использовать для построения прогнозных оценок.
38.
Построение точечных и интервальных прогнозовДоверительный интервал определяется в виде:
yˆ n t , S np , где
n – длина временного ряда;
– период упреждения;
yˆ n – точечный прогноз на момент n+τ;
t , – значение критерия Стьюдента ( – уровень значимости и v n k 1
–степень свободы, k – количество параметров при независимых
переменных);
Sпp – средняя квадратическая ошибка прогноза.
39.
Стандартная ошибка прогноза зависит не только от числанаблюдений n, но и от периода упреждения и может быть
определена в матричной форме
S np S 1 T T (T T T ) 1 T ,
где S – стандартная ошибка уравнения; T – вектор-столбец времени,
по которому производится экстраполяция:
1
yˆt a0 a1t :
T
n
yˆ t a0 a1t a2t 2 :
S
1
T n
(n ) 2
Q
n k 1
n
2
и Q ( yi yˆ i ) , где
i 1
k – количество параметров при независимых переменных.






































 Математика
Математика








