Похожие презентации:
Производные. Механический, физический, геометрический и экономический смысл производных
1. Производные
ПРОИЗВОДНЫЕМеханический, физический, геометрический
и экономический смысл производных.
2. определение
Произво́дная (функции в точке) — основное понятиедифференциального исчисления, характеризующее
скорость изменения функции (в данной точке). Определяется
как предел отношения приращения функции к приращению
её аргумента при стремлении приращения аргумента к
нулю, если такой предел существует.
ОПРЕДЕЛЕНИЕ
3. Пример решения
ПРИМЕР РЕШЕНИЯ4. геометрический смысл
Производной функции y = f(x) в точке Х называется предел,если он существует, отношения приращения функции к
приращению аргумента при стремлении последнего к нулю.
2. геометрически – как угловой коэффициент касательной к
графику функции в этой точке.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
5. Пример решения
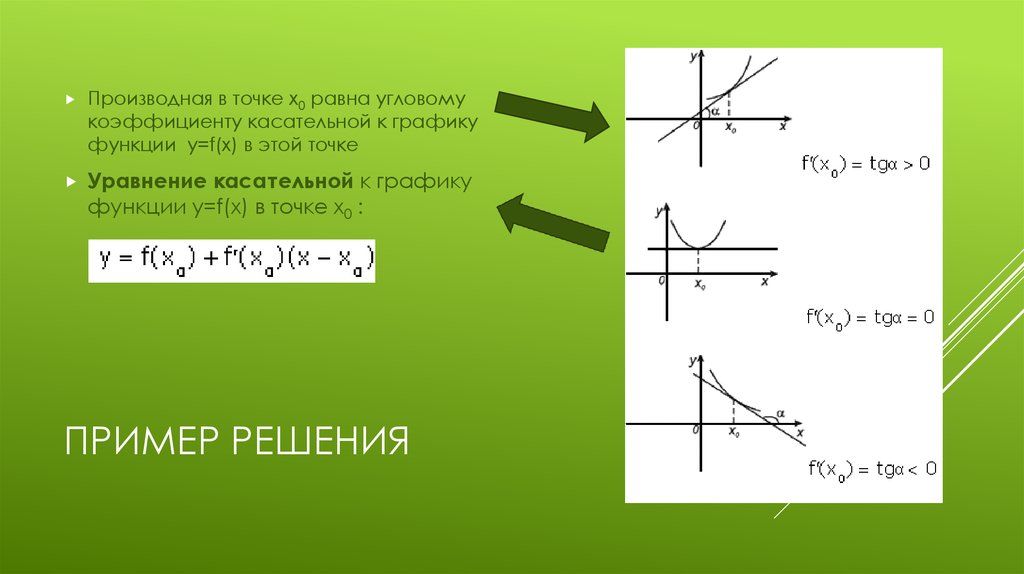
Производная в точке x0 равна угловомукоэффициенту касательной к графику
функции y=f(x) в этой точке
Уравнение касательной к графику
функции y=f(x) в точке x0 :
ПРИМЕР РЕШЕНИЯ
6. Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяетсяпо закону x(t), то мгновенная скорость точки:
ФИЗИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ.
7. Экономический смысл производной
Производительность труда есть производная объема продукции по времени.
ЭКОНОМИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ
8. Пример решения
ПРИМЕР РЕШЕНИЯ9. Механический смысл производной
МЕХАНИЧЕСКИЙ СМЫСЛПРОИЗВОДНОЙ








 Математика
Математика








