Похожие презентации:
Определение производной, ее геометрический и физический смысл
1.
11.08.20201
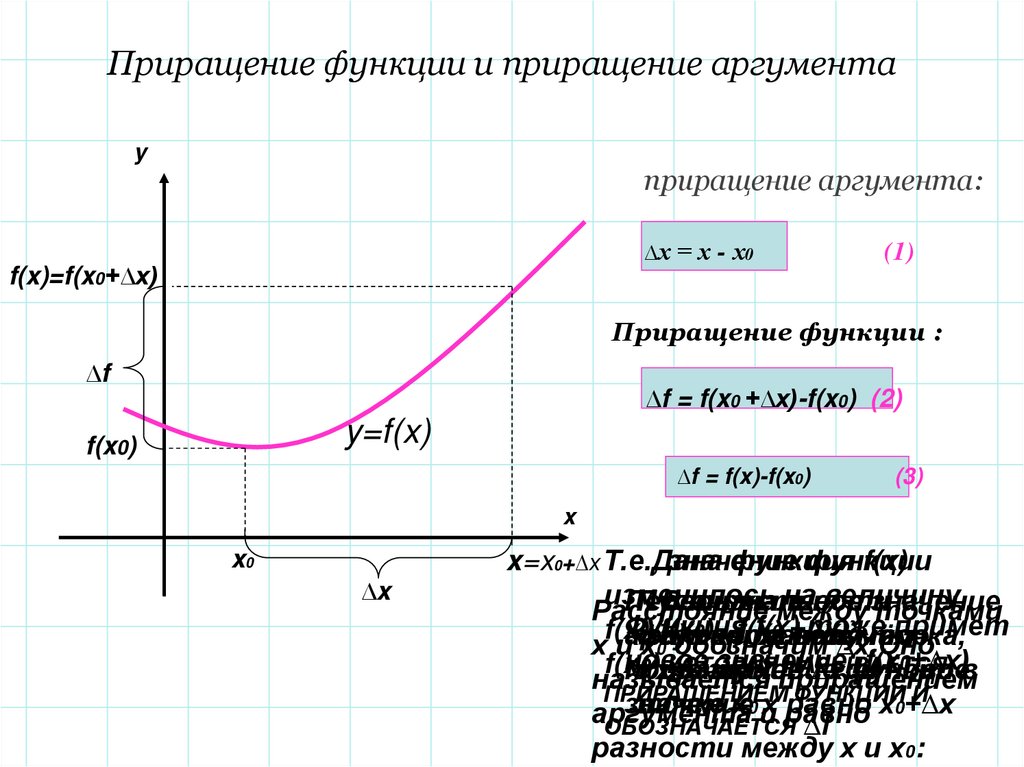
2. Приращение функции и приращение аргумента
yприращение аргумента:
∆х = х - х0
f(x)=f(x0+∆x)
(1)
Приращение функции :
∆f
∆f = f(x0 +∆x)-f(x0) (2)
y=f(x)
f(x0)
∆f = f(x)-f(x0)
(3)
x
x0
∆x
x=x0+∆x Т.е.,Дана
значение
функция
функции
f(x)
изменилось
на величину
Первоначальное
Пусть
В окрестности
х0- между
значение
Расстояние
точками
Функция
f(х)
тоже
примет
f(x)-f(x
0)= f(x
фиксированная
х00 +∆x)возьмём
получило
точка,
х иаргумента
х0точки
обозначим
∆х.Оно
новое
значение:
0+∆x)в
f(x
0),точку
КОТОРАЯ
НАЗЫВАЕТСЯ
приращение
f(х
0)- значение
х приращением
∆х,функци
иf(xновое
называется
ПРИРАЩЕНИЕМ ФУНКЦИИ И
значение
точке х0 и
х равно
равно х0+∆х
аргумента
ОБОЗНАЧАЕТСЯ ∆f
разности между х и х0:
3. Задача 1 (о скорости движения). Стр.157
• По прямой, на которой заданы началоотсчета, единица измерения и
направление, движется некоторое тело.
• Закон движения задан формулой s=s (t), где
t — время, s (t) — положение тела на прямой
(координата движущейся материальной
точки) в момент времени t по отношению к
началу отсчета.
• Найти скорость движения тела в момент
времени t.
4.
Предположим, что в момент времени t тело находилось в точке Мпройдя путь от начала движения ОМ = s{t). Дадим аргументу t
приращение ∆t и рассмотрим момент времени t+∆t Координата
материальной точки стала другой, тело в этот момент будет
находиться в точке P : OP=s(t+∆t) Значит, за ∆t секунд тело переместилось из точки
М в точку Р, т.е. прошло путь МР. Имеем:
MP=OP-OM=s(t+∆t)-s(t)=∆s
Полученную разность мы назвали приращением функции
Путь ∆s тело прошло за ∆t секунд.
v
Нетрудно найти среднюю скорость ср движения тела за промежуток времени
[t;t+∆t] :
vср
=
s
t
А что такое скорость v (t) в момент времени t (ее называют иногда
мгновенной скоростью)? Можно сказать так: это средняя скорость движения
за промежуток времени [t;t+∆t] при условии , что ∆t выбирается все меньше и
меньше; точнее: иными словами, при условии, что ∆t→0.Это значит , что
Подводя итог решению задачи 1, получаем:
v t lim vср
t 0
v(t ) lim
s
t
t 0
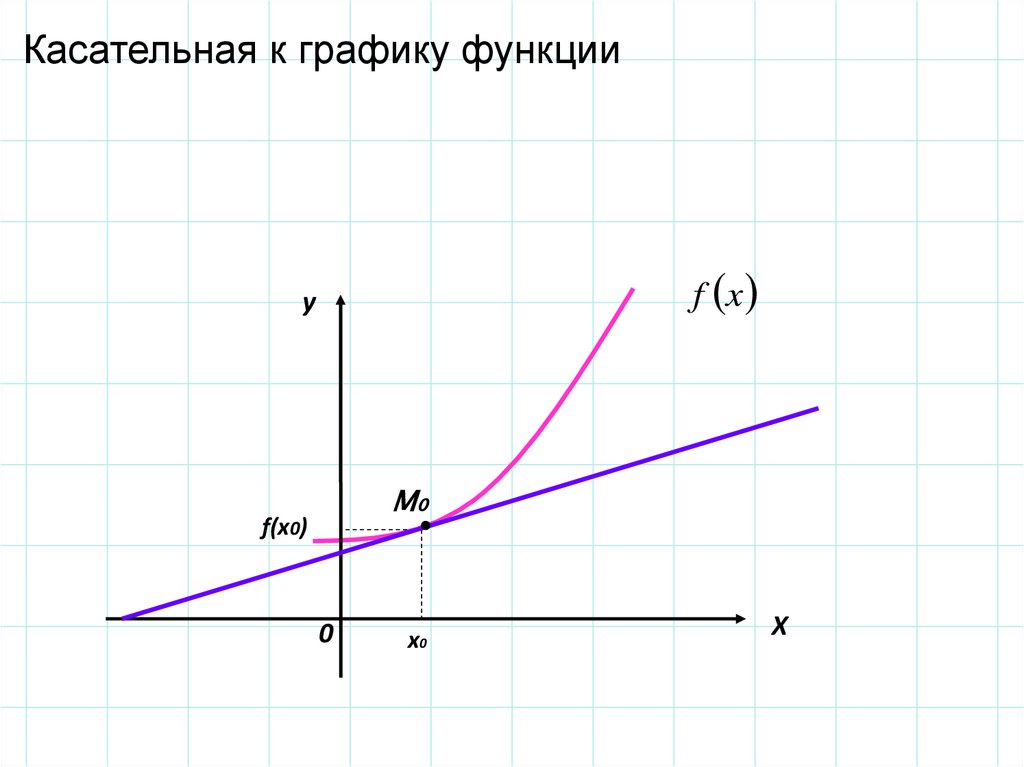
5.
Касательная к графику функцииf x
y
M0
f(x0)
0
x0
X
6.
ЗАДАЧА 2 (О КАСАТЕЛЬНОЙ КГРАФИКУ ФУНКЦИИ СТР.158
y
А
В
М(х ,у)
∆f(x) = f(x) - f(x0)
М0(х0 ,у0)
С
∆х=х-х0
α
β
x0
y = f(x)
x
x
7. Определение производной стр.159-160
Производной функции f в точке х0называется предел отношения приращения
функции к приращению аргумента при
последнем стремящимся к нулю:
f ( x0 x) f ( x0 )
f x lim
x O
x
8.
Алгоритм нахожденияпроизводной
1. Зафиксировать значение х, найти f(x).
2. Дать аргументу х приращение ∆х, перейти в новую
точку х + ∆х, найти f(x + ∆х).
3. Найти приращение функции: ∆f = f(x + ∆х) – f(x).
4. Составить отношение
5. Вычислить
lim
∆x→0
∆f
.
∆х
∆f .
∆х
6. Этот предел и есть f ′(x).
9. А л г о р и т м
Алгоритм1)
2)
3)
4)
∆x = x – x0
∆f = f(x+x0) – f(x0)
f ( x0 x) f ( x0 )
f
x
x x0
f
f ( x0 ) lim
x 0 x
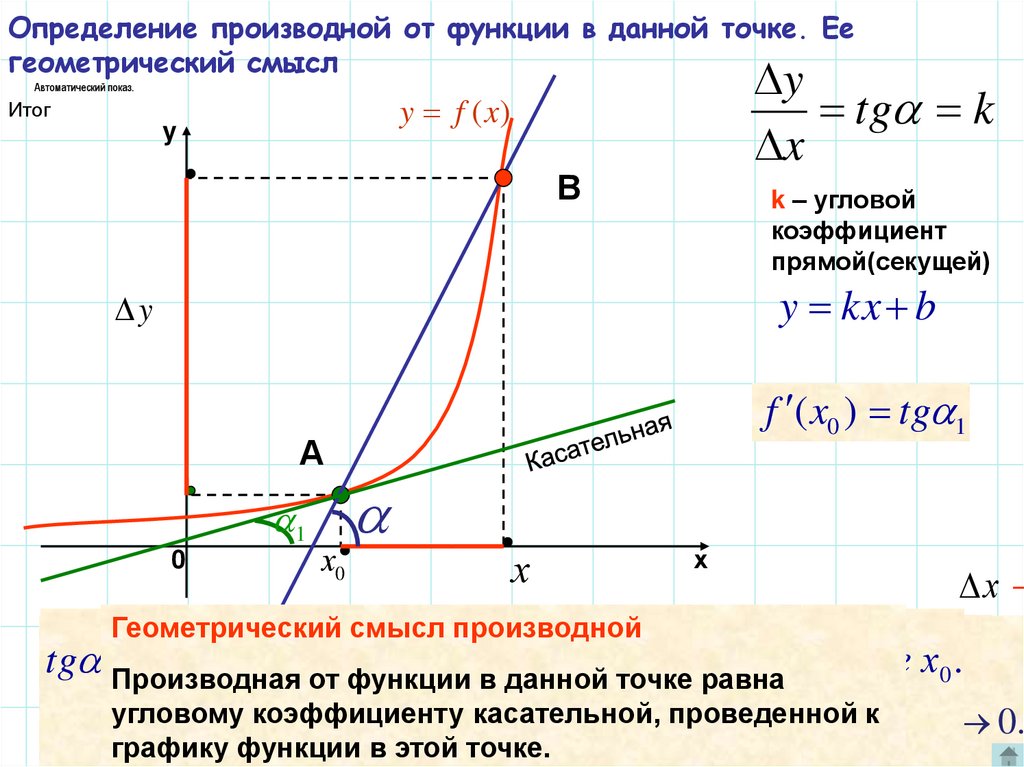
10. Определение производной от функции в данной точке. Ее геометрический смысл
Автоматический показ.y
tg k
x
y f (x)
Итог
y
В
k – угловой
коэффициент
прямой(секущей)
y kx b
y
f ( x0 ) tg 1
А
1
0
х0
х
х
х
Геометрический
смысл
производной
При
х
угловой
коэффициен
тх0секущей
к угловому
йy0функции
Производно
f
(
x
)
в
точке
называется
tg Производная
k
от
f (функции
x0 ) (производно
йточке
от равна
f ( x) в точке х0 .
в
данной
коэффициен
x ту касательной.
f ( x) к
угловому
коэффициенту
касательной,
проведенной
число, к которому стремится отношение
при х 0.
прив этой
х точке.
0
графику функции
x
11.
Физический смысл производной функциив данной точке
х
Vср.
t
Или, если х перемещение тела, а t промежуток времени ,
в течении которого выполнялось движение, то
х
средняя скорость движения на промежутке времени t.
t
При t 0 Vcр. к мгновенной скорости V (t ),
следовательно, V (t ) S (t ).
S (t ) V (t )
или х (t ) V (t )
Производная от функции в данной точке это
скорость изменения функции .
f ( х) V ( x)
.
12. Основные формулы
• Средняя скоростьvср
s
= t
• Мгновенная скорость s
v(t ) lim
v
t
lim
v
ср
или
t
t 0
t 0
• Скорость изменения функции
f x0 x f x0
lim
x 0
x
• Значение производной в точке
f ( x0 x) f ( x0 )
f x lim
x O
x
=
k tg
13.
Пример вычисления производнойКонспект
Дано : f ( x) x 2 1.
Найдем f ( x) в точке х0 2, то есть f ( 2).
Решение
f ( x) f ( x0 x) f ( x0 )
f ( x0 x) f ( 2 x) ( 2 x) 2 1
4 4 x x 2 1 5 4 x x 2
f ( x0 ) ( 2) 2 1 4 1 5
f ( x) 5 4 x x 2 5 4 x x 2
f ( x) 4 x x 2
4 x
x
x
f ( x)
Если x 0, то
4, то есть f ( x) 4.
x
Ответ : f ( x) 4.
14. Решить в классе
• 27.1(а,б)-27.5(а,б).11.08.2020
14
15. Домашнее задание.
§27, 27.1(в)-27.5(в).11.08.2020
15






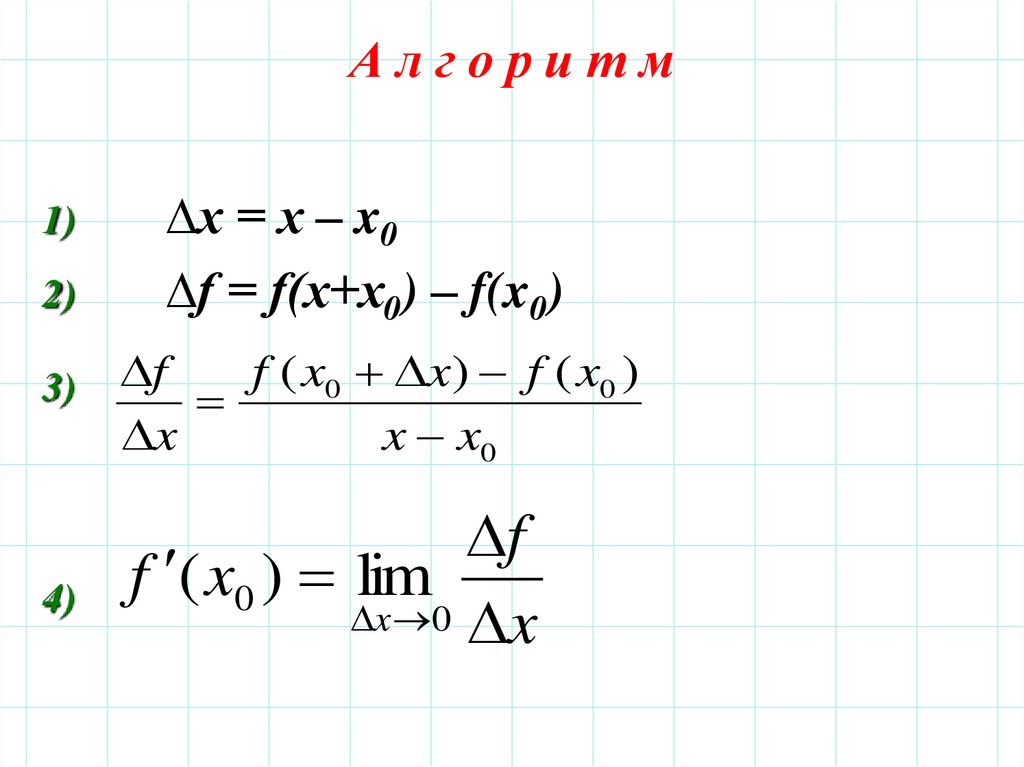






 Математика
Математика








