Похожие презентации:
Неравновесные явления в растворах электролитов
1.
Неравновесные явления в растворах электролитов1
2.
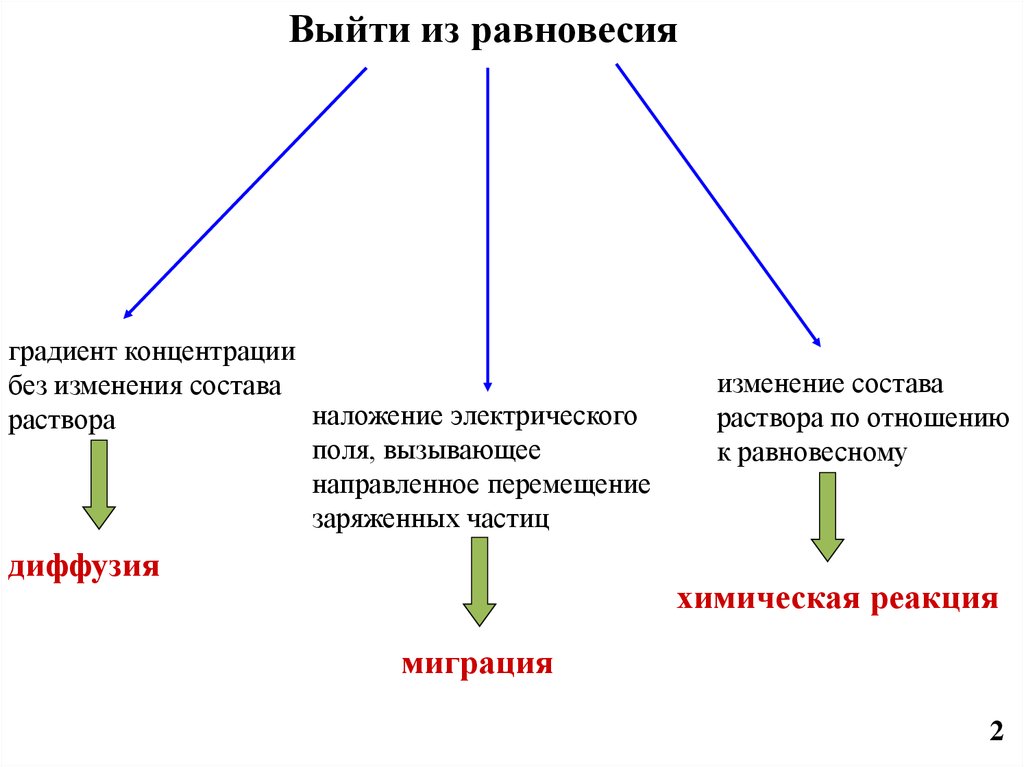
Выйти из равновесияградиент концентрации
без изменения состава
наложение электрического
раствора
поля, вызывающее
направленное перемещение
заряженных частиц
диффузия
изменение состава
раствора по отношению
к равновесному
химическая реакция
миграция
2
3.
Диффузияградиент концентрации
Движение ионов в растворе происходит по принципу прыжка с одного места в
растворителе в другое.
длина прыжка
1l
jпр
c
2
l
поток частиц в
прямом
направлении
j jпр jобр
G
G
1
l
RT
RT
jпр 1 e
c 1 e
2
время между прыжками
учёт вероятности
прыгнуть в
каждую сторону
S
Если параметры раствора (температура, давление, концентрация частиц)
меняются незначительно на длине прыжка, то можно считать изменение энергии
Гиббса малым. С этой оговоркой разложением в ряд можно пользоваться всегда.
j
1l
2
c 1 e
G
RT
1 l G
c
2
RT
d
G x l x l
dx
l2 1 d
j c
2 RT dx
3
4.
Диффузия0 RT ln a 0 RT ln c
f (c)
d
d (ln ln c)
d ln c d ln
1 dc d ln
d ln d ln c d ln c
RT
RT
RT
1
RT
1
dx
dx
d
ln
c
dx
dx
dx
d
ln
c
c
dx
d
ln
c
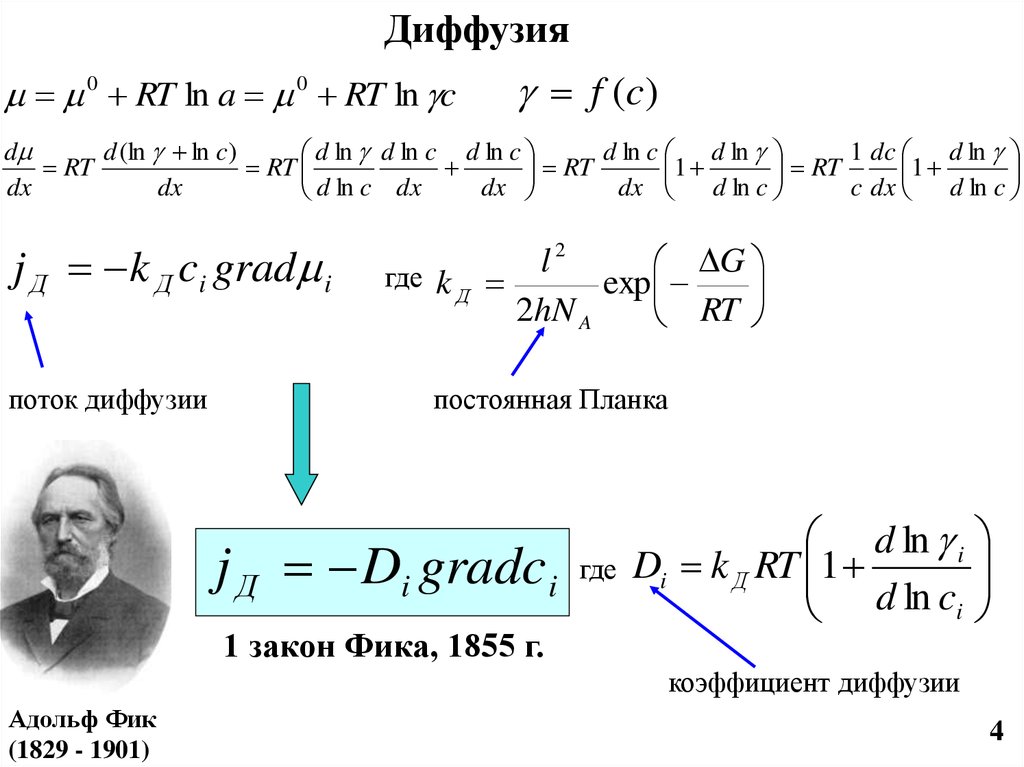
j Д k Д ci grad i
поток диффузии
2
l
G
где k
exp
Д
2hN A
RT
постоянная Планка
j Д Di gradc i
1 закон Фика, 1855 г.
где
d ln i
Di k Д RT 1
d ln ci
коэффициент диффузии
Адольф Фик
(1829 - 1901)
4
5.
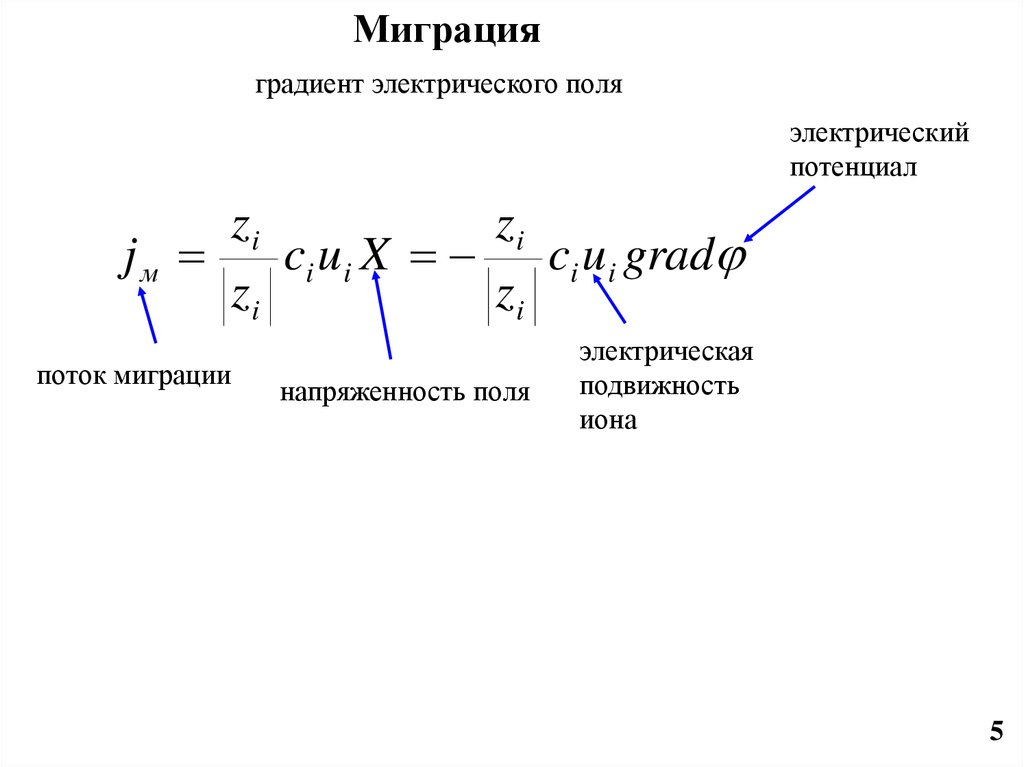
Миграцияградиент электрического поля
электрический
потенциал
zi
zi
jм
ci u i X
ci u i grad
zi
zi
поток миграции
напряженность поля
электрическая
подвижность
иона
5
6.
Диффузия и миграцияj = jД + jМ
Из химической термодинамики: G
i
N
i Nj i ,T , p
d G SdT VdP i dN i F zi dN i
i
i
электрохимический потенциал
Если ионы сорта i, в среднем,
не перемещаются в растворе
i i zi F
Эдвард
Гуггенгейм
(1901-1970)
grad i grad zi Fgrad 0
jД + jМ = 0
zi
k Д ci grad i ui ci grad
zi
d ln i
Di k Д RT 1
d ln ci
G
i
N i Nj i ,T , p
ui
kД
zi F
RT d ln i
1
Di ui
zi F d ln ci
6
7.
Уравнение Нернста-ЭйнштейнаДля идеального раствора ci → 0, γi → 1, Di=Di0, ui=ui0
RT 0 kT 0
Di
ui
ui
zi F
zi e0
0
Альберт Эйнштейн
(1879-1955) 1921 г. –
Нобелевская
премия по физике.
Уравнение Нернста-Эйнштейна
Вальтер Герман Нернст
(1864-1941) 1920 г. –
Нобелевская
премия по химии.
7
8.
ЭлектропроводностьI
+
-
R
U IR
R Ом
I
ρ – удельное сопротивление;
l – длина проводника (расстояние между
r Ом м электродами);
s – площадь поперечного сечения
проводника (площадь электродов).
R r
r
+
S
l
вещество
l
S
1
См/м
серебро
62 500 000
медь
58 100 000
золото
алюминий
l
- удельная электропроводность
r S R
1 См
45 500 000
Ом
м
м
37 000 000
нихром
893 000
графит
125 000
вода морская
3
вода дистилл.
10−4
кварцевое стекло
Закон Ома: сила тока, текущего по однородному
металлическому проводнику, пропорциональна
падению напряжения на проводнике (И.В.
Савельев, «Курс общей физики», т. 2)
10−16
Сименс
м
электропроводность раствора
заключенного между двумя
параллельными электродами,
имеющими площадь по 1м2 и
расположенными на
расстоянии 1 м друг от друга.
8
9.
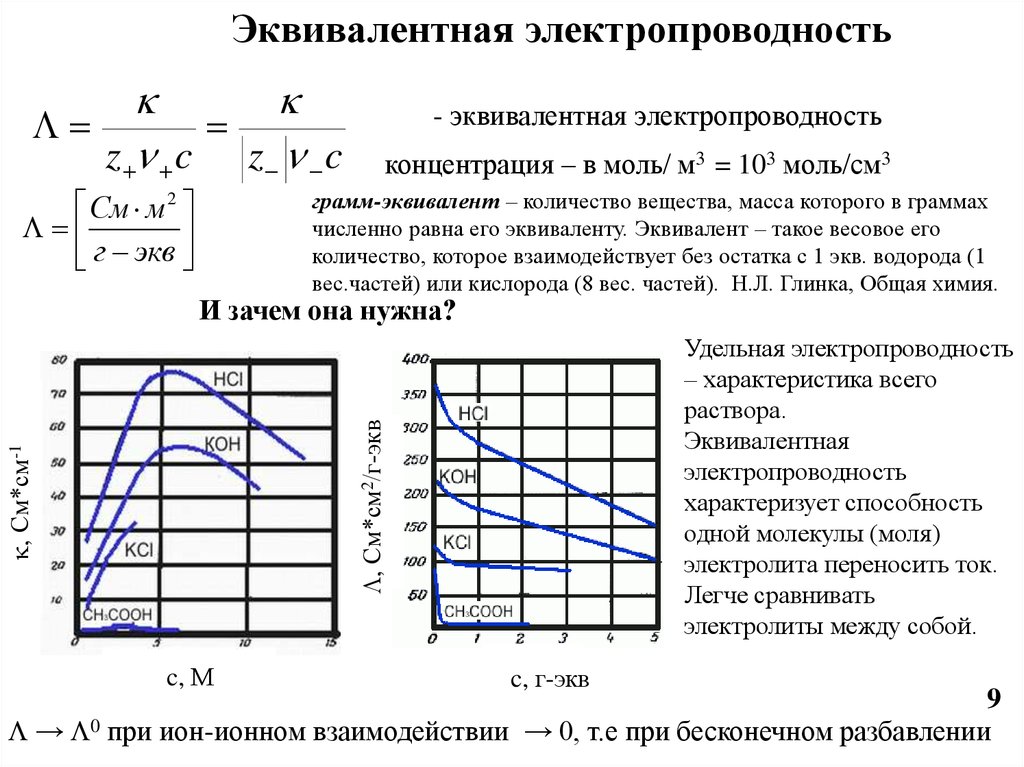
Эквивалентная электропроводностьz c z c
См м2
г
экв
- эквивалентная электропроводность
концентрация – в моль/ м3 = 103 моль/см3
грамм-эквивалент – количество вещества, масса которого в граммах
численно равна его эквиваленту. Эквивалент – такое весовое его
количество, которое взаимодействует без остатка с 1 экв. водорода (1
вес.частей) или кислорода (8 вес. частей). Н.Л. Глинка, Общая химия.
И зачем она нужна?
, См*см-1
, См*см2/г-экв
Удельная электропроводность
– характеристика всего
раствора.
Эквивалентная
электропроводность
характеризует способность
одной молекулы (моля)
электролита переносить ток.
Легче сравнивать
электролиты между собой.
c, М
c, г-экв
9
→ 0 при ион-ионном взаимодействии → 0, т.е при бесконечном разбавлении
10.
Молярная электропроводность разбавленных водныхрастворов электролитов при 25 С
С 0 1 а С bC
0
a
b
HCl
426
0.37
0.38
HClO4
417
0.36
0.4
HNO3
420
0.37
0.36
KOH
271
0.45
0.4
CsOH
271
0.45
0.5
AgNO3
133.3
0.68
0.35
KCl
149.8
0.63
0.64
NaCl
126.5
0.70
0.74
NaClO4
110
0.77
0.6
½BaCl2
139.5
1.28
1.74
169
2.48
3.6
Электролит
1/4K4Fe(CN)6
Для диапазона С = 0,001 – 0,1 М
11.
Электропроводностьнужны двое
Фридрих
Вильгельм
Кольрауш
(1840-1910)
,
0
- степень диссоциации
- ионные электропроводности или
подвижности ионов
= 1, сильные электролиты
λ+0, λ-0 - предельные
0
0
электропроводности (предельные
подвижности) ионов
Закон Кольрауша: катионы и анионы переносят
электрический ток независимо друг от друга
В переносе тока участвуют и катион, и анион, каждый движется к своему электроду.
Fu
Эмпирические
соотношения:
Fu
Слабые электролиты:
1
lg const lg c
2
Сильные электролиты:
0 const c
10
12.
Числа переносаЧисло переноса ti указывает, каков вклад ионов данного вида i в суммарную
удельную электропроводность.
Электрическое число переноса - доля тока, создаваемого ионами
данного вида i.
i
u
t
i u u
i
u
t
i u u
В растворе бинарного электролита t+ + t- = 1
ti
zi ci i
z
k
ck k
zi ci i
- если в растворе несколько электролитов
k
0i t i0 0
- предельная электропроводность иона
11
13.
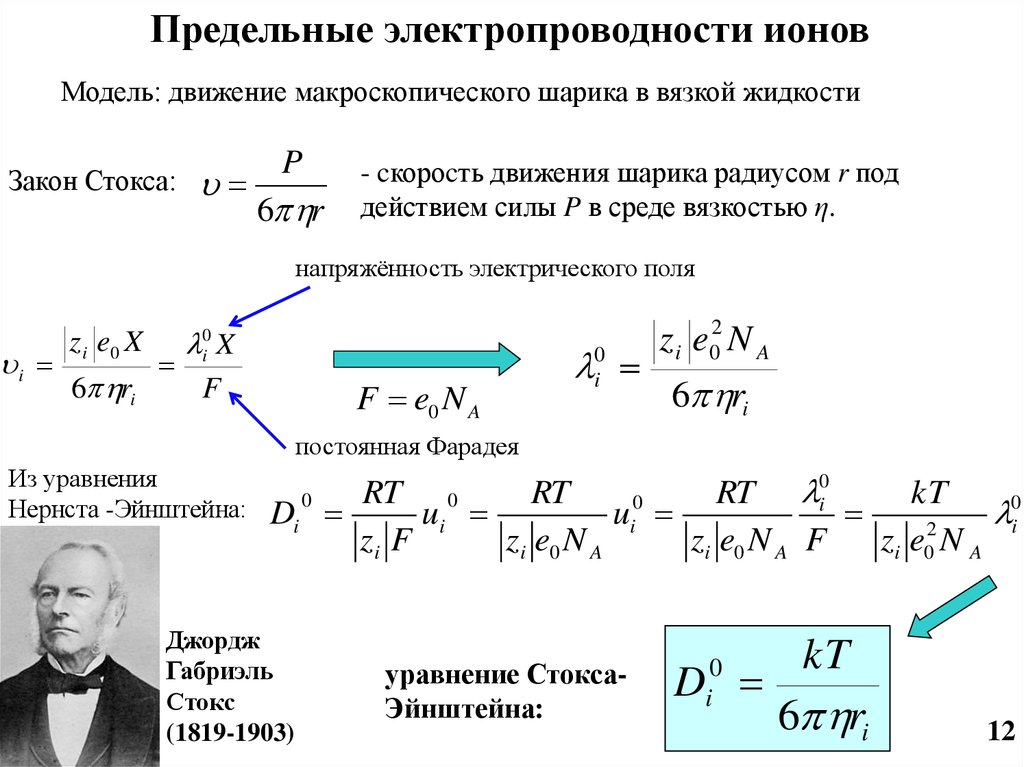
Предельные электропроводности ионовМодель: движение макроскопического шарика в вязкой жидкости
Закон Стокса:
P
6 r
- cкороcть движения шарика радиусом r под
действием силы P в среде вязкостью η.
напряжённость электрического поля
i
z i e0 X
6 ri
X
0
i
F e0 N A
F
0i
z i e02 N A
6 ri
постоянная Фарадея
Из уравнения
Нернста -Эйнштейна:
0
RT 0
RT
RT
kT
0
0
i
Di
ui
ui
i
zi F
zi e0 N A
zi e0 N A F
zi e02 N A
Джордж
Габриэль
Стокс
(1819-1903)
0
уравнение СтоксаЭйнштейна:
kT
D
6 ri
0
i
12
14.
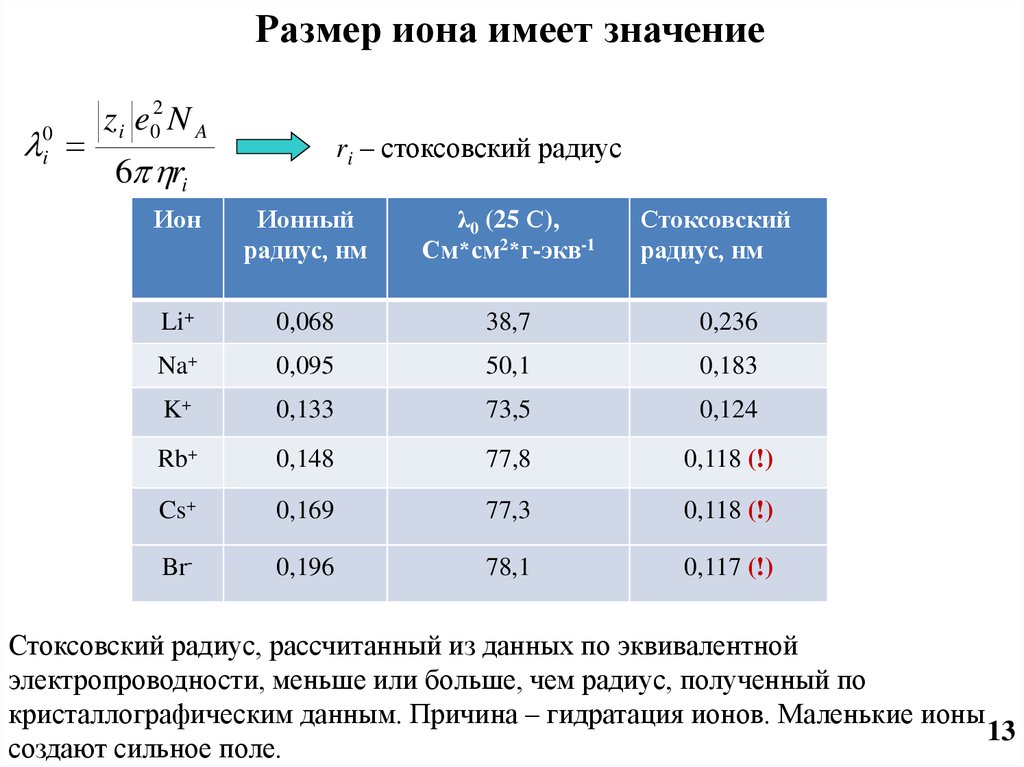
Размер иона имеет значение0i
z i e02 N A
ri – стоксовский радиус
6 ri
Ион
Ионный
радиус, нм
λ0 (25 С),
См*см2*г-экв-1
Стоксовский
радиус, нм
Li+
0,068
38,7
0,236
Na+
0,095
50,1
0,183
K+
0,133
73,5
0,124
Rb+
0,148
77,8
0,118 (!)
Cs+
0,169
77,3
0,118 (!)
Br-
0,196
78,1
0,117 (!)
Стоксовский радиус, рассчитанный из данных по эквивалентной
электропроводности, меньше или больше, чем радиус, полученный по
кристаллографическим данным. Причина – гидратация ионов. Маленькие ионы
13
создают сильное поле.
15.
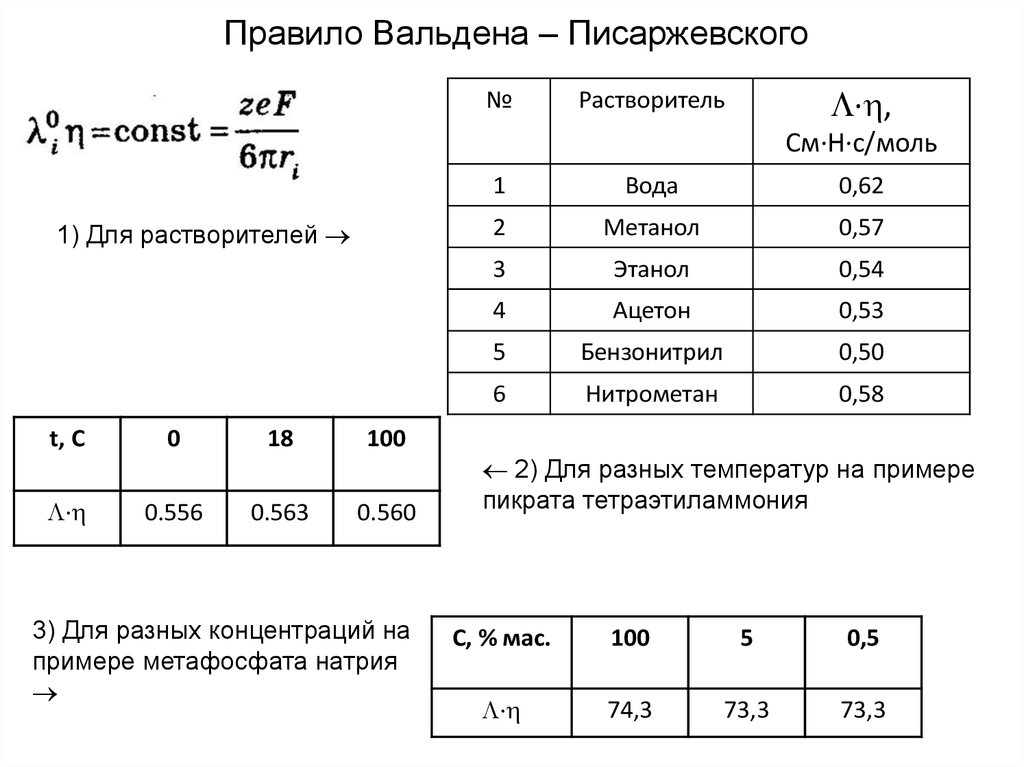
Правило Вальдена – Писаржевского№
· ,
Растворитель
См·Н·с/моль
1) Для растворителей
t, C
0
18
100
·
0.556
0.563
0.560
3) Для разных концентраций на
примере метафосфата натрия
1
Вода
0,62
2
Метанол
0,57
3
Этанол
0,54
4
Ацетон
0,53
5
Бензонитрил
0,50
6
Нитрометан
0,58
2) Для разных температур на примере
пикрата тетраэтиламмония
C, % мас.
100
5
0,5
·
74,3
73,3
73,3
16.
17.
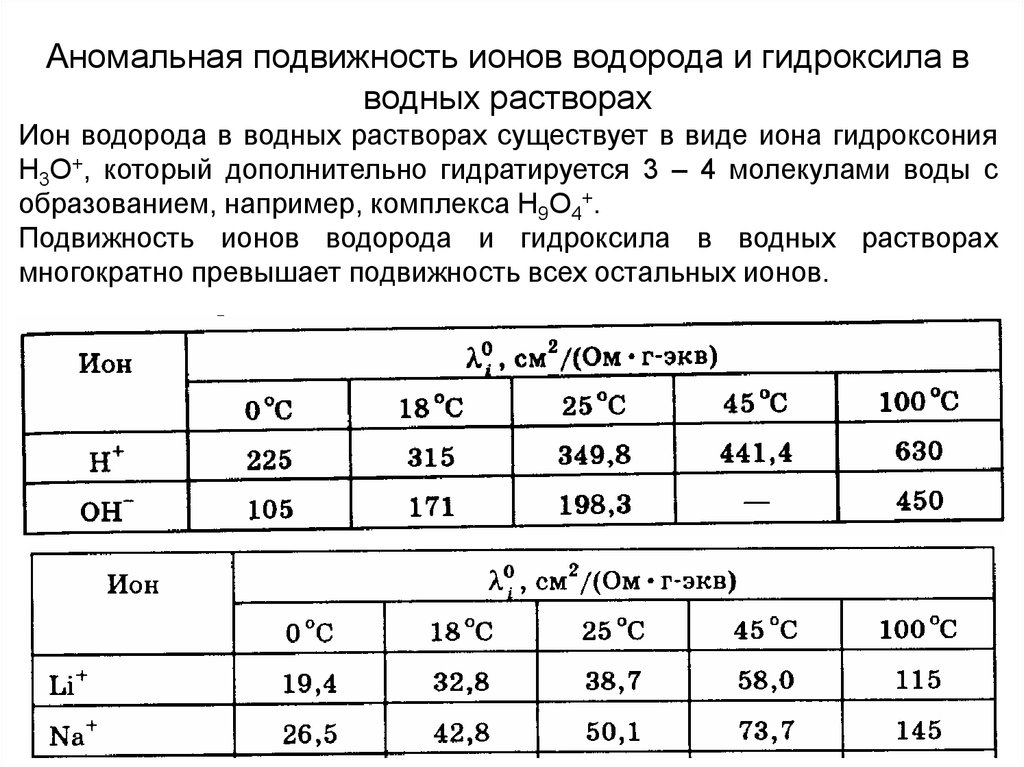
Аномальная подвижность ионов водорода и гидроксила вводных растворах
Ион водорода в водных растворах существует в виде иона гидроксония
H3O+, который дополнительно гидратируется 3 – 4 молекулами воды с
образованием, например, комплекса H9O4+.
Подвижность ионов водорода и гидроксила в водных растворах
многократно превышает подвижность всех остальных ионов.
18.
Объяснение сверхподвижности ионов водорода и гидроксила в водныхрастворах – эстафетный механизм, непосредственный перескок протона
от комплекса гидроксония к соседней молекуле воды (квантовомеханическое протонное туннелирование).
или от молекулы воды на ион гидроксила
Благодаря этому «чемпионами» удельной
электропроводности являются растворы
сильных кислот (tH+ → 1) и щелочей (tOH–
→ 1).
19.
Влияние ионной атмосферы. Электрофоретическийэффект.
Центральный ион и ионная атмосфера заряжены
противоположно. Ионная атмосфера движется
навстречу центральному иону, движение
которого, соответственно, тормозится.
rd
+ - Направление внешнего поля
e02
ni 0 z i2
0 kT
1/ - радиус ионной атмосферы rd
i и атм
zi e02 N A
6 ri
zi e02 N A
6
i zi bэ c
o
i
0
i
zi e02 N A
6
e02
2
0
n
z
i0 i
i zi bэ с
0 kT
e03 N A 10 3 2 N A
где bэ
6
0 kT
Снижение электропроводности центрального иона из-за торможения ионной
атмосферой.
18
20.
Влияние ионной атмосферы. Релаксационный эффект.Причина та же, что и при электрофоретическом
эффекте. Это приводит к смещению центра
ионной атмосферы и, как следствие,
возникновению электростатической силы,
которая стремится вернуть ион назад, и, тем
самым, уменьшает скорость его движения.
i ( oi zi bэ
-
ослабление внешнего электрического поля X-ΔX
X
c ) 1
X
диффузия
X
i zi bэ c
X
первое приближение
разрушение ионной
x 2 2 Di t
o
i
атмосферы за время τ
e0
1
2Di 2 2kTui 2
X
l
1
формула Эйнштейна-Смолуховского
e X
l i ui X 0 2
2kT
e0
le 0
4 0 ( 1 ) 2 4 0
3
0
i
e02
X
X
8 0 kT
l 2kT 2
X
e0
19
21.
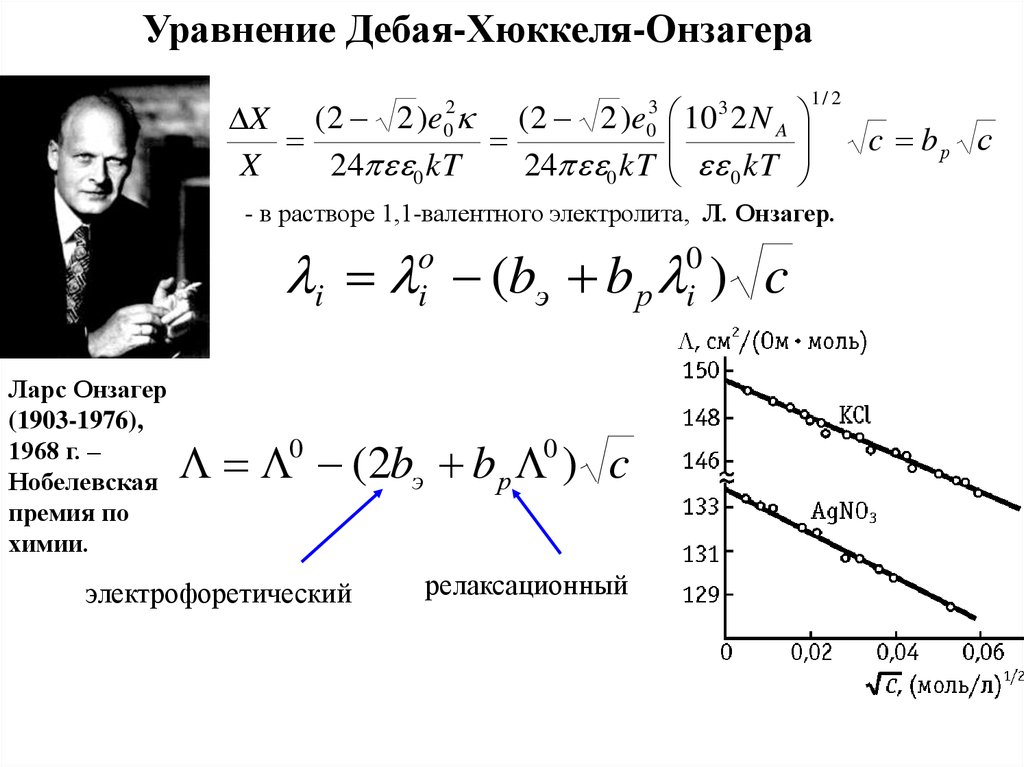
Уравнение Дебая-Хюккеля-ОнзагераX (2 2 )e (2 2 )e
X
24 0 kT
24 0 kT
2
0
3
0
10 2 N A
0 kT
3
1/ 2
- в растворе 1,1-валентного электролита, Л. Онзагер.
i (bэ b р ) c
o
i
Ларс Онзагер
(1903-1976),
1968 г. –
Нобелевская
премия по
химии.
0 (2bэ b р 0 ) c
электрофоретический
релаксационный
0
i
c bр с
22.
Электропроводность. Теория vs. экспериментLars Onsager
Trans. Faraday Soc., 1927, 23, 341-349
20
23.
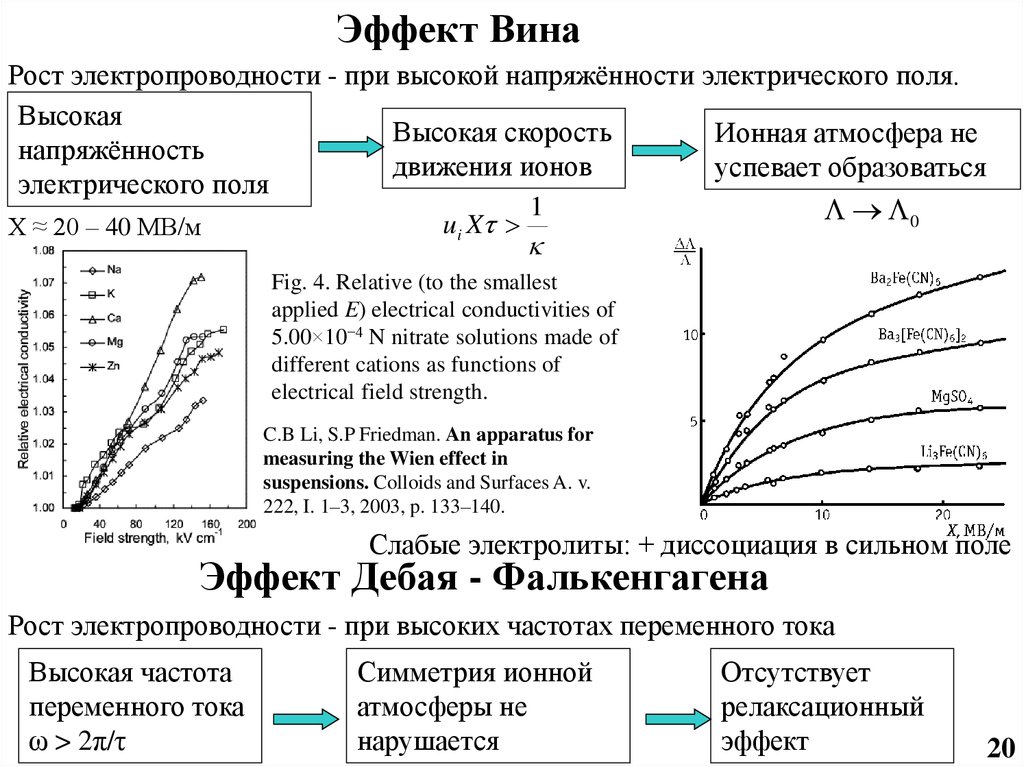
Эффект ВинаРост электропроводности - при высокой напряжённости электрического поля.
Высокая
Высокая скорость
Ионная атмосфера не
напряжённость
движения ионов
успевает образоваться
электрического поля
1
0
ui X
X ≈ 20 – 40 МВ/м
Fig. 4. Relative (to the smallest
applied E) electrical conductivities of
5.00×10−4 N nitrate solutions made of
different cations as functions of
electrical field strength.
C.B Li, S.P Friedman. An apparatus for
measuring the Wien effect in
suspensions. Colloids and Surfaces A. v.
222, I. 1–3, 2003, p. 133–140.
Слабые электролиты: + диссоциация в сильном поле
Эффект Дебая - Фалькенгагена
Рост электропроводности - при высоких частотах переменного тока
Высокая частота
переменного тока
ω > 2π/τ
Симметрия ионной
атмосферы не
нарушается
Отсутствует
релаксационный
эффект
20
24.
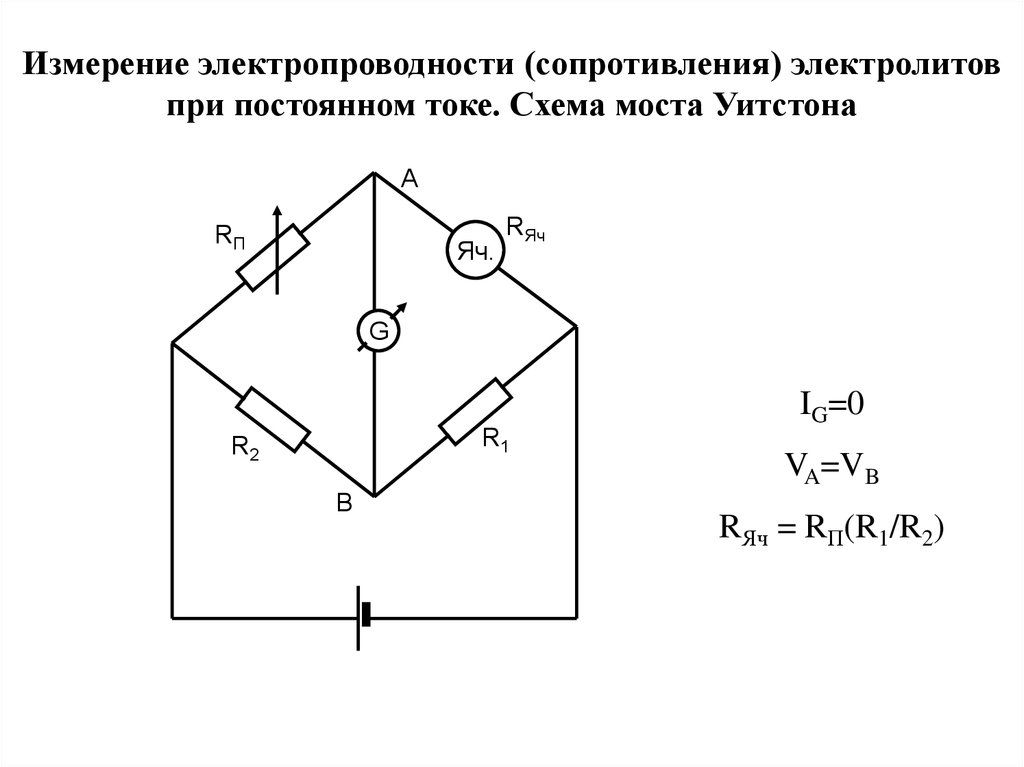
Измерение электропроводности (сопротивления) электролитовпри постоянном токе. Схема моста Уитстона
А
RП
Яч.
RЯч
G
IG=0
R1
R2
В
VA=VB
RЯч = RП(R1/R2)
25.
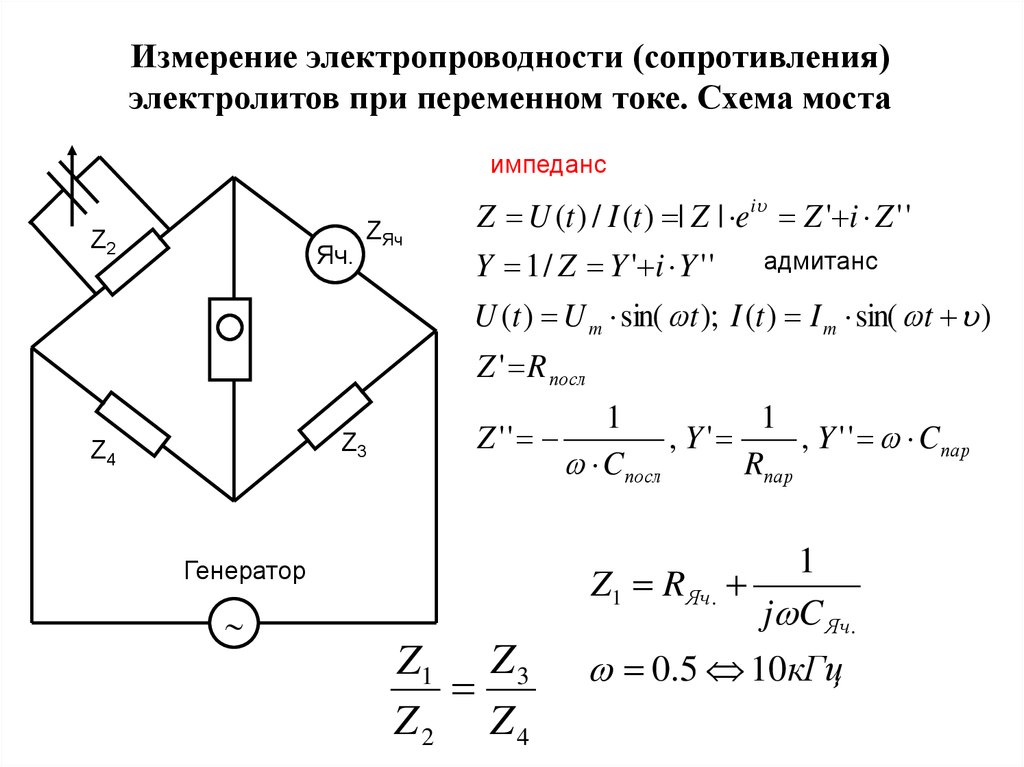
Измерение электропроводности (сопротивления)электролитов при переменном токе. Схема моста
импеданс
Z2
Яч.
ZЯч
Z U (t ) / I (t ) | Z | e i Z ' i Z ' '
Y 1 / Z Y ' i Y ' '
адмитанс
U (t ) U m sin( t ); I (t ) I m sin( t )
Z ' R посл
Z3
Z4
Z ''
1
1
, Y '
, Y ' ' Cпар
Cпосл
Rпар
1
Z1 RЯч.
j C Яч.
Генератор
Z1 Z 3
Z2 Z4
0.5 10кГц
26.
Импеданс электрода как функция приложенной частоты. Частота, при которойнаблюдается независимость импеданса для Ir-фрактала составляет 0.3 Гц и
700 Гц для гладкого платинового электрода.
Данный метод может быть использован для измерения емкости электрода. В
некоторых случаях такая необходимость существует.
27.
Метод кондуктометрииМетод позволяет изучать свойства растворов электролитов в любых
растворителях, в широком интервале температур, давлений и
концентраций.
Для обеспечения высокой точности измерений сопротивление
растворов должно измеряться с точностью не ниже 0,01%. Для этого
обеспечивают
1) регулирование температуры не ниже 0,1°; 2) устранение
поляризации электродов; 3) применение прецизионной аппаратуры;
Основное уравнение: æ= (1/R)·K
где æ - удельная электропроводность раствора, R - сопротивление,
К – постоянная ячейки.
Постоянную ячейки находят по растворам с известной величиной
электропроводности.
Применяется для прямого определения концентрации электролитов
и в варианте титрования.
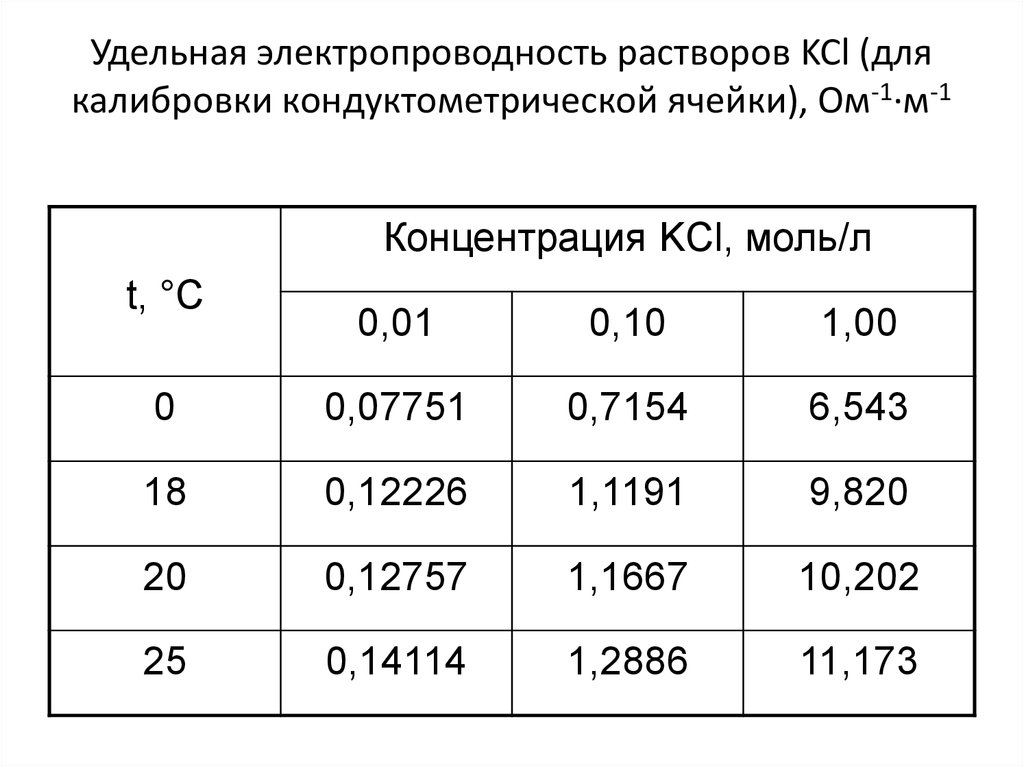
28.
Удельная электропроводность растворов KCl (длякалибровки кондуктометрической ячейки), Ом-1·м-1
Концентрация KCl, моль/л
t, °C
0,01
0,10
1,00
0
0,07751
0,7154
6,543
18
0,12226
1,1191
9,820
20
0,12757
1,1667
10,202
25
0,14114
1,2886
11,173
29.
Примеры применения метода кондуктометрии1. Определение удельной электропроводности воды и
растворителей
2. Определение
электролита
константы
диссоциации
3. Определение
соли
растворимости
слабого
труднорастворимой
4. Определение
константы
устойчивости
и
стехиометрического
состава
комплексных
соединений
5. Измерения в неводных средах
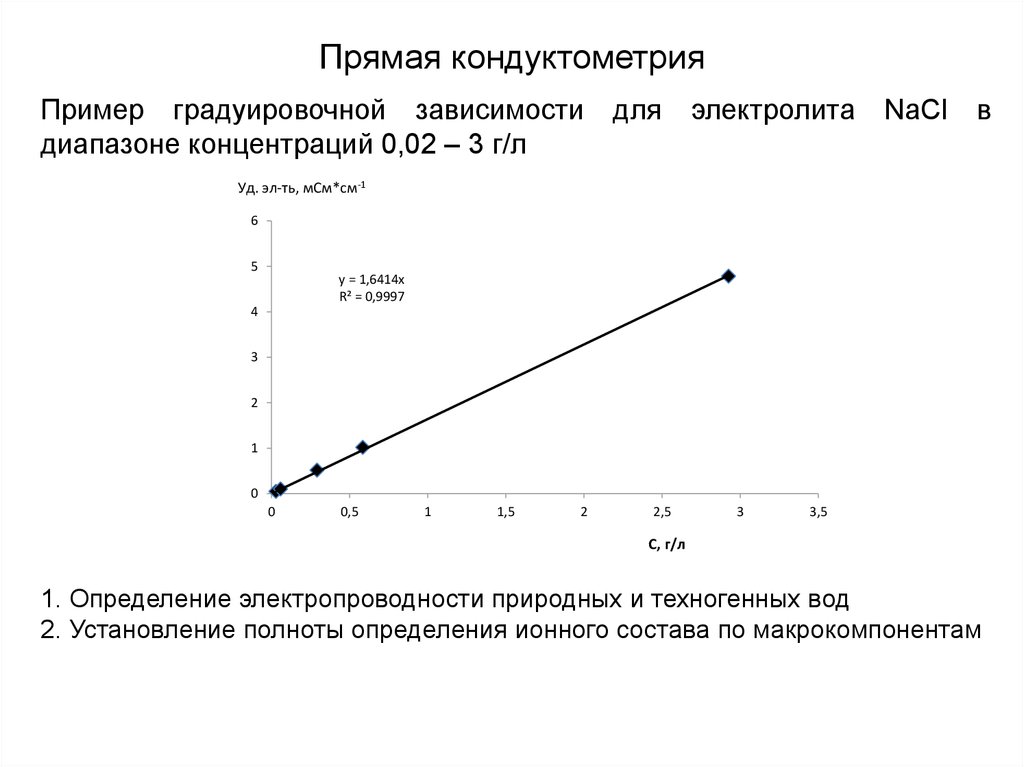
30.
Прямая кондуктометрияПример градуировочной зависимости
диапазоне концентраций 0,02 – 3 г/л
для
электролита
NaCl
в
Уд. эл-ть, мСм*см-1
6
5
y = 1,6414x
R² = 0,9997
4
3
2
1
0
0
0,5
1
1,5
2
2,5
3
3,5
С, г/л
1. Определение электропроводности природных и техногенных вод
2. Установление полноты определения ионного состава по макрокомпонентам
31.
Установление возможности ионизации комплексных соединений по величинамэквивалентной электропроводности их растворов
32.
Λ, См·см2·моль-1Растворитель- вода
2 иона – 100;
3 иона – 230-260;
4 иона – 400
5 ионов - 500
Зависимость от числа ионов, находящихся во внешней сфере: 1 – Pt(NH3)6Cl4;
2 - Pt(NH3)5Cl3; 3 - Pt(NH3)4Cl2; 4 - K2PtCl6; 5 - Pt (NH3)4Cl2; 6 – K[NH3Cl5Pt]; 7 - Pt
(NH3)3Cl; 8 - Pt(H3)2(NH3); 9 – Pt(NH3)2Cl2; 10 - Pt(NH3)2Cl4 при разбавлении V =
1000, кроме кривой 6, где V = 125.
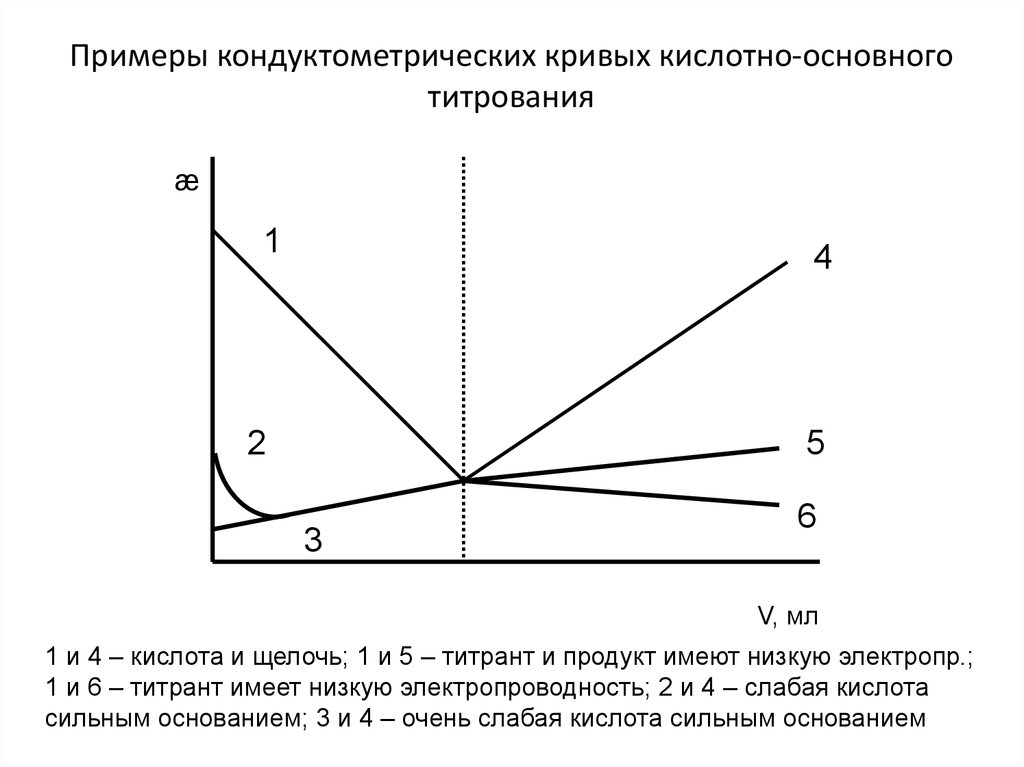
33.
Примеры кондуктометрических кривых кислотно-основноготитрования
æ
1
4
2
5
3
6
V, мл
1 и 4 – кислота и щелочь; 1 и 5 – титрант и продукт имеют низкую электропр.;
1 и 6 – титрант имеет низкую электропроводность; 2 и 4 – слабая кислота
сильным основанием; 3 и 4 – очень слабая кислота сильным основанием



















 Химия
Химия








