Похожие презентации:
Изгиб. Расчет на жесткость
1.
ИзгибРасчет на жесткость
2.
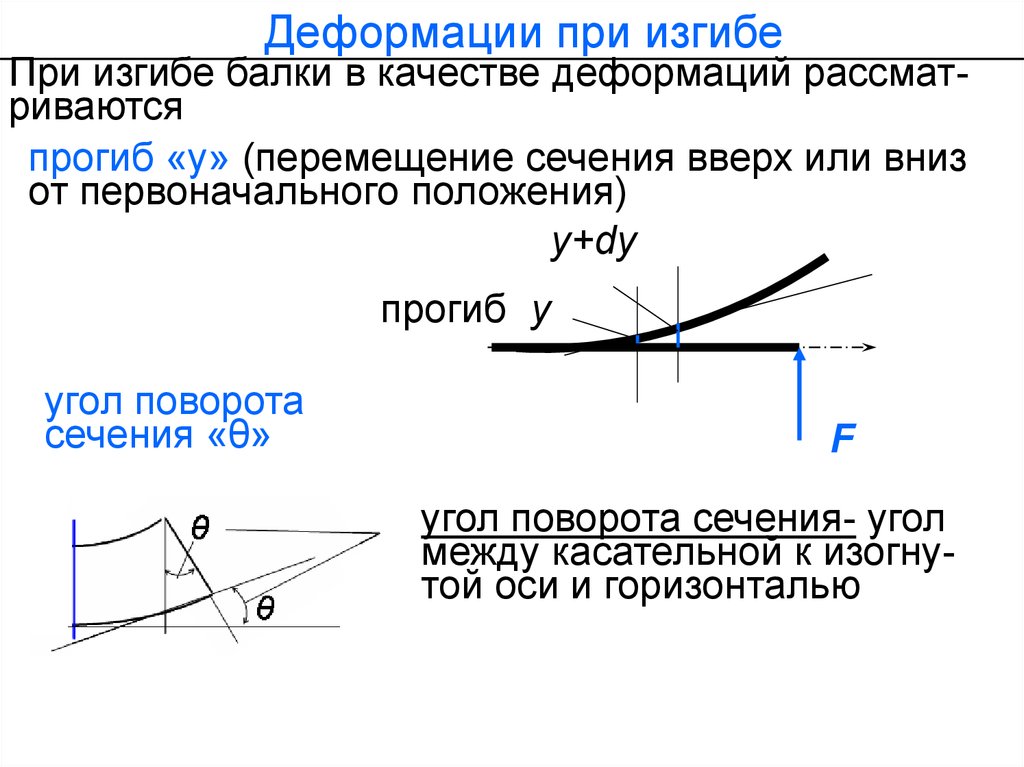
Деформации при изгибеПри изгибе балки в качестве деформаций рассматриваются
прогиб «у» (перемещение сечения вверх или вниз
от первоначального положения)
у+dy
прогиб у
угол поворота
сечения «θ»
F
угол поворота сечения- угол
между касательной к изогнутой оси и горизонталью
3.
Деформации при изгибеИз математики известно уравнение для определения кривизны линии
1
y
k
(1 ( y ) 2 )3/2
В области малых перемещений величиной
можно пренебречь и тогда
1
y
Еy
имеем
и, учитывая
EI x y M
2
(y )
M
y
Ix
уравнение изогнутой оси балки
4.
Деформации при изгибеили в виде
M
y
EI x
Интегрируя уравнение первый раз получают угол
поворота сечения, второй раз – прогиб.
Но при интегрировании необходимо определять
постоянные интегрирования из граничных условий,
которыми являются условия закрепления балки.
5.
Деформации при изгибеИз этих формул сформулированы различные методы определения деформаций.
Для балок постоянной жесткости наиболее часто
используется метод начальных параметров, в
которых в качестве постоянных интегрирования
используется угол поворота в начале координат 0,
и прогиб в начале координат у0.
При этом необходимо выполнять некоторые
приемы при решении.
6.
Деформации при изгибе1. Принимается единое начало координат, помещают его на левом конце балки.
Растояния до точек
у
YB приложения момента,
F
силы и начала нагрузYA
q
b
М ки обозначаются соответственно: a, b, с.
B z
А
c
a
Если нагрузка заканчивается не доходя до рассматриваемого сечения, ее продлевают до сечения.
На участке продления добавляют нагрузку противоположного знака.
7.
Деформации при изгибеУниверсальные уравнения для определения
углов поворота
М( z а )
F( z b )
q( z с )
EIхθ= EI х 0
1!
2!
3!
2
прогибов
3
М ( z а )2
F ( z b )3
q( z с )4
EIхy= EI х y0 EI х 0 z
2!
3!
4!
,
где θ - угол поворота в исследуемом сечении;
у - прогиб в исследуемом сечении;
у0 - прогиб в начале координат;
θ0- угол поворота в начале кoоpдинат;
z- расстояние от начала координат до сечения,
где определяем перемещение;
8.
Прямой поперечный изгиб, определение прогибовметодом начальных параметров.
Для заданной схемы балки требуется:
1. построить эпюры поперечных сил Q и изгибающих
моментов М ;
2. подобрать балку двутаврового сечения из условия
прочности, принимая σadm = 160 МПа;
3. определить жесткость балки, принимая Е = 2·1011Па
4. найти прогиб балки в точке С и D методом
начальных параметров.
9.
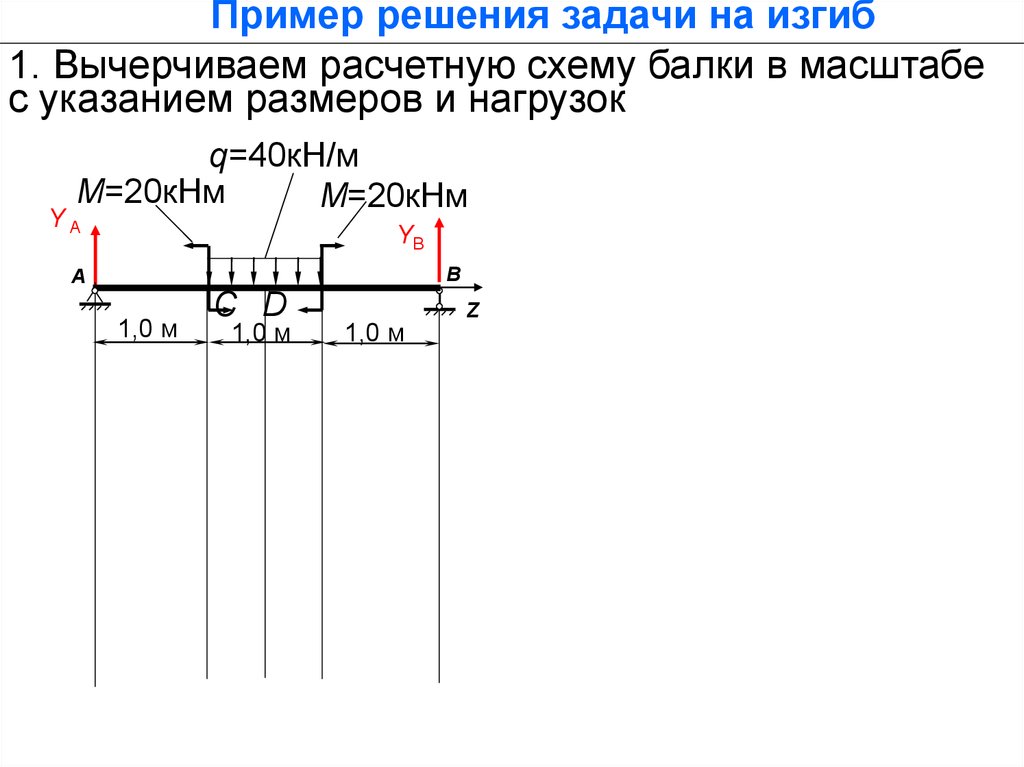
Пример решения задачи на изгиб1. Вычерчиваем расчетную схему балки в масштабе
с указанием размеров и нагрузок
q=40кН/м
М=20кНм
М=20кНм
YА
YВ
В
А
1,0 м
C D
1,0 м
1,0 м
z
10.
2. Определяем реакции, рассматривая условиеравновесия
ΣM(A)= 0; YВ·3 +M-M-q·1·1,5 = 0
YА
А
М=20кНм
М=20кНм
q=40кН/м
YВ
Rq
YВ = q·1·1,5/3=40·0,5=20кН.
YВ = 20 кН.
В
z
1,0 м
1,0 м
1,0 м
ΣM(В)= 0; -YА·3+M-M+q·1·1,5=0;
YА =20 кН
Балка симметричная, реакции
одинаковы.
Проверка
ΣУ =0; YА + YВ - q·1 = 0;
20 + 20 – 40 = 0;
0 = 0.
11.
3. Балка разбивается на участки со своим закономизменения нагрузки
Балку разбиваем на 3 участка
М=20кНм
М=20кНм 2
1-й участок:
Y А=20кН
3
q=40кН/м
1
0 ≤ z1 ≤ 1м
YВ=20кН В
А
z
2-й участок:
1,0 м
1,0 м
1,0 м
1м ≤ z2 ≤ 2 м
Меняем направление оси z ,
помещая начало координат
в точку В
3-й участок:
0 ≤ z3 ≤ 1 м
12.
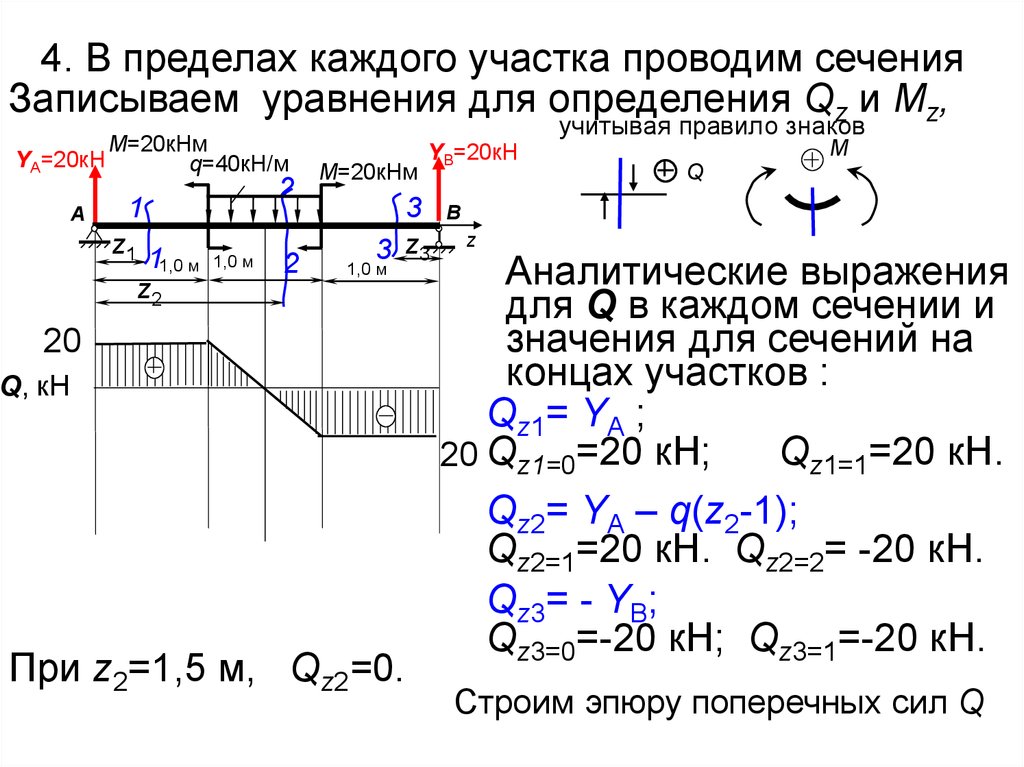
4. В пределах каждого участка проводим сеченияЗаписываем уравнения для определения Qz и Мz,
М=20кНм
YА=20кН
q=40кН/м
А
2
1
z1 1
1,0 м
z2
1,0 м
2
М=20кНм
YВ=20кН
3
3 z3
1,0 м
20
Q, кН
При z2=1,5 м, Qz2=0.
учитывая правило знаков
M
Q
В
z
Аналитические выражения
для Q в каждом сечении и
значения для сечений на
концах участков :
Qz1= YА ;
Qz1=1=20 кН.
20 Qz1=0=20 кН;
Qz2= YА – q(z2-1);
Qz2=1=20 кН. Qz2=2= -20 кН.
Qz3= - YВ;
Qz3=0=-20 кН; Qz3=1=-20 кН.
Строим эпюру поперечных сил Q
13.
MYА=20кН
М=20кНм
q=40кН/м
2
А
М=20кНм
3
1
z1 1
z2
3
1,0 м 1,0 м
2
1,0 м
z3
YВ=20кН
В
Аналитические выражения
z
для М в каждом сечении и
значения для сечений на
концах участков :
20
Mz1= YА· z1;
Mz1=0=0; Mz1=1=20 кНм.
20
20
Mz2= YА· z2 - q(z2-1)2/2);
20
5
Mz2=1=20 кНм; Mz2=1,5=5 кНм;
М,кНм
Mz2=2=20 кНм;
Mz3= YВz3;
Mz3=0=0; Mz3=1=20 кНм.
Строим эпюру изгибающих моментов Mz
Q, кН
Опасные сечения - сечения с изгибающим моментом,
равным 20 кНм.
14.
Подбор сеченияПодбор сечения выполняем из условия прочности
при изгибе
откуда
где Wн.о. – момент сопротивления относительно
нейтральной оси, которая в сечении балки совпадает с осью х
м3= 125 см3.
15.
16.
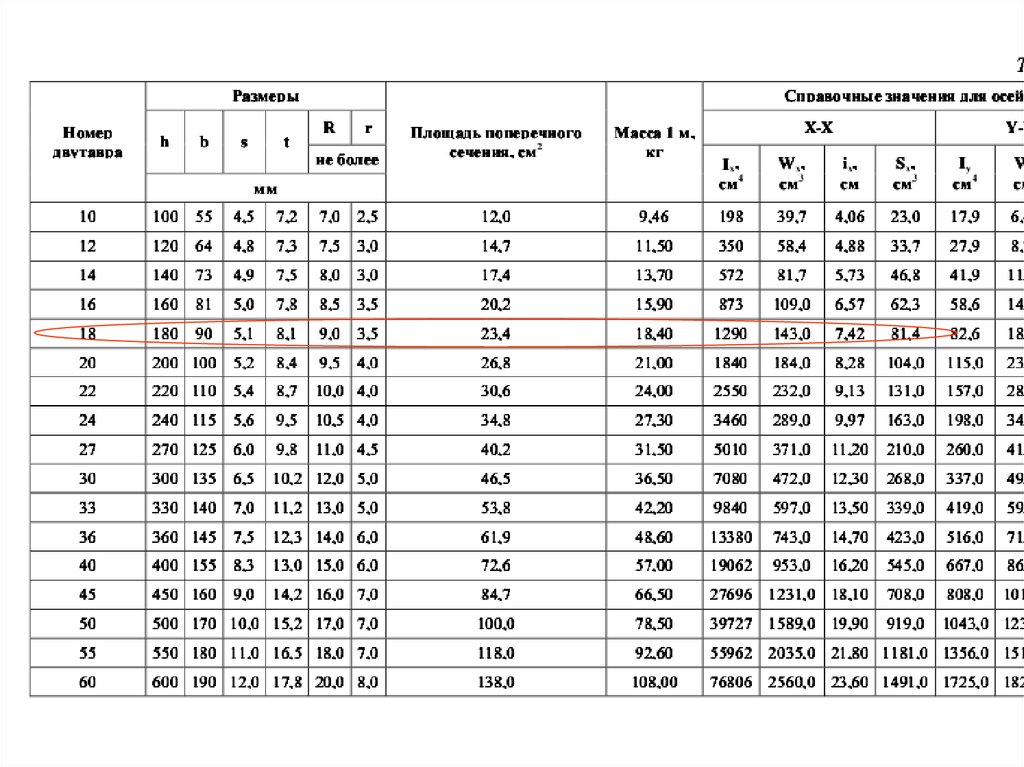
Подбор сечения1) Двутавровый профиль, материал Сталь 3
Ближайшее к полученному значению момента
сопротивления соответствует двутавру № 18,
для которого Wн.о. = 143 см3 .
Жесткость балки с сечением двутавра №18
EIх =2·1011·1290·10-8=2580·103Нм2 =2580кНм2
17.
Пример определения деформаций при изгибеYА=20кН
А
q=40кН/м
YВ=20кН
М
М=20кНм
В
z
C
1,0 м
D
1,0 м
1,0 м
Начало координат в
точке А
В точке А – опора,
поэтому
yА=y0=0
Но угол поворота на опоре не равен 0, поэтому,
чтобы определить θ0, используем второе условие
закрепления.
yВ=0.
18.
Деформации при изгибеYА=20кН
А
q=40кН/м
YВ=20кН
М
М=20кНм
В
z
C
1,0 м
D
1,0 м
1,0 м
Y
кНм2
19.
Деформации при изгибеЕI y ЕI z
x C
x 0 C
YA (z C 0)3
6
zС =1м; EIyС=
м=-3 мм
ЕI y ЕI z
x D
x 0 D
Y A (z D 0)3
6
M (z D 1) 2
2
zD=1,5м
8,9
yD
0,0034 м =-3,4 мм
2580
q(z D 1) 4
24
20.
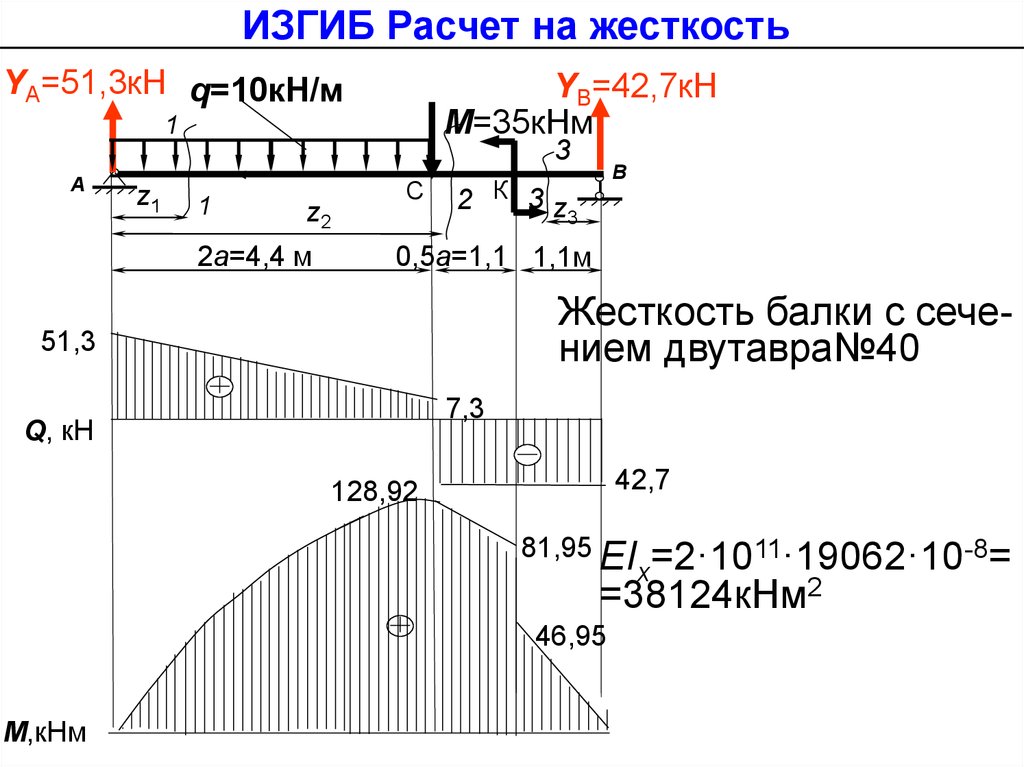
ИЗГИБ Расчет на жесткостьYА=51,3кН q=10кН/м
YВ=42,7кН
М=35кНм
1
3
А
z1
1
z2
2а=4,4 м
С
В
2 К 3z
3
0,5а=1,1 1,1м
Жесткость балки с сечением двутавра№40
51,3
7,3
Q, кН
42,7
128,92
11·19062·10-8=
=2·10
х
=38124кНм2
81,95 EI
46,95
М,кНм
21.
Для определения начальных параметров, а именноθ0 (y0=0), рассмотрим условие закрепления балки
М ( z а )2
F ( z b )3
q( z с )4
EI х y В EI х y0 EI х 0 z
0
2!
3!
4!
0
z- расстояние от начала координат до сечения,
где определяем перемещение
zВ=6,6 м
M ( 6,6 5,5 )2 YA ( 6,6 0 )3 F ( 6,6 4,4 )3 q( 6,6 0 )4 q( 6,6 4,4 )4
EI х y В EI х 0 6,6
0
2
6
6
24
24
35 1,12 51,3 6,6 3 50 2,2 3 10 6,6 4 10 2,2 4
EI х 0 6,6
0
2
6
6
24
24
EI х 0 237 ,5
22.
Для определения прогиба в точке С записываемуравнение прогибов для данного сечения
zС =4,4м
51,3 4,43 10 4,4 4
EI х yС EI х 0 4,4
6
24
1045 728,3 156 ,2 472 ,9кНм 3
472 ,9
yС
0,012м 12 мм
38124
Определяем угол поворота в точке К
zК =5,5м
М( z а )
F ( z b )2
q( z с )3
EIхθК= EI х 0
1!
2!
3!
M ( 5,5 5,5 ) YA ( 5,5 0 )2 F ( 5,5 4,4 )2 q( 5,5 0 )3 q( 5,5 4,4 )3
EI х В EI х 0
1
2
2
6
6
23.
EI х К 237 ,5 775 ,91 30 ,25 277 ,29 2,22 233 ,1EI х К 233,1
233,1
К
0,0061рад 0,35
38124
24.
Прямой поперечный изгиб, определение прогибовметодом начальных параметров.
Для заданной схемы балки требуется:
1. построить эпюры поперечных сил Q и изгибающих
моментов М ;
2. подобрать балку двутаврового сечения из условия
прочности, принимая σadm = 160 МПа;
3. определить жесткость балки, принимая
Е = 2·105 МПа;
4. найти прогибы балки в характерных точках методом
начальных параметров и построить изогнутую ось
балки.
25.
yМ=24кНм
YA=11кН
q=40кН/м
С
A
0,5a
D
a=1 м
YB=69кН
B
0,5a
F=20кН
K
z
Точки С,А,D,В и К
–характерные, в
них определяем
прогиб.
Точки А и В на
опорах: прогиб уА
и уВ равны нулю.
Определение реакций
Составляем уравнения равновесия сил, приложенных
к балке:
ΣМ(А)=0; - М + q· 0,5· 0,25 - q · 1· 0, 5+ YВ· 1- F ·1,5= 0;
YВ· = М+ q· 0,5· 0,75+ F ·1,5=24+15+30=69кН
ΣМ(В)=0;
- М + q· 1,5· 0,75 –YA· 1- F ·0,5= 0;
YА= -М+ q· 1,5· 0,75- F ·0,5=-24+45-10=11кН
ΣУ = 0; YА+ YB– F - q· 1,5 = 0; 11 + 69–20 - 40·1,5 = 0;
80-80=0; 0=0.
26.
y1
Y =69кН
Закрыта
q=40кН/м
отброшенная
часть
Характер наD
B
гружения:
q
z1A
1
0,5a=0,5м
Q, кН
20
М, кНм
5
M
B
YA=11кН
1
С
Q
М=24кНм
a=1 м
0,5a=0,5м
z
K
1
0≤ z1≥0,5 м;
Qz1= - q·z1;
Qz1=0=0;
Qz1=0,5=-20 кН.
Mz1= - qz12/2;
Mz1=0=0; Mz1=0.5=-5 кНм.
27.
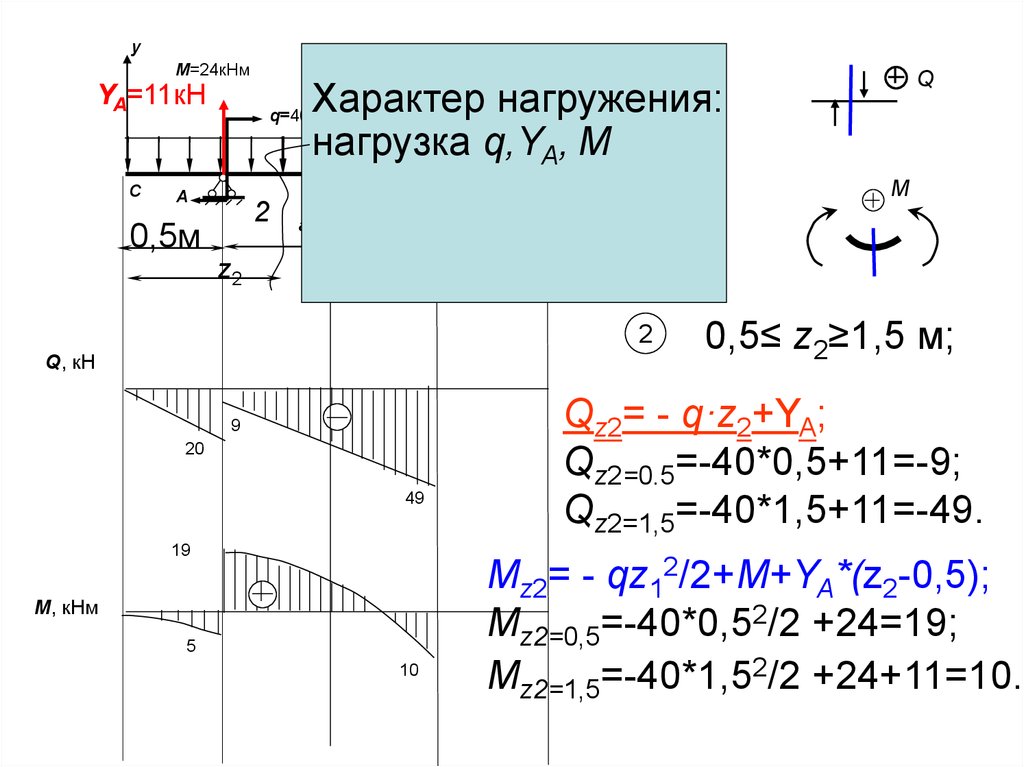
yМ=24кНм
YA=11кН
YB=69кН
Характер нагружения:
нагрузка q,YA, M
q=40кН/м
z
С
Q
D
A
2
0,5м
a=1 м
M
K
B
0,5a=0,5м
z2
2
Q, кН
9
20
49
19
М, кНм
5
10
0,5≤ z2≥1,5 м;
Qz2= - q·z2+YA;
Qz2=0.5=-40*0,5+11=-9;
Qz2=1,5=-40*1,5+11=-49.
Mz2= - qz12/2+M+YA*(z2-0,5);
Mz2=0,5=-40*0,52/2 +24=19;
Mz2=1,5=-40*1,52/2 +24+11=10.
28.
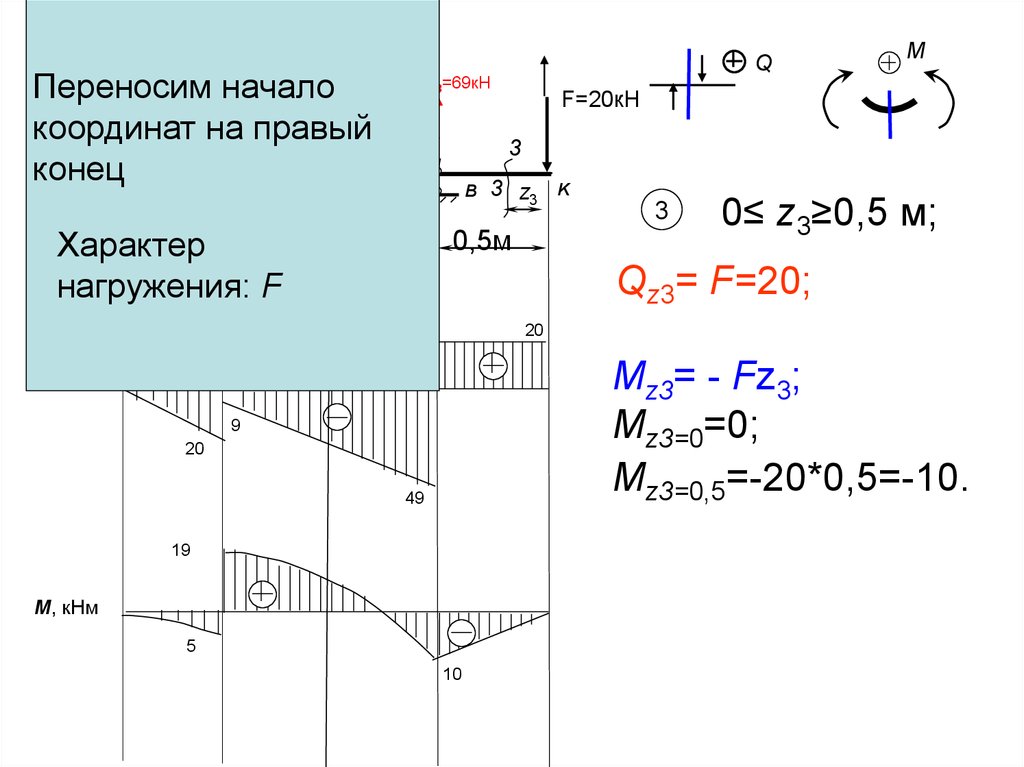
yМ=24кНм
Переносим
начало
V =11кН
q=40кН/м
координат на правый
конец С
D
Q
VB=69кН
F=20кН
A
3
B
A
0,5a=0,5м
Характер
нагружения: F
M
a=1 м
3 z3
0,5м
z
K
3
0≤ z3≥0,5 м;
Qz3= F=20;
20
20
Q, кН
Mz3= - Fz3;
Mz3=0=0;
Mz3=0,5=-20*0,5=-10.
9
20
49
19
М, кНм
5
10
29.
Подбор сеченияПодбираем поперечное сечение по изгибающему
моменту в опасном сечении Mmax =19 кНм из
условия прочности
max
Mx
adm ;
Wx
Mx
Wx
adm
19 10 3
Wx
119 10 6 м 3 119см3
160
По таблице сортамента: Двутавр №18
Жесткость балки
ЕIх=2·1011·1290·10-8=2580·103Нм2=
=2580кНм2.
30.
Определение перемещенийДля построения изогнутой оси балки необходимо
определить прогибы в точках С,D и К
М ( z а )2
F ( z b )3
q( z с )4
EI х y EI х y0 EI х 0 z
2
6
24
у - прогиб в исследуемом сечении;
θ0 - прогиб в начале координат;
у0 - угол поворота в начале координат;
z- расстояние от начала координат до сечения,
для которого определяем перемещение
Начало координат - на левом конце балки,
который не закреплен, поэтому найдем начальные
параметры из условия закрепления балки: на
опорах прогиб равен 0
31.
z А 0,5мq( z А с )4
40( 0,5 0 )4
EI х y А EI х y0 EI х 0 z А
EI х y0 EI х 0 0,5
0
24
24
z В 1,5м
М ( z В 0,5 )2 YA ( z В 0,5 )3 q( z В 0 )4
EI х y В EI х y0 EI х 0 z В
2
6
24
24( 1,5 0,5 )2 11( 1,5 0,5 )3 40( 1,5 0 )4
EI х y0 EI х 0 1,5
0
,
2
6
24
EI х y0 EI х 0 0,5 0,104 0
EI х y0 EI х 0 1,5 12 1,83 8,44 0
EI х 0 EI х С 5,494 кНм
3
EI х y0 EI х yС 2,851кНм
2
32.
2,851yС
0,0011м 1,1мм
2580
Определим прогибы в т. D ( в середине пролета балки между
опорами) и в точке К на конце правой консоли
zD =1,0м
М ( zD 0,5 )2 V A ( zD 0,5 )3 q( z D 0 )4
EI х yD EI х y0 EI х 0 zD
2 2
6 3
24 4
24( 1,0 0,5 ) 11( 1,0 0,5 ) 40( 1,0 0 )
EI х y0 EI х 0 1,0
2
6
24
-2,851 - 5,494 3 0,229 - 1,667 -6,783 кНм 3
6,783
yD
0,0026 м 2,6мм
2580
33.
zК=2,0мМ ( z К 0,5 )2 V A ( z К 0,5 )3 VВ ( z К 1,5 )3
EI х y К EI х y0 EI х 0 z К
2
6
6
q( z К 0 )4 q( z К 1,5 )4
24( 2 0,5 )2 11( 2 0,5 )3 69( 2 1,5 )3
EI х y0 EI х 0 2
24
24
2
6
6
40( 2 0 )4 40( 2 1,5 )4
2,851 5,494 2 27 6,187 1,438 26 ,667 0,104 5,777
24
24
yК
5,777
0,0022 м 2,2мм
2580
Принимая величину допустимого прогиба, равной
0,01l , имеем уadm=0,01·1000=10мм.
Следовательно, условие жесткости балки выполняется.
34.
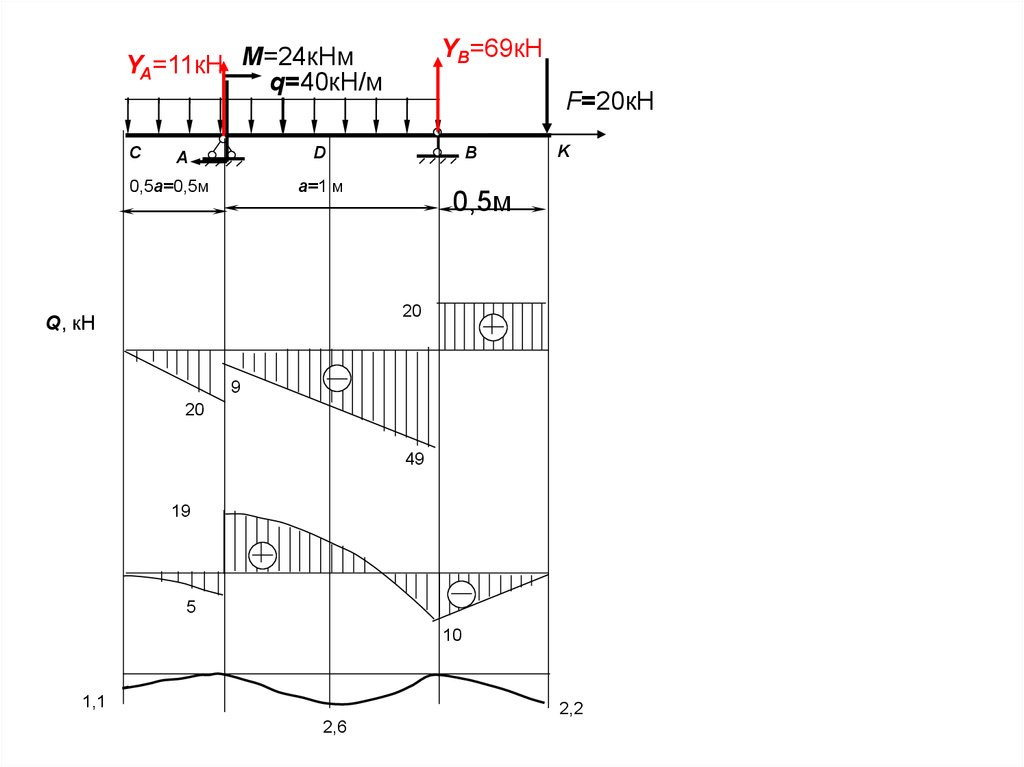
YB=69кНYA=11кН М=24кНм
q=40кН/м
С
F=20кН
D
A
B
a=1 м
0,5a=0,5м
K
0,5м
20
Q, кН
9
20
49
19
5
10
1,1
2,2
2,6























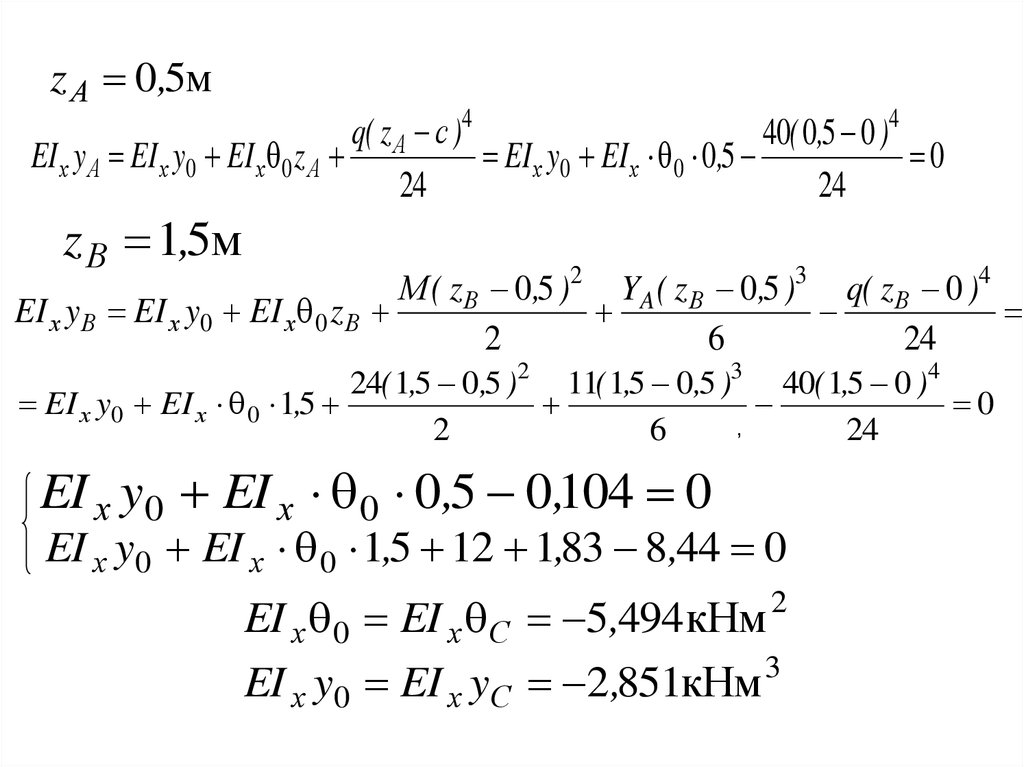


 Физика
Физика








