Похожие презентации:
Решение заданий В9 Многогранники по материалам открытого банка задач ЕГЭ по математике 2013 года
1. Решение заданий В9 многогранники по материалам открытого банка задач ЕГЭ по математике 2013 года
МБОУ СОШ №5 – «Школа здоровья и развития»г. Радужный
Решение заданий
В9
многогранники
по материалам открытого банка
задач ЕГЭ по математике 2013 года
http://mathege.ru/or/ege/main.html
учитель математики Е.Ю. Семёнова
2.
№1Найдите квадрат расстояния между вершинами B и D1
прямоугольного параллелепипеда, для которого AB = 5,
AD = 7, AA1 = 6.
Решение.
С1 Диагональ прямоугольного
D1
параллелепипеда равна
В1
А1
сумме квадратов трех его
измерений:
BD12 = AB2 + BC2 + BB12
BD12 = AB2 + AD2 + AA12
6
BD12 = 52 + 72 + 62 =
7 D
С = 25 + 49 + 36 = 110
А
5
В
Ответ: 110.
3.
№2Найдите расстояние между вершинами A и D1
прямоугольного параллелепипеда, для которого AB = 4,
AD = 12, AA1 = 5.
Решение.
С1 Диагональ грани
D1
прямоугольного
В1
А1
параллелепипеда равна
сумме квадратов двух его
измерений (по теореме
5
Пифагора в п/у ADD1):
2 = AD2 + DD 2
АD
1
1
12 D
С
АD12 = AD2 + AA12
4
АD12 = 122 + 52 = 132
А
В
АD1 = 13
Ответ: 13.
4.
№3Найдите угол AC1C прямоугольного параллелепипеда, для
которого AB = 15, A1D1 = 8, AA1 = 17. Ответ дайте в градусах.
А1
8
С1
D1
В1
17
С
D
А
15
В
Решение.
Угол AC1C найдем из п/у AСС1,
в котором известен катет
СС1 = АА1 = 17, а катет АС
найдем по теореме Пифагора
в п/у AВС:
АС2 = AВ2 + ВС2
AC2 = 152 + 82 = 172
AC = 17. Значит AСС1 − р/б,
AC1C = 45 .
Ответ: 45.
5.
№4В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 41. Найдите расстояние между точками F и B1.
E1
D1
F1
А1
E
В1
D
F
А
41
В
Решение.
Расстояние между точками
F и B1 найдем из п/у FBB1,
С1 в котором известен катет
BB1 = 41, а катет FB является
меньшей диагональю в
правильном шестиугольнике и
равен 41√3. По теореме
Пифагора в п/у FBB1 :
FB1 2 = FВ2 + FB12
С FB 2 = (41√3)2 + 412 =
1
= 412(3 + 1) = 412 ∙ 22;
FB1 = 41 ∙ 2 = 82.
Ответ: 82.
6.
№5В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 29√5. Найдите расстояние между точками A1 и D.
E1
D1
F1
В1
А1
E
D
F
А 29√5
В
Решение.
Расстояние между точками
D и A1 найдем из п/у AA1D,
С1 в котором известен катет
AA1 = 29√5, а катет AD
является большей диагональю в
правильном шестиугольнике и
равен 58√5. По теореме
Пифагора в п/у AA1D :
DA1 2 = DA2 + AA12
С DA 2 = (29√5)2 + (58√5)2 =
1
= 292(5 + 20) = 292 ∙ 52;
DA1 = 29 ∙ 5 = 145.
Ответ: 145.
7.
№6В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 30. Найдите тангенс угла AD1D.
D1
E1
С1
F1
В1
А1
E
D
F
С
А
30
Решение.
Рассмотрим п/у AD1D,
в котором известен катет
DD1 = 30, а катет AD является
большей диагональю в
правильном шестиугольнике
и равен 60.
tg AD1D = AD : DD1 = 60 : 30 = 2
В
Ответ: 2.
8.
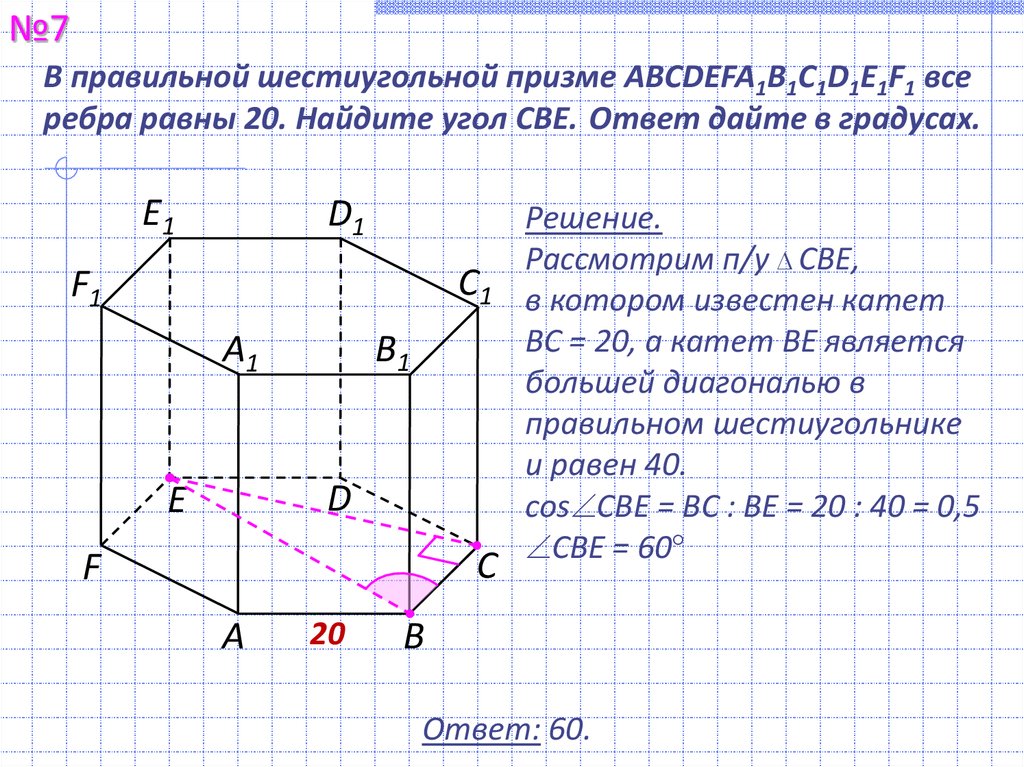
№7В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 20. Найдите угол СВЕ. Ответ дайте в градусах.
E1
D1
С1
F1
В1
А1
D
E
С
F
А
20
Решение.
Рассмотрим п/у СВЕ,
в котором известен катет
ВС = 20, а катет ВЕ является
большей диагональю в
правильном шестиугольнике
и равен 40.
cos СВЕ = ВС : ВЕ = 20 : 40 = 0,5
СВЕ = 60
В
Ответ: 60.
9.
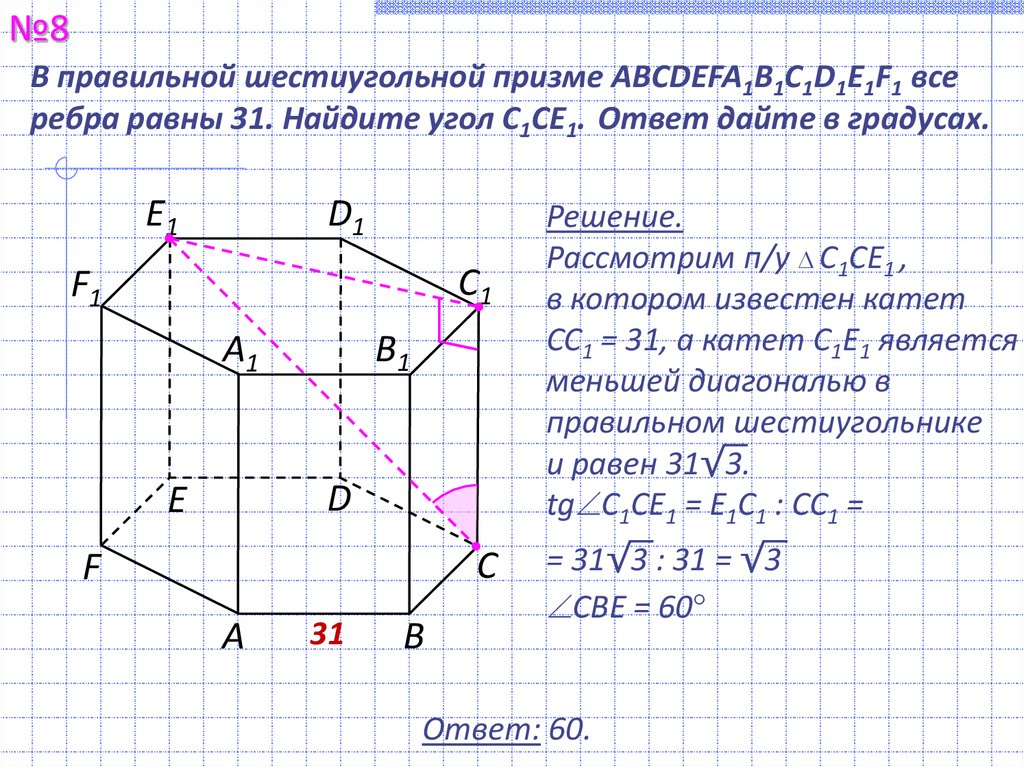
№8В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 31. Найдите угол С1СЕ1. Ответ дайте в градусах.
D1
E1
С1
F1
В1
А1
D
E
С
F
А
31
В
Решение.
Рассмотрим п/у С1СЕ1 ,
в котором известен катет
СС1 = 31, а катет С1Е1 является
меньшей диагональю в
правильном шестиугольнике
и равен 31√3.
tg С1СЕ1 = E1С1 : CC1 =
= 31√3 : 31 = √3
СВЕ = 60
Ответ: 60.
10.
№9Найдите расстояние между вершинами D и В1 многогранника,
изображенного на рисунке. Все двугранные углы многогранника
прямые.
А2 3
В2
D2
2
С2
6
D1
12
А1
С1
Решение.
Рассмотрим п/у В1ВD,
в котором катет
BB1 = 12 – 6 = 6, а катет
BD2 = AD2 + AB2 = 32 + 62 = 45
DB12 = DB2 + BB12 = 45 + 36 = 81
DB1 = 9.
В1
А
D
6
В
С
Ответ: 9.
11.
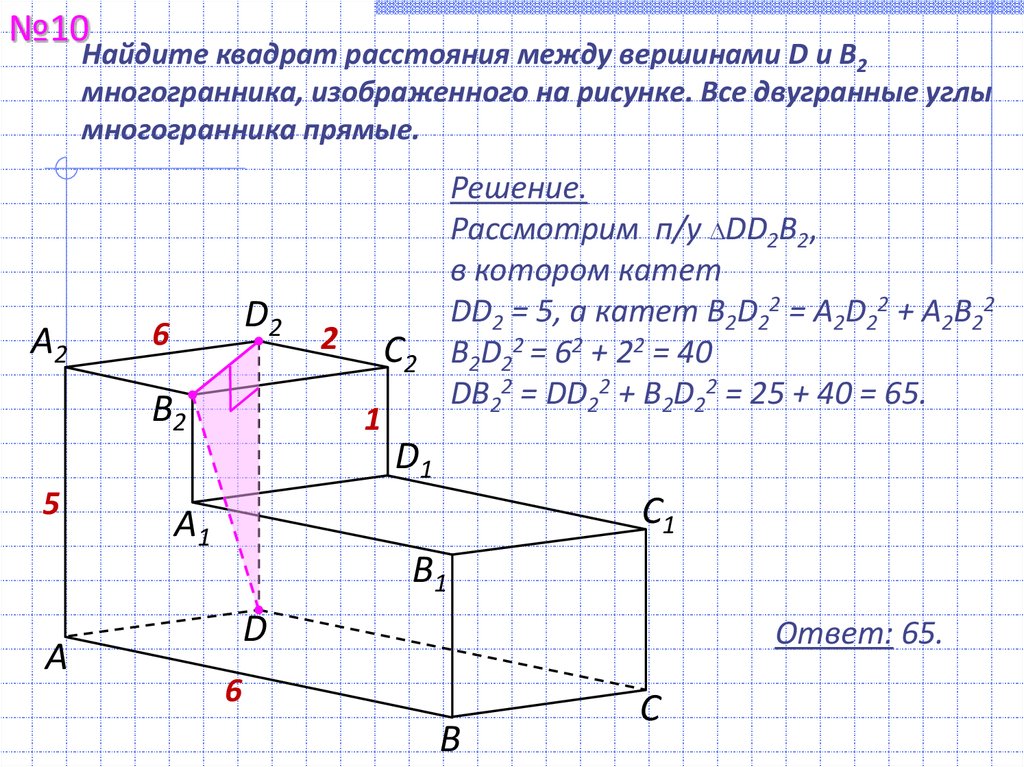
№10Найдите квадрат расстояния между вершинами D и В2
многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
А2
D2
6
В2
2
Решение.
Рассмотрим п/у DD2В2,
в котором катет
DD2 = 5, а катет B2D22 = A2D22 + A2B22
B2D22 = 62 + 22 = 40
DB22 = DD22 + B2D22 = 25 + 40 = 65.
С2
1
D1
5
А
С1
А1
В1
D
Ответ: 65.
6
В
С
12.
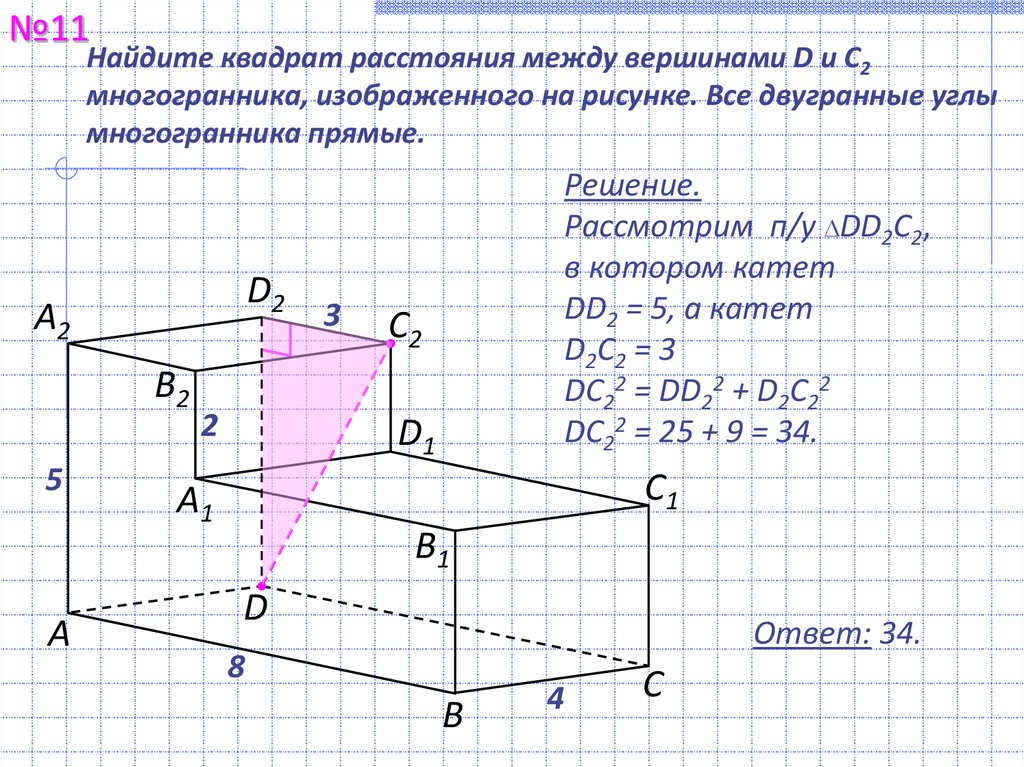
№11Найдите квадрат расстояния между вершинами D и С2
многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
D2
А2
В2
5
А
2
3
Решение.
Рассмотрим п/у DD2С2,
в котором катет
DD2 = 5, а катет
D2С2 = 3
DС22 = DD22 + D2С22
DС22 = 25 + 9 = 34.
С2
D1
С1
А1
В1
D
Ответ: 34.
8
В
4
С
13.
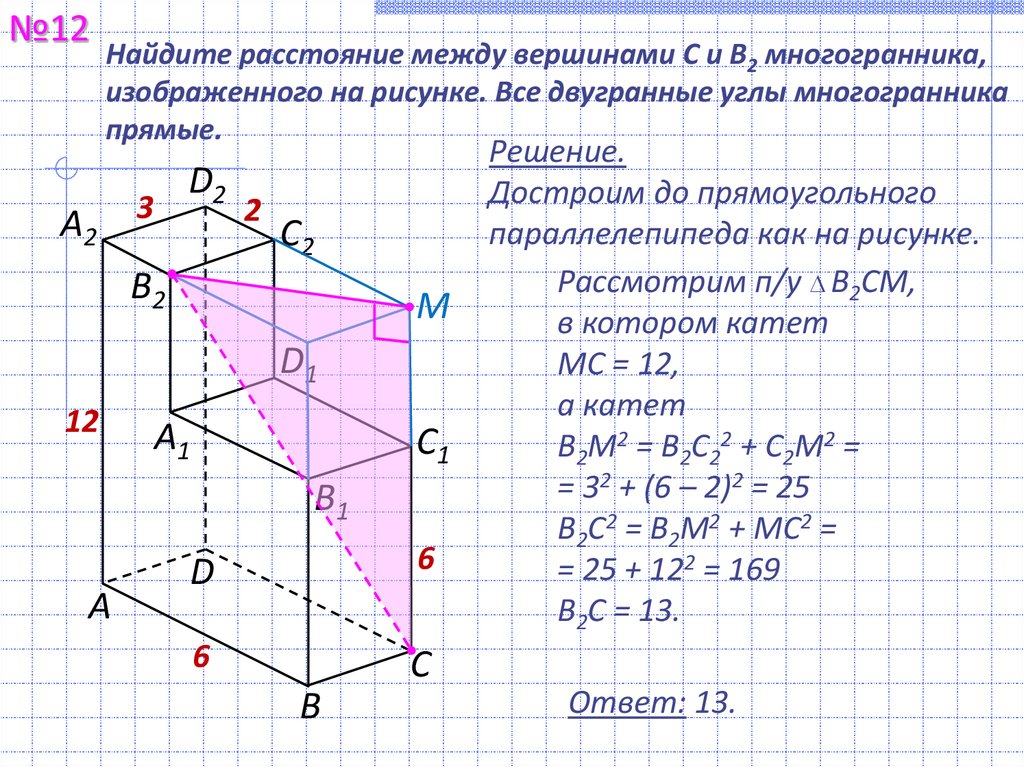
№12Найдите расстояние между вершинами C и B2 многогранника,
изображенного на рисунке. Все двугранные углы многогранника
прямые.
А2 3
D2
2
С2
В2
М
D1
12
А1
С1
В1
А
D
6
6
С
В
Решение.
Достроим до прямоугольного
параллелепипеда как на рисунке.
Рассмотрим п/у B2СМ,
в котором катет
МС = 12,
а катет
B2М2 = B2C22 + C2М2 =
= 32 + (6 – 2)2 = 25
B2C2 = B2M2 + MC2 =
= 25 + 122 = 169
B2C = 13.
Ответ: 13.
14.
№13А2
Найдите квадрат расстояния между вершинами А2 и С1
многогранника, изображенного на рисунке. Все двугранные
углы многогранника прямые.
D2
12
В2
А1
14
D1
В1
D
А
14
7 С
2
В
Решение.
Достроим до прямоугольного
параллелепипеда как на рисунке.
Рассмотрим п/у А2С1М,
М
в котором катет
С1
МС1 = 14 – 12 = 2,
а катет
А2М2 = A2D22 + D2М2 =
12
= 122 + 142 = 340
A2C12 = A2M2 + MC12 =
= 340 + 4 = 344.
С
Ответ: 344.
15. Используемые материалы
• http://mathege.ru/or/ege/Main − Материалы открытогобанка заданий по математике 2013 года










 Математика
Математика