Решение заданий В8 по материалам открытого банка задач ЕГЭ по математике

1. Решение заданий В8 по материалам открытого банка задач ЕГЭ по математике

2.

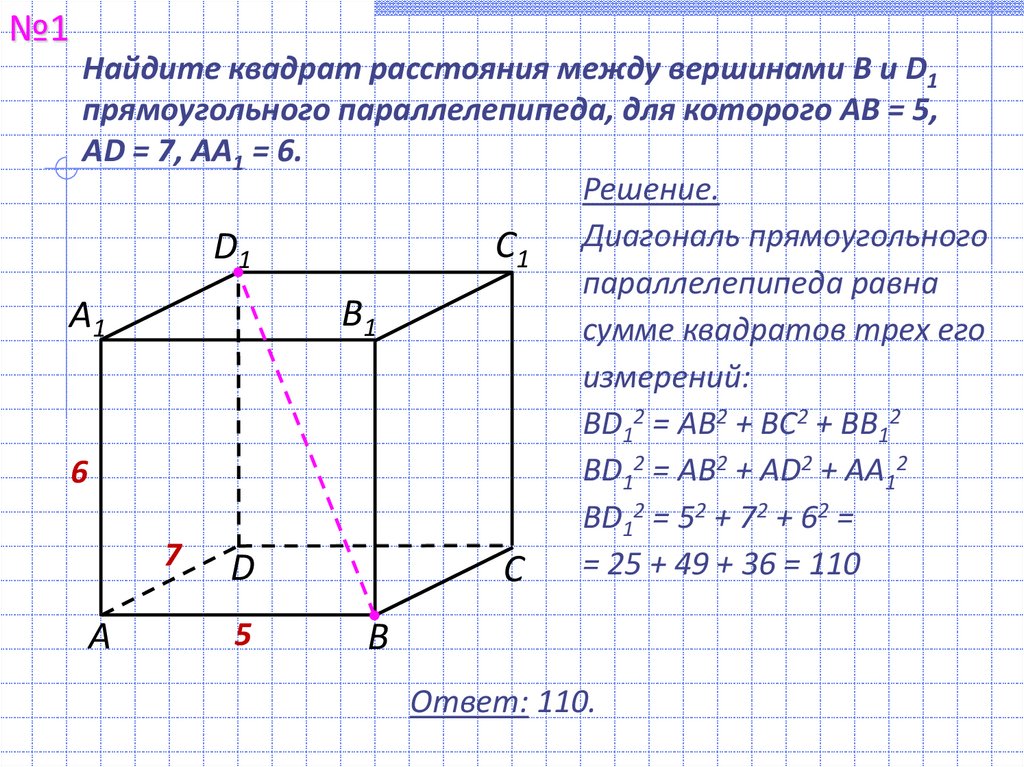
№1
Найдите квадрат расстояния между вершинами B и D1
прямоугольного параллелепипеда, для которого AB = 5,
AD = 7, AA1 = 6.
Решение.
С1 Диагональ прямоугольного
D1
параллелепипеда равна
В1
А1
сумме квадратов трех его
измерений:
BD12 = AB2 + BC2 + BB12
BD12 = AB2 + AD2 + AA12
6
BD12 = 52 + 72 + 62 =
7 D
С = 25 + 49 + 36 = 110
А
5
В
Ответ: 110.

3.

№2
Найдите расстояние между вершинами A и D1
прямоугольного параллелепипеда, для которого AB = 4,
AD = 12, AA1 = 5.
Решение.
С1 Диагональ грани
D1
прямоугольного
В1
А1
параллелепипеда равна
сумме квадратов двух его
измерений (по теореме
5
Пифагора в п/у ADD1):
2 = AD2 + DD 2
АD
1
1
12 D
С
АD12 = AD2 + AA12
4
АD12 = 122 + 52 = 132
А
В
АD1 = 13
Ответ: 13.

4.

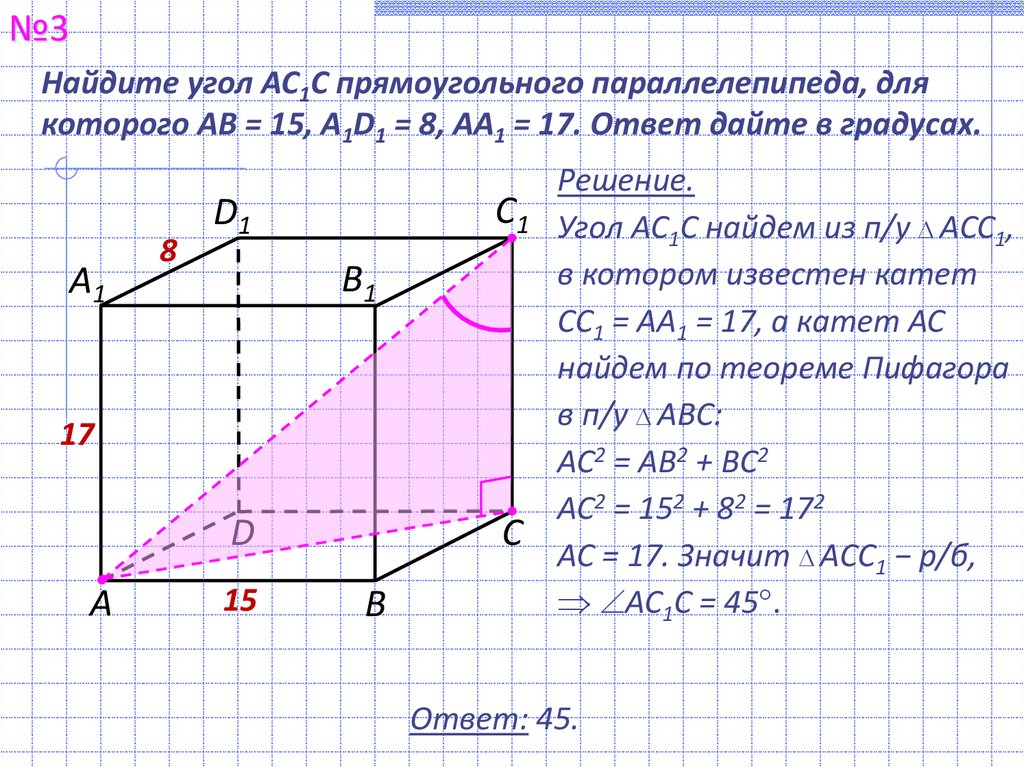
№3
Найдите угол AC1C прямоугольного параллелепипеда, для
которого AB = 15, A1D1 = 8, AA1 = 17. Ответ дайте в градусах.
А1
8
С1
D1
В1
17
С
D
А
15
В
Решение.
Угол AC1C найдем из п/у AСС1,
в котором известен катет
СС1 = АА1 = 17, а катет АС
найдем по теореме Пифагора
в п/у AВС:
АС2 = AВ2 + ВС2
AC2 = 152 + 82 = 172
AC = 17. Значит AСС1 − р/б,
AC1C = 45 .
Ответ: 45.

5.

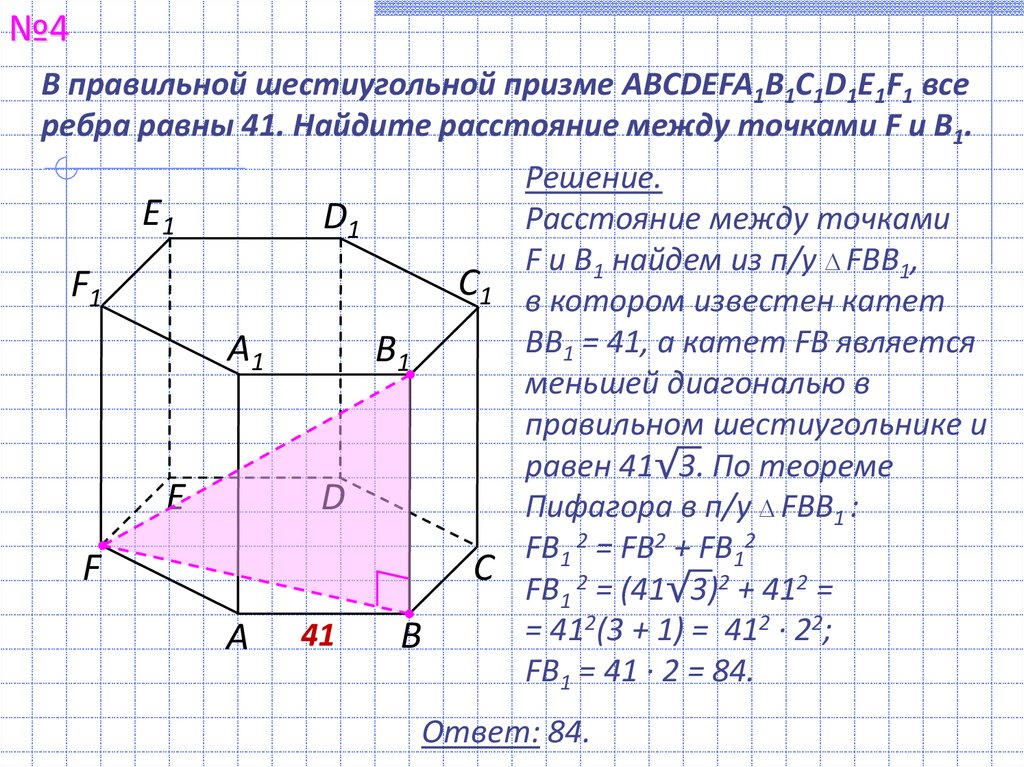
№4
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 41. Найдите расстояние между точками F и B1.
E1
D1
F1
А1
E
В1
D
F
А
41
В
Решение.
Расстояние между точками
F и B1 найдем из п/у FBB1,
С1 в котором известен катет
BB1 = 41, а катет FB является
меньшей диагональю в
правильном шестиугольнике и
равен 41√3. По теореме
Пифагора в п/у FBB1 :
FB1 2 = FВ2 + FB12
С FB 2 = (41√3)2 + 412 =
1
= 412(3 + 1) = 412 ∙ 22;
FB1 = 41 ∙ 2 = 84.
Ответ: 84.

6.

№5
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 29√5. Найдите расстояние между точками A1 и D.
E1
D1
F1
В1
А1
E
D
F
А 29√5
В
Решение.
Расстояние между точками
D и A1 найдем из п/у AA1D,
С1 в котором известен катет
AA1 = 29√5, а катет AD
является большей диагональю в
правильном шестиугольнике и
равен 58√5. По теореме
Пифагора в п/у AA1D :
DA1 2 = DA2 + AA12
С DA 2 = (29√5)2 + (58√5)2 =
1
= 292(5 + 20) = 292 ∙ 52;
DA1 = 29 ∙ 5 = 145.
Ответ: 145.

7.

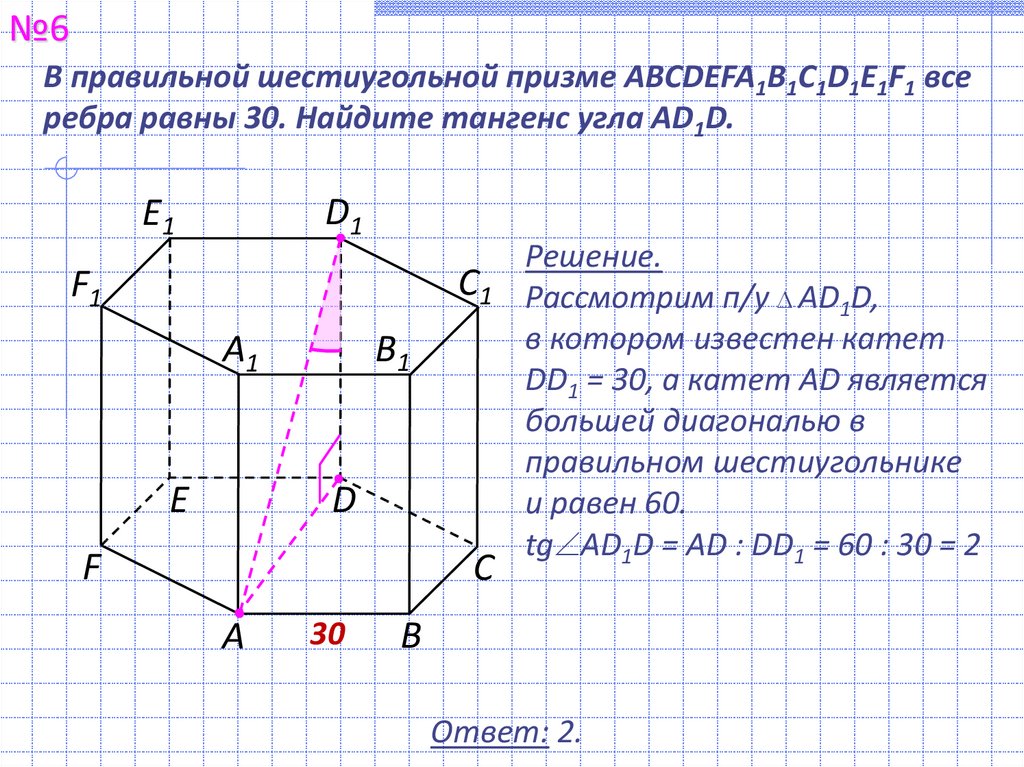
№6
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 30. Найдите тангенс угла AD1D.
D1
E1
С1
F1
В1
А1
E
D
F
С
А
30
Решение.
Рассмотрим п/у AD1D,
в котором известен катет
DD1 = 30, а катет AD является
большей диагональю в
правильном шестиугольнике
и равен 60.
tg AD1D = AD : DD1 = 60 : 30 = 2
В
Ответ: 2.

8.

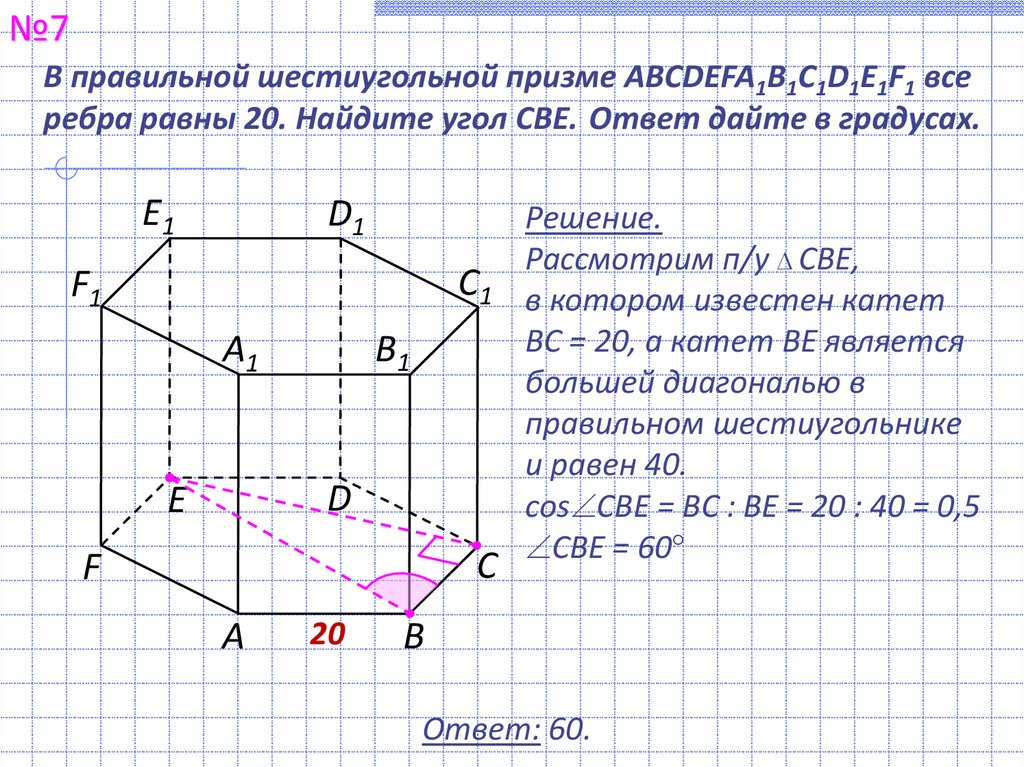
№7
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 20. Найдите угол СВЕ. Ответ дайте в градусах.
E1
D1
С1
F1
В1
А1
D
E
С
F
А
20
Решение.
Рассмотрим п/у СВЕ,
в котором известен катет
ВС = 20, а катет ВЕ является
большей диагональю в
правильном шестиугольнике
и равен 40.
cos СВЕ = ВС : ВЕ = 20 : 40 = 0,5
СВЕ = 60
В
Ответ: 60.

9.

№8
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 31. Найдите угол С1СЕ1. Ответ дайте в градусах.
D1
E1
С1
F1
В1
А1
D
E
С
F
А
31
В
Решение.
Рассмотрим п/у С1СЕ1 ,
в котором известен катет
СС1 = 31, а катет С1Е1 является
меньшей диагональю в
правильном шестиугольнике
и равен 31√3.
tg С1СЕ1 = E1С1 : CC1 =
= 31√3 : 31 = √3
СВЕ = 60
Ответ: 60.

10.

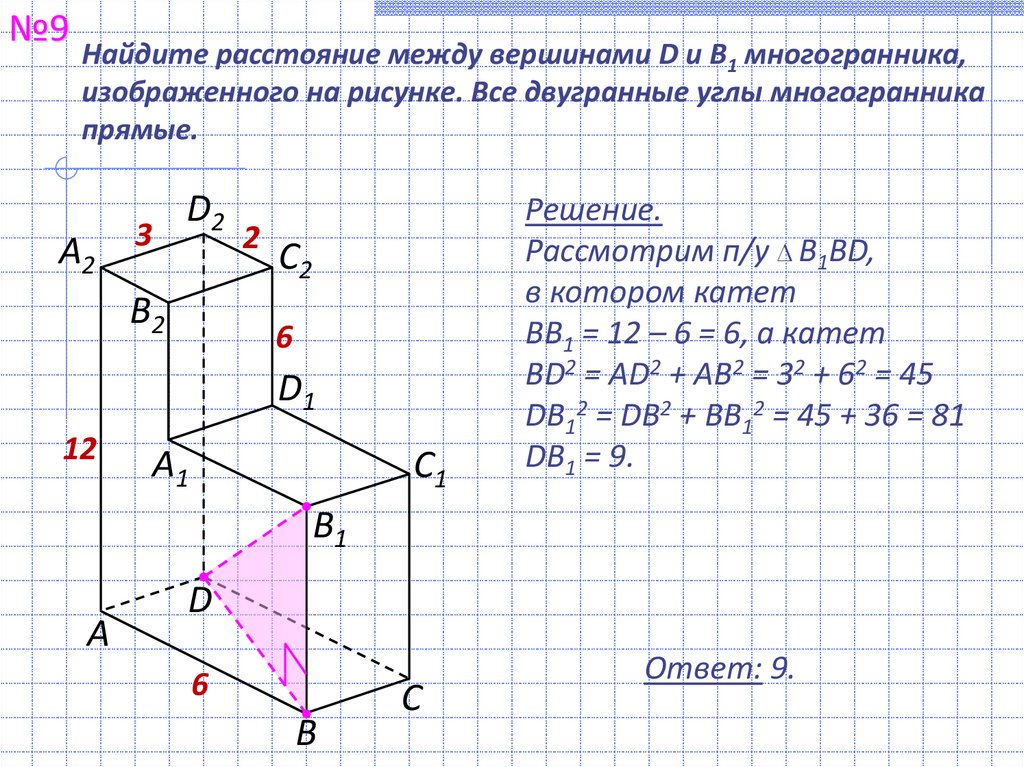
№9
Найдите расстояние между вершинами D и В1 многогранника,
изображенного на рисунке. Все двугранные углы многогранника
прямые.
А2 3
В2
D2
2
С2
6
D1
12
А1
С1
Решение.
Рассмотрим п/у В1ВD,
в котором катет
BB1 = 12 – 6 = 6, а катет
BD2 = AD2 + AB2 = 32 + 62 = 45
DB12 = DB2 + BB12 = 45 + 36 = 81
DB1 = 9.
В1
А
D
6
В
С
Ответ: 9.

11.

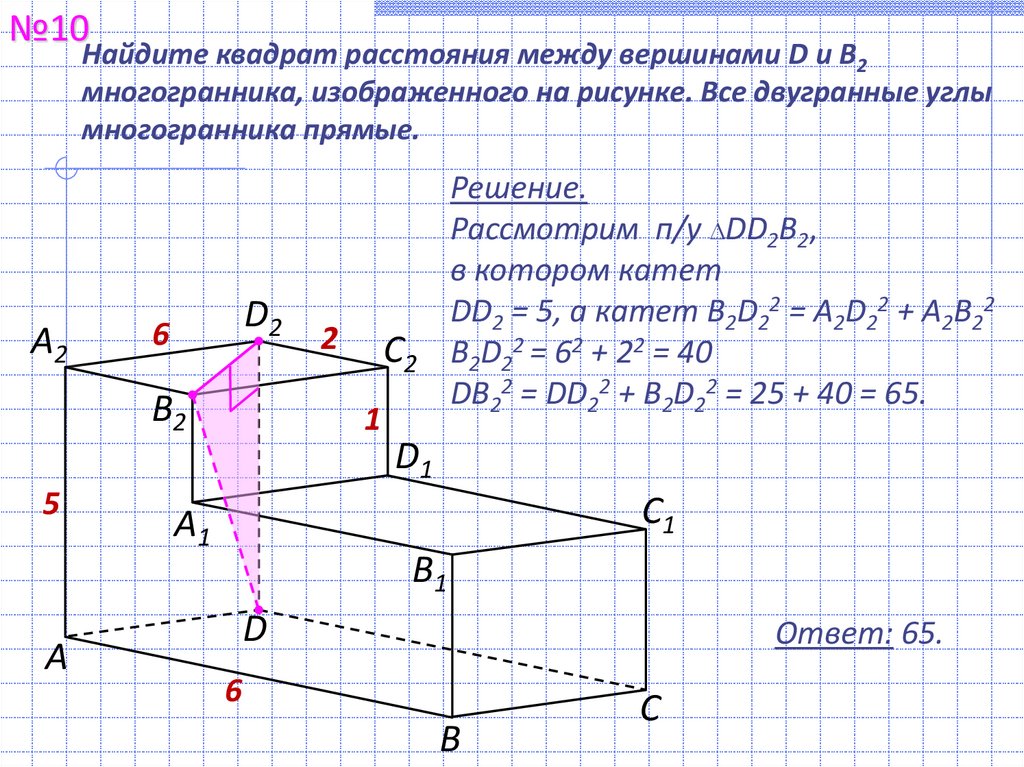
№10
Найдите квадрат расстояния между вершинами D и В2
многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
А2
D2
6
В2
2
Решение.
Рассмотрим п/у DD2В2,
в котором катет
DD2 = 5, а катет B2D22 = A2D22 + A2B22
B2D22 = 62 + 22 = 40
DB22 = DD22 + B2D22 = 25 + 40 = 65.
С2
1
D1
5
А
С1
А1
В1
D
Ответ: 65.
6
В
С

12.

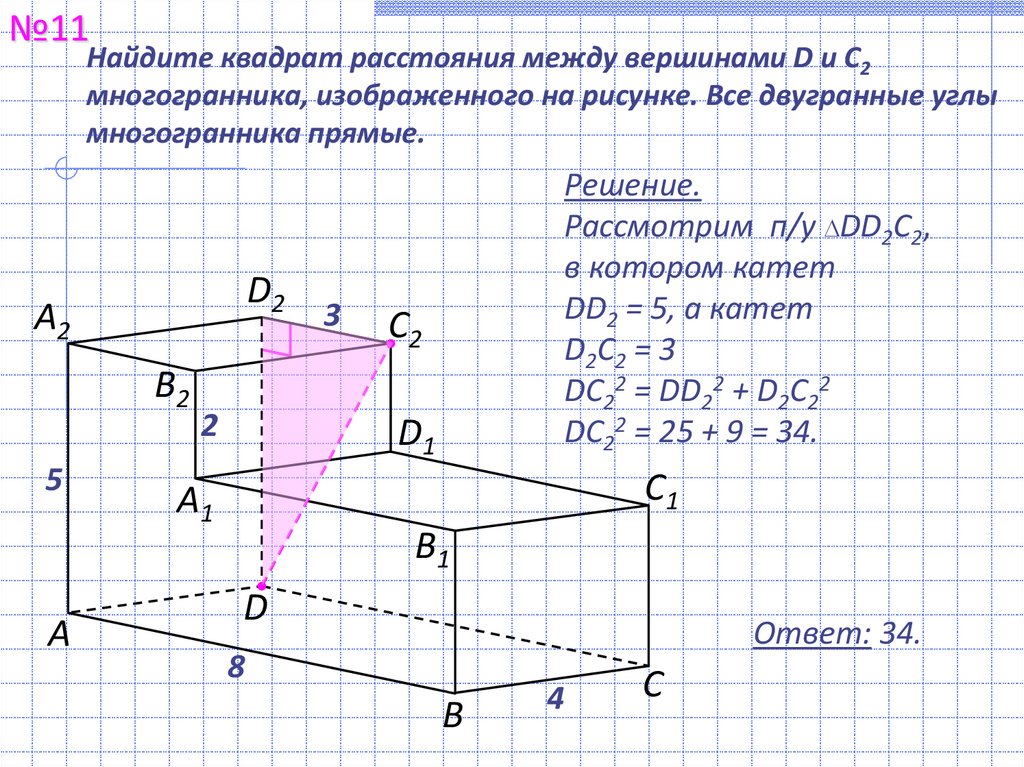
№11
Найдите квадрат расстояния между вершинами D и С2
многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
D2
А2
В2
5
А
2
3
Решение.
Рассмотрим п/у DD2С2,
в котором катет
DD2 = 5, а катет
D2С2 = 3
DС22 = DD22 + D2С22
DС22 = 25 + 9 = 34.
С2
D1
С1
А1
В1
D
Ответ: 34.
8
В
4
С

13.

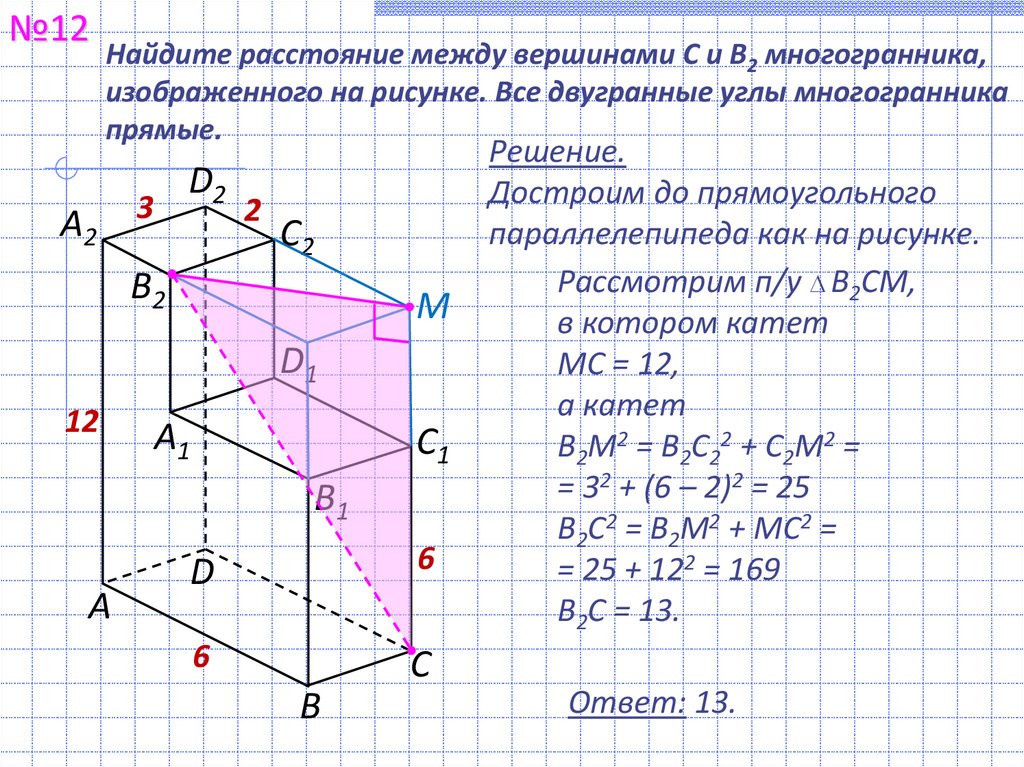
№12
Найдите расстояние между вершинами C и B2 многогранника,
изображенного на рисунке. Все двугранные углы многогранника
прямые.
А2 3
D2
2
С2
В2
М
D1
12
А1
С1
В1
А
D
6
6
С
В
Решение.
Достроим до прямоугольного
параллелепипеда как на рисунке.
Рассмотрим п/у B2СМ,
в котором катет
МС = 12,
а катет
B2М2 = B2C22 + C2М2 =
= 32 + (6 – 2)2 = 25
B2C2 = B2M2 + MC2 =
= 25 + 122 = 169
B2C = 13.
Ответ: 13.

14.

№13
А2
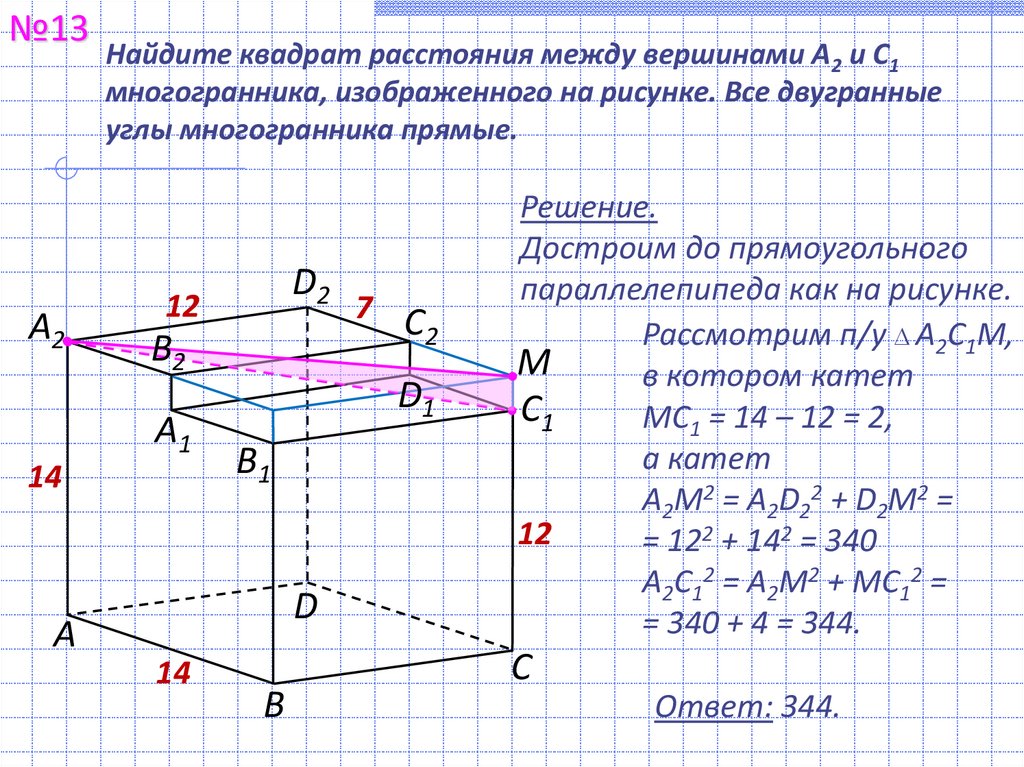
Найдите квадрат расстояния между вершинами А2 и С1
многогранника, изображенного на рисунке. Все двугранные
углы многогранника прямые.
D2
12
В2
А1
14
D1
В1
D
А
14
7 С
2
В
Решение.
Достроим до прямоугольного
параллелепипеда как на рисунке.
Рассмотрим п/у А2С1М,
М
в котором катет
С1
МС1 = 14 – 12 = 2,
а катет
А2М2 = A2D22 + D2М2 =
12
= 122 + 142 = 340
A2C12 = A2M2 + MC12 =
= 340 + 4 = 344.
С
Ответ: 344.

15. Используемые материалы

• http://mathege.ru/or/ege/Main − Материалы открытого
банка заданий по математике 2013 года