Контроль динамических систем АО на основе совместных процедур оптимальной фильтрации и сглаживания полетных данных

1.

7.3 Контроль динамических систем АО на
основе совместных процедур оптимальной
фильтрации и сглаживания полетных
данных

2.

Используя статистические свойства вектора невязок i / N ,
можно построить процедуры контроля и диагностирования ОК по
полетным данным.
Правильному функционированию ОК можно поставить в
i / N
соответствие гауссовский характер вектора невязок
и
допустимые значения диагностического параметра. По аналогии с
таким параметром при функциональном контроле ОК в полете (6.7)
можно сформировать квадратичную форму для послеполетного
анализа состояния ОК по зарегистрированным данным
T
1
J
P
s
(
i)
i/N i
i/N
где
невязок
(7.12)
P
P
P
i
i/i
(
i/i
1
)
N ковариационная матрица для вектора
.
i/N

3.

При правильном функционировании ОК, соответствующем
N
(0
,
P
гауссовскому распределению невязок
i/N
i) , квадратичная
форма
должна иметь
J s (i ) распределение с n степенями свободы
2
(7.13)
J
(
n
,
2
n
)
s(i)
где n – размерность вектора невязок, совпадающая в данном случае с
размерностью вектора состояния ОК.
С учетом статистических свойств распределения
и
2условия
правила
могут быть сформированы необходимые
правильного3
функционирования ДС, т.е. отсутствия сбоев и отказов,
2
J
M
[
J
]
3
D
[
J
]
n
3
2
n (7.14)
s
(
i
) n
s
(
i
)
s
(
i
)
Условие (7.14) характеризует состояние ДС в целом. На
практике, однако, возникает необходимость локализации места
нарушения, т.е. решения задачи диагностирования.

4.

7.4 Диагностирование динамических
систем АО на основе совместных процедур
оптимальной фильтрации и сглаживания
полетных данных

5.

В многомерных динамических системах решение задачи
диагностирования может быть сведено к определению того элемента
вектора состояния (ВС) ОК, с которым наиболее вероятно связано
нарушение. Для построения процедуры диагностирования с
глубиной до элемента ВС необходимо выполнить декомпозицию как
вектора невязок, так и связанного с ним диагностического параметра
(7.12). Это может быть реализовано на основе следующего
ортогонального разложения ковариационной матрицы Pi
, т.е
разложения, сохраняющего норму данной матрицы,
T
(7.15)
P
U
D
U
i
i
i
i
где U i
– верхняя треугольная матрица с единичными
диагональными элементами; Di – диагональная матрица.

6.

С учетом предварительного разложения ковариационной
матрицы (7.15) квадратичную форму (7.12) можно представить в
следующем виде:
2
~
n
i
/
N
(
k
)
T
T
1
1 ~
T
1
~
J
U
D
U
D
(7.16)
s
(
i
)
i
/
N
i
i
i
i
/
N
i
/
N
i
i
/
N
D
k
1
i
(
kk
)
где
1
~
U
i/N
i
i/N
,
T
1T
U
(
U
i
i )
– к - й элемент вектора
;
– к - й диагональный элемент матрицы
~
i / N ( k )
Di (kk )
~
i / N
Di

7.

На основе декомпозиции (7.16) обобщенного параметра (7.12) и с
учетом соотношения (7.14) может быть сформировано необходимое
условие правильного функционирования многомерного ОК по к-му
элементу вектора состояния
2
~
i
/
N
(
k
) 2
J
J
k
3
2
k
s
(
i
/
k
) s
(
i
/
k
1
)
k
D
i
(
kk
)
2
~
i/N
(j)
J
s
(
i/k
1
)
D
где
процедуры;
k
1
j
1
Js(i/0) 0
(7.17)
– эквивалентная запись рекуррентной
i(jj
)
k 1, n

8.

Невыполнение условия (7.17) сигнализирует о наличии
нарушений в ОК по
к-му элементу вектора состояния. Для
распознавания кратковременных сбоев на фоне внезапных или
постепенных отказов могут быть использованы свойства статистики
Фишера Fs (i / k ) . В задачах контроля и диагностирования указанная
ˆ i ( kk )
D
статистика определяется как отношение реальной
и
~
прогнозируемой Di (kk ) дисперсий невязок i / N ( k ) в к - м канале
наблюдений.

9.

ˆ
D
i(kk
)
F
s(i/k)
D
i(kk
)
где
(7.18)
N
1
2
~
ˆ
D
[
]
i
(
kk
)
i
/
N
(
k
/
j
)
i
/
N
(
k
)
N
1
j
1
1N~
i/N
(
k
)
i/N
(
k
/j
)
N
j
1
Fs (i / k ) отражает техническое состояние ОК в i-й
Статистика
момент времени по к-му элементу ВС на заданном временном
интервале, включающем N наблюдений.
Правильному функционированию ОК (отсутствие отказов)
можно поставить в соответствие гауссовское распределение невязки
~
и
распределение статистики Фишера, а
i / N ( k )
2
именно:

10.

если
то
~
N
{
0
,D
},
i
/N
(
k
)
i
(
kk
)
2
F
(a
,b
)
s(i/k
)
где
,
N
а
M
[
F
]
;
s
(
i
/
k
)
N
2
(7.19)
4
N
(
N
1
)
b
D
[
F
]
s
(
i
/
k
)
2
(
N
2
)
(
N
4
)
N – количество данных, используемых для вычисления дисперсии
на скользящем временном интервале.
ˆ
D
i ( kk )
С учетом свойств статистики Фишера (7.19) и правила
может быть сформировано необходимое условие работоспособного
состояния (отсутствие отказов) динамической системы по к - му
элементу ВС
2
F
M
[
F
]
3
D
[
F
]
a
3
b
s
(
i
/
k
) 1
s
(
i
/
k
)
s
(
i
/
k
)

11.

С учетом свойств статистики Фишера (6.27)и правила
может быть сформировано необходимое условие
3
работоспособного состояния (отсутствие отказов) динамической
системы по к- му элементу ВС
2
F
M
[
F
]
3
D
[
F
]
a
3
b
s
(
i
/
k
) 1
s
(
i
/
k
)
s
(
i
/
k
)
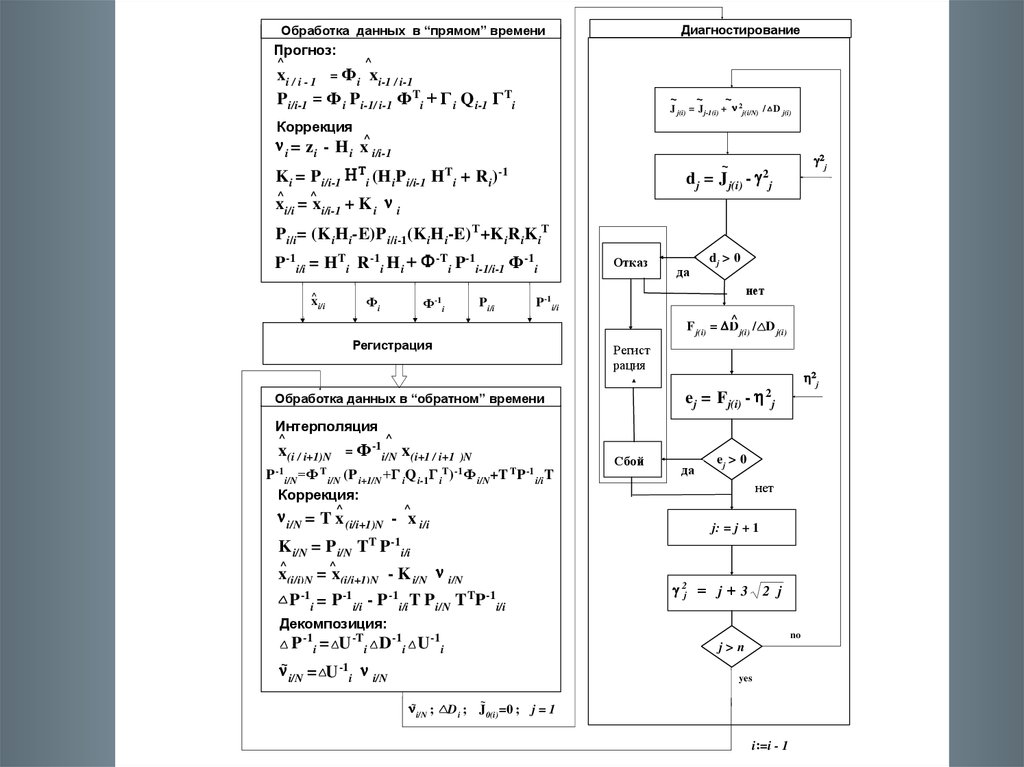
Технология диагностирования динамических систем ОК на
основе совместных процедур оптимальной фильтрации и
сглаживания полетных данных представлена на рисунке.
(7.20)

12.

Диагностирование
Обработка данных в “прямом” времени
Прогноз:
^
^
xi / i - 1 = Ф i x i-1 / i-1
P i/i-1 = Ф i P i-1/ i-1 Ф Ti + Г i Q i-1 Г Ti
~
~
~
J j(i) = J j-1(i) + 2j(i/N) / D j(i)
Коррекция
i = z i - H i x^ i/i-1
~
K i = P i/i-1 i (H iP i/i-1 H Ti + R i)-1
dj = J j(i) -
xi/i = x i/i-1 + K i i
^
2
j
j
^
P i/i= (K iH i-E)P i/i-1(K iH i-E) Т+K iR iK iТ
P -1i/i = H Ti R -1i H i -T i P-1 i-1/i-1 Ф -1i
^
Фi
x i/i
Ф -1i
P i/i
Отказ
да
dj > 0
нет
P-1 i/i
^
F j(i) = D j(i) / D j(i)
Регистрация
Регист
рация
Обработка данных в “обратном” времени
2
e j = Fj(i) -
j
j
Интерполяция
^
^
= Ф -1 i/N
x(i / i+1)N
x(i+1 / i+1
)N
(P i+1/N +Г iQ i-1Г iT) -1 Ф i/N +T TP -1 i/i T
i/N
i/N
Коррекция:
P -1
=Ф T
^
Сбой
да
ej > 0
нет
^
i/N = T x (i/i+1)N - x i/i
j: = j + 1
K i/N = P i/N T T P-1i/i
^
^
x(i/i)N = x(i/i+1)N - K i/N i/N
P -1i = P-1i/i - P -1i/iT P i/N T TP-1i/i
2j j 3
2 j
Декомпозиция:
no
P -1i = U -T i D -1i U -1 i
j>n
~ i/N = U -1i i/N
yes
~i/N ;
~
D i ; J0(i) =0 ; j = 1
i:=i - 1

13.

7.5 Диагностирование одноканальной
ИНС на основе совместных процедур
оптимальной фильтрации и сглаживания

14.

a
a
Контур ДВИ
(эталонная
ИНС)
g
g
+
+
(-)
ap
∫
∫
R
V
V
R
V
Контур
интегральной
коррекции для
реальной ИНС
R
∫
∫
+
(-)
+
p
+
V
R
+
(-)
Z
ОФК
x
Vp

15.

Стохастическая математическая модель одноканальной ИНС
x
(
t
)
A
(
t
)
x
(
t
)
G
(
t
)
(
t
)
T
- вектор ошибок ИНС
x
[
V
a
]
0 g 1
1
0
0
R
A(t) 0 0 1
a
0
0 0
z
(
t
)
V
(
t
)
V
(
t
)= H(t)x(t)+ (t) – наблюдение и его модель
ИНС
ДВИ
0
1
0
1
H
(t)
[1000
] - матрица связи наблюдения с вектором ошибок ИНС
Модель ошибок получена на основе детерминированной модели с учетом моделей
(t )
инструментальных ошибок акселерометра a(t ) и гироскопа
1
a
(
t
)
a
(
t
)
(
t
)
2
/
a
a
a
(t) N(0,1)
1
(
t
)
(
t
)
(
t
)
2
/
где a; – время корреляции ошибок; a; – среднеквадратические значения ошибок

16.

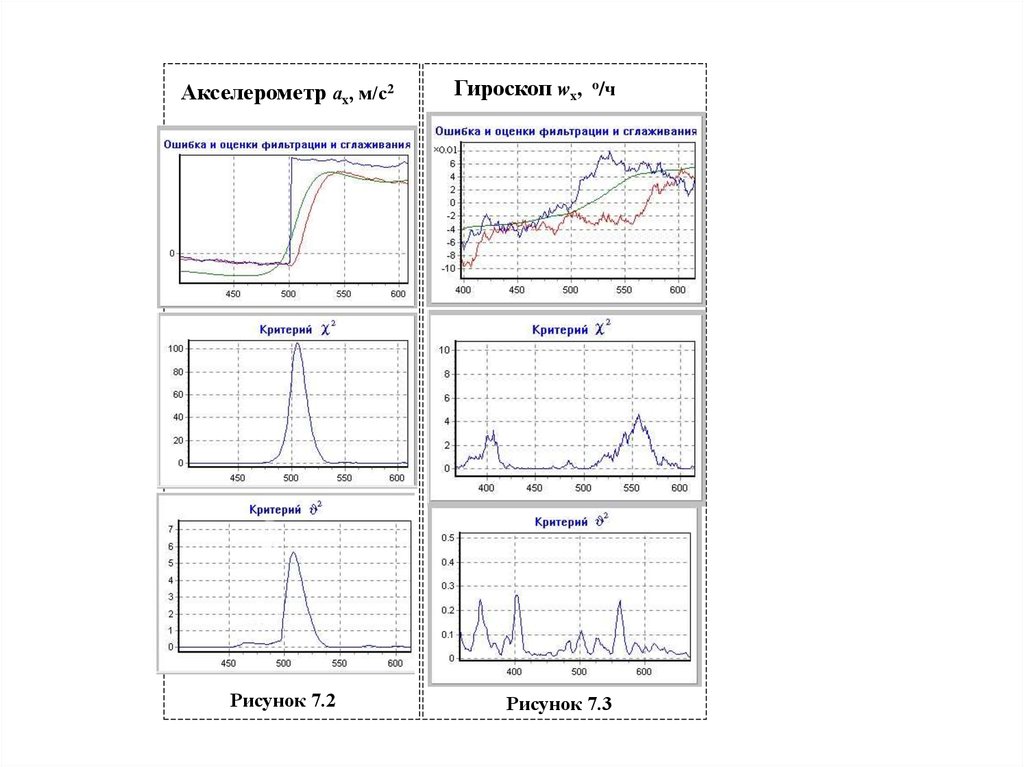
Имитируется отказ акселерометра на 500-й секунде. Такой отказ
косвенно проявляется в процессе фильтрации по каналу скорости,
2
2
когда обобщённый параметр
превышает допуск. При
V V/ j
послеполетной
обработке
зарегистрированных
оценок
и
диагностировании по алгоритму 7.16, представленному на рисунке
из темы 7, определяется, какой из чувствительных элементов ИНС:
акселерометр или гироскоп наиболее вероятно привел к
нарушению. На рисунках 7.2 и 7.3 показана динамика изменения
оценок
соответственно смещения выходного сигнала
акселерометра и дрейфа гироскопа при обработке наблюдений
скорости в «прямом времени» (в полете) и уточнении указанных
оценок в «обратном времени» (после полета) по наблюдению
.
ˆ
ˆ
x
x
i/N
(
i/i
1
)
N
i/i

17.

Акселерометр ах, м/с2
Рисунок 7.2
Гироскоп wх, o/ч
Рисунок 7.3

18.

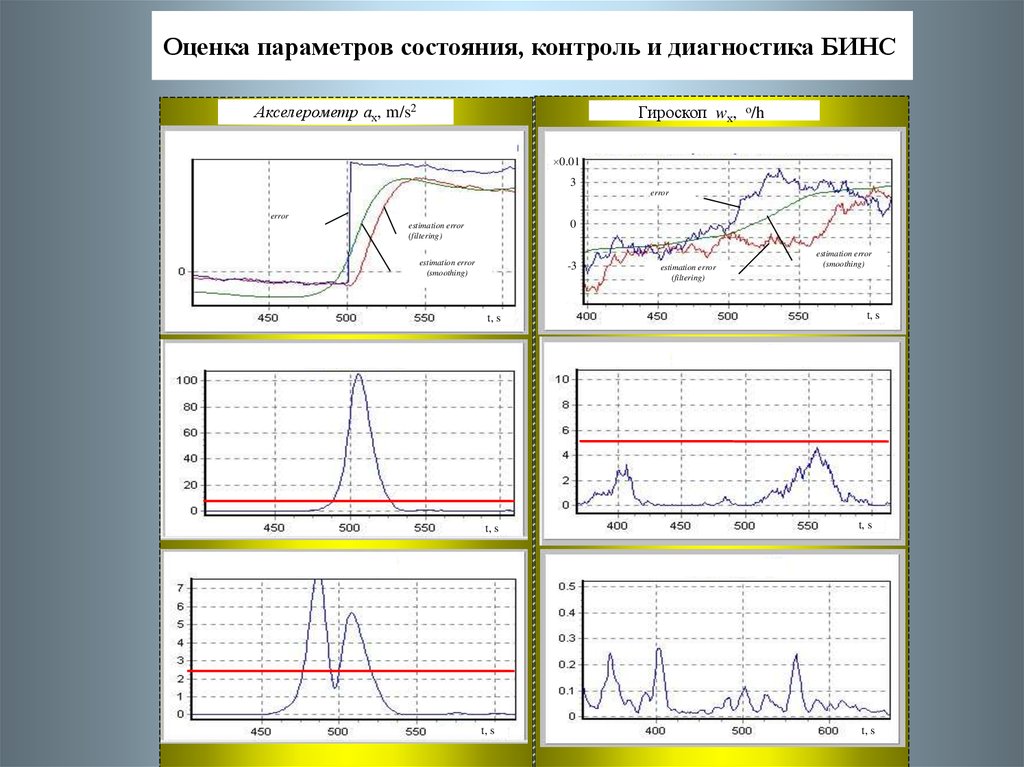
Оценка параметров состояния, контроль и диагностика БИНС
Акселерометр ах, m/s2
Гироскоп wх, o/h
0.01
3
error
error
0
estimation error
(filtering)
estimation error
(smoothing)
-3
t, s
t, s
t, s
estimation error
(filtering)
estimation error
(smoothing)
t, s
t, s
t, s

19.

При послеполетном диагностировании отказавший акселерометр
локализуется при превышении допусков обобщенными параметрами
FSaj
(критерий 2
)
и
(критерий 2 )
J Saj
(см. рис. 7.2), которые формируются по невязке ~
Sj . Можно также
видеть (см. рисунок 7.3), что отказ акселерометра несущественно
повлиял на изменение диагностических параметров J S j и FS j ,
характеризующих состояние гироскопа x .
Таким образом, комбинированная обработка наблюдений в
«прямом» и «обратном» времени позволяет решать задачи контроля и
диагностирования с глубиной до элемента вектора ошибок
динамической системы, какой является, например, ИНС.

20.

Методика выполнения КДЗ-3

21.

Дано: оценка вектора состояния ОК, полученная соответственно в
процессе фильтрации и сглаживания наблюдений, равны
x1 5 ;
2
x2 i / i
x1
3 ;
1
x2
i / N
Выполнить: контроль и диагностирование объекта по критерию
2 , если ковариационная матрица ошибок формирования
диагностического параметра имеет вид
1
0
1
0
1
3
1
P
i
/
i
3
1
0
2
0
1

22.

Методика решения
1.
ˆ
ˆ
x
x
i/N
(
i/i
1
)
N
i/i
2.
1
~
U
i/N
i
i/N
3.
4.
5.
~
~
T
1
J
D
s
(
i
)
i
i/N
i/N
?
2
JS(i) n
2
~
i
/
N
(
k
) 2
J
J
k
3
2
k
s
(
i
/
k
) s
(
i
/
k
1
)
k
D
i
(
kk
)