Похожие презентации:
Приведение квадратичной формы к главным осям
1.
33.6. Приведение квадратичной формы к главным осямЛюбая квадратичная форма ( x1 , ..., xn ) x A x
приводится к каноническому виду 1z12 ... n zn2
ортогональным преобразованием неизвестных
x Q z , Q ортогональная матрица, столбцами
которой служат компоненты собственных векторов
соответствующего симметрического преобразования;
0
1
T
матрица квадратичной
Q
A
Q
,
A
формы .
n
0
Всякая симметрическая матрица диагонализируема.
1
2.
Пример2
x1
2
x2
2
2 x3
2 x1 x2 4 x1 x3 4 x2 x3
3.
Пример2
x1
1 1 2
A 1 1 2
2 2 2
2
x2
2
2 x3
2 x1 x2 4 x1 x3 4 x2 x3
4.
Пример2
x1
1 1 2
A 1 1 2
2 2 2
2
x2
2
2 x3
2 x1 x2 4 x1 x3 4 x2 x3
λ – собственное значение А
| A E | 0
5.
Пример2
x1
1 1 2
A 1 1 2
2 2 2
1
2
x2
2
2 x3
λ – собственное значение А
| A E | 0
1
| A E | 1 1
2
2 x1 x2 4 x1 x3 4 x2 x3
2
2
2
2
2
( 2) ( 4)
λ1 λ 2 λ3 0
6.
Пример2
x1
1 1 2
A 1 1 2
2 2 2
1
2
x2
2
2 x3
λ – собственное значение А
| A E | 0
1
| A E | 1 1
2
2 x1 x2 4 x1 x3 4 x2 x3
2
2
2
2
2
( 2) ( 4)
λ1 λ 2 λ3 0
Собственные значения матрицы А: λ1,2 2, λ3 4 ;
Канонический вид квадратичной формы: 2 z 1 2 z2 4 z3
2
2
2
7.
Пример2
x1
1 1 2
A 1 1 2
2 2 2
1
2
x2
2
2 x3
λ – собственное значение А
| A E | 0
1
| A E | 1 1
2
2 x1 x2 4 x1 x3 4 x2 x3
2
2
2
2
( 2) ( 4)
2
λ1 λ 2 λ3 0
Собственные значения матрицы А: λ1,2 2, λ3 4 ;
Канонический вид квадратичной формы: 2 z 1 2 z2 4 z3
2
Для отыскания собственных векторов
решаем ОСЛУ (*0) : ( A E ) x 0
2
2
8.
С.з. 1, 2 2 :1 1 2
A 2 , 3 E 1 1 2
2 2 4
9.
С.з. 1, 2 2 :1 1 2 1 1 2
A 2 , 3 E 1 1 2 ~ 0 0 0
2 2 4 0 0 0
10.
С.з. 1, 2 2 :1 1 2 1 1 2
A 2 , 3 E 1 1 2 ~ 0 0 0
0 0 0
2 2 4
1
2
v1 1 , v 2 0 – ФСР ОСЛУ (*0) : x1 x2 2 x3 0 ;
0
1
( x2, x3 свободные неизвестные)
11.
С.з. 1, 2 2 :1 1 2 1 1 2
A 2 , 3 E 1 1 2 ~ 0 0 0
2 2 4 0 0 0
1
2
v1 1 , v 2 0 – ФСР ОСЛУ (*0) : x1 x2 2 x3 0 ;
0
1
( x2, x3 свободные неизвестные)
Общий вид собственного вектора матрицы А при
собственном значении 1, 2 2 : s v1 t v 2 , где s 0 ,
t 0 ;
12.
С.з. 1, 2 2 :1 1 2 1 1 2
A 2 , 3 E 1 1 2 ~ 0 0 0
2 2 4 0 0 0
1
2
v1 1 , v 2 0 – ФСР ОСЛУ (*0) : x1 x2 2 x3 0 ;
0
1
( x2, x3 свободные неизвестные)
Общий вид собственного вектора матрицы А при
собственном значении 1, 2 2 : s v1 t v 2 , где s 0 ,
t 0 ;
Выбранные векторы неортогональны, а нам нужен
ортонормированный базис из собственных векторов А.
13.
Можно применить процесс ортогонализации:2
1 1
1
(v2, f1)
f1 1 , f2 v2
f1 0 2 1 1
0
1 2 0 1
( f1, f1)
14.
Можно применить процесс ортогонализации:2
1 1
1
(v2, f1)
f1 1 , f2 v2
f1 0 2 1 1
0
1 2 0 1
( f1, f1)
15.
Можно применить процесс ортогонализации:2
1 1
1
(v2, f1)
f1 1 , f2 v2
f1 0 2 1 1
0
1 2 0 1
( f1, f1)
Нормируя эти векторы, получим первые два вектора
искомого ортонормированного базиса:
1
1
1
1
1
1
h1
f1
1 , h2
f 1
2 0
3 1
| f1 |
| f2 |
16.
Можно применить процесс ортогонализации:2
1 1
1
(v2, f1)
f1 1 , f2 v2
f1 0 2 1 1
0
1 2 0 1
( f1, f1)
Нормируя эти векторы, получим первые два вектора
искомого ортонормированного базиса:
1
1
1
1
1
1
h1
f1
1 , h2
f 1
2 0
3 1
| f1 |
| f2 |
Третий вектор искомого базиса можно угадать ‒
он должен быть ортогонален найденным.
17.
Можно применить процесс ортогонализации:2
1 1
1
(v2, f1)
f1 1 , f2 v2
f1 0 2 1 1
0
1 2 0 1
( f1, f1)
Нормируя эти векторы, получим первые два вектора
искомого ортонормированного базиса:
1
1
1
1
1
1
h1
f1
1 , h2
f 1
2 0
3 1
| f1 |
| f2 |
Третий вектор искомого базиса можно угадать ‒
он должен быть ортогонален найденным.
Собственные векторы симметрической матрицы, соответствующие
различным собственным значениям, попарно ортогональны.
18.
5 1 2 1 5 2С.з. 3 4 : A 3 E 1 5 2 ~ 5 1 2 ~
2 2 2 2 2 2
19.
5 1 2 1 5 2С.з. 3 4 : A 3 E 1 5 2 ~ 5 1 2 ~
2 2 2 2 2 2
1 5 2
~ 0 24 12
0 12 6
20.
5 1 2С.з. 3 4 : A 3 E 1 5 2 ~
2 2 2
1 5 2 1 5 2 1 1
~ 0 24 12 ~ 0 2 1 ~ 0 2
0 12 6 0 0 0
0 0
1 5 2
5 1 2 ~
2 2 2
0
1 .
0
21.
5 1 2 1 5 2С.з. 3 4 : A 3 E 1 5 2 ~ 5 1 2 ~
2 2 2 2 2 2
1 5 2 1 5 2 1 1 0
~ 0 24 12 ~ 0 2 1 ~ 0 2 1 .
0 12 6 0 0 0
0
0
0
1
x1 x2 0 ,
Вектор u 1 – ФСР ОСЛУ (*0) :
2 x2 x3 0
2
(при свободном неизвестном x 1) .
2
22.
5 1 2 1 5 2С.з. 3 4 : A 3 E 1 5 2 ~ 5 1 2 ~
2 2 2 2 2 2
1 5 2 1 5 2 1 1 0
~ 0 24 12 ~ 0 2 1 ~ 0 2 1 .
0 12 6 0 0 0
0
0
0
1
x1 x2 0 ,
Вектор u 1 – ФСР ОСЛУ (*0) :
2 x2 x3 0
2
(при свободном неизвестном x 1) .
2
1/ 6
‒ единичный собственный
1
h3
u 1/ 6
|u |
2 / 6 вектор матрицы А при
собственном значении 4 .
3
23.
Столбцами искомой ортогональной матрицы переходаQ (матрицы замены переменных) служат найденные
единичные собственные векторы матрицы А:
24.
Столбцами искомой ортогональной матрицы переходаQ (матрицы замены переменных) служат найденные
единичные собственные векторы матрицы А:
1/ 2 1/ 3 1/ 6
Q 1/ 2 1/ 3 1/ 6
0
1
/
3
2
/
6
25.
Столбцами искомой ортогональной матрицы переходаQ (матрицы замены переменных) служат найденные
единичные собственные векторы матрицы А:
Ответ:
2
2 z1
2
2 z2
2
4 z3
x1 1 / 2 1 / 3 1 / 6 z 1
x2 1 / 2 1 / 3 1 / 6 z2
x 0
1 / 3 2 / 6 z3
3
26.
Столбцами искомой ортогональной матрицы переходаQ (матрицы замены переменных) служат найденные
единичные собственные векторы матрицы А:
Ответ:
2
2 z1
2
2 z2
2
4 z3
x1 1 / 2 1 / 3 1 / 6 z 1
x2 1 / 2 1 / 3 1 / 6 z2
x 0
1 / 3 2 / 6 z3
3
Знаки единичных векторов h 1 u обычно выбирают
|u |
так, чтобы det Q 1.
27.
34. Кривые второго порядка27
28.
34. Кривые второго порядка34.1. Общее уравнение
O, i , j – прямоугольная
декартова
система координат
28
29.
34. Кривые второго порядка34.1. Общее уравнение
O, i , j – прямоугольная
декартова
система координат
Кривой второго порядка называется множество
точек плоскости, задаваемое уравнением
a11x a22 y 2a12 xy 2b1x 2b 2 y c 0.
2
2
29
30.
34. Кривые второго порядка34.1. Общее уравнение
O, i , j – прямоугольная
декартова
система координат
Кривой второго порядка называется множество
точек плоскости, задаваемое уравнением
a11x a22 y 2a12 xy 2b1x 2b 2 y c 0.
~
x
x
34.2. Заменой переменных Q уравнение
~
y
y
2
2
можно упростить, приведя квадратичную форму
a11x 2 2a12 xy a22 y 2 к главным осям (п. 33.6):
30
31.
1~x 2 2 ~
y 2,
31
32.
1~x 2 2 ~
y 2,
~ ~
выбирая на плоскости новый базис i , j :
~
~
~ ~
| i | | j | 1; i j
32
33.
1~x 2 2 ~
y 2,
~ ~
выбирая на плоскости новый базис i , j :
~
~
~
~
~
i q11 i q21 j
| i | | j | 1; i j
~
j q12 i q22 j
33
34.
1~x 2 2 ~
y 2,
~ ~
выбирая на плоскости новый базис i , j :
~
~
~
~
~
i q11 i q21 j
| i | | j | 1; i j
~
j q12 i q22 j
q11 q12
-- собственные векторы матрицы
q21 q22
a11 a12 квадратичной
A
a21 a22 формы φ,
соответствующие собственным значениям λ1 и λ2.
34
35.
34.3. Выбирая, если нужно, новое начало координат,~
~
x0
x
x
ˆ
~
~
ˆ
O ( x0; y0 ) − заменой переменных
~
~
y
y
ˆ
y0
35
36.
34.3. Выбирая, если нужно, новое начало координат,~
~
x0
x
x
ˆ
~
~
ˆ
O ( x0; y0 ) − заменой переменных
~
~
y
y
ˆ
y0
уравнение кривой приводят к каноническому виду
− одному из девяти:
36
37.
34.3. Выбирая, если нужно, новое начало координат,~
~
x0
x
x
ˆ
~
~
ˆ
O ( x0; y0 ) − заменой переменных
~
~
y
y
ˆ
y0
уравнение кривой приводят к каноническому виду
− одному из девяти:
1)
2)
xˆ 2 yˆ 2
− эллипс
1
a 2 b2
(a b 0)
37
38.
34.3. Выбирая, если нужно, новое начало координат,~
~
x0
x
x
ˆ
~
~
ˆ
O ( x0; y0 ) − заменой переменных
~
~
y
y
ˆ
y0
уравнение кривой приводят к каноническому виду
− одному из девяти:
1)
2)
xˆ 2 yˆ 2
− эллипс
1
a 2 b2
(a b 0)
действительный (+)
мнимый (−) ;
38
39.
34.3. Выбирая, если нужно, новое начало координат,~
~
x0
x
x
ˆ
~
~
ˆ
O ( x0; y0 ) − заменой переменных
~
~
y
y
ˆ
y0
уравнение кривой приводят к каноническому виду
− одному из девяти:
1)
2)
xˆ 2 yˆ 2
− эллипс
1
a 2 b2
(a b 0)
действительный (+)
мнимый (−) ;
yˆ 2
3)
2 1 − гипербола (a, b 0) ;
2
a
b
xˆ 2
39
40.
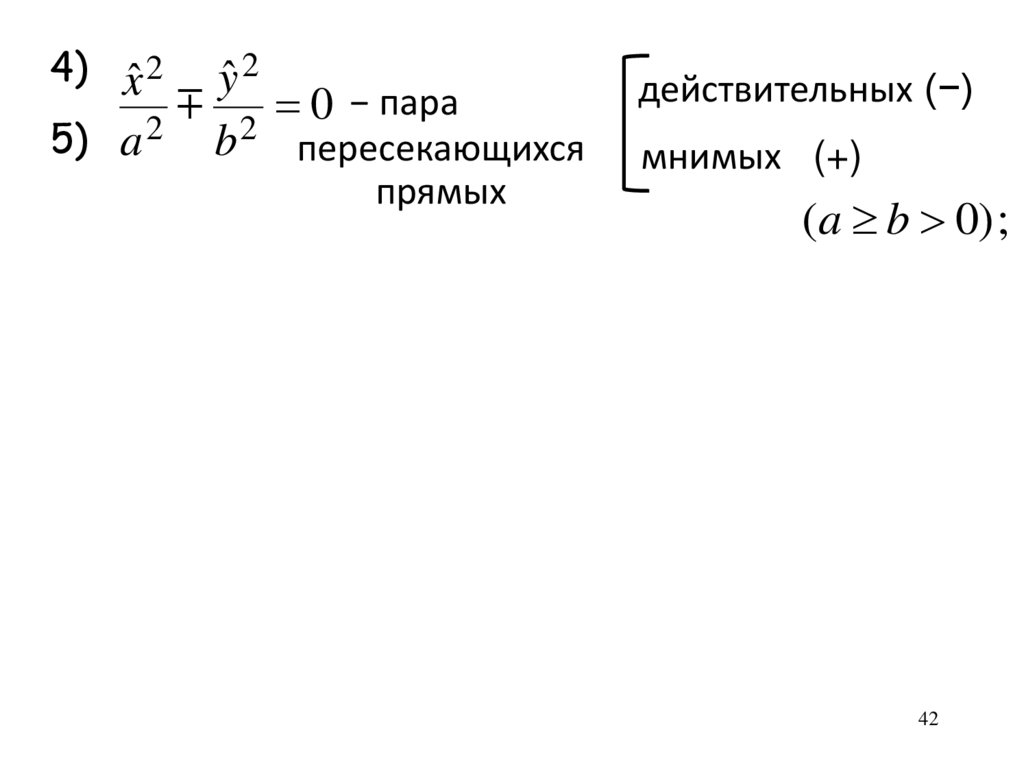
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
1−5
действительных (−)
мнимых (+)
(a b 0) ;
− уравнения центральных кривых второго порядка.
6) yˆ 2 2 p xˆ − парабола (p > 0);
7) 2
yˆ a 2 − пара
8)
параллельных
прямых
9)
действительных (+)
мнимых (−) (a 0) ;
yˆ 2 0 − пара совпавших прямых.
40
41.
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
41
42.
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
действительных (−)
мнимых (+)
(a b 0) ;
42
43.
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
1−5
действительных (−)
мнимых (+)
(a b 0) ;
− уравнения центральных кривых второго порядка.
43
44.
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
1−5
действительных (−)
мнимых (+)
(a b 0) ;
− уравнения центральных кривых второго порядка.
6) yˆ 2 2 p xˆ − парабола (p > 0);
44
45.
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
1−5
действительных (−)
мнимых (+)
(a b 0) ;
− уравнения центральных кривых второго порядка.
6) yˆ 2 2 p xˆ − парабола (p > 0);
7) 2
yˆ a 2 − пара
8)
параллельных
прямых
45
46.
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
1−5
действительных (−)
мнимых (+)
(a b 0) ;
− уравнения центральных кривых второго порядка.
6) yˆ 2 2 p xˆ − парабола (p > 0);
7) 2
yˆ a 2 − пара
8)
параллельных
прямых
действительных (+)
мнимых (−) (a 0) ;
46
47.
4) xˆ 2 yˆ 2− пара
0
5) a 2 b 2 пересекающихся
прямых
1−5
действительных (−)
мнимых (+)
(a b 0) ;
− уравнения центральных кривых второго порядка.
6) yˆ 2 2 p xˆ − парабола (p > 0);
7) 2
yˆ a 2 − пара
8)
параллельных
прямых
9)
действительных (+)
мнимых (−) (a 0) ;
yˆ 2 0 − пара совпавших прямых.
47
48.
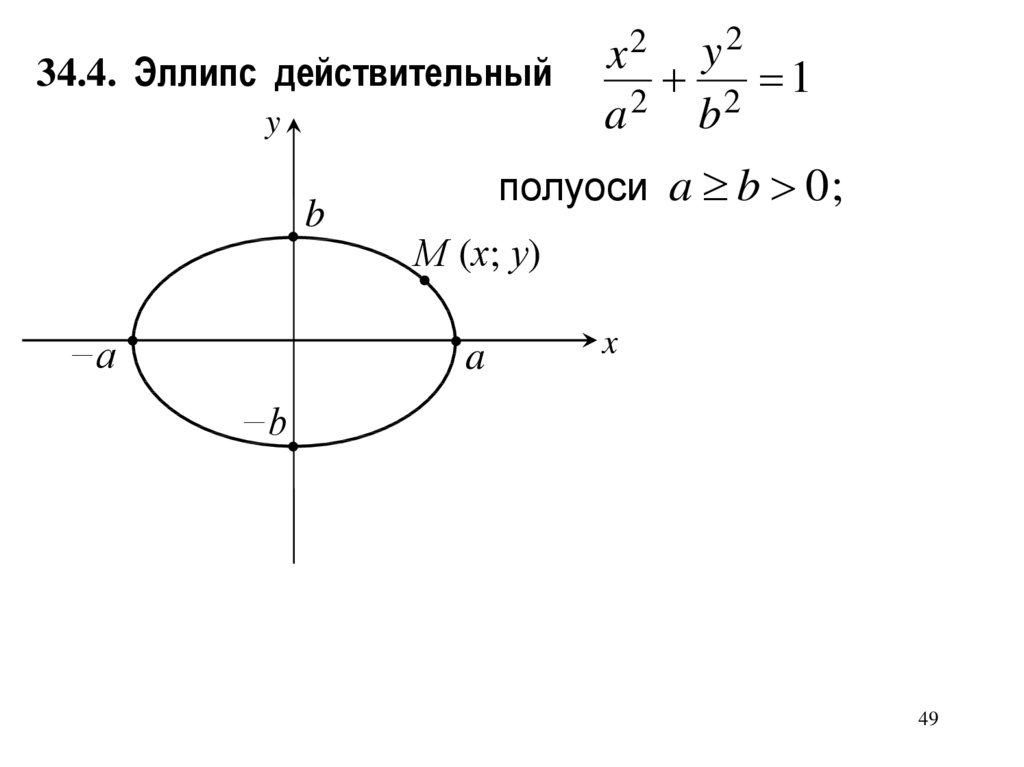
34.4. Эллипс действительныйy2
2 1
2
a
b
x2
48
49.
34.4. Эллипс действительныйy
b
−a
y2
2 1
2
a
b
x2
полуоси a b 0 ;
М (х; у)
a
x
−b
49
50.
34.4. Эллипс действительныйy
b
−a
полуоси a b 0 ;
М (х; у)
a
−b
y2
2 1
2
a
b
x2
(при a = b − окружность
радиуса a);
x
c a 2 b2 ;
50
51.
34.4. Эллипс действительныйy
полуоси a b 0 ;
b
−a
F1
М (х; у)
F2
−b
y2
2 1
2
a
b
x2
a
(при a = b − окружность
радиуса a);
x
c a 2 b2 ;
F1,2 ( c; 0) фокусы;
51
52.
34.4. Эллипс действительныйy
полуоси a b 0 ;
b
−a
F1
М (х; у)
F2
−b
y2
2 1
2
a
b
x2
a
(при a = b − окружность
радиуса a);
x
c a 2 b2 ;
F1,2 ( c; 0) фокусы;
M Э | MF1 | | MF2 | 2a
52
53.
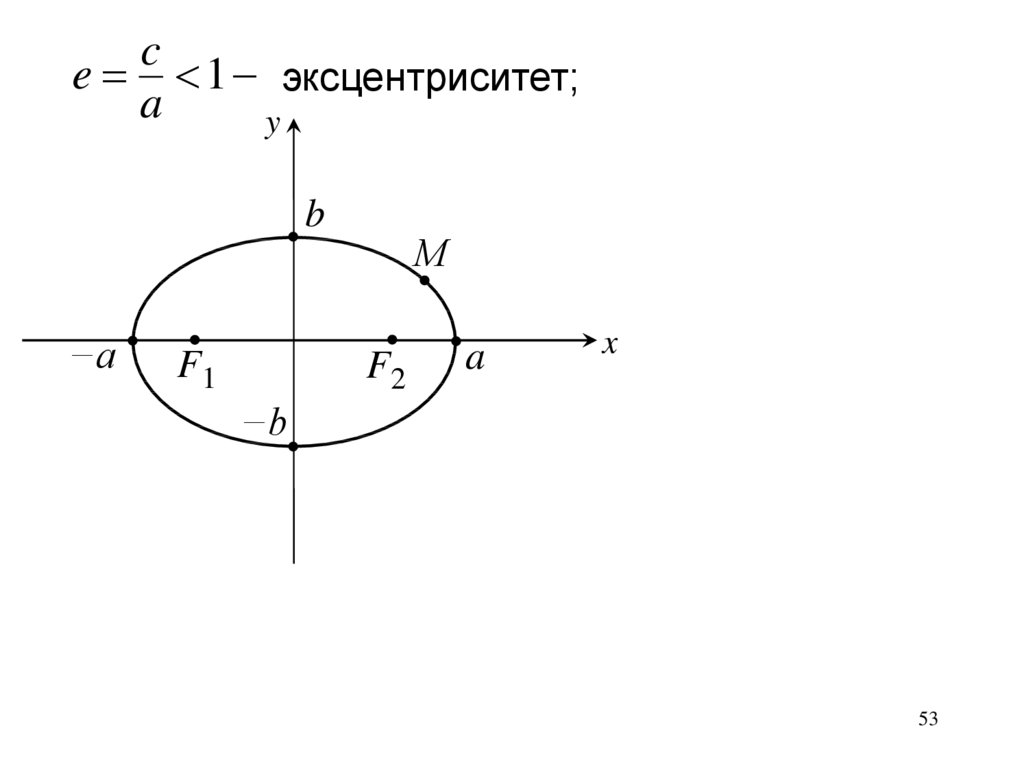
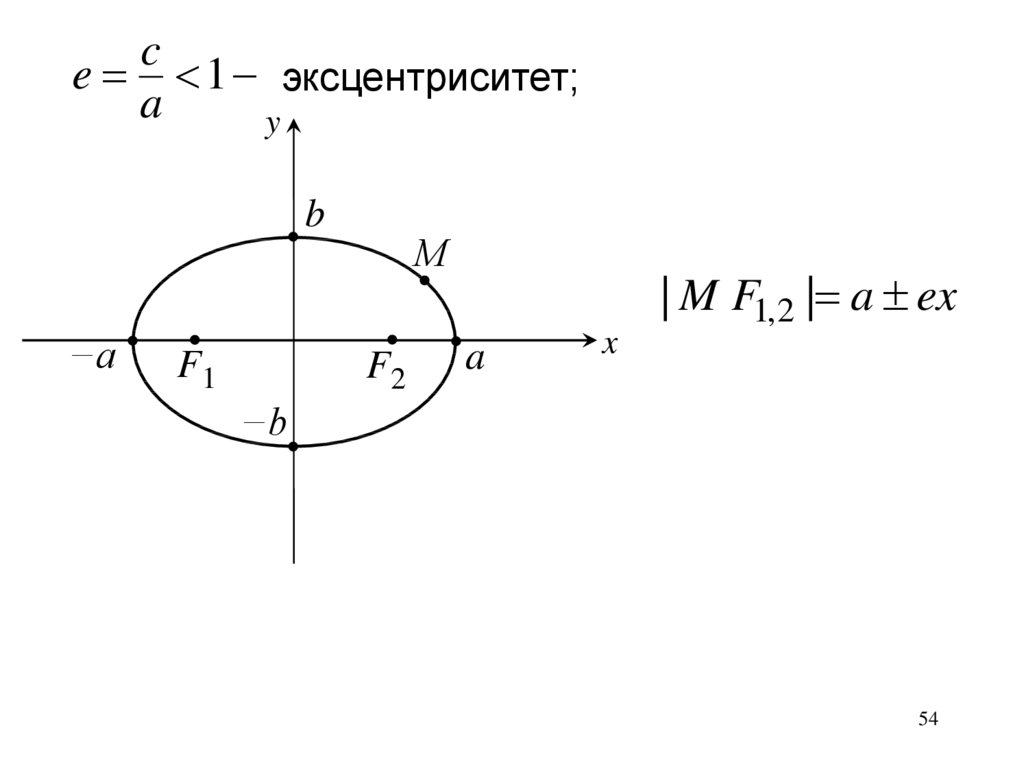
ce 1 эксцентриситет;
a
y
b
−a
F1
М
F2
a
x
−b
53
54.
ce 1 эксцентриситет;
a
y
b
−a
F1
М
F2
| M F1,2 | a ex
a
x
−b
54
55.
ce 1 эксцентриситет;
a
y
a
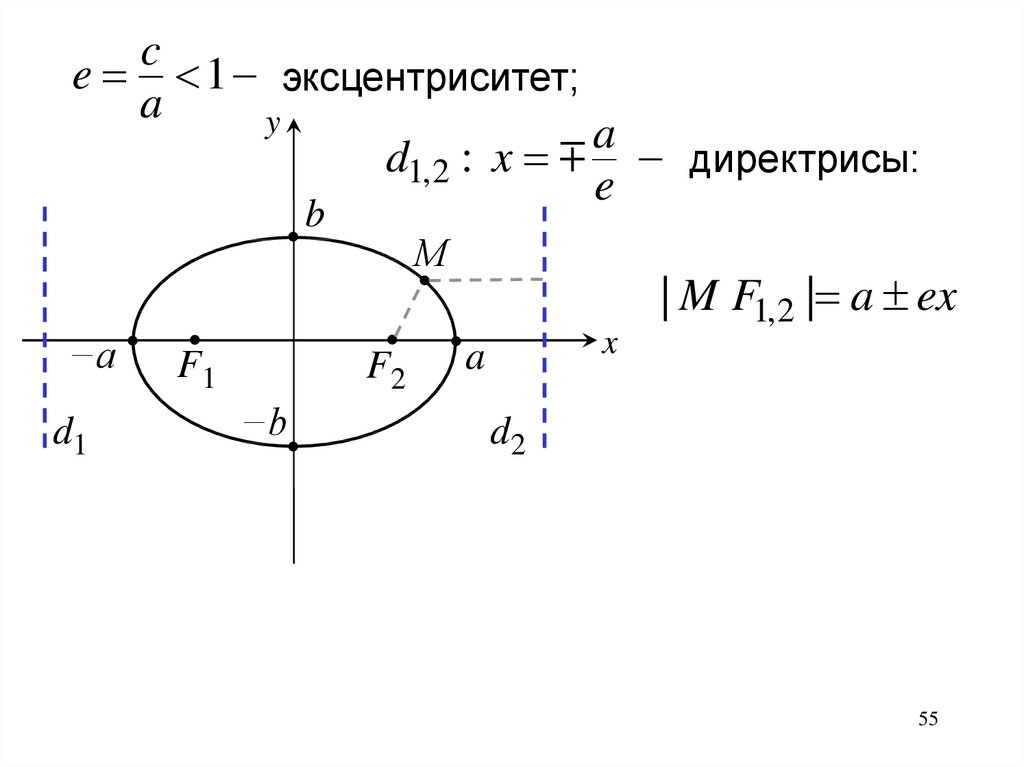
d1, 2 : x директрисы:
e
b
−a
d1
F1
М
F2
−b
| M F1,2 | a ex
x
a
d2
55
56.
ce 1 эксцентриситет;
a
y
a
d1, 2 : x директрисы:
e
b
−a
d1
F1
М
F2
−b
| M F1,2 | a ex
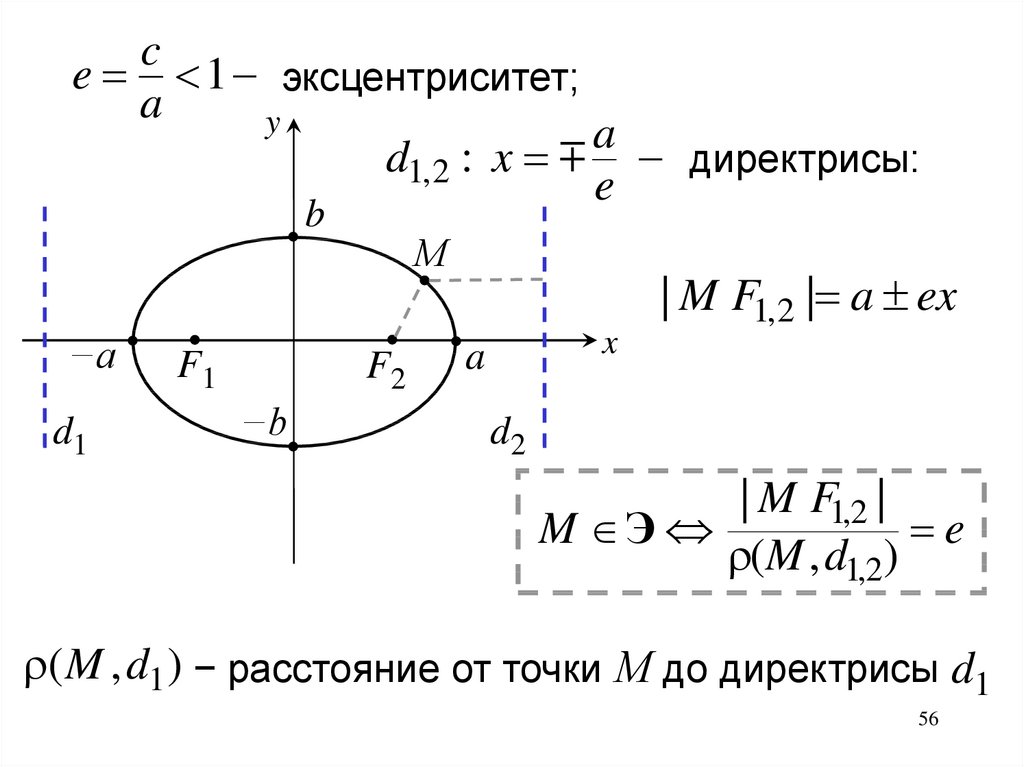
x
a
d2
| M F1,2 |
M Э
e
(M , d1,2)
( M , d1 ) − расстояние от точки М до директрисы d1
56
57.
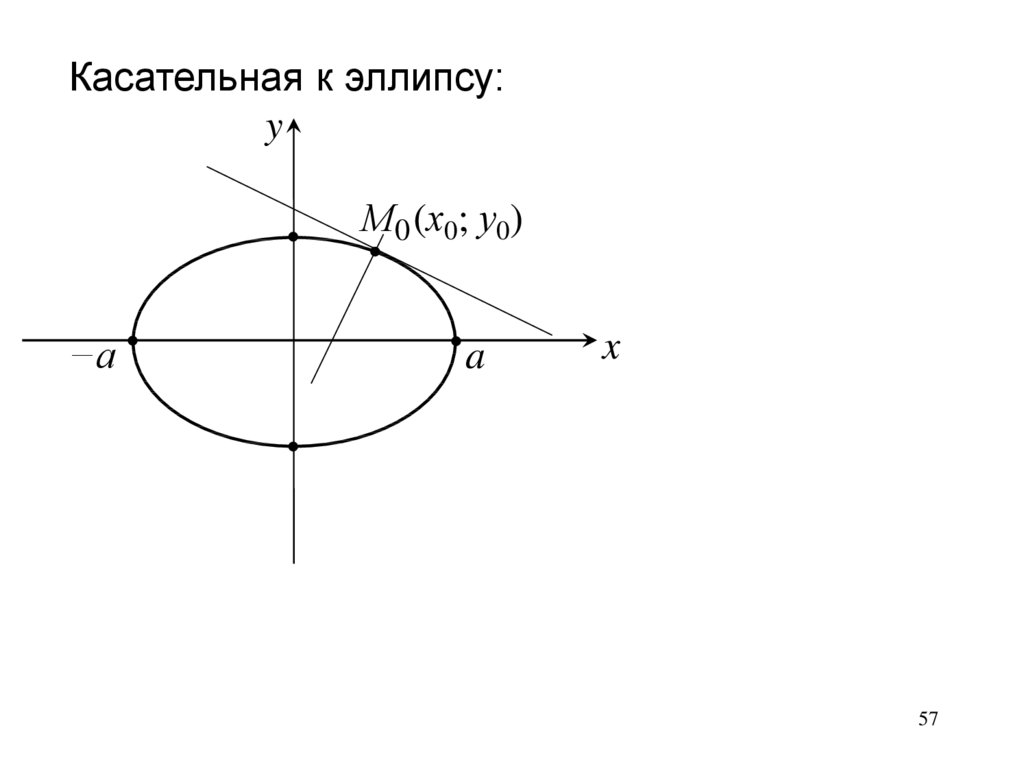
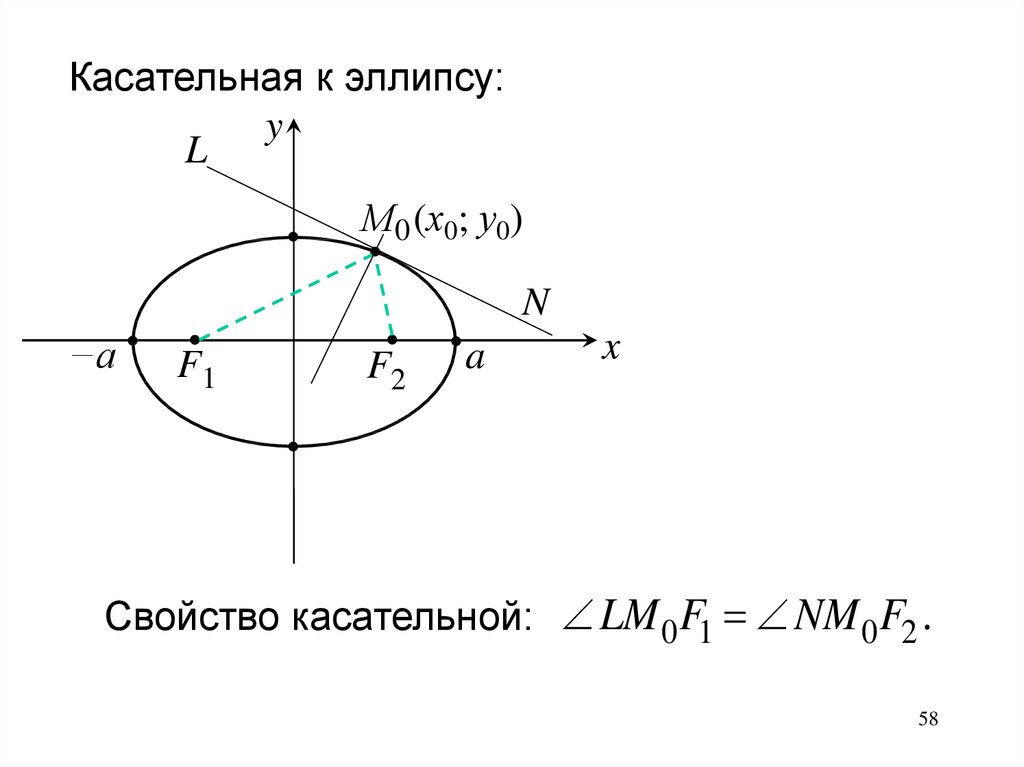
Касательная к эллипсу:y
М0 (х0; у0)
−a
a
x
57
58.
Касательная к эллипсу:y
L
М0 (х0; у0)
N
−a
F1
F2
a
x
Свойство касательной: LM 0 F1 NM 0 F2 .
58
59.
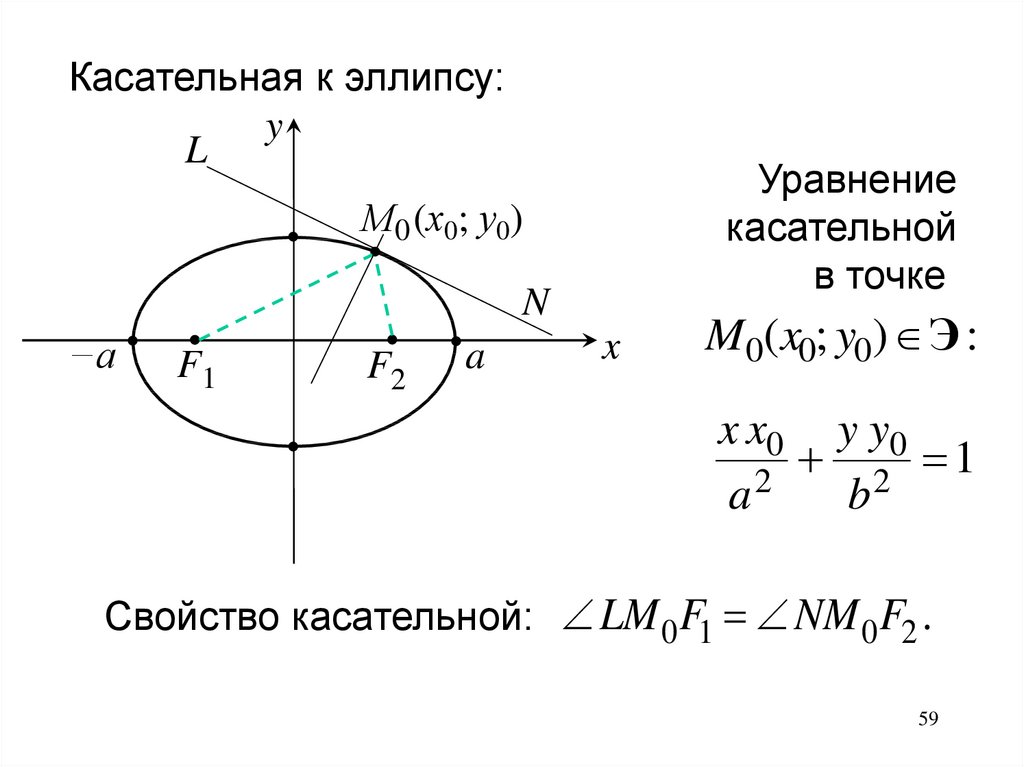
Касательная к эллипсу:y
L
Уравнение
касательной
в точке
М0 (х0; у0)
N
−a
F1
F2
a
x
M0(x0; y0) Э :
x x0 y y0
2 1
2
a
b
Свойство касательной: LM 0 F1 NM 0 F2 .
59
60.
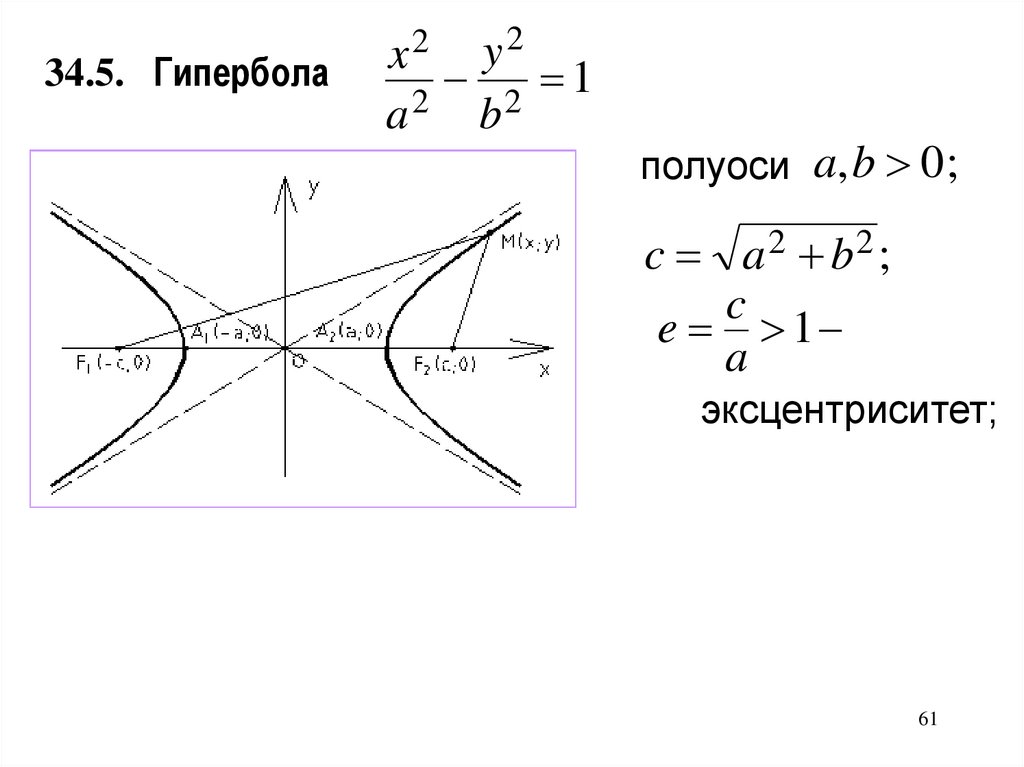
34.5. Гиперболаy2
2 1
2
a
b
x2
полуоси a, b 0 ;
60
61.
34.5. Гиперболаy2
2 1
2
a
b
x2
полуоси a, b 0 ;
c a 2 b2 ;
c
e 1
a
эксцентриситет;
61
62.
34.5. Гиперболаy2
2 1
2
a
b
x2
полуоси a, b 0 ;
c a 2 b2 ;
c
e 1
a
эксцентриситет;
b
y x асимптоты;
a
62
63.
y22 1
2
a
b
x2
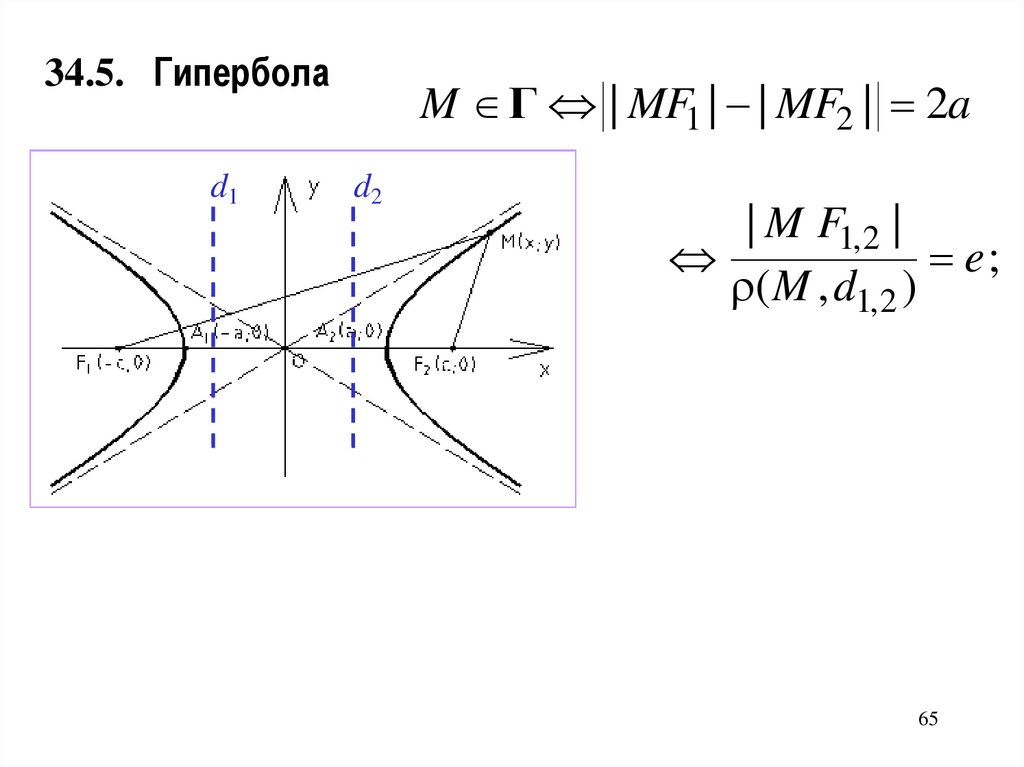
34.5. Гипербола
d1
d2
полуоси a, b 0 ;
c a 2 b2 ;
c
e 1
a
эксцентриситет;
b
y x асимптоты;
a
F1,2 ( c; 0) фокусы;
a
d1, 2 : x директрисы:
e
63
64.
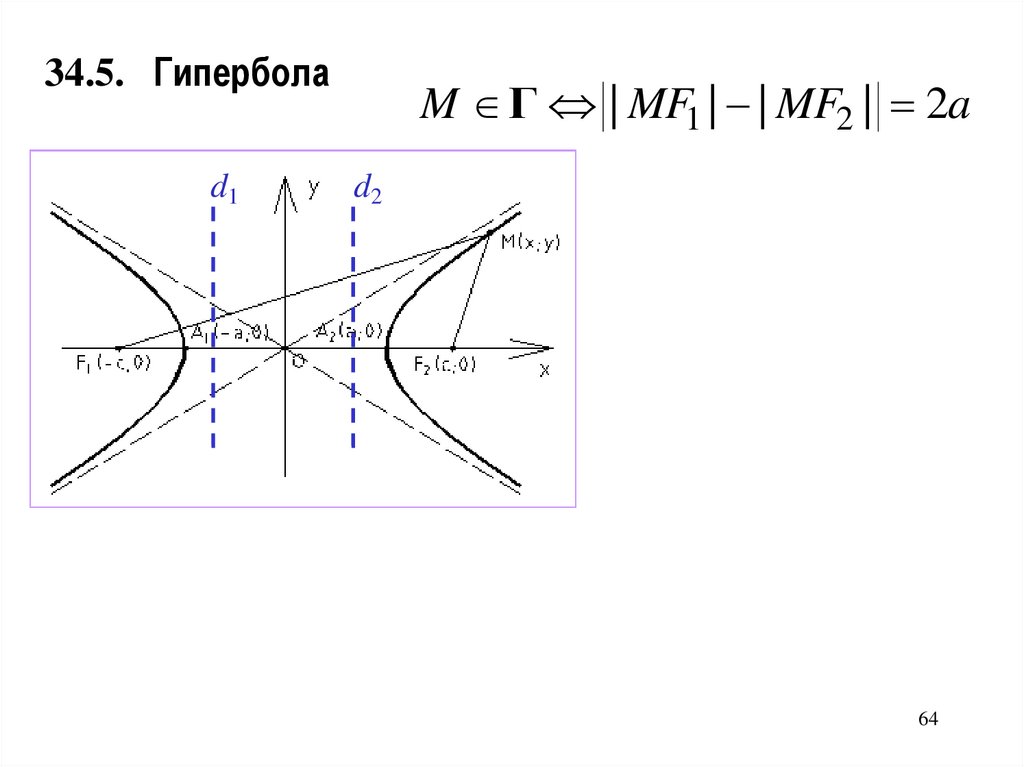
34.5. Гиперболаd1
M Г | MF1 | | MF2 | 2a
d2
64
65.
34.5. Гиперболаd1
M Г | MF1 | | MF2 | 2a
d2
| M F1, 2 |
e;
( M , d1, 2 )
65
66.
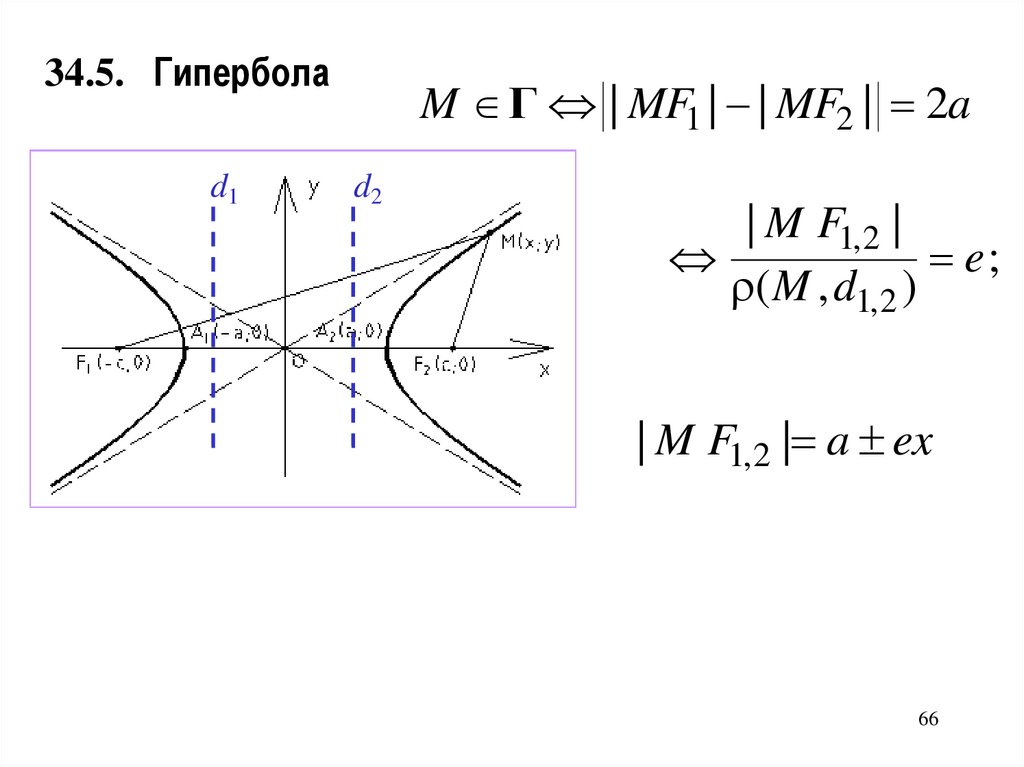
34.5. Гиперболаd1
M Г | MF1 | | MF2 | 2a
d2
| M F1, 2 |
e;
( M , d1, 2 )
| M F1,2 | a ex
66
67.
34.5. Гиперболаd1
M Г | MF1 | | MF2 | 2a
d2
| M F1, 2 |
e;
( M , d1, 2 )
| M F1,2 | a ex
Уравнение касательной
в точке M 0 ( x0 ; y0 ) Г :
x x0 y y0
1
a2
b2
67
68.
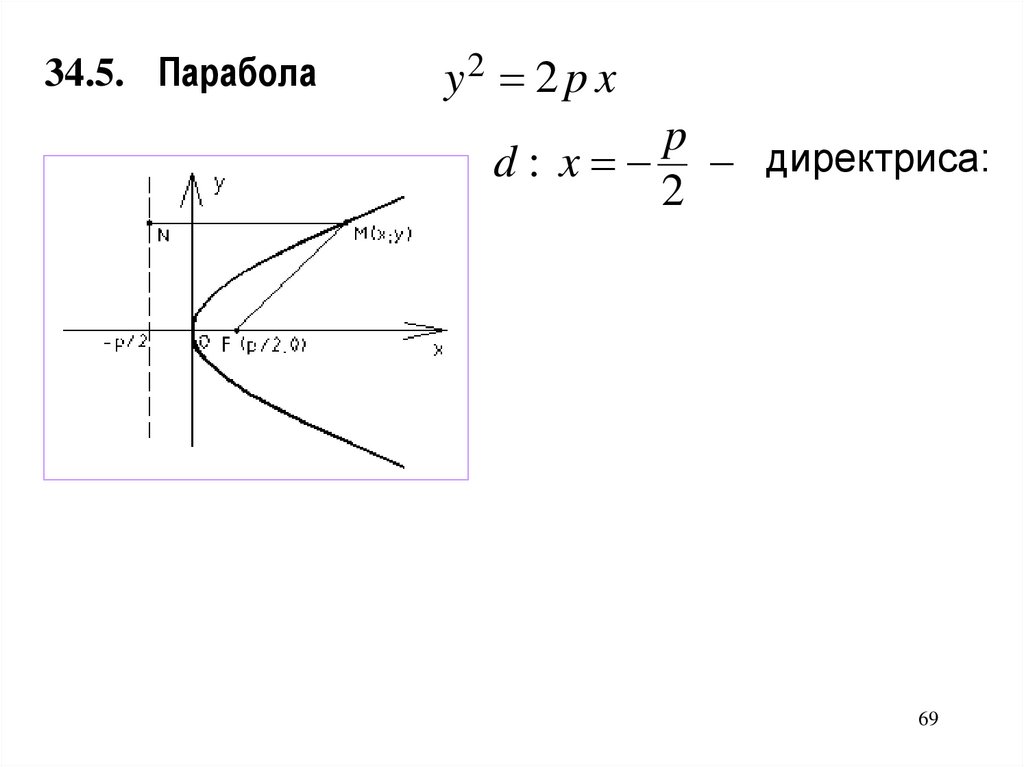
34.5. Параболаy2 2 p x
68
69.
34.5. Параболаy2 2 p x
p
d : x директриса:
2
69
70.
34.5. Параболаy2 2 p x
p
d : x директриса:
2
p
F ; 0 фокус;
2
M П | F M | ( M , d )
70
71.
34.5. Параболаy2 2 p x
p
d : x директриса:
2
p
F ; 0 фокус;
2
M П | F M | ( M , d )
Уравнение касательной
в точке M 0(x0; y0) П :
y y0 p x p x0
71
72.
~ ~ˆ
34.6. Система координат O, i , j , в которой
уравнение кривой второго порядка имеет
канонический вид, называется канонической.
72
73.
~ ~ˆ
34.6. Система координат O, i , j , в которой
уравнение кривой второго порядка имеет
канонический вид, называется канонической.
Каноническая система координат определяется,
вообще говоря, неоднозначно.
73
74.
35. Поверхности второго порядка74
75.
35. Поверхности второго порядка35.1. Общее уравнение
O, i , j, k – п.д.с.к.
75
76.
35. Поверхности второго порядка35.1. Общее уравнение
O, i , j, k – п.д.с.к.
Поверхностью второго порядка называется
множество точек пространства, задаваемое уравнением
a11x 2 a22 y 2 a33 z 2 2a12 xy 2a13 xz 2a23 yz
2b1x 2b2 y 2b3 z c 0
76
77.
35. Поверхности второго порядка35.1. Общее уравнение
O, i , j, k – п.д.с.к.
Поверхностью второго порядка называется
множество точек пространства, задаваемое уравнением
a11x 2 a22 y 2 a33 z 2 2a12 xy 2a13 xz 2a23 yz
2b1x 2b2 y 2b3 z c 0
~
x
x
y Q ~
35.2. Заменой переменных
y (п. 33.6)
~
(Q ‒ ортогональная матрица) z
z
77
78.
35. Поверхности второго порядка35.1. Общее уравнение
O, i , j, k – п.д.с.к.
Поверхностью второго порядка называется
множество точек пространства, задаваемое уравнением
a11x 2 a22 y 2 a33 z 2 2a12 xy 2a13 xz 2a23 yz
2b1x 2b2 y 2b3 z c 0
~
x
x
y Q ~
35.2. Заменой переменных
y (п. 33.6)
~
(Q ‒ ортогональная матрица) z
z
уравнение можно упростить,
приведя квадратичную форму
78
79.
~~
~
2
2
2,
x
y
z
к главным осям,
1
2
3
~ ~ ~
выбирая в пространстве новый базис i , j , k :
~ ~ ~
~ ~ ~ ~
| i | | j | | k | 1; i j k i .
35.3. Выбирая, если нужно, новое начало координат,
Oˆ ( ~
x0 ; ~
y0 ; ~
z0 )
~
~
ˆ
x
x
x0
− заменой
~
y yˆ ~
y0
переменных ~ ~
z zˆ z0
уравнение поверхности приводят к
каноническому виду − одному из семнадцати:
79
80.
~~
~
2
2
2,
x
y
z
к главным осям,
1
2
3
80
81.
~~
~
2
2
2,
x
y
z
к главным осям,
1
2
3
~ ~ ~
выбирая в пространстве новый базис i , j , k :
~ ~ ~
~ ~ ~ ~
| i | | j | | k | 1; i j k i .
81
82.
~~
~
2
2
2,
x
y
z
к главным осям,
1
2
3
~ ~ ~
выбирая в пространстве новый базис i , j , k :
~ ~ ~
~ ~ ~ ~
| i | | j | | k | 1; i j k i .
35.3. Выбирая, если нужно, новое начало координат,
Oˆ ( ~
x0 ; ~
y0 ; ~
z0 )
82
83.
~~
~
2
2
2,
x
y
z
к главным осям,
1
2
3
~ ~ ~
выбирая в пространстве новый базис i , j , k :
~ ~ ~
~ ~ ~ ~
| i | | j | | k | 1; i j k i .
35.3. Выбирая, если нужно, новое начало координат,
Oˆ ( ~
x0 ; ~
y0 ; ~
z0 )
~
~
ˆ
x
x
x0
− заменой
~
y yˆ ~
y0
переменных ~ ~
z zˆ z0
уравнение поверхности приводят к
каноническому виду
83
84.
~~
~
2
2
2,
x
y
z
к главным осям,
1
2
3
~ ~ ~
выбирая в пространстве новый базис i , j , k :
~ ~ ~
~ ~ ~ ~
| i | | j | | k | 1; i j k i .
35.3. Выбирая, если нужно, новое начало координат,
Oˆ ( ~
x0 ; ~
y0 ; ~
z0 )
~
~
ˆ
x
x
x0
− заменой
~
y yˆ ~
y0
переменных ~ ~
z zˆ z0
уравнение поверхности приводят к
каноническому виду − одному из семнадцати:
84
85.
1) xˆ2
2
a
2)
yˆ 2
b2
zˆ 2
c2
Эллипсоиды:
1
действительный (+)
(a b c 0) мнимый (−) ;
85
86.
1) xˆ2
2
a
2)
3) xˆ
2
2
a
4)
yˆ 2
b2
yˆ 2
b2
zˆ 2
c2
zˆ 2
Эллипсоиды:
1
действительный (+)
(a b c 0) мнимый (−) ;
Гиперболоиды:
1
c 2 (a b 0)
однополостный (+)
двуполостный (−);
86
87.
1) xˆ2
2
a
2)
3) xˆ
2
2
a
4)
5) xˆ 2
6) a
2
yˆ 2
b2
yˆ 2
b2
yˆ 2
b2
zˆ 2
c2
zˆ 2
Эллипсоиды:
1
(a b c 0) мнимый (−) ;
Гиперболоиды:
1
c 2 (a b 0)
zˆ 2
действительный (+)
однополостный (+)
двуполостный (−);
Конусы:
действительный (−) (a b 0),
0
c2
мнимый (+) (a b c 0);
87
88.
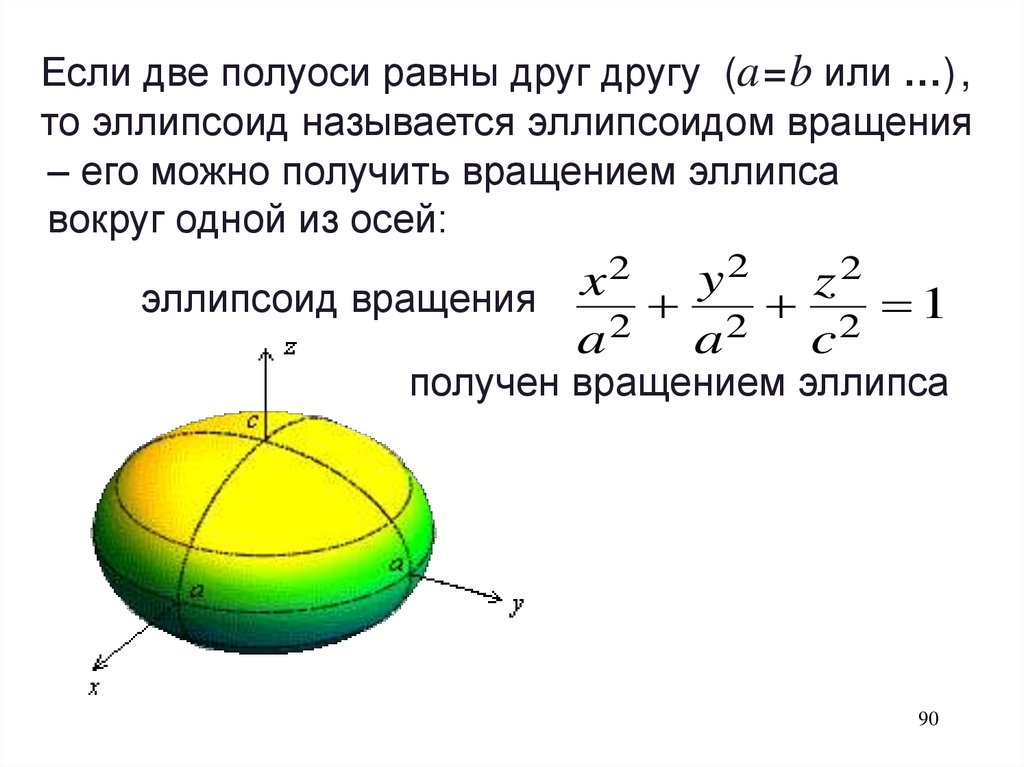
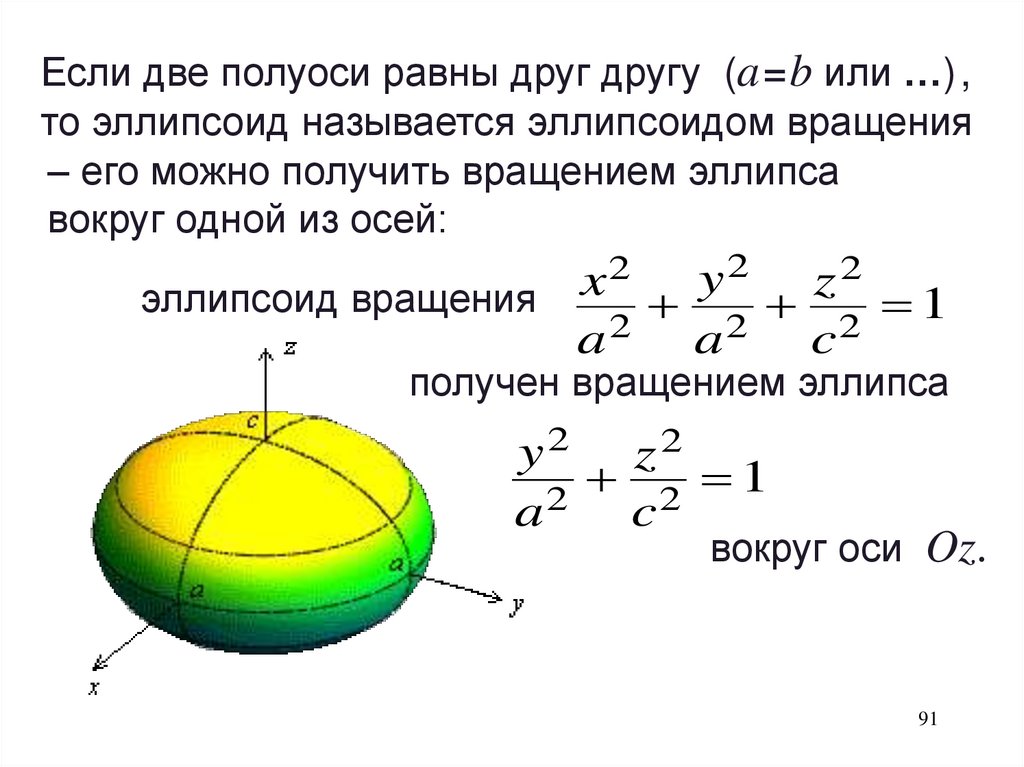
Если две полуоси равны друг другу (a = b или …) ,то эллипсоид называется эллипсоидом вращения
88
89.
Если две полуоси равны друг другу (a = b или …) ,то эллипсоид называется эллипсоидом вращения
‒ его можно получить вращением эллипса
вокруг одной из осей:
89
90.
Если две полуоси равны друг другу (a = b или …) ,то эллипсоид называется эллипсоидом вращения
‒ его можно получить вращением эллипса
вокруг одной из осей:
2
2
2
y
x
z
эллипсоид вращения
2 2 1
2
a
a
c
получен вращением эллипса
90
91.
Если две полуоси равны друг другу (a = b или …) ,то эллипсоид называется эллипсоидом вращения
‒ его можно получить вращением эллипса
вокруг одной из осей:
2
2
2
y
x
z
эллипсоид вращения
2 2 1
2
a
a
c
получен вращением эллипса
y2 z2
2 1
2
a
c
вокруг оси Oz.
91
92.
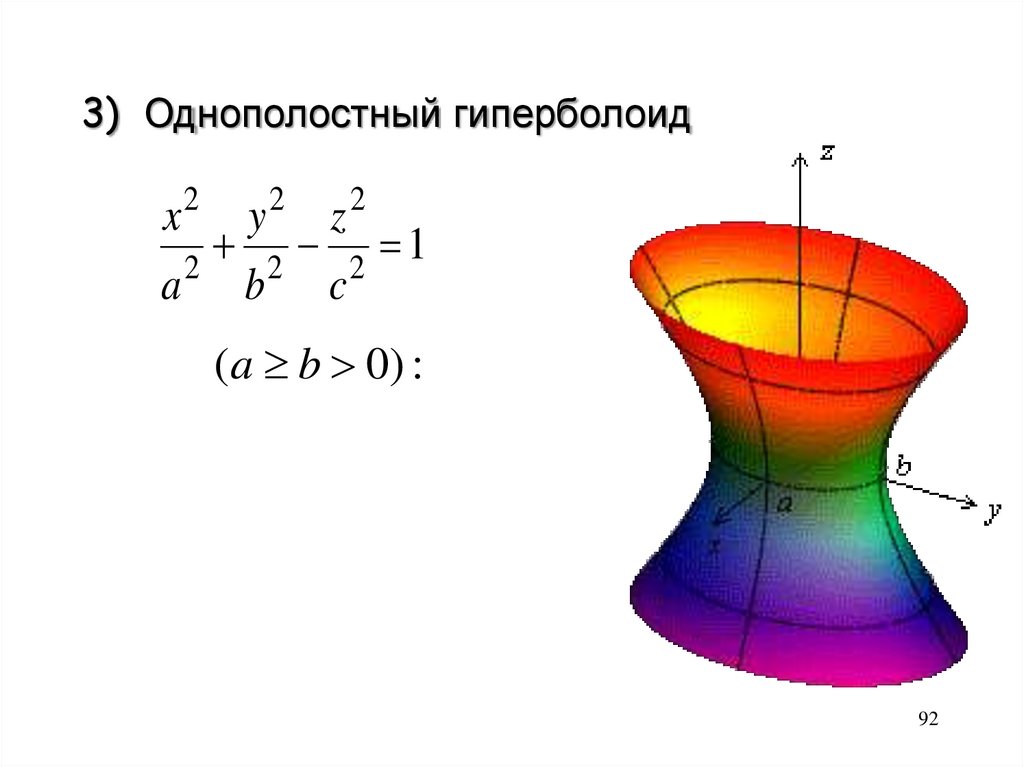
3) Однополостный гиперболоидx2
y2
a
b2
2
z2
c2
1
(a b 0) :
92
93.
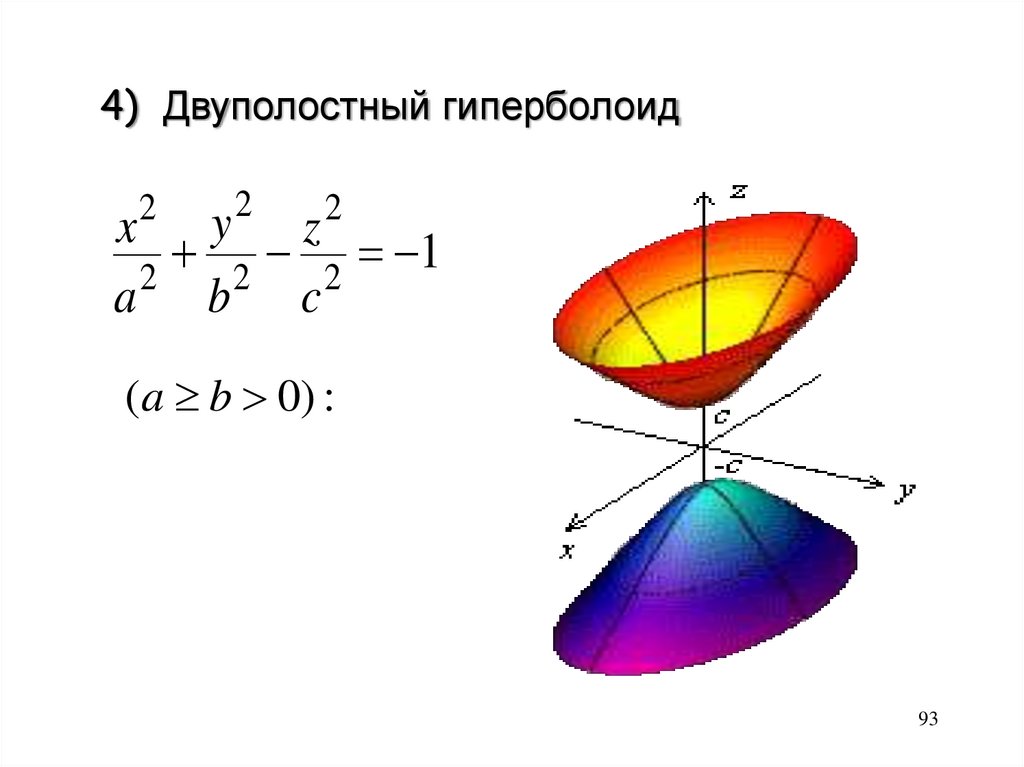
4) Двуполостный гиперболоид2
2
2
x y z
1
a2 b2 c2
(a b 0) :
93
94.
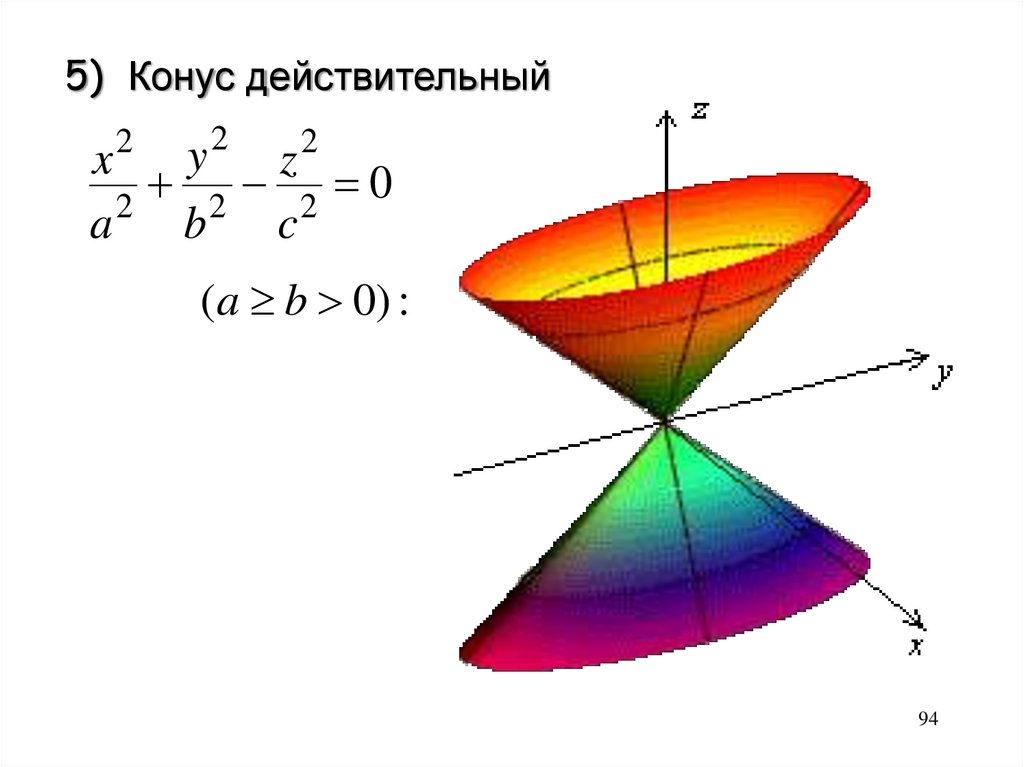
5) Конус действительный2
2
y
x
z2
0
2
2
2
a
b
c
(a b 0) :
94
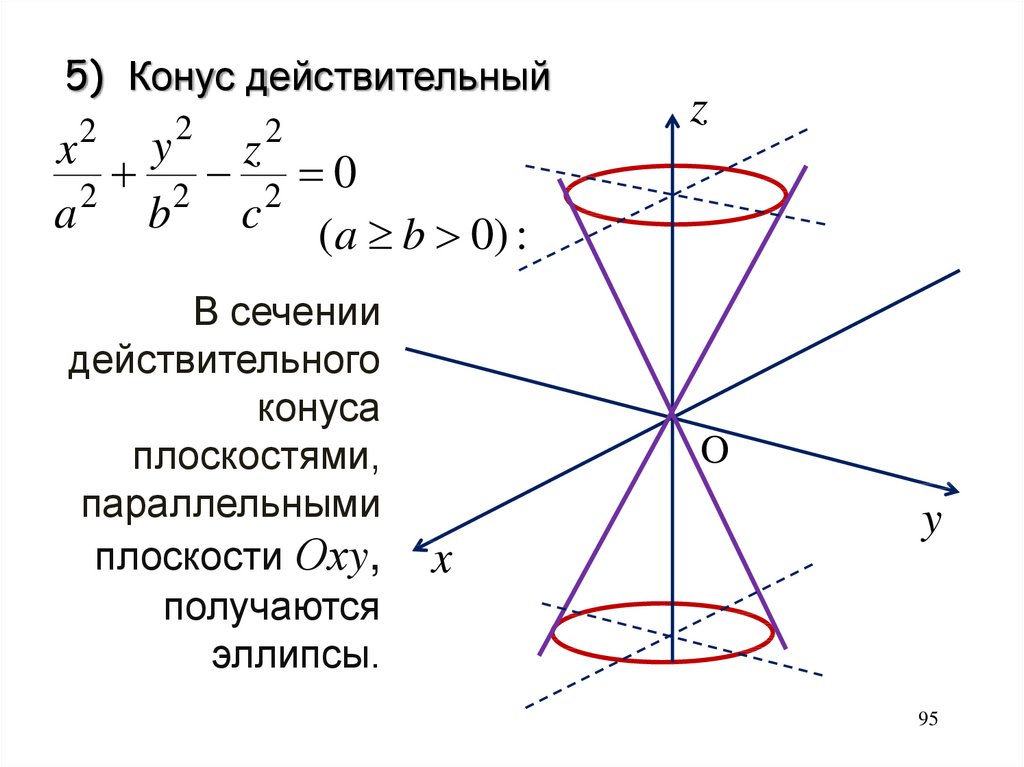
95.
5) Конус действительный2
x2 y
z2
2 2 0
2
a
b
c (a b 0) :
В сечении
действительного
конуса
плоскостями,
параллельными
плоскости Охy,
получаются
эллипсы.
z
O
x
y
95
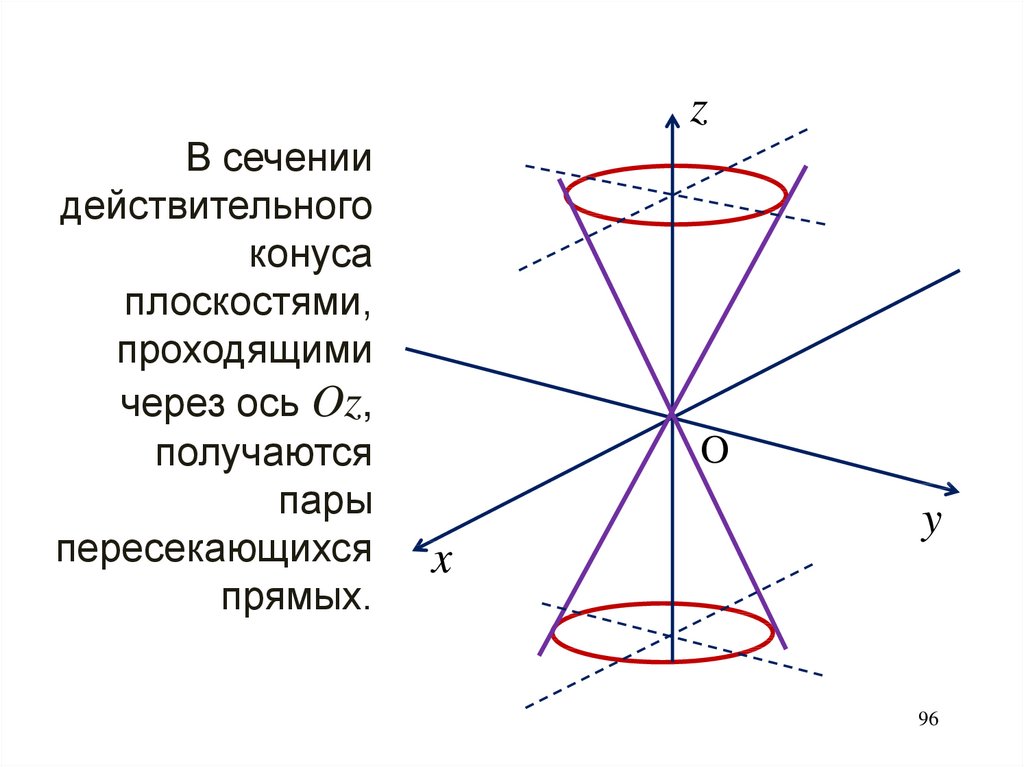
96.
zВ сечении
действительного
конуса
плоскостями,
проходящими
через ось Oz,
получаются
пары
пересекающихся
прямых.
O
x
y
96
97.
zВ сечении
действительного
конуса
плоскостями,
параллельными
оси Oz,
получаются
гиперболы…
O
x
y
97
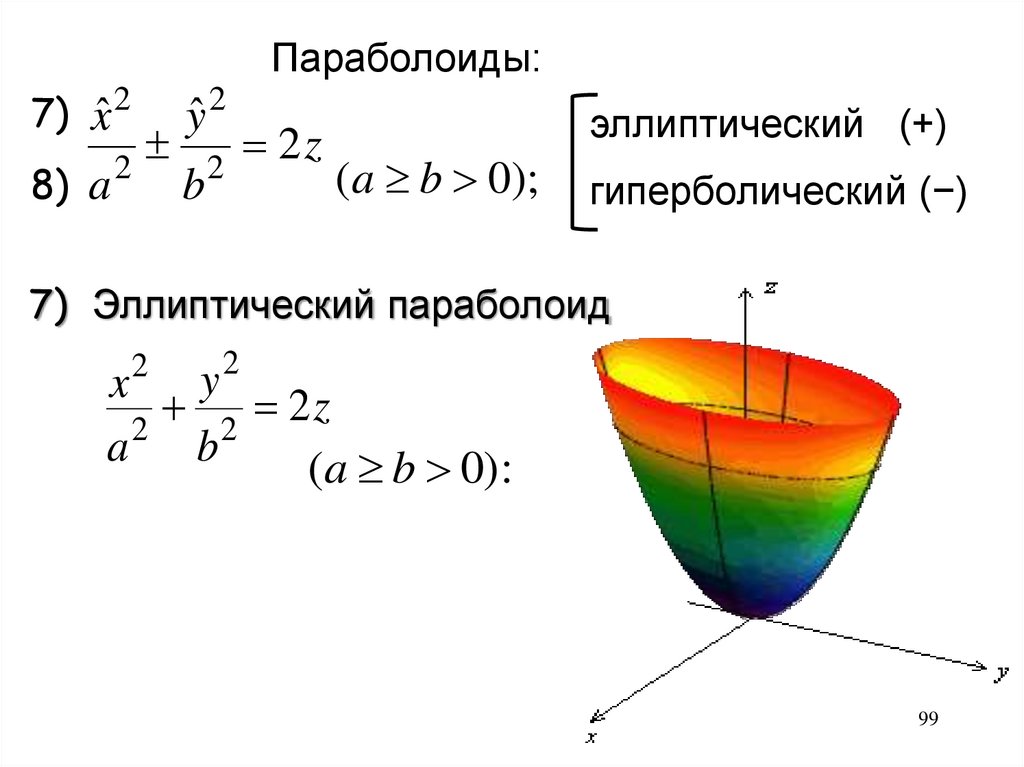
98.
Параболоиды:7) xˆ 2
8) a
2
ˆy 2
b
2
2z
эллиптический (+)
(a b 0);
гиперболический (−)
99.
Параболоиды:7) xˆ 2
8) a
2
ˆy 2
b
2
2z
эллиптический (+)
(a b 0);
гиперболический (−)
7) Эллиптический параболоид
2
2
y
x
2
z
a 2 b2
(a b 0):
99
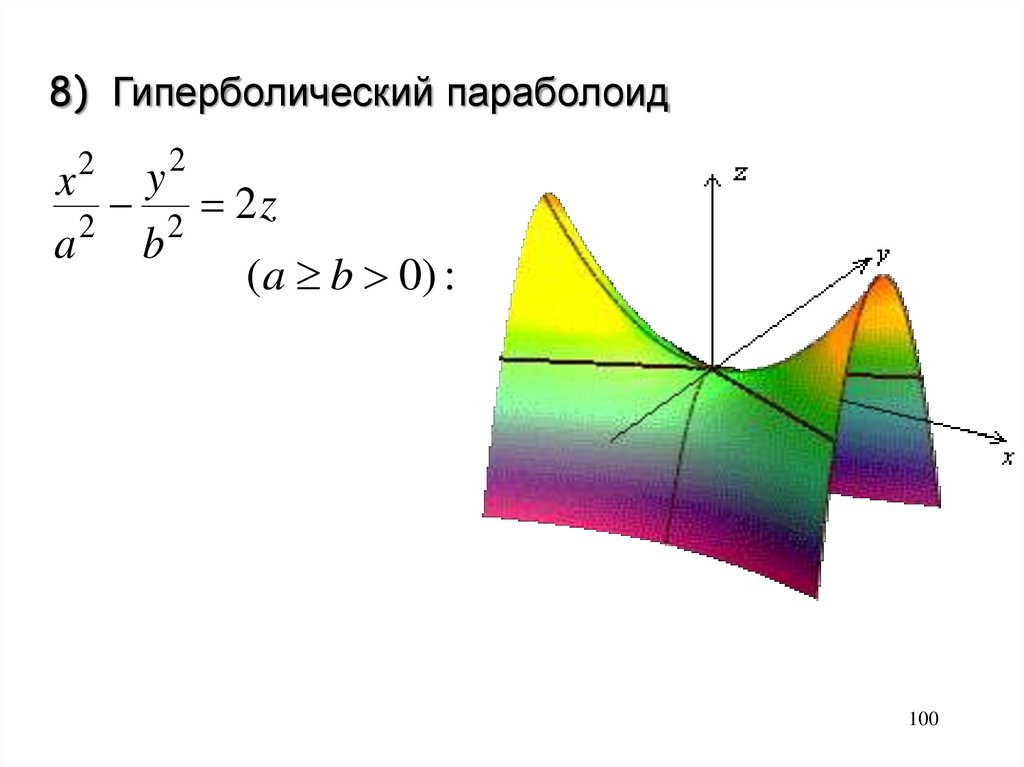
100.
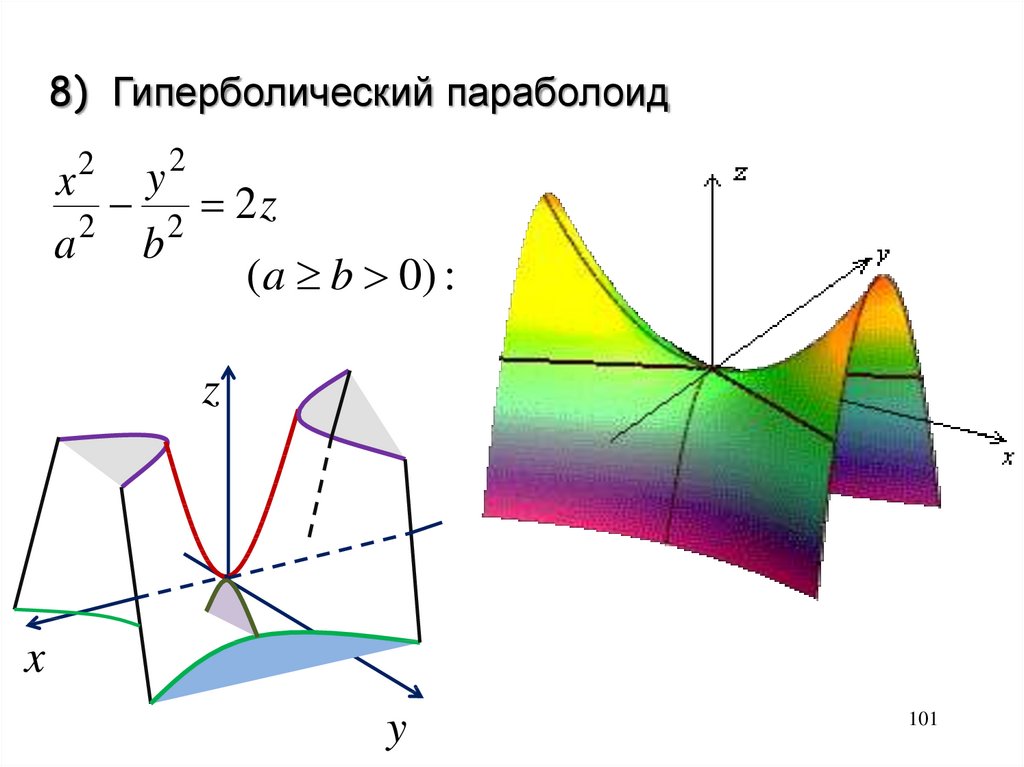
8) Гиперболический параболоид2
y
x
2 2z
2
a b
(a b 0) :
2
100
101.
8) Гиперболический параболоид2
y
x
2 2z
2
a b
(a b 0) :
2
z
x
y
101
102.
Цилиндры:9)
10)
2
2
эллиптические
yˆ
xˆ
2 1
2
a
b
действительный (−),
мнимый (+)
(a b 0) ;
102
103.
Цилиндры:9)
10)
2
2
эллиптические
yˆ
xˆ
2 1
2
a
b
действительный (−),
мнимый (+)
(a b 0) ;
xˆ 2 yˆ 2
11) гиперболический: 2 2 1;
a b
103
104.
Цилиндры:9)
10)
2
2
эллиптические
yˆ
xˆ
2 1
2
a
b
действительный (−),
мнимый (+)
(a b 0) ;
xˆ 2 yˆ 2
11) гиперболический: 2 2 1;
a b
2
14) yˆ 2 p xˆ ( p 0) − параболический;
104
105.
Цилиндры:9)
10)
2
2
эллиптические
yˆ
xˆ
2 1
2
a
b
действительный (−),
мнимый (+)
(a b 0) ;
xˆ 2 yˆ 2
11) гиперболический: 2 2 1;
a b
2
14) yˆ 2 p xˆ ( p 0) − параболический;
пары плоскостей:
105
106.
Цилиндры:9)
10)
2
2
эллиптические
yˆ
xˆ
2 1
2
a
b
действительный (−),
мнимый (+)
(a b 0) ;
xˆ 2 yˆ 2
11) гиперболический: 2 2 1;
a b
2
14) yˆ 2 p xˆ ( p 0) − параболический;
12)
13)
пары плоскостей:
пересекающихся
2
xˆ 2 yˆ
0
a 2 b2
(a b 0)
действительных (−),
мнимых (+);
107.
Цилиндры:9)
10)
2
эллиптические
2
yˆ
xˆ
2 1
2
a
b
действительный (−),
мнимый (+)
(a b 0) ;
xˆ 2 yˆ 2
11) гиперболический: 2 2 1;
a b
2
14) yˆ 2 p xˆ ( p 0) − параболический;
12)
13)
15)
16)
пары плоскостей:
пересекающихся
2
xˆ 2 yˆ
0
a 2 b2
(a b 0)
параллельных
yˆ a (a 0)
2
2
действительных (−),
мнимых (+);
действительных (−),
мнимых (+);
107
108.
Цилиндры:9)
10)
2
эллиптические
2
yˆ
xˆ
2 1
2
a
b
действительный (−),
мнимый (+)
(a b 0) ;
xˆ 2 yˆ 2
11) гиперболический: 2 2 1;
a b
2
14) yˆ 2 p xˆ ( p 0) − параболический;
12)
13)
пары плоскостей:
пересекающихся
2
xˆ 2 yˆ
0
a 2 b2
(a b 0)
параллельных
15)
16)
yˆ a (a 0)
17)
yˆ 0 − совпавших.
2
2
действительных (−),
мнимых (+);
действительных (−),
мнимых (+);
2
108
109.
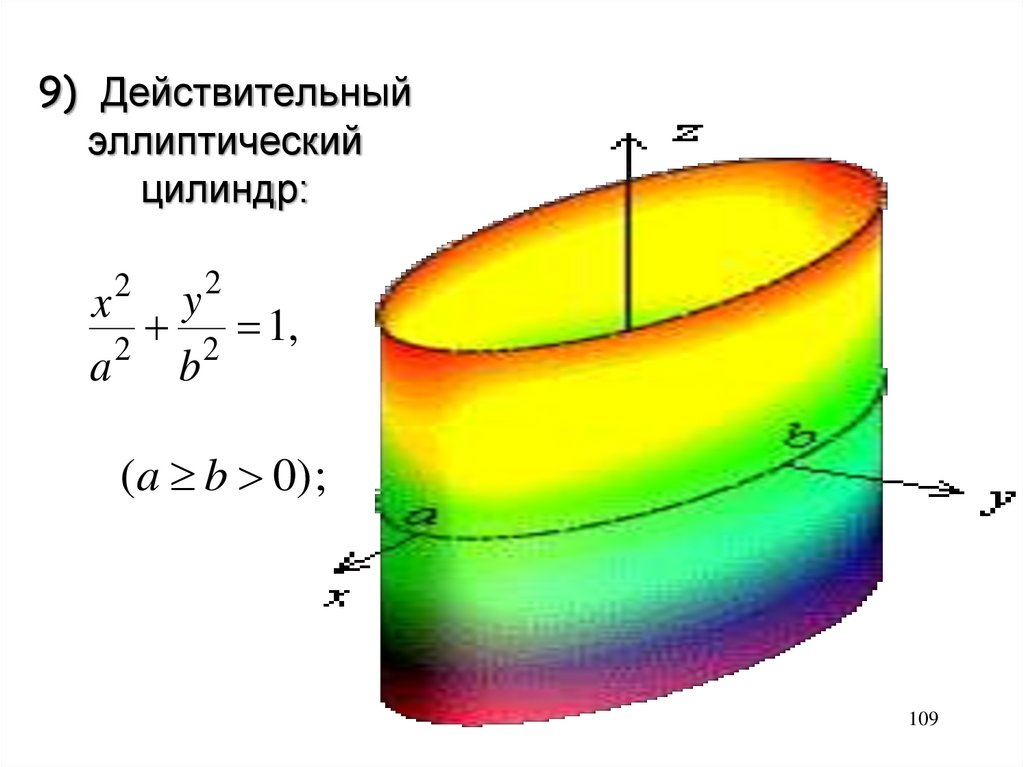
9) Действительныйэллиптический
цилиндр:
2
2
y
x
1
,
a 2 b2
(a b 0) ;
109
110.
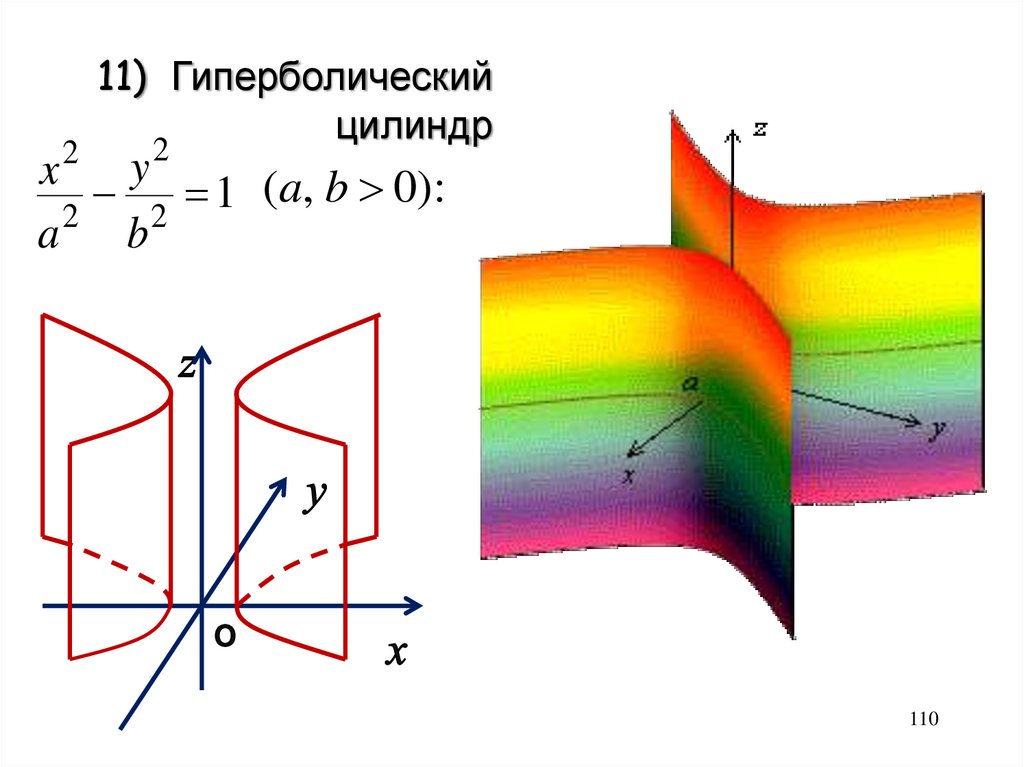
211) Гиперболический
цилиндр
2
y
x
(a, b 0):
1
a2 b2
110
111.
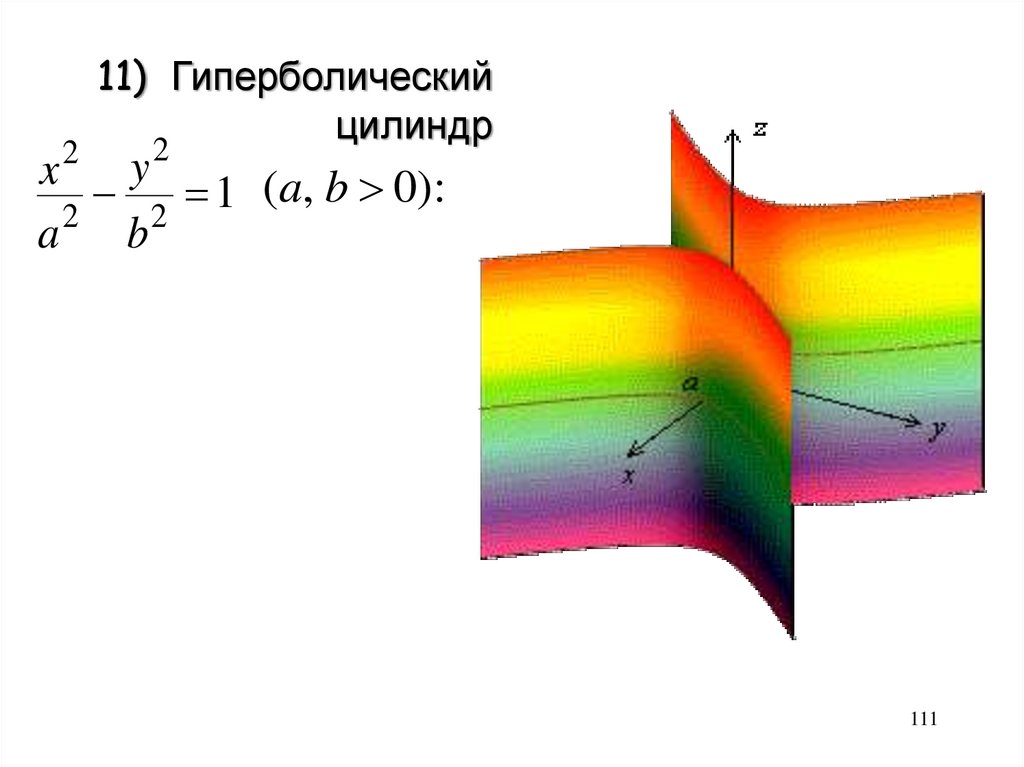
211) Гиперболический
цилиндр
2
y
x
(a, b 0):
1
a2 b2
111
112.
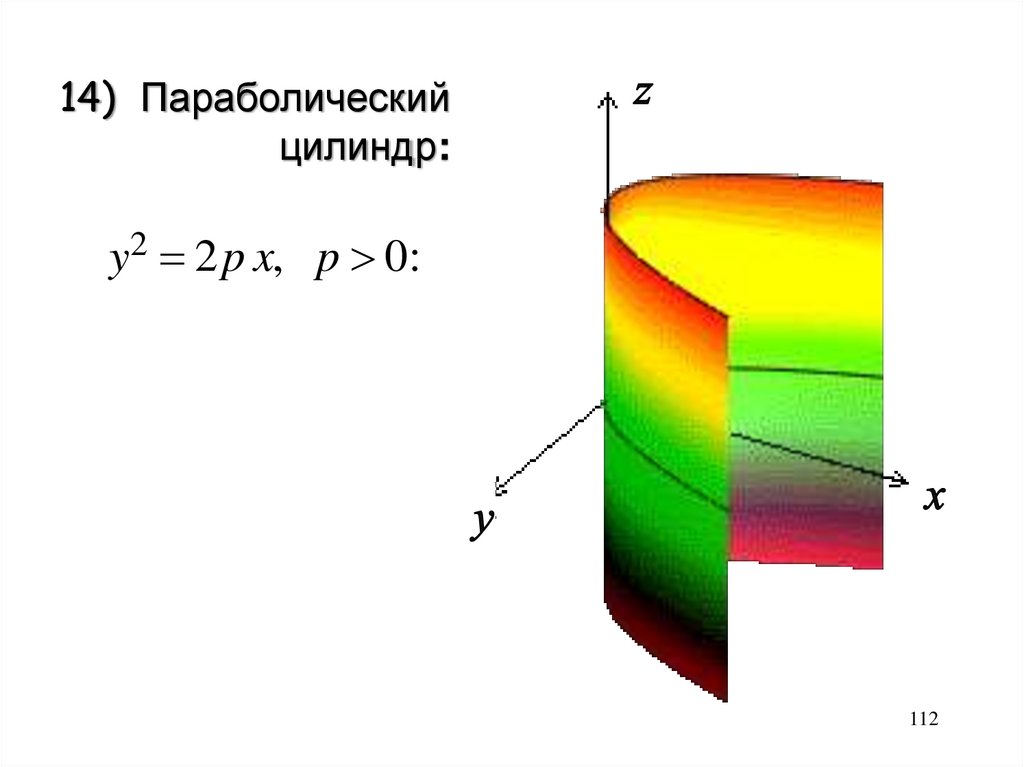
14) Параболическийцилиндр:
y2 2 p x, p 0:
112
113.
~ ~~ˆ
35.4. Система координат O, i , j , k ,
в которой
уравнение поверхности второго порядка имеет
канонический вид, называется канонической.
113
114.
~ ~~ˆ
35.4. Система координат O, i , j , k ,
в которой
уравнение поверхности второго порядка имеет
канонический вид, называется канонической.
Каноническая система координат определяется,
вообще говоря, неоднозначно.
114
115.
36. Квадрики в евклидовых пространствах36.1. Общее уравнение и матрица
Квадрикой в евклидовом пространстве называется
множество точек, задаваемое уравнением
n
n
n
a i j xi x j 2 b j x j c 0 ,
i 1 j 1
где
i 1
хi – координаты соответствующих векторов x
в ортонормированном базисе e (e1, ..., en )
евклидова пространства Е: x x1 e1 ... xn en .
Расширенной матрицей этой квадрики называют
115
116.
b1 Уравнение квадрикиможно переписать
~
A
. в матричном виде,
an1 an n bn
b b
x
c
1
1
n
~
( x1 , x2 , , xn ,1) A 0 ,
xn
1
а также в функциональной форме ( x ) 2 l ( x ) c 0 ,
где и b ─ квадратическая и линейная функции,
, l : E E , ( x ) x A x , l ( x ) b x .
матрицу a11 a1n
116
117.
36.2. Уравнение всякой квадрики в евклидовомпространстве можно привести к одному из трёх
(a) 1z12 ... r zr2 0 ,
видов:
(b) 1z12 ... r zr2 0 ,
(c) 1z12 ... r zr2 2 zr 1 0 ,
i 0 , 1 i r ;
, 0 ,
преобразованием неизвестных x T z c ,
T ортогональная матрица,
c координаты вектора сдвига
к новому началу координат.
117
118.
Благодаря п. 33.6 можем считать, что квадратичнаяформа (x ) приведена к главным осям
1 y12 ... r yr2 , i 0 (1 i r )
преобразованием неизвестных x Q y , Q
матрица перехода к ортонормированному базису f ,
fk собственный вектор соотв. симметрического
преобразования при собственном значении λk .
Тогда линейная часть уравнения
квадрики преобразуется по известному правилу
l ( x ) b 1 y 1 ... bn yn ,
(b 1, ..., bn ) (b1, ..., bn ) Q ,
118
119.
и всё уравнение в новых неизвестных приобретаетвид
1 y12 ... r yr2 2b 1 y1 ... 2b n yn c 0 .
Выделяя полные квадраты,
2
2
b
b
(
b
)
i
i
i
2
2
i yi 2b i yi i yi 2 yi
i
i i
2
2
b i
b
(
b
)
i
i
(1 i r ),
i yi
, и полагая zi yi
i
i
i
получаем уравнение
1z12 ... r zr2 2b r 1 yr 1 ... 2b n yn c 0 .
119
120.
Если b r 1 ... b n 0 , то уравнение приведеноИначе положим
к виду (a) или (b).
u b r 1 f r 1 ... b n f n 0 собственный вектор
при нулевом собственном значении, ортогональный
1
векторам f1, ..., f r . Систему векторов f1, ..., f r ,
u
|u |
дополним до ортонормированного базиса g ,
в котором уравнение квадрики приобретает вид
1z12 ... r zr2 2 yr 1 c 0 , 0 ,
и остается обозначить 2v yr 1 c 2 zr 1 .
120

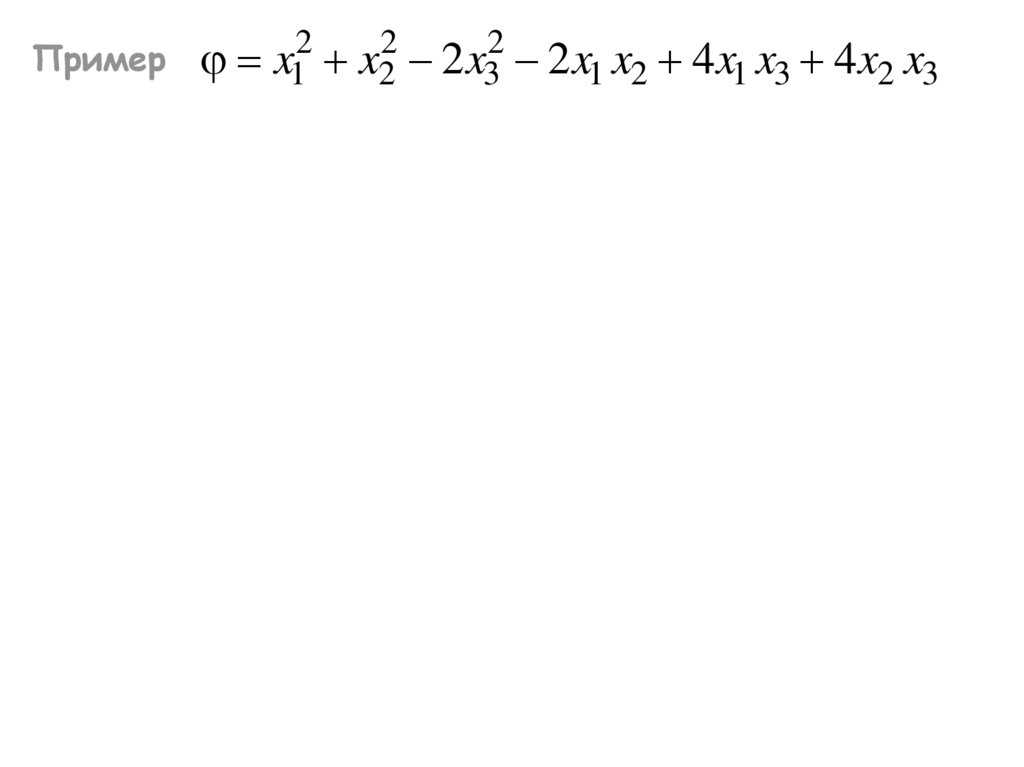
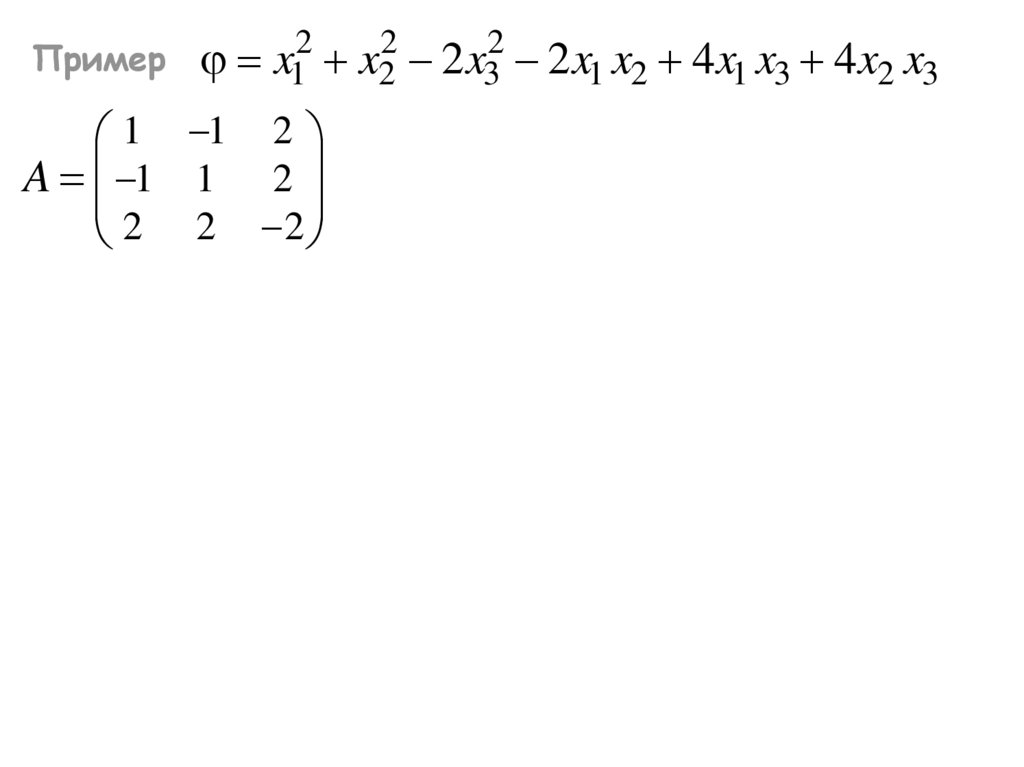




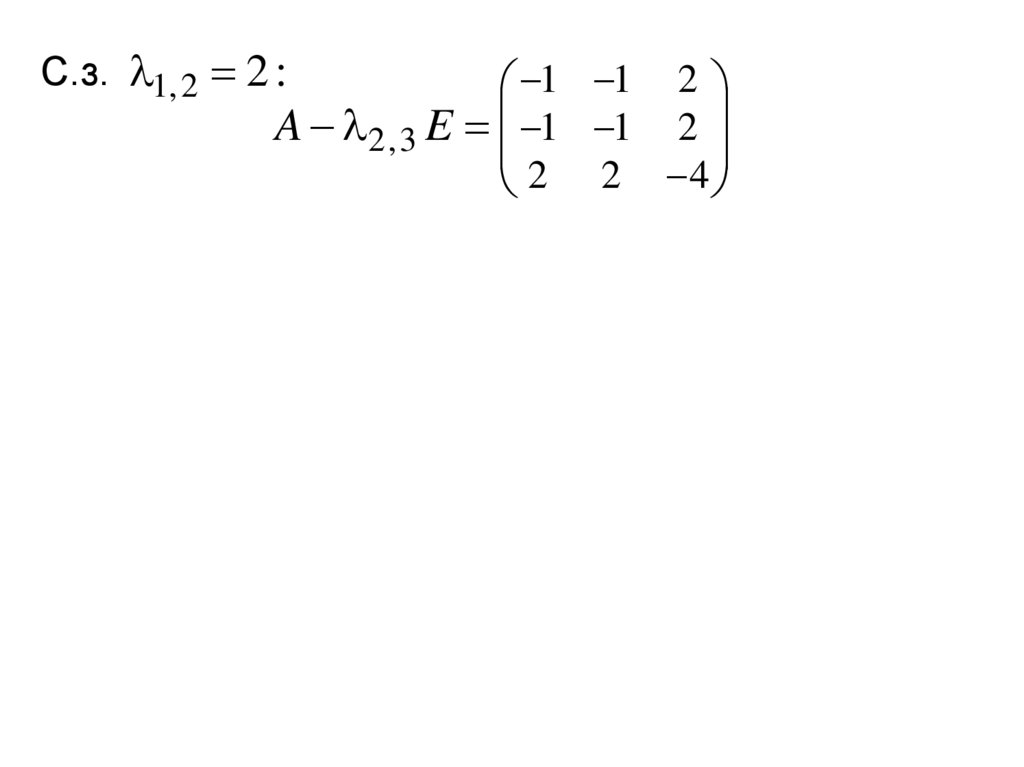
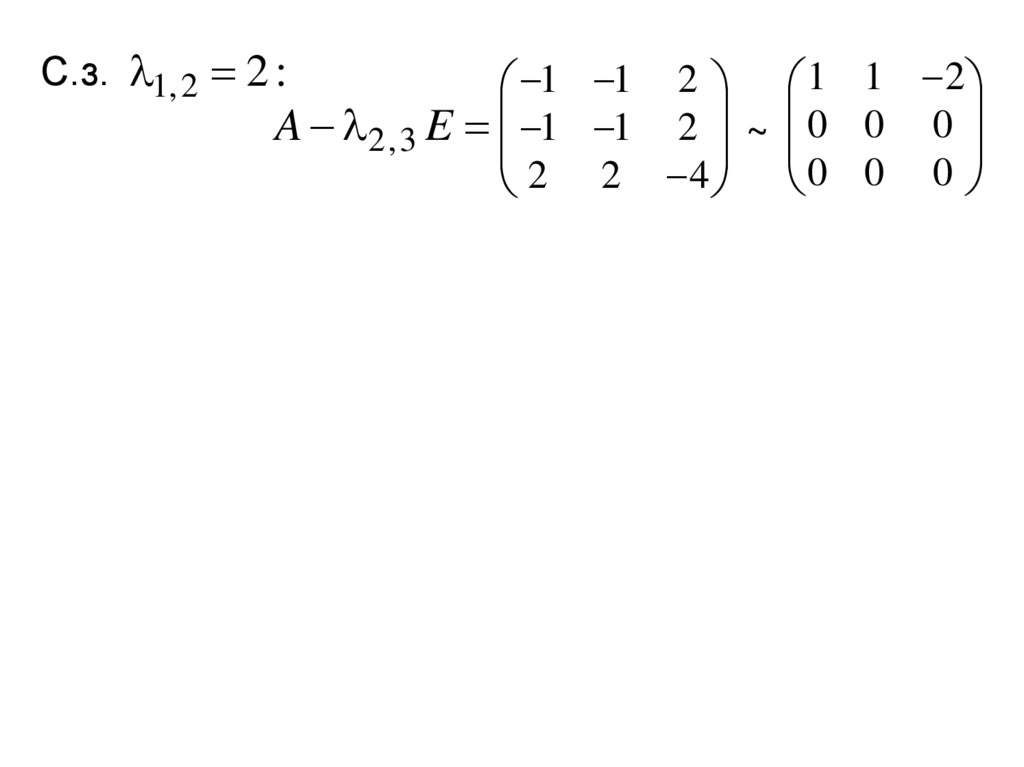








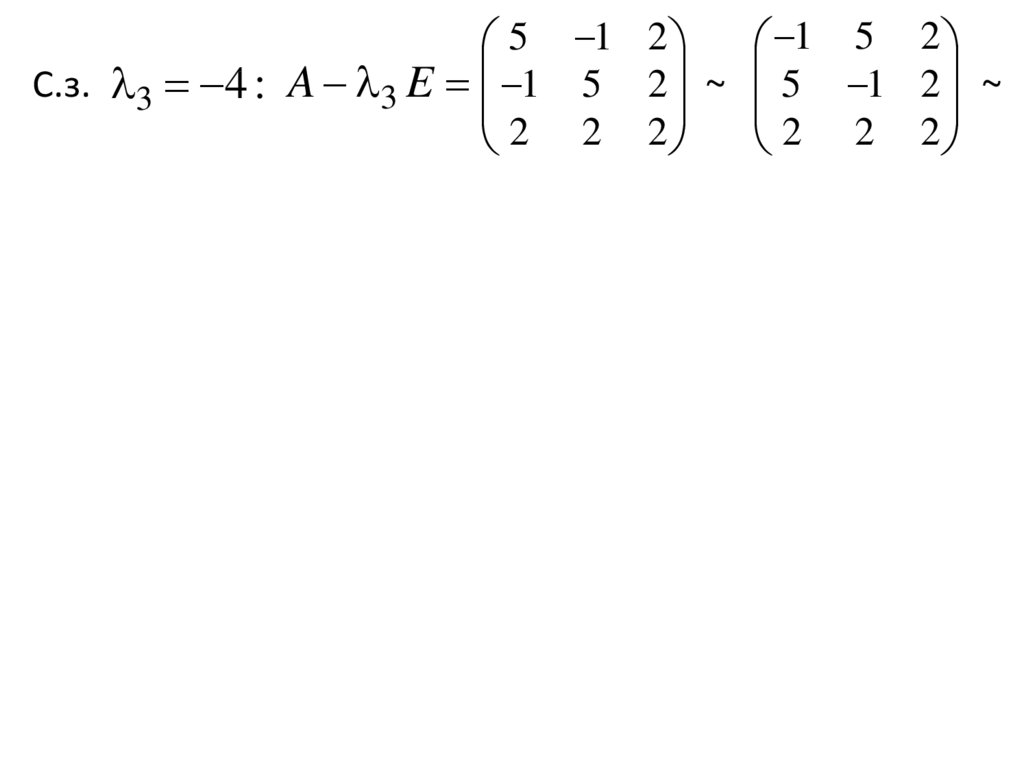
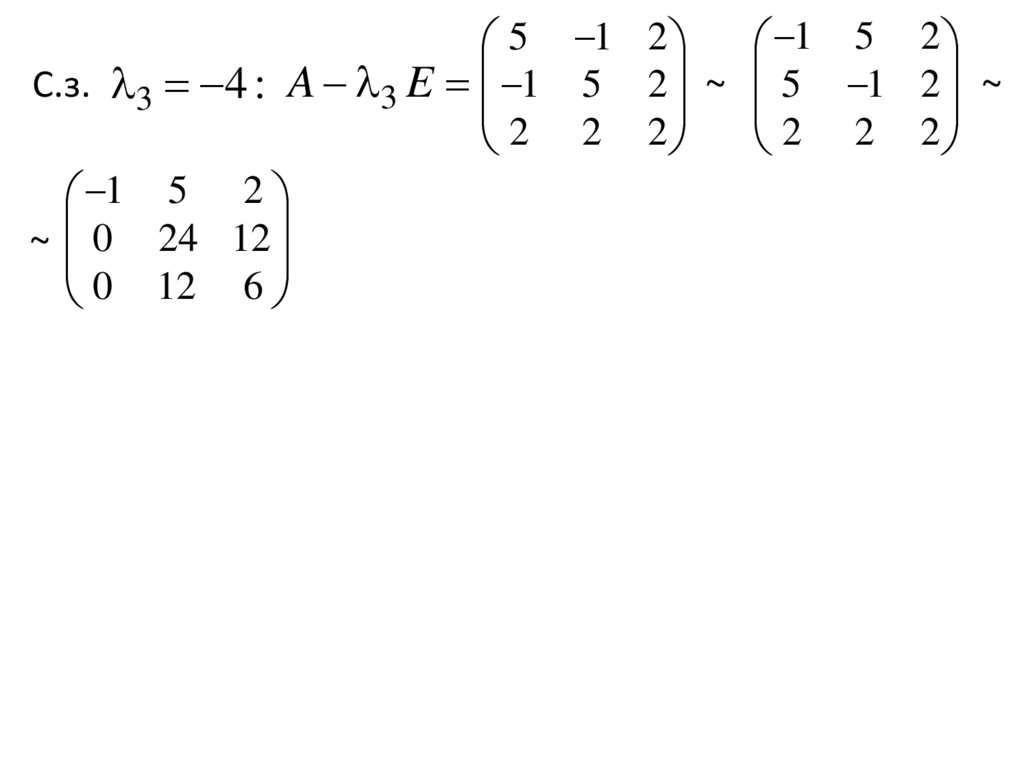
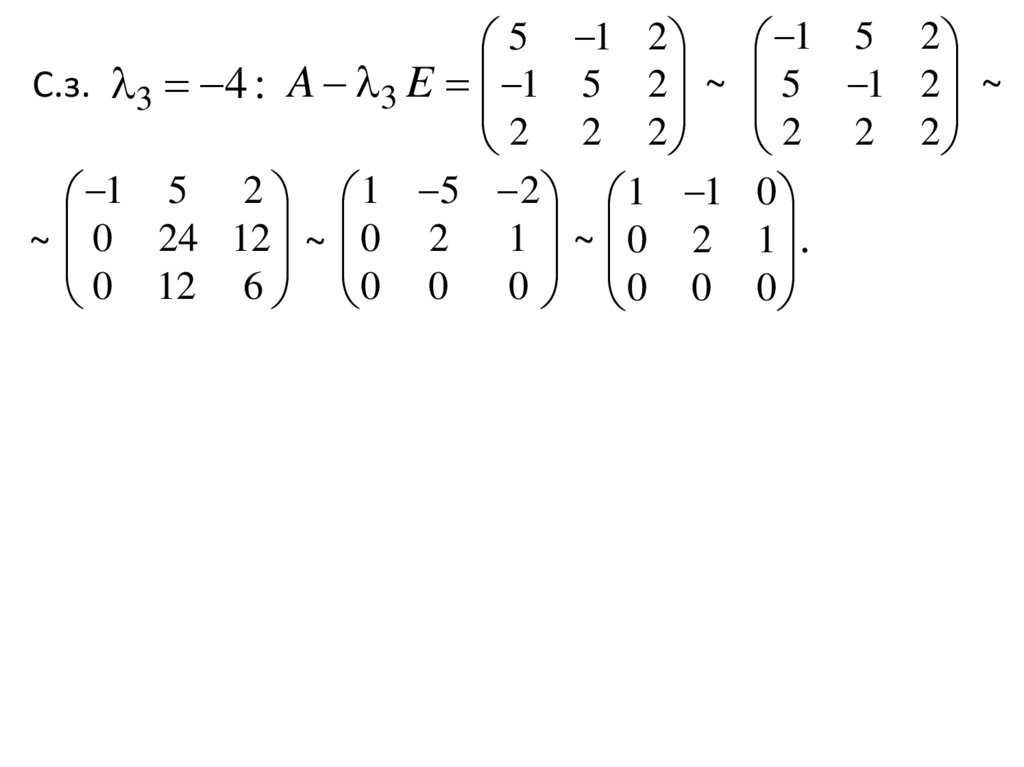









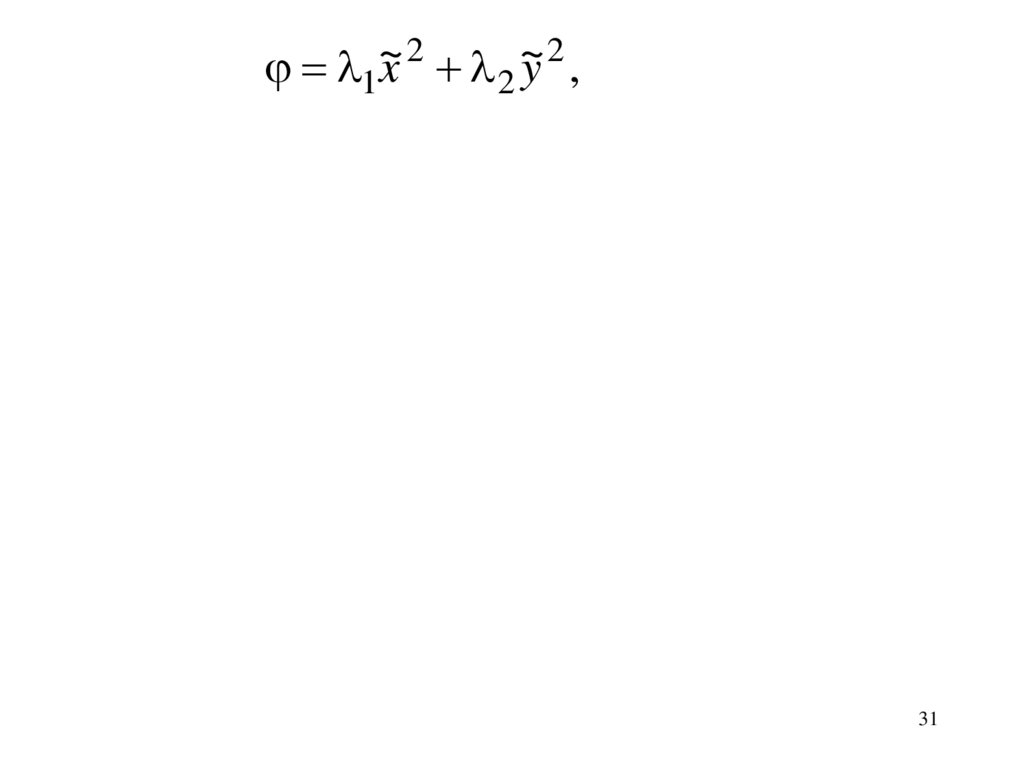





























































 Математика
Математика








