Похожие презентации:
Контрольная работа по дисциплине «Физическая химия». Раздел: «Электрохимия»
1.
Контрольная работа подисциплине «Физическая химия» раздел:
«Электрохимия»
3 курс 6 семестр
2.
Задание 1. Теория растворов сильных и слабых электролитовОпределите ионную силу водного раствора электролита А, если:
а) моляльная концентрация электролита А в растворе равна m;
б) моляльная концентрация электролита А в растворе равна m и в растворе
присутствует электролит В с концентрацией m1;
в) запишите уравнение предельного закона Дебая и Хюккеля и на основании
справочных данных [КС] о средних ионных коэффициентах активности
вычертите график зависимости от m = 0 до m = 3,0. На график нанесите
зависимость по предельному закону Дебая и Хюккеля.
г) По предельному закону Дебая и Хюккеля вычислите средний ионный
коэффициент активности при 298 К для раствора электролита А с
концентрацией m и раствора электролита А с концентрацией m, в котором
присутствует электролит В с концентрацией m1;
д) Определите средние ионные моляльность m± и активность a± при 298 К
раствора электролита А с концентрацией m и раствора электролита А с
концентрацией m, в котором присутствует электролит В с концентрацией m1.
3.
В качестве примера рассмотрим водный раствор хлорида натрия(электролит А = NaCl, моляльная концентрация m = 0.025 моль/кг H2O)
Уравнение для расчета ионной силы:
1 2
1
2
2
2
I mi zi (mNa z Na
m
z
)
Cl
Cl
2 i 1
2
Для симметричного электролита моляльные концентрации ионов и самого
электролита численно совпадают
mNa mCl mNaCl 0.025
поэтому ионная сила водного раствора хлорида натрия равна
1
I (0.025 12 0.025 12 ) 0.025
2
При добавлении в раствор хлорида натрия второго электролита В - Ca(NO3)2
m1 = 0,020 моль/кг H2O ионная сила раствора электролита А изменится и будет
равна
1 4
1
2
2
2
2
2
I mi zi (mNa z Na
m
z
)
m z m 2 z
2
Cl
Cl
Ca
Cl
Cl
Ca
2 i 1
2
4.
Концентрации катионов натрия и хлорид-ионов останется прежней m = 0.025моль/кг H2O), а концентрации катионов кальция и нитрат-ионов будут равны:
mСa2 mCa( NO3 )2 0.020
mNO 2 mCa( NO3 )2 2 0.020 0,040
3
Следовательно, ионная сила раствора, содержащего два электролита NaCl и
Ca(NO3)2 составит величину
I
1
(0.025 1 0.025 1 0.02 4 0.04 1) 0,085
2
Запишем уравнение предельного закона Дебая и Хюккеля
Коэффициент активности иона в данном растворе зависит только от заряда
иона и ионной силы раствора. Тогда в растворе, содержащем один электролит
NaCl с моляльной концентрацией m = 0.025 моль/кг H2O среднеионный
коэффициент активности равен
γ 10
0,5 z 2 I
0,834
а после добавления в раствор хлорида натрия второго электролита [В =
Ca(NO3)2 m1 = 0.020] нитрата кальция ионная сила раствора NaCl изменится и
будет равна
2 I
0
,
5
z
γ 10
0,715
5.
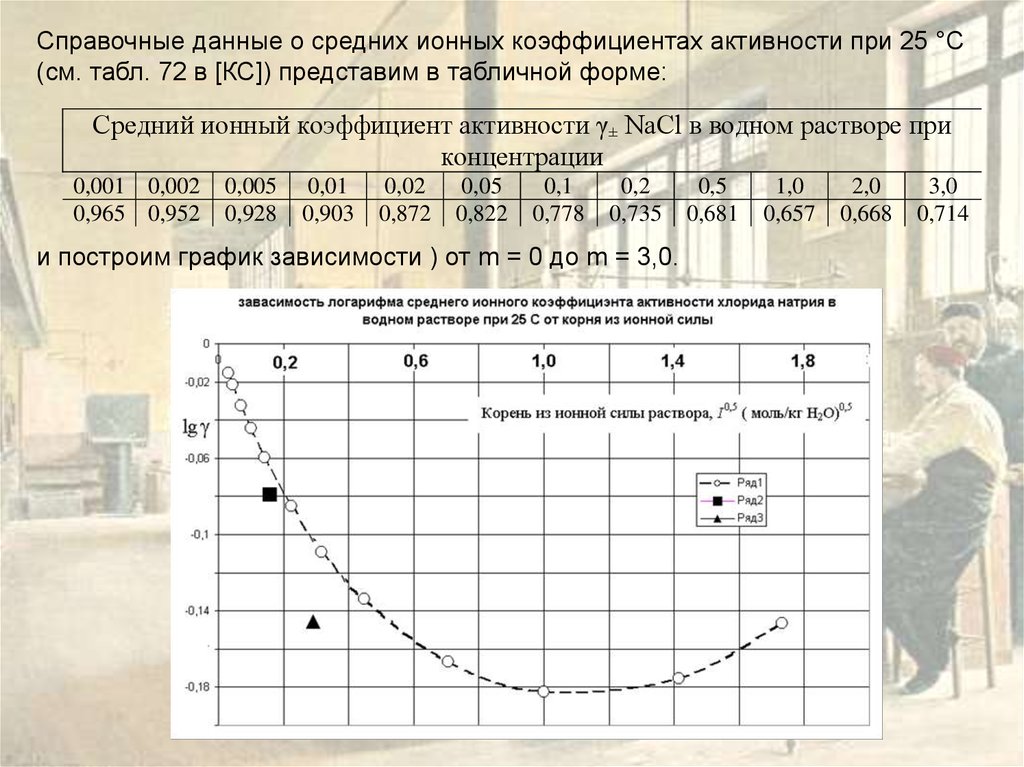
Справочные данные о средних ионных коэффициентах активности при 25 °С(см. табл. 72 в [КС]) представим в табличной форме:
Средний ионный коэффициент активности γ± NaCl в водном растворе при
концентрации
0,001 0,002
0,965 0,952
0,005
0,928
0,01
0,903
0,02
0,872
0,05
0,822
0,1
0,778
0,2
0,735
и построим график зависимости ) от m = 0 до m = 3,0.
0,5
0,681
1,0
0,657
2,0
0,668
3,0
0,714
6.
Для симметричного I – I-валентного электролита средняя ионная моляльностьm± раствора NaCl равна моляльной концентрации m.
Средняя ионная активность а± при 298 К раствора NaCl равна произведению
средних ионных величин моляльности и коэффициента активности
а± = m± ∙ ± = 0,025 ∙ 0,834 = 0,0208.
После добавления в раствор нитрата кальция средняя ионная активность
раствора NaCl будет равна
а± = m± ∙ ± = 0,025 ∙0,715 = 0,0179.
7.
Задание 2. Равновесия в водных растворах сильных и слабыхэлектролитов
Пользуясь справочными данными (см. табл.66 [КС]) для зависимости молярной
электрической проводимости раствора слабого электролита A от разведения
(1/C, л/моль):
а) постройте график зависимости концентрационной зависимости = f(С);
б) напишите уравнения, связывающие молярную, эквивалентную и удельную
электрические проводимости раствора электролита A и рассчитайте величины
удельной электрической проводимости раствора электролита A при известных
концентрациях;
в) постройте график концентрационной зависимости удельной электрической
проводимости;
г) графически определите удельную электрическую проводимость раствора
электролита А при концентрации СА и рассчитайте эквивалентную электрическую
проводимость раствора электролита А при этой концентрации;
д) напишите уравнение электролитической диссоциации электролита A;
е) пользуясь справочными данными (см.табл.65 на стр.123 [КС]) на основании закона
Кольрауша определите предельную эквивалентную электрическую проводимость в
растворе электролита А при бесконечном разбавлении (СА 0);
ж) рассчитайте степень диссоциации электролита A в растворе с концентрацией СА,
используя величины эквивалентной электрической проводимости при концентрациях
СА и СА 0 и определите рН водного раствора с концентрацией СА.
8.
Справочные данные для зависимости молярной электрической проводимости(μ) слабого электролита A = изо-C3H7COOH от разведения V при температуре
298 К [КС] поместим в таблицу, а затем определим (и запишем в эту же таблицу)
молярную концентрацию С = 1/V, величины эквивалентной ( , См моль-1 см2) и
удельной электропроводимости æ (См/см) для всех указанных в справочнике
значениях разведениях :
= æ/ Cэкв = Z = Z μ
где для изо-C3H7COOH значение Z = 1.
32
64
128
V = 1/C, л моль-1
C, моль·л-1
1/32
1/64
1/128
3,125
1,562
0,781
C 102, моль·л-1
11,4
15,9
104, См моль-1·м2 8,0
11,4
15,9
104, См моль-1 м2 8,0
250
178
124
æ 106, См см-1
( o изо-C3H7COO- = 34.2 104 См моль-1 м2).
256
1/256
0,39
22,2
22,2
86,7
512
1/512
0,195
30,8
30,8
60,2
1024
1/1024
0,0975
42,6
42,6
41,4
9.
На рисунках приведены графики концентрационных зависимостей удельнойæ = f(C) и эквивалентной = f(C) электрических проводимостей раствора,
построенные по данным таблицы
10.
11.
При заданной концентрации раствора С3 = 1,3∙10-3 графически определимудельную æ3 (См/см)
æ3 53·10-6 См см-1
и эквивалентную 3 (См моль-1 см2) электропроводность раствора
3 = 12,5 10-4 См моль-1 м2 = 12,5 См моль-1 см2
На основании данных справочника [КС] на основании закона Кольрауша
вычислим эквивалентную электропроводимость при бесконечном разведении o
(См моль-1 см2) при стандартной температуре 298 К.
λ 0 λ o, H λ o,изо -C H COO 3
7
λ0= (349.8 + 34.2) 104 = 384.0 104 См моль-1 м2
Рассчитаем степень диссоциации электролита А при концентрации С на
основании данных электрической проводимости
= / o = 12,5 10-4 / 384.0 10-4 = 0,032552 = 3,26 10-2 3,3 %
12.
Уравнение электролитической диссоциации слабого электролита в нашемслучае имеет вид:
изо-C3H7COOH H+ + изо-C3H7COO¯
Зная степень диссоциации электролита α, рассчитаем равновесные
концентрации ионов и недиссоциированных молекул в водном растворе при
концентрации С = 1,3∙10-3 моль/л, рН раствора и константу диссоциации
электролита:
[ H+ ] = α C = [изо-C3H7COO¯] = 0.0326 ∙1,3∙10-3 =4,23∙10-5 моль/л
pH = - lg [H+] = - lg (1,209∙10-4) = 4,37
K
[ H ][изо C3 H 7 COO _ ] α 2 C
0.0332 1.3 10 3
6
1
.
46
10
дисс
[изо C3 H 7 COOH ]
1 α
1 0.033
Полученное константы диссоциации значение находится в хорошем
соответствии со справочной величиной, равной 1.42 10-6 [КС]
13.
Задание 3. Расчет электродных потенциалов и ЭДС гальваническихэлементов, составленных из электродов 1 и 2 рода, редокс-электродов
Для гальванического элемента G:
a) напишите уравнения потенциалопределяющих реакций и уравнение Нернста
для расчета равновесных потенциалов левого и правого электродов;
б) определите средне-ионные активности электролитов в левом и правом
электродах и рассчитайте их равновесные значения потенциалов (моляльные
концентрации растворов указаны в таблице в скобках, величины средних ионных
коэффициентов активности при T = 298 К и стандартных электродных
потенциалов возьмите из справочника);
в) напишите электродные реакции, протекающие на левом и правом электродах
гальванического элемента G, полагая, что в электродной реакции участвует один
электрон;
г) найдите ЭДС гальванического элемента G и вычислите константу равновесия
реакции, протекающей самопроизвольно в гальваническом элементе при
температуре 298 К (в реакции участвует только один электрон).
14.
В качестве примера рассмотрим химический гальванический элемент :(-) Zn | ZnSO4 (m1) || KCl (m2) | AgCl(кр.) | Ag (+)
В соответствии с уравнением Нернста для вычисления равновесного
электродного потенциала электрода необходимо знать:
значение стандартного электродного потенциала Eº ,
температуру T,
число электронов z
активности ai,j веществ в окисленной и восстановленной формах, участвующих
в потенциалопределяющей электродной реакции.
Для левого электрода гальванического элемента уравнение
потенциалопределяющей реакции имеет вид:
Zn
2+
+ 2 ē Zn
EZn 2 / Zn E
o
Zn 2 / Zn
aZn 2
RT
ln
2F
aZn
Учитывая, что активность твёрдой фазы равна 1
EZn2 / Zn E
o
Zn 2 / Zn
RT
ln aZn2
2F
15.
Активность потенциалопределяющих ионов определить невозможно, поэтому еёприравнивают средней ионной активности электролита, создающего заданную
концентрацию ионов в растворе
aZn2 a , ZnSO4 m , ZnSO4 γ , ZnSO4 s mZnSO4 γ , ZnSO4
Для сульфата цинка коэффициент симметрии S = 1
EZn 2 / Zn E
o
Zn 2 / Zn
RT
RT
o
ln aZn 2 EZn 2 / Zn
ln mZnSO4 γ , ZnSO4
2F
2F
Средне-ионный коэффициент активности раствора сульфата цинка с моляльной
концентрацией m, согласно данным [КС], равен γ ,ZnSO4 0.387 , а стандартный
o
электродный потенциал E Zn
0.763В . Следовательно, для m1 = 0.01
2
/ Zn
электродный потенциал левого электрода при 298 К :
aZn 2 m , ZnSO4 γ , ZnSO4 mZnSO4 γ , ZnSO4 0.01 0.387 3.87 10 3
E Zn 2 / Zn
8.31 298
0.763
ln 0.01 0.387 0,906 В
96500
16.
Для правого электрода гальванического элемента уравнениепотенциалопределяющей реакции имеет вид:
-
AgCl + ē Ag + Cl
a AgCl
RT
o
E AgCl / Ag ,Cl E AgCl / Ag ,Cl
ln
1F
a Ag aCl
Принимая во внимание, что активности твёрдых фаз равны единичным
значениям aAg = 1 и aAgCl = 1, а активность хлорид-ионов:
a
a , KCl s m KCl , KCl
RT
RT
o
ln a , KCl E AgCl / Ag ,Cl
ln mKCl , KCl
F
F
,Cl
o
E AgCl / Ag ,Cl E AgCl
/ Ag , Cl
o
E AgCl
0.222 В
/ Ag , Cl
Согласно [КС]
a
,Cl
E AgCl / Ag ,Cl
, KCl 0.770
a ,KCl s mKCl ,KCl 0.1 0.77 0.077
8.31 298
0.222
ln 0.1 0.770 0,156 В
96500
17.
Результаты расчетов показывают, чтоE AgCl / Ag ,Cl E Zn 2 / Zn
Поэтому при замыкании гальванического элемента на нагрузку, электроны в
цепи будут перемещаться от электрода с меньшим значение потенциала, к
электроду с большим его значением, т.е. на левом и на правом электродах
гальванического элемента будут протекать окислительно-восстановительные
процессы согласно следующим уравнениям
на левом электроде: ½ Zn - ē ½ Zn2+
на правом электроде: AgCl + ē Ag + ClТогда суммарно в гальваническом элементе при замыкании цепи на нагрузку
будет самопроизвольно протекать электрохимическая реакция вида
AgCl + ½ Zn Ag + Cl- + ½ Zn2+
ЭДС E E AgCl / Ag ,Cl ЕZn2 / Zn 1.062B
18.
Вычислим константу равновесия реакции, протекающей самопроизвольно вгальваническом элементе при температуре 298 К. В реакции участвует только
один электрон
ЭДС (станд) E o E o AgCl / Ag ,Cl E o Zn 2 / Zn 0.985 B
o
G298
RT ln K a , 298
o
G298
z F Eo
Ка,298 = ехр(z F E0/(RT)) = 4.68·1016
19.
Задание 4. Составьте гальванический элемент, в котором протекаетсамопроизвольно химическая реакция А
Напишите уравнение, связывающее стандартное изменение энергии Гиббса в
ходе химической реакции, протекающей в гальваническом элементе, со
стандартным значением ЭДС гальванического элемента при температуре 305
К.
Определите:
а) стандартное значение ЭДС гальванического элемента, в котором протекает
химическая реакция А, при температуре 298 К на основании значений
стандартных электродных потенциалов из (КС);
б) стандартное значение ЭДС E°T при температуре Т на основании значения
E°298 при 298 К и величины , приняв, что в указанном интервале температур
зависимость E° = f (T) линейна.
в) изменение энтальпии (тепловой эффект) (кДж), энтропии (Дж/К), энергию
Гиббса (кДж) и константу равновесия Ка для реакции А, протекающей в
гальваническом элементе при температуре Т.
20.
Пусть в гальваническом элементе протекает самопроизвольно химическаяреакция
Pb + 2 AgI = PbI2 + 2 Ag
Потенциал определяющие реакции:
PbI2 + 2 ē Pb + 2 I
2AgI + 2 ē 2 Ag + 2 I-
o
EPbI
2 / Pb, I
0.365В
o
E AgI
0.152 В
/ Ag , I
Стандартное изменение энергии Гиббса GT° в ходе химической реакции,
протекающей в гальваническом элементе связано со стандартным значением
ЭДС при заданной температуре Т = 288 К выражением
o
G288
z F E o 288
Стандартное значение ЭДС гальванического элемента, в котором протекает
химическая реакция, при температуре Т = 298 К на основании значений
стандартных электродных потенциалов из [КС] равно
o
o
o
E298 E AgI
E
/ Ag , I
PbI
2 / Pb , I
0.152 ( 0.365) 0.213В
21.
Найдем стандартное значение ЭДС при температуре Т на основании значенияЕ° при 298 К и величины
-4
(ΔЕ°/ΔТ)p = -1.38·10 В/К
приняв, что в указанном интервале температур зависимость E°= f(T) линейна
E
o
o
dT 0,213 1,38 10 4 10 0,212В
E E298
T
T P
Зная стандартное значение ЭДС, легко определить изменение энергии Гиббса
GT° (кДж) для реакции А, протекающей в гальваническом элементе при
температуре Т = 288 К.
o
G288
z F E 288
= – 2∙ 96500∙ 0.212 = – 40916 Дж
Изменение энтропии ST° (Дж/К) реакции при температуре Т определим на
основании уравнения
o
S 288
o
G288
dE
4
zF
2
96500
(
1
,
38
10
) 26,634 Дж / К
dT
T P
22.
Определим тепловой эффект HT° (кДж) химической реакции А при температуреИз уравнения Гиббса – Гельмгольца следует
dE
dE
о
zF T
E 288
dT
dT
2 96500 ( 288 1.38 10 4 0.212 ) -48587 Дж
o
о
H 288
z F E 288
zFT
Тогда константа равновесия Кa химической реакции при температуре Т равна:
o
K a , 288 exp( G288
/ RT )
K a , 288 exp( 40842,7 /(8.31 288) 2,45 10 7






















 Химия
Химия