Общие положения уравнительных вычислений. Многократно измеренная величина. Измерения в структурах

1. 1. Общие положения уравнительных вычислений

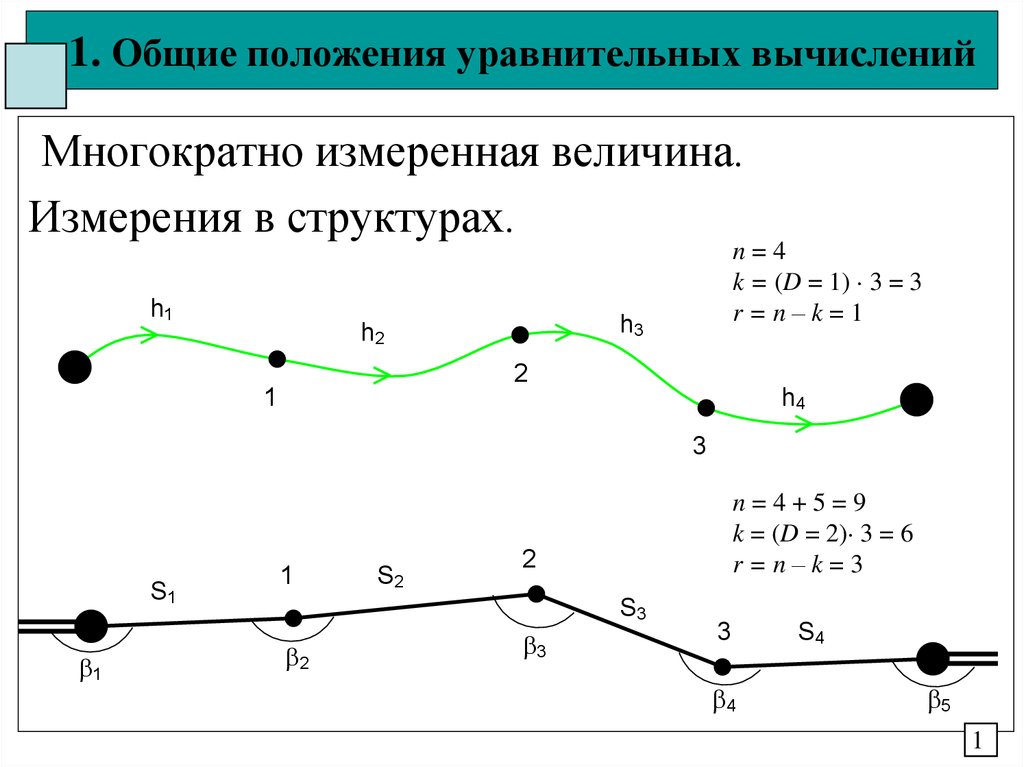
Многократно измеренная величина.
Измерения в структурах.
h1
n=4
k = (D = 1) 3 = 3
r=n–k=1
h3
h2
2
1
h4
3
S1
1
1
S2
n=4+5=9
k = (D = 2) 3 = 6
r=n–k=3
2
S3
2
3
3
4
S4
5
1

2. 1. Общие положения уравнительных вычислений

Условия возникновения задачи обработки в структурах
(геодезических построениях):
-Наличие избытка r;
-Погрешности измерений .
Наличие избытка – возникновение математических
условий r = n – k.
Наличие избытка – неопределенность, оценка качества.
Избыток – погрешности – обработка.
Обработка: количество (уравнивание)
качество (оценка точности)
2

3. 1. Общие положения уравнительных вычислений

Общая постановка задачи:
Измерено n величин yi (их истинные значения Yi).
Необходимых измерений надо k (k < n). Избыток
r = n – k – число строгих математических
условий вида
f1(Y1, Y2, …, Yn ) = 0
……………….
fr(Y1, Y2, …, Yn ) = 0
Уравнения независимы. Называются
уравнениями математической связи.
3

4. 1. Общие положения уравнительных вычислений

Замена Yi на yi дает
f1(y1, y2, …, yn ) = W1
……………….
fr(y1, y2, …, yn ) = Wr
-r невязок. Невязки не 0 т.к. измерения yi c
погрешностями.
Первое правило обработки – проверка качества
измерений сравнением невязки с допуском. Не
лучший вариант (не 100 %!).
4

5. 1. Общие положения уравнительных вычислений

Главная задача обработки – устранение невязки
(и от неё неопределенности).
Выполнение – введение в измерения поправок
vi.Исправленные измерения
yˆ i = yi + vi → Yi
Тогда уравнения связи будут
f1(y1 + v1, y2 + v2, …, yn + vn) = 0
……………….
fr (y1 + v1, y2 + v2, …, yn + vn) = 0
Повышение точности после обработки.
5

6. 1. Общие положения уравнительных вычислений

Просто задача не решаема т.к. r < n –
недоопределенная система. Для решения
привлекается дополнительная вероятностная
информация:
Запишем вероятность появления вместе всех
погрешностей i c НЗР вида
1
f ( )
P ( 1 , 2 ,..., n )
e
1 2
2
2
2 2
1 1
12
2 ... 2
1
d n
2 1
1 d 1
e
...
n
1
n
2
6

7. 1. Общие положения уравнительных вычислений

Наиболее вероятна та совокупность
2
погрешностей для которой Р = max – 2 min
Замена на v дает дополнительное условие
2 v 2 02 2
2
Ô min
v
pv
2 2 2
Условие позволяет получить наилучшую
комбинацию поправок для уничтожения невязок.
Это есть принцип МНК.
Учитывать v = -
7

8. 1. Общие положения уравнительных вычислений

Очевидные достоинства МНК:
-ограничение крупных поправок;
-при равноточных измерениях поправки
распределяются достаточно равномерно
-при неравноточных веса уменьшают поправки к
более точным, увеличивают к менее точным.
Недостатки:
-зависимость от НЗР
-зависимость от нарушения т. Ляпунова
8

9. 1. Общие положения уравнительных вычислений

Основные способы решения поставленной
задачи обработки – сведение задачи оценивания
к задаче поиска экстремума целевой функции Ф.
Из методов поиска выделяют:
-метод безусловного поиска Эйлера;
-метод условного поиска Лагранжа.
- обобщённый способ
Эйлер – параметрический способ.
Лагранж – коррелатный способ.
9

10. 1. Общие положения уравнительных вычислений

Постановка задачи при коррелатном способе
оценивания:
r уравнений связи после замены истинных
величин измеренными и введением поправк для
устранения невязок будут
f1(y1 + v1, y2 + v2, …, yn + vn) = 0
……………….
fr (y1 + v1, y2 + v2, …, yn + vn) = 0
Тогда сведение к минимизации будет такое
12

11. 1. Общие положения уравнительных вычислений

Ф = [pv2] = min
НО - при выполнении r принятых выше условий.
Условный экстремум - на основе функции
Лагранжа вида
Ф(v1, v2, …, yn ) = [pv2] + 1 f1 + …+ k fr
Решение задачи минимизации производится
обычными, известными способами.
Оценивание-минимизация-поправки в
измерения.
13

12. 1. Общие положения уравнительных вычислений

Постановка задачи оценивания в
параметрическом способе:
Выбирают k независимых параметров Тi через
которые однозначно и легко можно выразить все
измерения Yi:
Yi = fi(Т1, Т2,…, Тk)
Замена истинных измерений на реальные дает
yi + vi = fi(t1, t2,…, tk)
ti – уравненные (не истинные параметры)
10

13. 1. Общие положения уравнительных вычислений

Теперь
vi = fi(t1, t2,…, tk) - yi
и сведение к безусловному экстремуму
Ф pv p( f (t1 ,..., t k ) x) min
2
2
Находится достаточно просто.
В качестве параметров могут быть как
измеренные так и другие величины, однозначно
и просто позволяющие выразить измерения.
Прямой и косвенный подход.
Линейная, линеаризованная и нелинейная формы11
.

14. 1. Общие положения уравнительных вычислений

При оценке качества (оценке точности)
выделяют:
оценку точности измерений до уравнивания,
-оценку точности измерений после уравнивания,
- оценку точности параметров,
- оценку точности функций от уравненных величин.
Задача может решаться на основе формулы
ковариационной матрицы
Кх = МО((х – МО(х)) (х – МО(х))Т),
где х – величина для оценки точности, но чаще на
основе ФТПП для функции F: KF = f KY fT
14