Похожие презентации:
Геометрическая задача на вычисление
1. Геометрическая задача на вычисление
Окружности
Углы
Четырёхугольники
Треугольник
2. Окружность
Надо вспомнить:ОКРУЖНОСТЬ И КРУГ
СВОЙСТВА ХОРД
УГЛЫ И ОКРУЖНОСТЬ
ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ
ДЛИНЫ И ПЛОЩАДИ
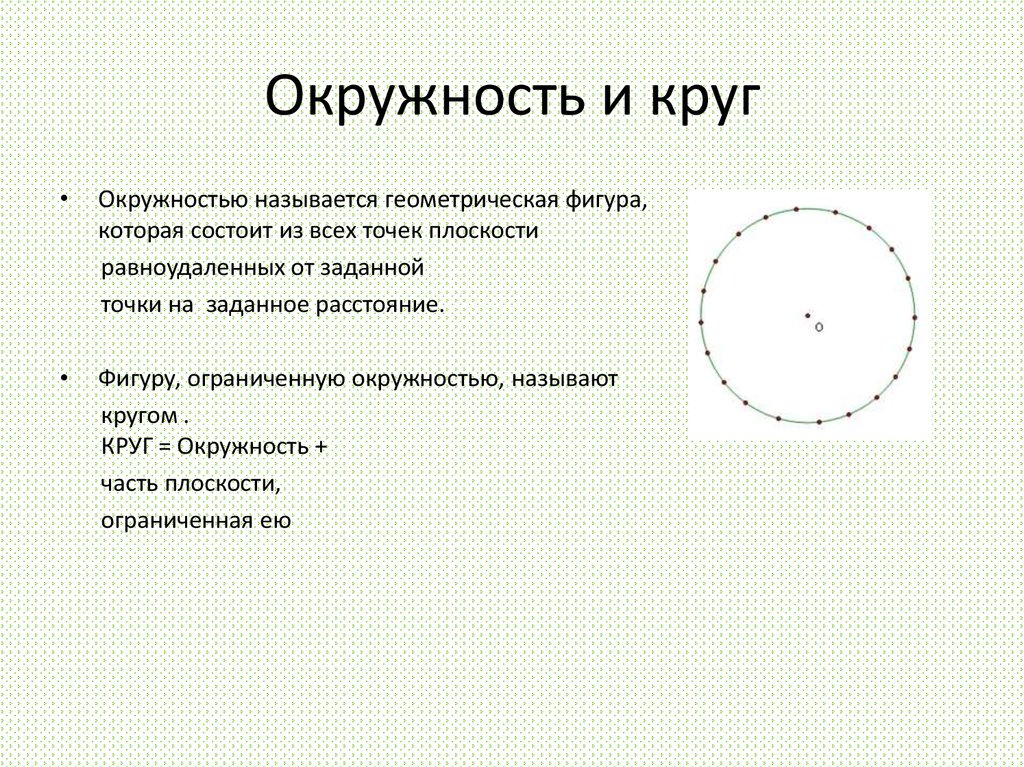
3. Окружность и круг
Окружностью называется геометрическая фигура,
которая состоит из всех точек плоскости
равноудаленных от заданной
точки на заданное расстояние.
Фигуру, ограниченную окружностью, называют
кругом .
КРУГ = Окружность +
часть плоскости,
ограниченная ею
4. Свойства хорд
Если хорды равноудалены от центра окружности, то они равны.
Если хорды равны, то они равноудалены от центра окружности.
Большая из двух хорд находится ближе к центру окружности.
Наибольшая хорда является диаметром.
Если диаметр делит хорду пополам, то он перпендикулярен ей.
Если диаметр перпендикулярен хорде, то он делит ее пополам .
Равные дуги стягиваются равными хордами.
Дуги, заключенные между параллельными хордами, равны.
Все вписанные углы, опирающиеся на одну и ту же дугу, раны.
Все вписанные углы, опирающиеся на одну и ту же хорду, вершины
которых лежат по одну сторону от этой хорды, равны.
• Все вписанные углы, опирающиеся на диаметр, прямые.
• Любая пара углов, опирающихся на одну и ту же хорду, вершины
которых лежат по разные стороны хорды, составляют в сумме 180.
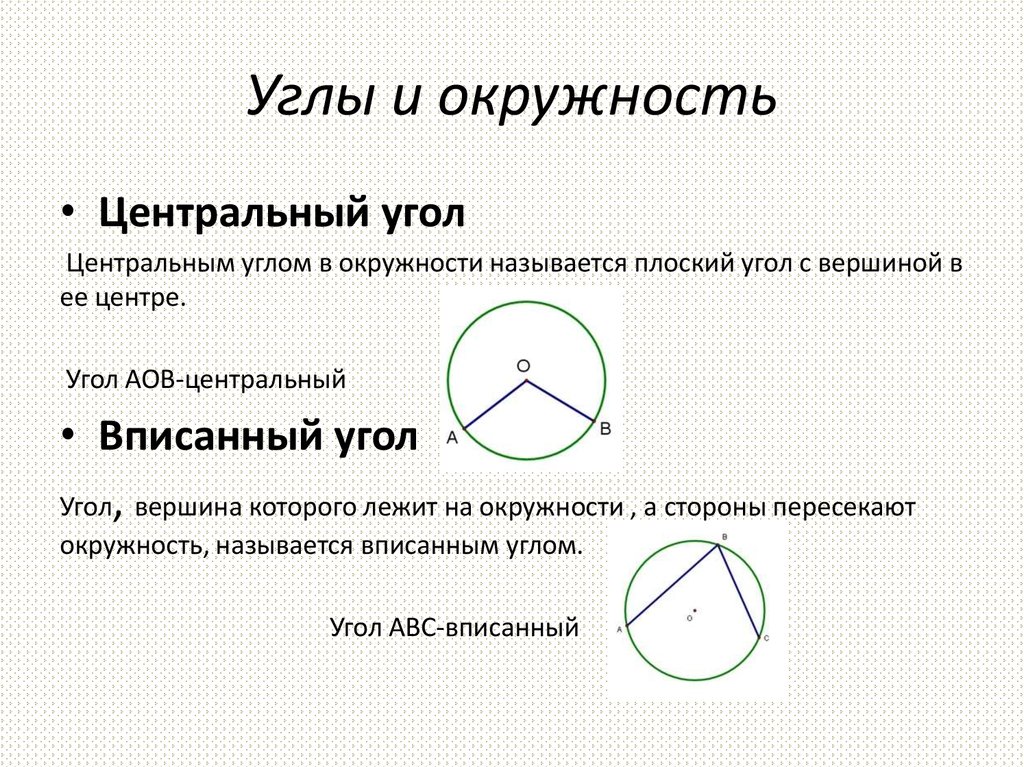
5. Углы и окружность
• Центральный уголЦентральным углом в окружности называется плоский угол с вершиной в
ее центре.
Угол АОВ-центральный
• Вписанный угол
Угол, вершина которого лежит на окружности , а стороны пересекают
окружность, называется вписанным углом.
Угол АВС-вписанный
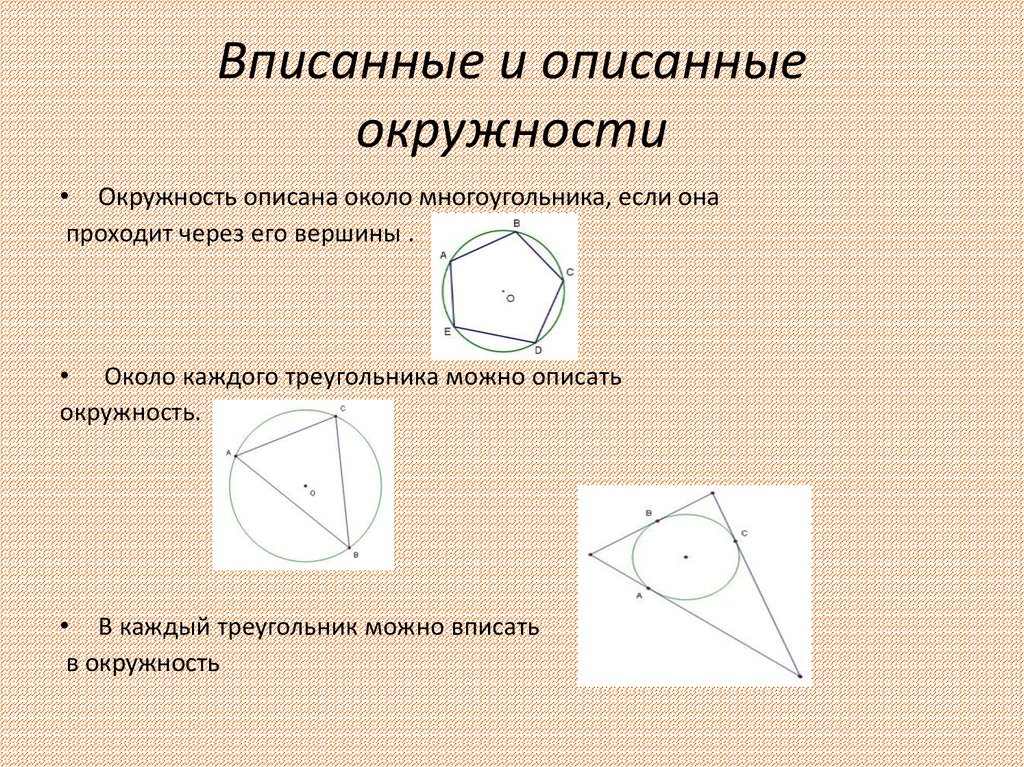
6. Вписанные и описанные окружности
• Окружность описана около многоугольника, если онапроходит через его вершины .
• Около каждого треугольника можно описать
окружность.
• В каждый треугольник можно вписать
в окружность
7. Длины и площади
• Длиныдлина окружности С радиуса R
С=2















 Математика
Математика








