Явление электромагнитной индукции

1.

Явление электромагнитной индукции..
1831 г.

2. Электромагнитная индукция (ЭМИ)

Опыты Фарадея
ЭДС в контуре можно создавать
тремя способами:
1. Двигая контур в магнитном поле.
2. Двигая магнит вблизи провода.
3. Меняя ток в соседнем проводе.

3.

Закон Фарадея (1831)
Независимо от способа изменения потока вектора магнитной индукции Ф,
явление ЭМИ можно описать единым законом.
.
Во всяком замкнутом проводящем контуре при изменении потока магнитной
индукции через поверхность, ограниченную этим контуром, возникает
электрический ток (индукционный ток).
Электродвижущая сила, возникающая при этом, пропорциональна скорости
изменения магнитного потока, сцепленного с этим контуром:
Закон Фарадея в
системе Си
d
Проводящий
контур
I
S
dS
B
n
I
Поверхность
ограниченная
контуром
i
dt
Φ в Веберах
εi в В/м
dΦ=BcosαdS=Bn dS
Ф Bn dS
S
При изменении Ф через поверхность,
ограниченную контуром, в контуре возникает
ЭДС и ток.

4.

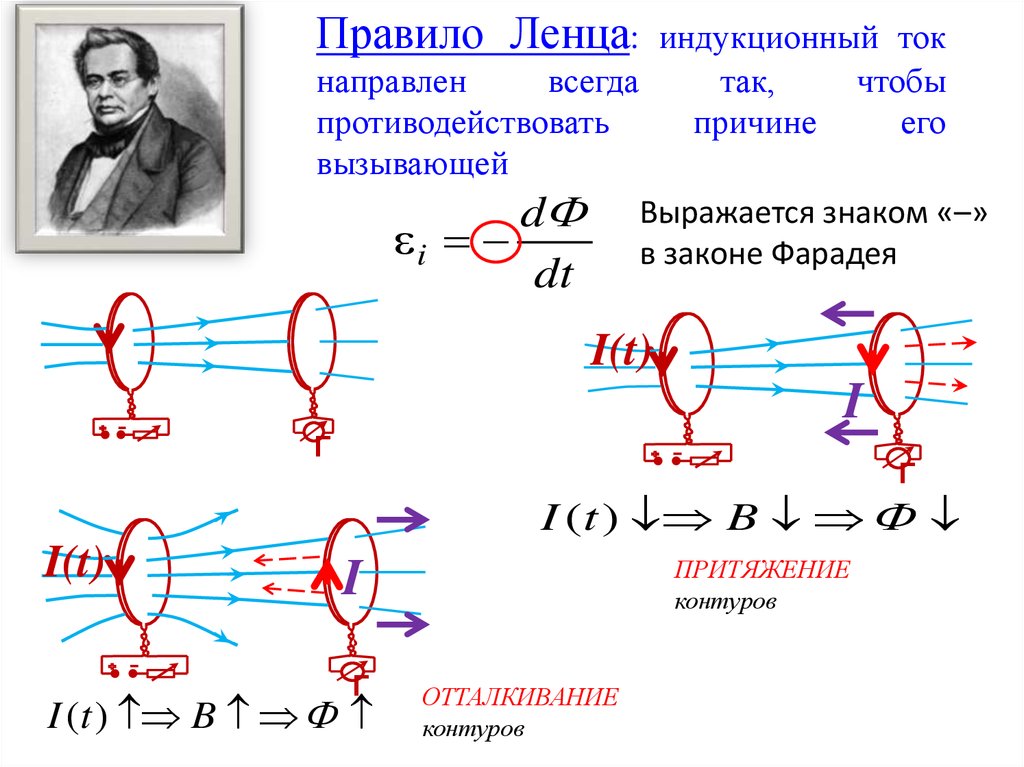
Правило Ленца:
индукционный ток
направлен
всегда
так,
чтобы
противодействовать
причине
его
вызывающей
d Выражается знаком «–»
i
в законе Фарадея
dt
I(t)
I
Г
Г
I (t ) B
I(t)
ПРИТЯЖЕНИЕ
контуров
I
Г
I (t ) B
ОТТАЛКИВАНИЕ
контуров

5.

Вывод закона Фарадея
1. Проводник
контура, движется со
длиной l, являющийся частью замкнутого
скоростью V в однородном магнитном поле. B перпендик. плоскости контура.
I
e
f LII
l
V
На электроны движущегося проводника
действует сила Лоренца
f LII e[v B ]
Это сила не кулоновской природы (сторонняя)
Величина, равная работе сторонних сил по
перемещению заряда на участке цепи, деленной на величину заряда, называется
ЭДС индукции
электродвижущей силой (ЭДС):
12
Aстор
q
ind
eBV l
BV l
e
Знак «-»: εind создаёт ток, направленный
против положительного обхода контура,
определяемого вектором B по правилу правого винта.
ind
dx B dS
d
BVl Bl
dt
dt
dt
ind
dФ
dt

6.

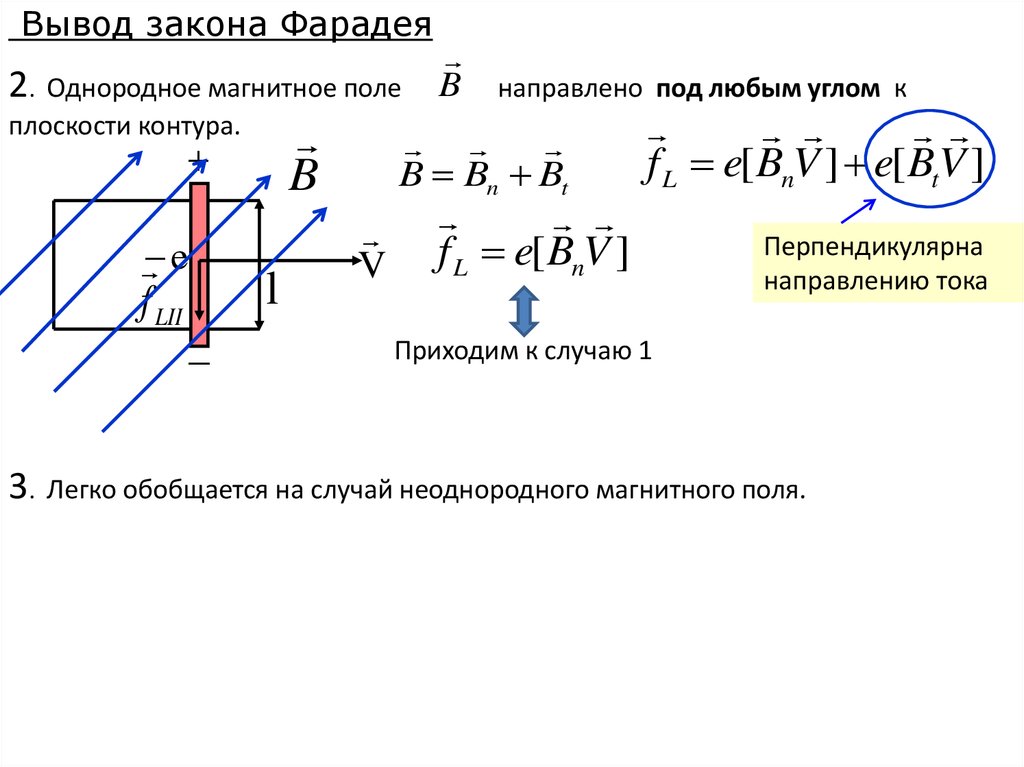
Вывод закона Фарадея
2. Однородное магнитное поле
B
плоскости контура.
e
f LII
l
B
направлено под любым углом к
B Bn Bt
V
f L e[ BnV ] e[ BtV ]
f L e[ BnV ]
Перпендикулярна
направлению тока
Приходим к случаю 1
3. Легко обобщается на случай неоднородного магнитного поля.

7.

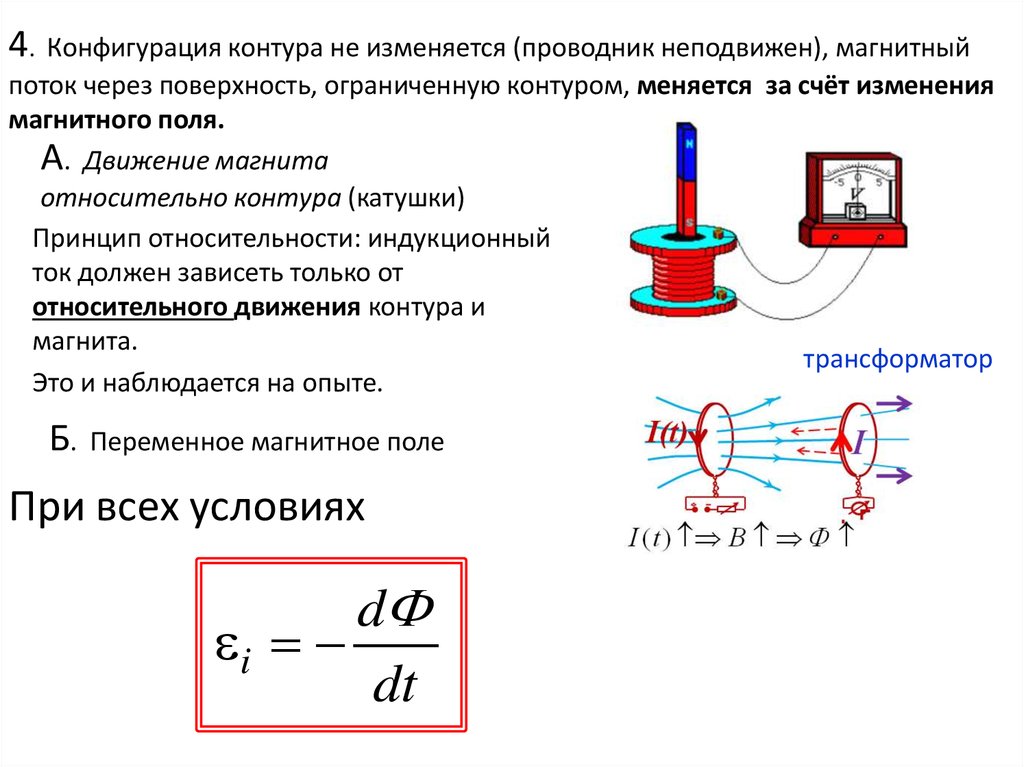
4. Конфигурация контура не изменяется (проводник неподвижен), магнитный
поток через поверхность, ограниченную контуром, меняется за счёт изменения
магнитного поля.
А. Движение магнита
относительно контура (катушки)
Принцип относительности: индукционный
ток должен зависеть только от
относительного движения контура и
магнита.
трансформатор
Это и наблюдается на опыте.
Б.
Переменное магнитное поле
При всех условиях
d
i
dt

8.

Закон Фарадея (1831)
Независимо от способа изменения потока вектора магнитной
индукции Ф, явление ЭМИ можно описать единым законом.
Во всяком замкнутом проводящем контуре при изменении потока магнитной
индукции через поверхность, ограниченную этим контуром, возникает
электрический ток (индукционный ток).
Электродвижущая сила, возникающая при этом, пропорциональна скорости
изменения магнитного потока, сцепленного с этим контуром:
d
i
dt

9.

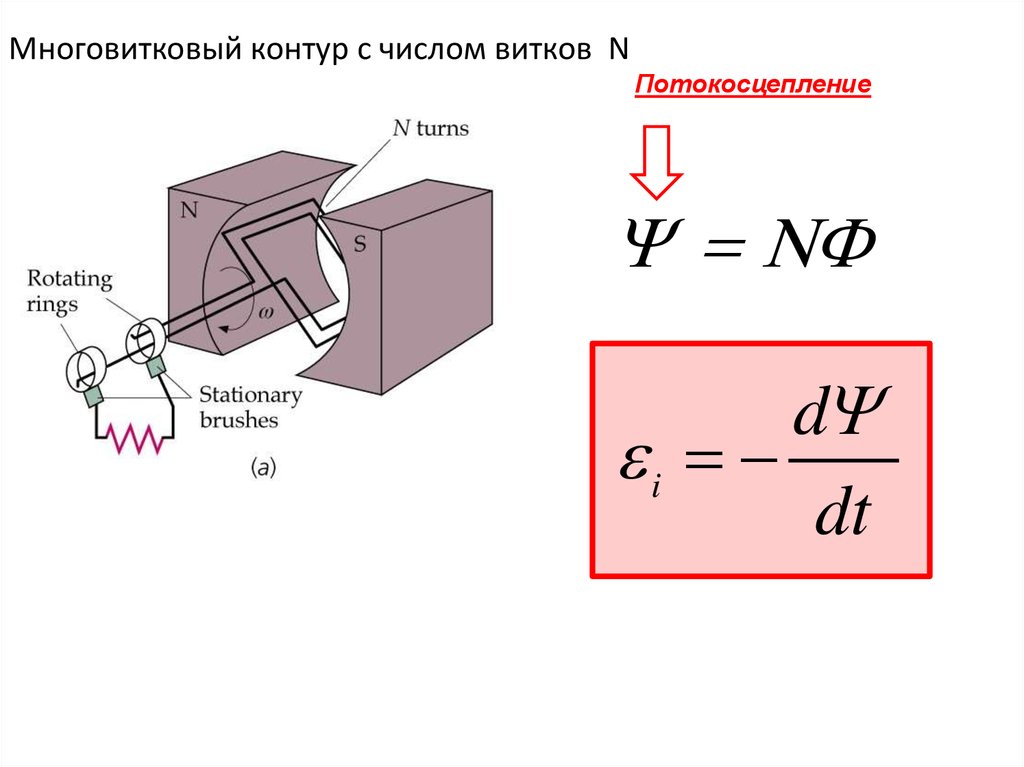
Многовитковый контур с числом витков N
Потокосцепление
d
i
dt

10.

Явление самоиндукции. Индуктивность .
Контур с током создаёт магнитный поток Φ.
d
Если ток меняется во времени I = I(t), то dt 0
В самом контуре возникает ЭДС
I(t)
I
S
d
dt
ЭДС самоиндукции
ЭДС самоиндукции препятствует
изменению тока в контуре:
Если ток возрастает, возникает
индукционный ток, направленный в
противоположную сторону
Если ток убывает, возникает индукционный ток, направленный
в ту же сторону.

11.

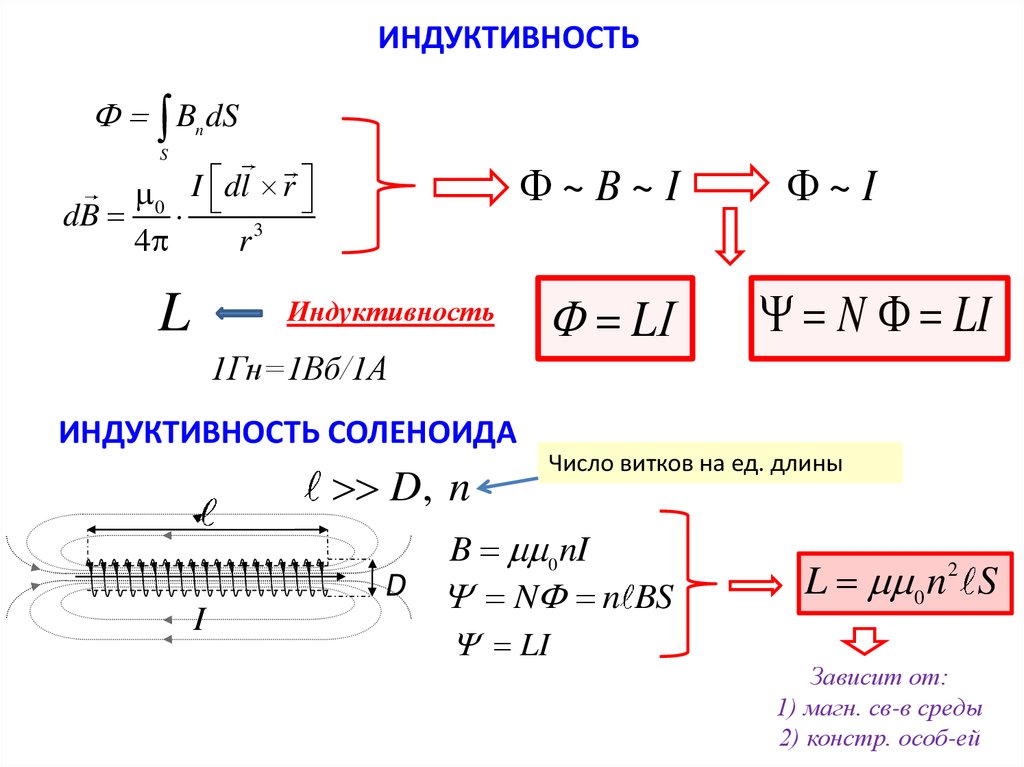
ИНДУКТИВНОСТЬ
Bn dS
S
~B~I
0 I dl r
dB
4
r3
L
Индуктивность
L
~I
N LI
1Гн=1Вб/1А
ИНДУКТИВНОСТЬ СОЛЕНОИДА
D, n
I
Число витков на ед. длины
B 0 nI
D N n BS
LI
L 0 n 2 S
Зависит от:
1) магн. св-в среды
2) констр. особ-ей

12.

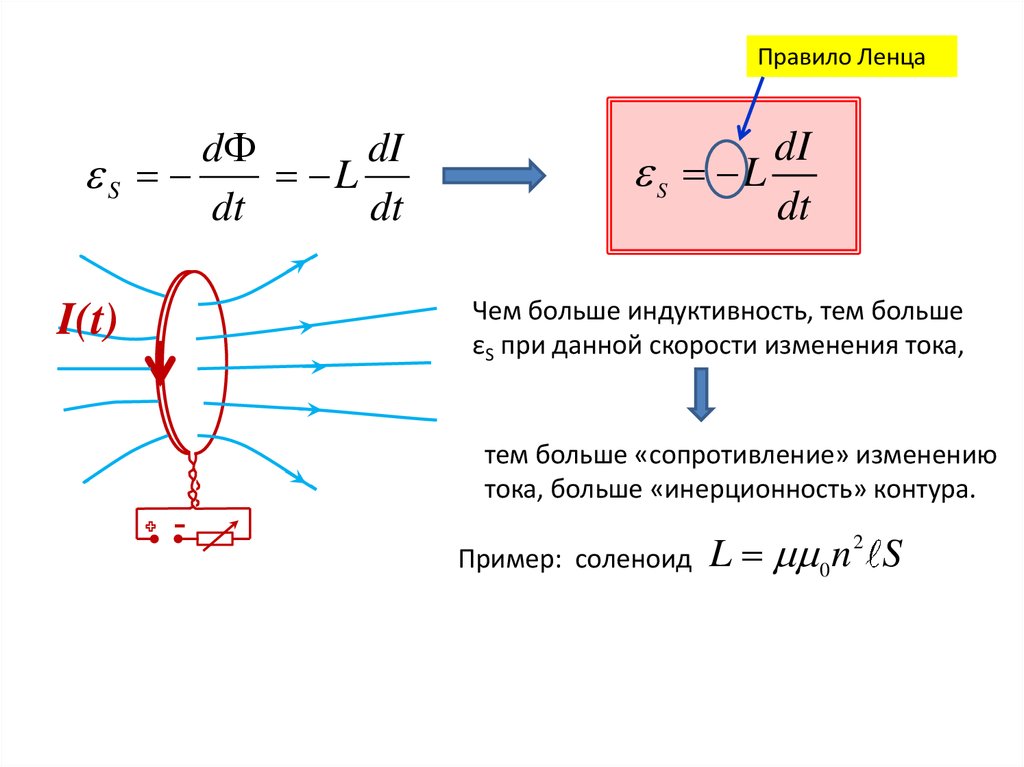
Правило Ленца
d
dI
S
L
dt
dt
I(t)
dI
S L
dt
Чем больше индуктивность, тем больше
εS при данной скорости изменения тока,
тем больше «сопротивление» изменению
тока, больше «инерционность» контура.
Пример: соленоид
L 0 n 2 S

13.

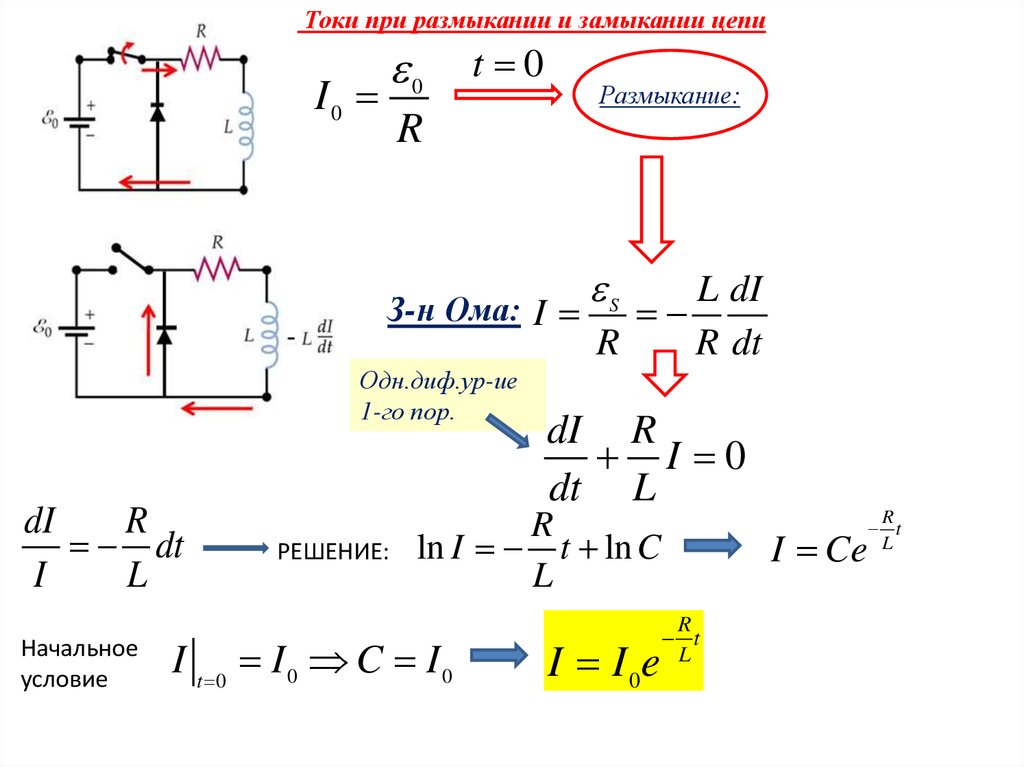
Токи при размыкании и замыкании цепи
0
I0
t 0
Размыкание:
R
З-н Ома: I
Одн.диф.ур-ие
1-го пор.
dI
R
dt
I
L
Начальное
условие
РЕШЕНИЕ:
S
L dI
R
R dt
dI R
I 0
dt L
R
ln I t ln C
L
I t 0 I 0 C I 0
I I 0e
I Ce
R
t
L
R
t
L

14.

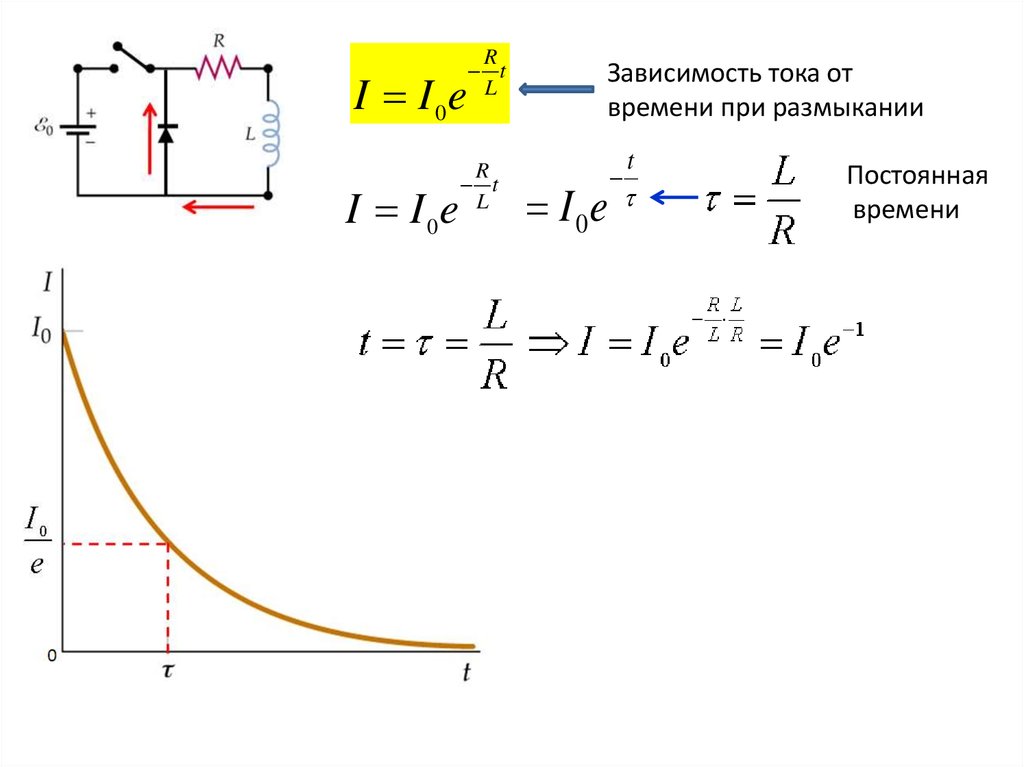
I I 0e
I I 0e
R
t
L
R
t
L
Зависимость тока от
времени при размыкании
I 0e
t
Постоянная
времени

15.

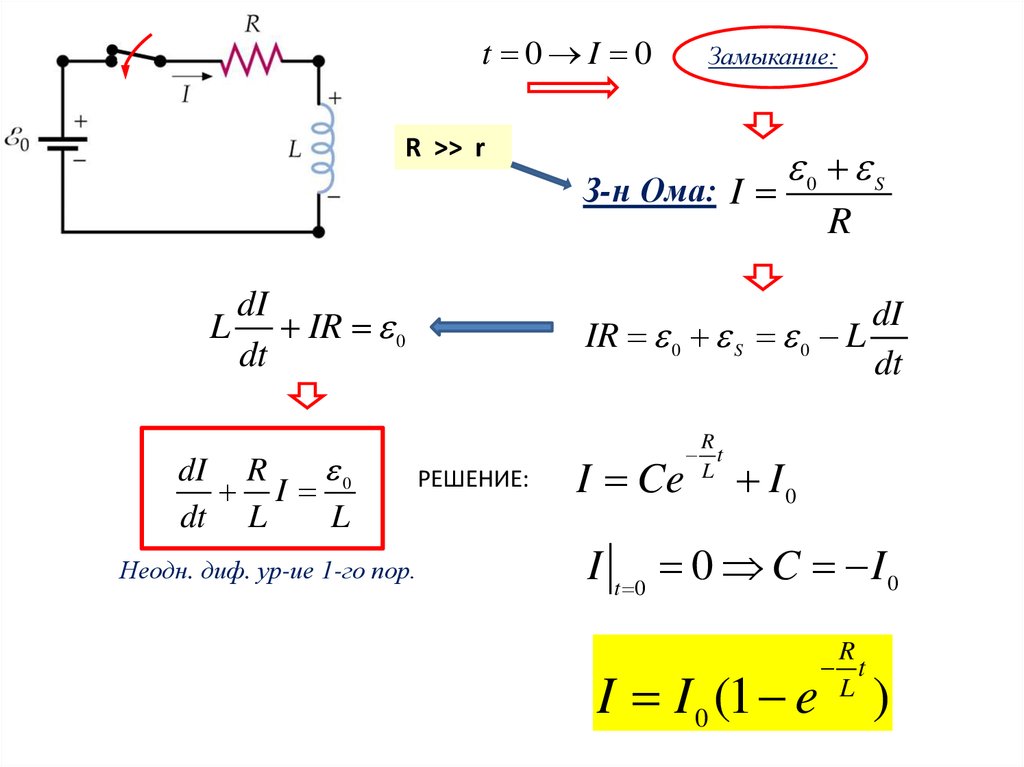
t 0 I 0
Замыкание:
R >> r
З-н Ома: I
dI
L IR 0
dt
0
dI R
I
dt L
L
Неодн. диф. ур-ие 1-го пор.
0 S
R
dI
IR 0 S 0 L
dt
РЕШЕНИЕ:
I Ce
R
t
L
I0
I t 0 0 C I 0
I I 0 (1 e
R
t
L
)

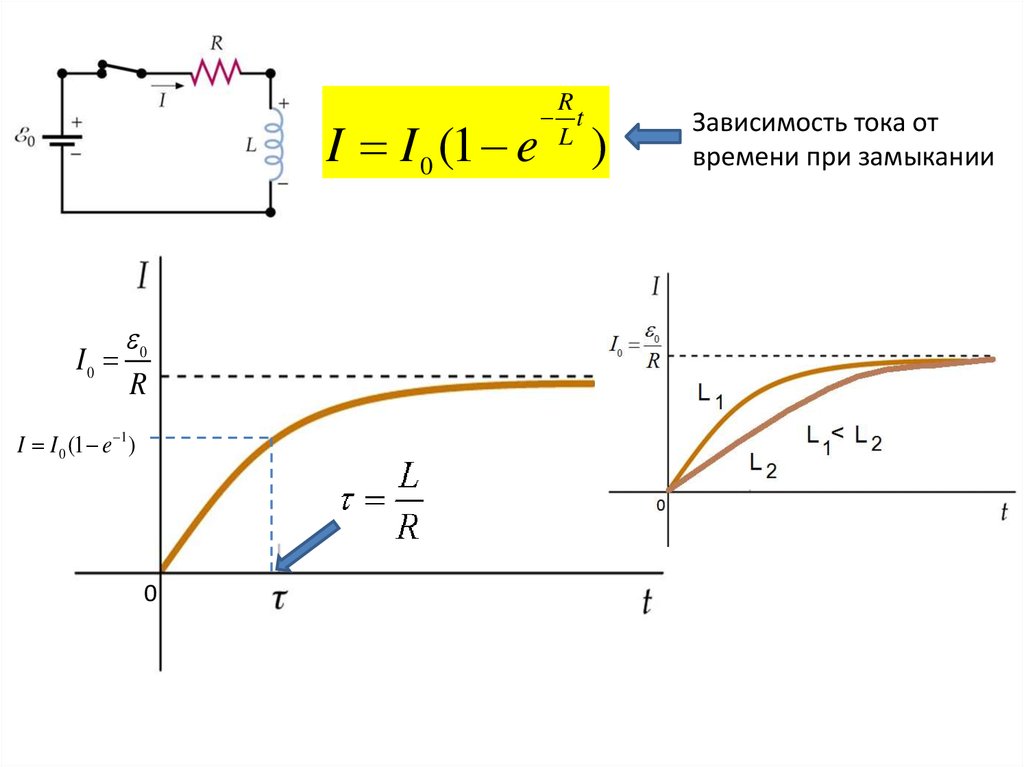
16.

I I 0 (1 e
I0
0
R
I I 0 (1 e 1 )
0
R
t
L
)
Зависимость тока от
времени при замыкании