Цепи синусоидального тока. (Лекция 3)

1.

ВУНЦ ВВС «ВВА» (филиал, г. Краснодар)
Кафедра физики и электротехники
Учебная дисциплина
Электротехника и электроника
Тема 2/1
Цепи синусоидального тока
Лекция № 3

2.

Учебные вопросы:
1. Электрические цепи при гармоническом воздействии.
Гармонические колебания. Основные понятия и
определения. Действующее и среднее значения
гармонической функции
2. Способы представления гармонических колебаний
3. Гармонические колебания в пассивных элементах
электрической цепи. Методы анализа линейных
электрических цепей с двуполюсными элементами
4*. Мощность электрической цепи переменного тока
Литература:
Бухонский М.И., Найдёнов С.В., Тельнов Г.В. Электротехника и электроника.
Аналоговая схемотехника. Часть 1: Учебное пособие.– Краснодар: Филиал
ВУНЦ ВВС «ВВА имени проф. Н.Е.Жуковского и Ю.А.Гагарина» (г. Краснодар),
2011.– с. 53-71.

3.

1. Электрические цепи при гармоническом воздействии. Гармонические колебания. Основные
понятия и определения. Действующее и среднее значения гармонической функции
Сигналы - физические процессы, параметры которых содержат информацию:
используются постоянные токи (напряжения), их колебания или импульсы, которые
рассматриваются как носители информации
Сигналы
Детерминированные
Р(t)=1, P(t)-const
Случайные
P(t) 1, P(t)=f(t)
Периодические
Непериодические
Простые
Сложные
Постоянного
тока
Гармонические
Периодические
Непериодические
Квазинепрерывные
Импульсные
Видеоимпульсы
Радиоимпульсы

4.

Гармонические колебания широко используются в электротехнике и
электронике для передачи электрической энергии и сигналов, а также могут
применяться в качестве простейшего испытательного сигнала.
Гармоническим колебанием называют колебания, изменяющиеся по закону
синуса или косинуса. Далее рассматривается только синусоидальный закон
i(t ) I m sin( t i )
Амплитуда i(t)
i(t)
u>0
u(t ) U m sin( t u )
Т
u(t)
2Т
3Т
Параметры гармонических колебаний
Im,Um – амплитуда тока или напряжения (Im,Um ) = const
( t+ I),( t+ u) – полная фаза (фазовый угол), фаза, рад
d ( t u )
dt
2
Угловая частота, рад/с.
Т
t
1
f , Гц
Т
2 f

5.

При совместном рассмотрении двух гармонических колебаний одинаковой
частоты разность их фаз, равную разности их начальных фаз обычно называют
сдвигом фаз и обозначают или .
u(t ) U m sin( t u )
i(t ) I m sin( t i )
u i
0
Колебания синфазные (совпадают по фазе)
Колебания противофазные
Колебания находятся в квадратуре
2
0, т.е. u i
Напряжение отстает от тока по фазе
Напряжение опережает ток по фазе
0, т.е. u i
Для питания различных электроэнергетических установок в России принята
промышленная частота f = 50 Гц. В качестве источников гармонических колебаний
промышленной частоты используются электромашинные генераторы
f p p n / 60
где pp число пар полюсов ротора, n – (об.мин) –
скорость вращения ротора.

6.

В практической электротехнике для оценки прежде всего
энергетических возможностей переменного тока вводятся понятия
действующего (среднеквадратического) и среднего значения
переменного тока за период.
Определение 1. Действующим (его также называют
эффективным
или
среднеквадратическим)
значением
периодического тока i(t) называют такой постоянный ток I,
который в одном и том же сопротивлении R за время одного
периода Т тока i(t) выделяет равное с переменным током
количества тепла
Em
Im
Um
I
U 0,707U m E
I 0,707 I m U
2
2
2
Определение 2. Средним значением IСР периодического тока
i(t) называют среднее значение тока за положительный
полупериод, совпадающее со средним значением по модулю.
I CP 0,637 I m
U CP 0,637 U m
ECP 0,637 Em

7.

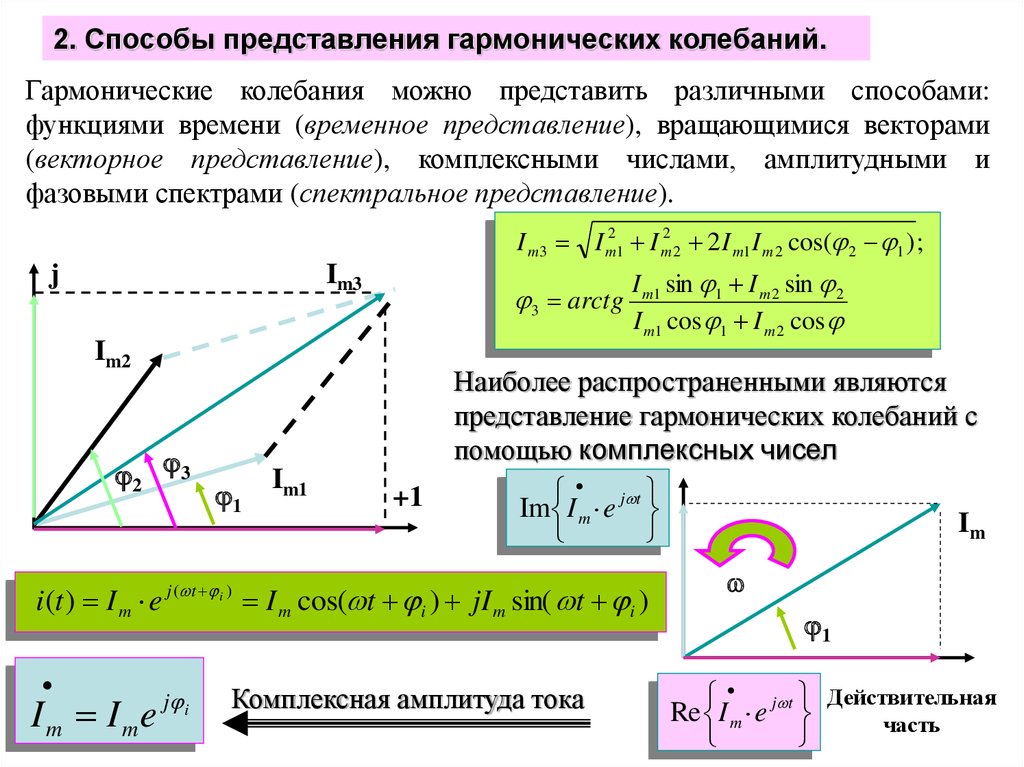
2. Способы представления гармонических колебаний.
Гармонические колебания можно представить различными способами:
функциями времени (временное представление), вращающимися векторами
(векторное представление), комплексными числами, амплитудными и
фазовыми спектрами (спектральное представление).
I m 3 I m21 I m2 2 2 I m1 I m 2 cos( 2 1 ) ;
j
Im3
3 arctg
Im2
2 3
i (t ) I m e
I m I me
1
j ( t i )
j i
Im1
+1
I m1 sin 1 I m 2 sin 2
I m1 cos 1 I m 2 cos
Наиболее распространенными являются
представление гармонических колебаний с
помощью комплексных чисел
j t
Im I m e
Im
I m cos( t i ) jI m sin( t i )
Комплексная амплитуда тока
1
j t Действительная
Re I m e
часть

8.

Тригонометрическая форма записи комплексных чисел
U x jy r cos( ) j sin( )
y r sin( )
x r cos( )
Показательная (экспоненциальная) форма записи комплексных чисел
j
U a jb r e r exp( j )
arctg
r a jb 0
2
u(t ) U m cos( t ) jUm sin( t ) U me
2
j ( t )
U
j t
U me e
j
b
a
U m e j t
U m U m j
e U e j
2
2
Комплексное действующее
значение
Комплексная форма записи законов Ома и Кирхгофа
Im
Um
Z
;I
U
Z
n
I
k 1
mk
0
n
I
k 1
k
0
n
Z
k 1
k
n
I k Ek
k 1

9.

Пример: Комплексная амплитуда напряжения
U m 100 jВ,
100
частота f = 1кГц. Записать выражение для мгновенного
напряжения.
Решение. Угловая частота
рад/с,
амплитуда
2 f 2 103 6280
U m ( 100) 2 100 2 100 2 B;
tg = 100/(-100) = - 1; т. к. действительная часть комплексной
амплитуды отрицательная, а мнимая часть положительная, то
вектор во второй четверти и, следовательно, =3 /4.
Таким образом, мгновенное значение напряжения
u (t ) 100 2 sin( 6280t 3 / 4) В.

10.

3. Гармонические колебания в пассивных элементах электрической цепи.
i(t)
3.1 Резистивный элемент и его характеристики
R
Пусть через резистор протекает ток i(t):
i (t ) I m sin( t i ) I m e
uR(t)
j ( t i )
I m e j t
u(t ) R i(t ) R I m sin( t i ) U mR sin( t i ) U mR sin( t u )
u (t ) R I m e
j t
U mR e
j t
j i
U mR e e
j t
U mR e
j u
e
j t
комплексная
форма записи
Мгновенная мощность колебания в резисторе
j
R 0
Im
p(t ) u i RI m sin( t i ) I m sin( t i )
Um
RI m2 sin 2 ( t i ) U mR I m sin 2 ( t i )
2U mR I m 2
sin ( t i ) 2U R I sin 2 ( t i )
2 2
+1
Колебания синфазные U I 1 cos 2( t ) 0
R
i
u= i
U mR R I m U R I
R

11.

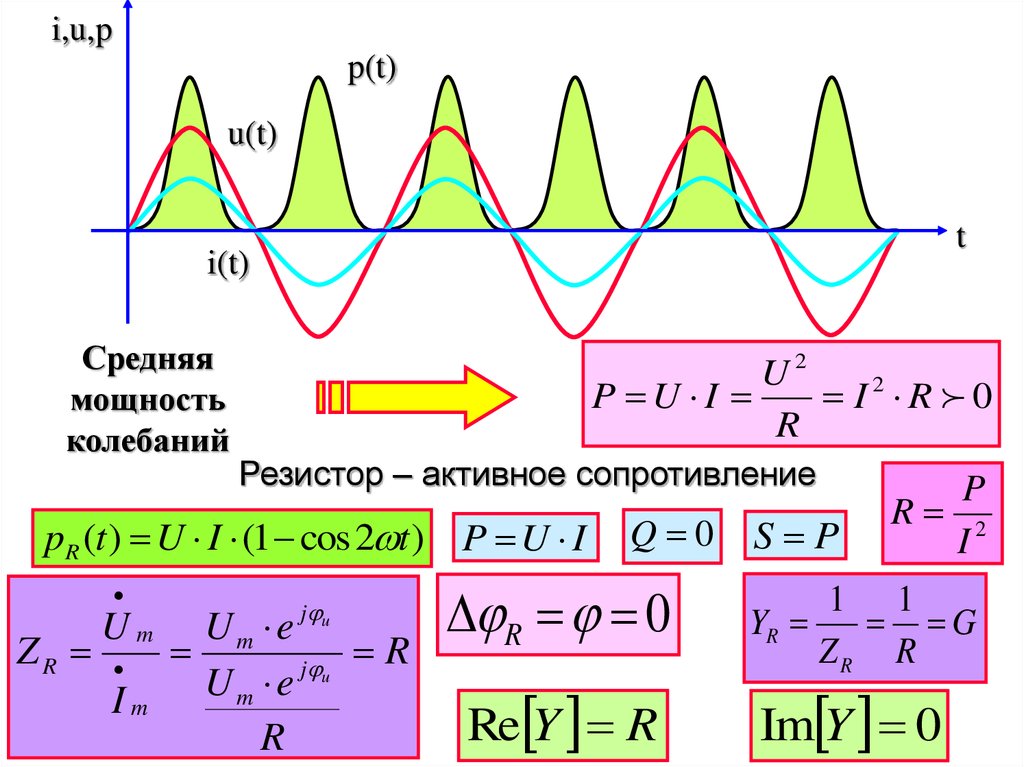
i,u,p
p(t)
u(t)
t
i(t)
Средняя
мощность
колебаний
U2
P U I
I2 R 0
R
Резистор – активное сопротивление
pR (t ) U I (1 cos 2 t ) P U I
ZR
Um
Im
j u
Um e
R
j u
Um e
R
Q 0
R 0
Re Y R
S P
P
R 2
I
1 1
YR
G
ZR R
Im Y 0

12.

3.2 Индуктивный элемент и его характеристики
L
d ( I m sin( t i ))
di
uL L L
L I m cos( t i )
i
dt
dt
uL(t)
U mL cos( t i ) U mL sin( t i ) U mL sin( t u )
i(t ) I m sin( t i )
2
u i ; u i
2
2
ZL
U mL
Im
j ( i 90 )
L Im e
I m e j
i
U mL L I m
L e
j 90
j L
X L ( ) L
Комплексное
сопротивление
L -элемента
Z L ( j ) j L j X L Re Z L 0 Im Z L L X L
Комплексная проводимость L -элемента
1
1
1
YL
j
Re YL 0
j
L
L
ZL
1
Im YL
bL
L

13.

Напряжение на индуктивности
имеет форму гармонического
колебания и опережает по фазе
колебания тока на угол + /2.
Колебания тока и напряжения
находятся в квадратуре
j
Um
u
Im
i
+1
Мгновенная мощность изменяется во времени
pL u L i U m sin( t i ) I m sin( t i )
2
1
1
I mU m cos( t i t i ) I mU m cos( t i t i )
2
2 2
2
1
1
I mU m cos( 2 t 2 i ) I mU m sin( 2 t 2 i ) IU sin 2( t i )
2
2 2
по синусоидальному закону с частотой в два раза большей частоты тока
Мгновенная мощность положительна при нарастании по абсолютному
значению тока в индуктивном элементе 0<t<Т/4 (накопление энергии в
магнитном поле катушки индуктивности).

14.

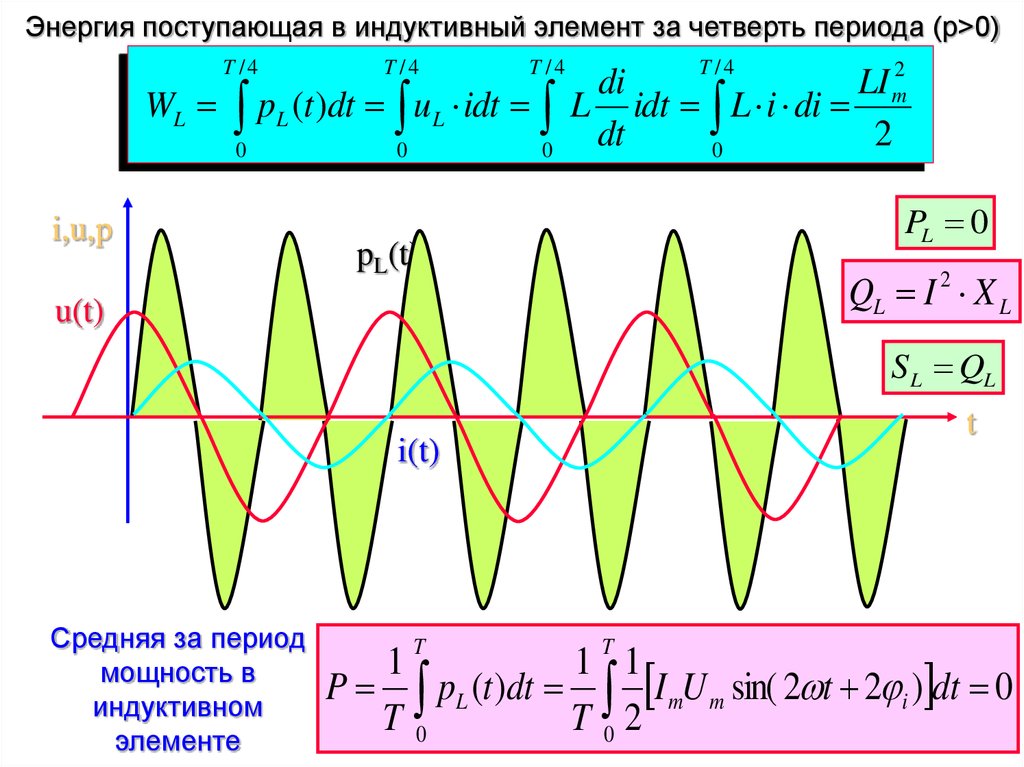
Энергия поступающая в индуктивный элемент за четверть периода (р>0)
T /4
WL
T /4
p (t )dt u
L
0
i,u,p
T /4
L
0
idt
0
T /4
LI m2
di
L idt L i di
dt
2
0
PL 0
pL(t)
QL I 2 X L
u(t)
S L QL
t
i(t)
Средняя за период
мощность в
индуктивном
элементе
T
T
1
1 1
P pL (t )dt I mU m sin( 2 t 2 i ) dt 0
T0
T 02

15.

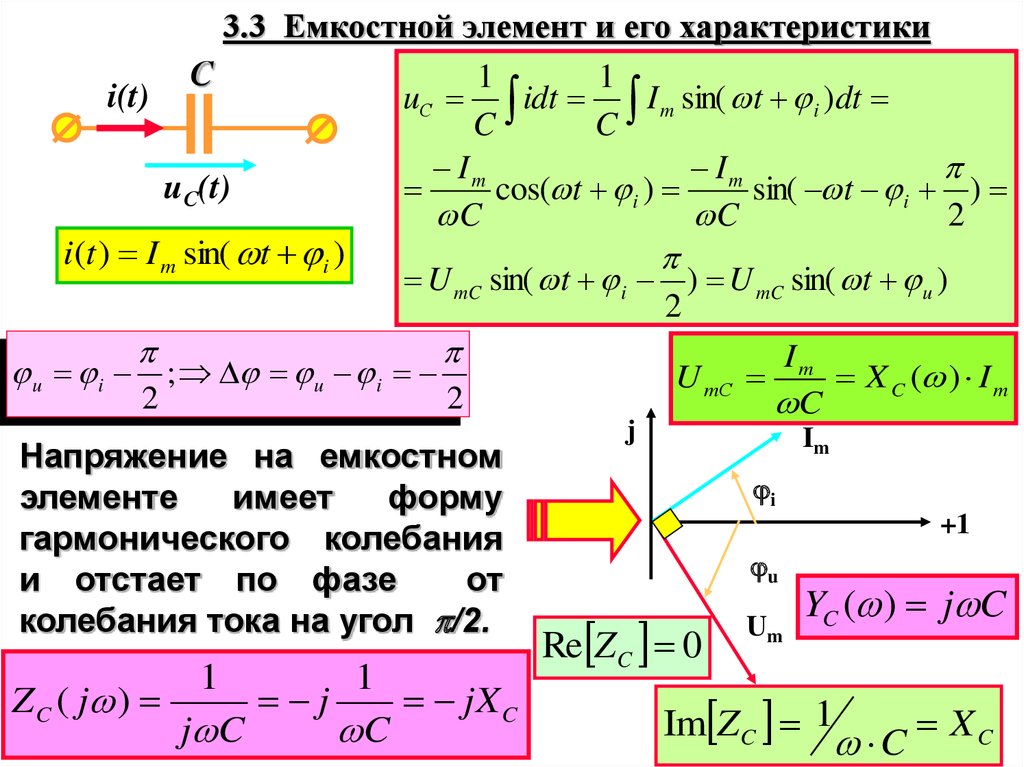
3.3 Емкостной элемент и его характеристики
С
1
1
i(t)
uС idt I m sin( t i )dt
C
C
Im
Im
uС(t)
cos( t i )
sin( t i )
C
C
2
i(t ) I m sin( t i )
U mC sin( t i ) U mC sin( t u )
2
Im
u i ; u i
U mС
X C ( ) I m
2
2
C
Напряжение на емкостном
элементе
имеет
форму
гармонического колебания
и отстает по фазе
от
колебания тока на угол /2.
1
1
Z C ( j )
j
jX C
j C
C
j
Im
i
+1
u
Re Z C 0
Um
YC ( ) j C
Im Z C 1
C XC

16.

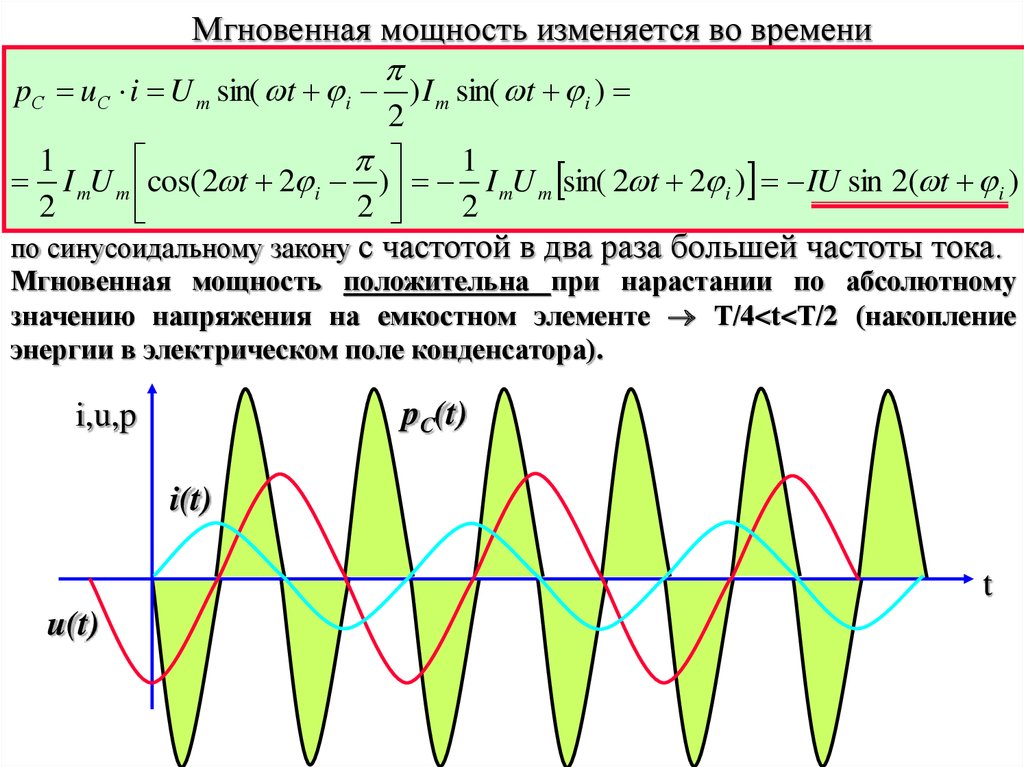
Мгновенная мощность изменяется во времени
pС uС i U m sin( t i ) I m sin( t i )
2
1
1
I mU m cos( 2 t 2 i ) I mU m sin( 2 t 2 i ) IU sin 2( t i )
2
2
2
по синусоидальному закону с частотой в два раза большей частоты тока.
Мгновенная мощность положительна при нарастании по абсолютному
значению напряжения на емкостном элементе Т/4<t<Т/2 (накопление
энергии в электрическом поле конденсатора).
pС(t)
i,u,p
i(t)
t
u(t)

17.

Энергия поступающая в емкостной элемент за четверть периода
(рС > 0)
T /2
WС
p
Т
L
T /2
T /2
Т
Т
(t )dt uС idt
4
4
4
Um
CU m2
du
СU m
dt C U m du
dt
2
0
T
T
Средняя за период
1
1
1
P pС (t )dt I mU m sin( 2 t 2 i ) dt 0
мощность в
T0
T0 2
емкостном элементе
В чисто емкостной цепи, как и в чисто индуктивной цепи
потери энергии отсутствуют. Вначале происходит заряд
конденсатора, энергия при этом накапливается в
электрическом поле конденсатора. Затем происходит
разряд конденсатора, энергия, запасенная в электрическом
поле, поступает к источнику.
PC 0
QC U I I 2 X L
S L QL

18.

Зависимость сопротивлений пассивных элементов
электрической цепи от частоты переменного тока
i(t)
R
L
i
X L L X L ( )
uR(t)
R
uL(t)
XL
при L1
R2 > R1
при R2
L1 > L2
при L2
при R1
ω
i(t)
С
ω
XC
C1 > C2
uС(t)
1
XC
X C ( )
C
при C2
при C1
ω

19.

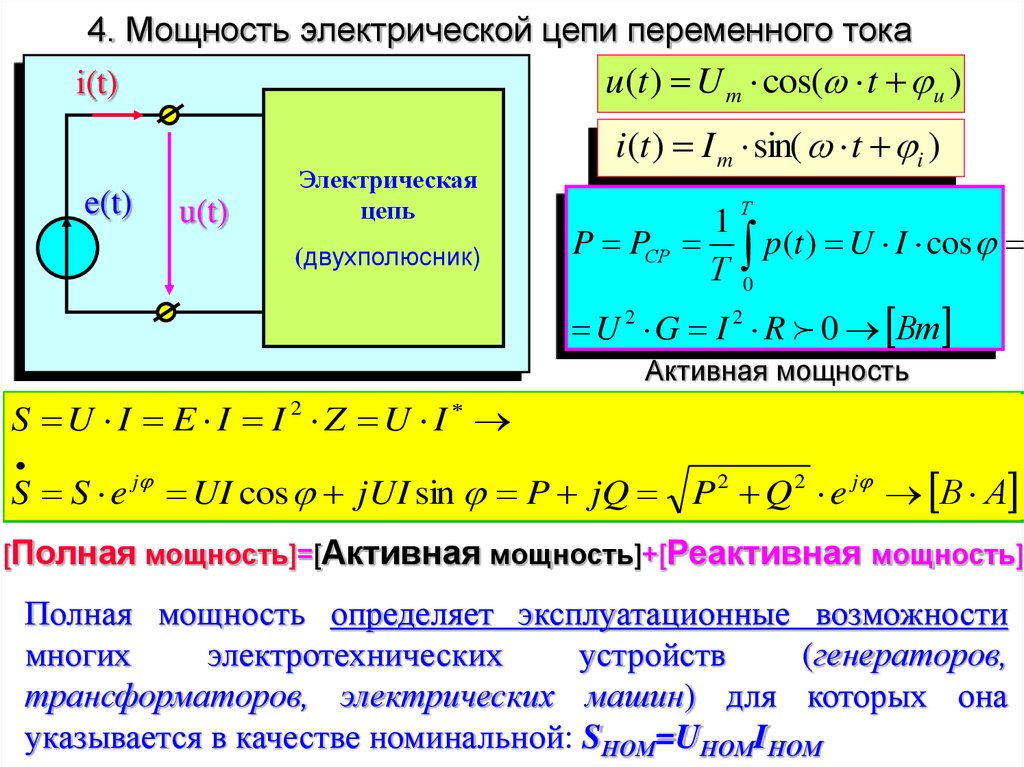
4. Мощность электрической цепи переменного тока
u(t ) U m cos( t u )
i(t)
e(t)
u(t)
Электрическая
цепь
(двухполюсник)
i(t ) I m sin( t i )
Т
1
P PСР p(t ) U I cos
Т0
U 2 G I 2 R 0 Вт
Активная мощность
S U I E I I2 Z U I
S S e j UI cos jUI sin P jQ P 2 Q 2 e j В А
[Полная мощность]=[Активная мощность]+[Реактивная мощность]
Полная мощность определяет эксплуатационные возможности
многих
электротехнических
устройств
(генераторов,
трансформаторов, электрических машин) для которых она
указывается в качестве номинальной: SНОМ=UНОМIНОМ

20.

Реактивная мощность может быть как положительной, так и отрицательной
Если электрическая цепь имеет индуктивный характер, > 0 и
PQ > 0, если – емкостной характер, то < 0 и PQ < 0.
P
cos
S
P
P
P2 Q2 U I
S P jQ
S
Q P U I cos
Р
Q U I sin
Коэффициент мощности
Чем больше cos , тем больше степень использования
P
полной мощности, тем меньшим током при заданном I
U cos
напряжении можно доставить к потребителю активную
мощность
От значения I сечения подводящих энергию проводов, кабелей, линий
передач. Потери энергии в подводящих проводах пропорциональны I2
PПОТ I 2 RПОТ
(ток) ( cos )
Для увеличения cos необходимо уменьшать реактивную мощность.
При Q = 0 имеем cos = 1. Так как QL > 0 , а QС < 0, то для компенсации
реактивной мощности параллельно нагрузке, имеющей как правило,
индуктивный характер, подключают компенсирующую емкость, значение
которой выбирают из условия: Q = QL + QС = 0, т.е. QL = - QС

21.

Общие выводы
1. В режиме холостого хода, т.е. при
RH = ∞ (разомкнутая электрическая
цепь)
2. В режиме короткого замыкания,
т.е. при RH = 0 (короткозамкнутая
электрическая цепь)
3. В согласованном режиме работы
RИ = RH
XX
RH
1
RИ RH
КЗ
RH
0
RИ RH
CP 0,5
В случае, когда необходимо обеспечить
максимальную мощность независимо от экономических
затрат (значения КПД) источники работают в
согласованном режиме (устройства автоматики –
мощности управляющих сигналов малы)
Для силовых установок (RH >> RИ) режим близкий
к режиму холостого хода важен КПД