Похожие презентации:
Формулы косинуса суммы и разности двух аргументов
1.
2.
yПовернём
C(x ;y )
радиус ОА,
равный 1, на
угол
x и на угол
A(x;y)
2
B(x1;y1)
O
2
3.
yC(x2;y2)
B(x1;y1)
O
x
OB x1 ; y1
OC x2 ; y2
Найдём скалярное произведение
векторов ОВ и ОС.
OB OC x1 x2 y1 y2
OB OC OB OC cos BOC cos BOC
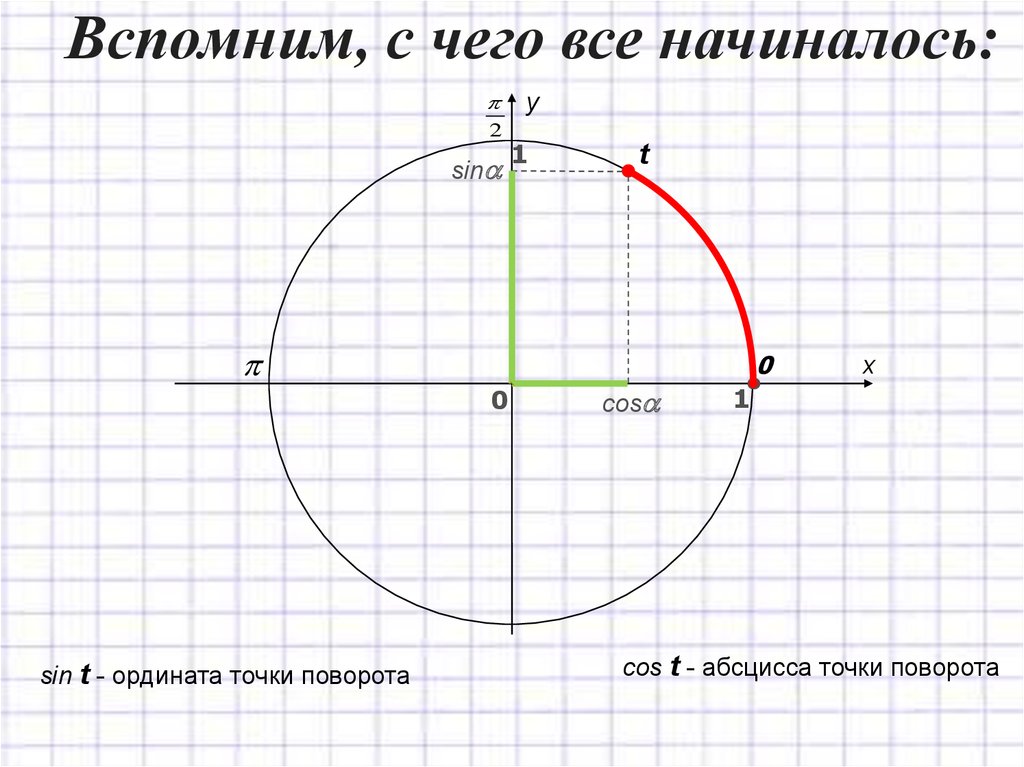
4. Вспомним, с чего все начиналось:
2sin
1
t
0
0
sin t - ордината точки поворота
y
cos
x
1
cos t - абсцисса точки поворота
5.
yC(x2;y2)
B(x1;y1)
O
OB OC x1 x2 y1 y2
(1)
x
Из определения синуса и косинуса:
x1 cos
y1 sin
x2 R cos
y2 R sin
Подставим данные значения в правую часть равенства (1):
OB OC cos cos sin sin
6.
yy
C(x2;y2)
B(x1;y1)
x
C(x2;y2)
B(x1;y1)
O
O
BOC
BOC 2 ( )
В любом случае:
cos BOC
x
7.
OB OC cos( )OB OC cos cos sin sin
Левые части равенств равны, значит правые тоже равны.
Получаем формулу косинуса разности двух аргументов:
cos( ) cos cos sin sin
Формула косинуса суммы двух аргументов:
cos( ) cos( ( )) cos cos( ) sin sin( )
cos( ) cos cos sin sin
8. 1. Вычислить: cos 750
Воспользуемся тем, что 750 = 450 + 300;cos750 = cos ( 450 + 300) =
cos450·cos300 – sin450·sin300=
cos( ) cos cos sin sin
9. 2. Вычислить: cos150
Воспользуемся тем, что 150 = 450 - 300;cos150 = cos( 450 - 300) =
cos450·cos300 + sin450·sin300=
cos( ) cos cos sin sin
10. 3. Вычислить:
1) cos370cos80 – sin370sin80;2) cos1070cos170 + sin1070sin170
Ответ: 1)
2) 0
11.
12. cos(x–y)=cosx·cosy +sinx·siny
Докажите следствие:cos( 2 – )=sin
cos(x–y)=cosx·cosy +sinx·siny
0
cos
2
sin
сos( 2 – )=cos 2 ·cos +sin
cos(
2
2
1
2 ·sin
– )= 0∙cosα +1∙sin = sin
13. Синус суммы
sin( ) ?sin( ) cos( ( ))
2
cos(( ) )
2
14.
cos(( ) )2
y
x
cos(x–y)=cosx·cosy +sinx·siny
cos( ) cos sin( ) sin
sin
2
2
cos
sin cos cos sin
sin(α+β)=sin α ·cosβ +cos α ·sinβ
15. Синус разности
sin(α+β)=sin α ·cosβ +cos α ·sinβsin(α+(-β)=
sin α ·cos(-β) +cos α ·sin(-β)
sin(α-β)=sin α ·cosβ -cos α ·sinβ
16.
Формулы сложенияcos( + )=cos ·cos -sin ·sin
cos( – )=cos ·cos +sin ·sin
sin( + )=sin ·cos +cos ·sin
sin( – )=sin ·cos –cos ·sin
17.
Тангенс суммы и разностидвух углов
tg tg
tg
1 tg tg
tg tg
tg
1 tg tg
18.
Котангенс суммы иразности двух углов
сtg сtg 1
сtg
сtg сtg
сtg сtg 1
сtg
сtg сtg
19.
/ / / / // /tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
cos
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
20.
/ / / / // /tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
sin
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
21.
/ / / / // /tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
cos
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
22.
/ / / / // /tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
tg
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
23.
/ / / / // /tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
ctg
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
24. Не бойтесь формул! Учитесь владеть этим инструментом Человеческого гения! В формулах заключено величие и могущество
Человеческого разума!Андрей Андреевич Марков, выдающийся русский математик,
представитель петербургской математической школы,
специалист по теории чисел, теории вероятностей и
математическому анализу.























 Математика
Математика








