Похожие презентации:
Физико-математические основы РКТ
1. НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ» КАФЕДРА «МЕДИЦИНСКАЯ ФИЗИКА» Курс «ФИЗИКА ВИЗУАЛИЗАЦИИ ИЗОБРАЖЕНИЙ В
МЕДИЦИНЕ»доцент каф. 35, к.ф.-м.н. Штоцкий Ю.В.
2. Содержание
Закон БераОсновная задача РКТ
Интегральное (прямое) преобразование Радона
Методы обращения интегрального преобразования
Радона:
1. Метод двумерной фильтрации
2. Метод Фурье-синтеза
3. Метод одномерной фильтрации
3.
Закон Бераy
y
x cos sin
( x, y )
( , )
y sin cos
0
x
хcos уsin
xsin ycos
x
Известно, что всякая прямая может быть описана уравнением:
xcosΘ + ysinΘ – s = 0
где: s - расстояние от начала координат до этой прямой;
Θ - угол, образованный с осью перпендикуляром,
опущенным из начала координат на эту прямую.
Произвольная прямая L однозначно задается двумя параметрами s и Θ.
4. Преобразование Радона
RI( , ) I0exp(- [ , ]d )
R
I ( , )
exp( [ , ]d
I0
R
R
p( , ) ln[ I ( , ) / I0 ]
[ , ]d
Преобразование
Радона
5.
Интегральное преобразование РадонаИнтенсивность излучения, прошедшего сквозь объект
Проекцией p(ξ,θ) называется следующее соотношение:
Подставляя µθ(ξ,ζ) получим интегральное преобразование
Радона для двумерной функции µ(x,y):
(1.7)
Используя свойства δ-функции Дирака преобразование
Радона можно представить в виде:
(1.8)
6.
Пример №1. Вычислим радоновский образ двухраспределений Гаусса
Используя выражение (1.7) получим интегральное преобразование
Радона R(s,φ) для двумерной функции f(x,y):
f(x,y)
R(s,φ)
7.
Основная задача РКТВосстановление неизвестной (искомой) функции µ(x,y)
по измеренному набору проекций p(ξ,θ), связанных с
искомой функцией
интегральным преобразованием Радона (1.7, 1.8).
С математической точки зрения необходимо указать метод
обращения интегрального преобразования Радона.
8.
Обратное преобразование РадонаВ фигурных скобках представлен несобственный интеграл по ξ,
являющийся преобразованием Гильберта (Н)
Интегрирование по углу θ называется обратным проецированием.
Чтобы найти функцию µ(x,y) необходимо:
- продифференцировать по ξ измеренные проекции;
- вычислить гильберт-образы полученных производных;
- провести обратное проецирование.
9.
Недостаткиобратного преобразования Радона
Формула обратного преобразования Радона
весьма чувствительна к следующим
погрешностям реальных измерений:
Функцию p(ξ,θ) получают на дискретном массиве
точек, что затрудняет выполнение операции
дифференцирования;
Не учитываются погрешности измерений (ширина
пучка, рассеяние рентгеновского излучения,
квантовые флуктуации и пр
10.
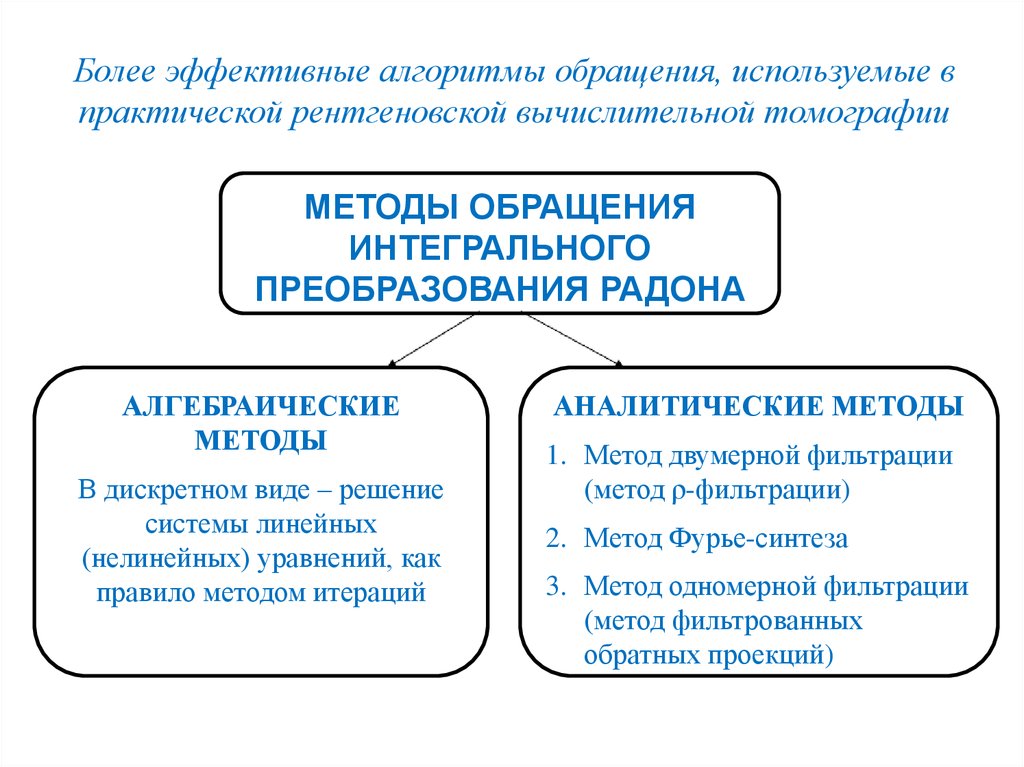
Более эффективные алгоритмы обращения, используемые впрактической рентгеновской вычислительной томографии
МЕТОДЫ ОБРАЩЕНИЯ
ИНТЕГРАЛЬНОГО
ПРЕОБРАЗОВАНИЯ РАДОНА
АЛГЕБРАИЧЕСКИЕ
МЕТОДЫ
В дискретном виде – решение
системы линейных
(нелинейных) уравнений, как
правило методом итераций
АНАЛИТИЧЕСКИЕ МЕТОДЫ
1. Метод двумерной фильтрации
(метод ρ-фильтрации)
2. Метод Фурье-синтеза
3. Метод одномерной фильтрации
(метод фильтрованных
обратных проекций)
11.
1. Метод двумерной фильтрации(метод ρ-фильтрации)
ρ-фильтрация
Состоит из двух этапов:
• Получение суммарного изображения g(x,y) с помощью операции
обратного проецирования;
• Двумерная фильтрация суммарного изображения, результатом
которой является оценка исходного изображения x, y
Операция обратного проецирования:
Для каждой проекции p(ξ,θ) находится обратная проекция b(x,y,θ):
b( x, y, ) p( x cos y sin ; ) p( , )
т.е. значение отсчета p(ξ,θ) приписываем всем точкам, лежащим
на прямой ξ=x·cosθ + y·sinθ в неподвижной системе координат.
Суммарное изображение g(x,y) получится суперпозицией всех
обратных проекций:
1
g ( x, y )
2
2
b ( x , y , ) d
0
12. Обратное проецирование
ρ-фильтрацияОбратное проецирование
Операция обратного проецирования позволяет получить
первое приближение к искомому решению g(x,y) , которое
может быть удовлетворительным для простых изображений и
сопоставимо по качеству с изображением, получаемым с
помощью традиционной нелинейной томографии.
Суммарное изображение g(x,y) связано с искомой
функцией µ(x,y) уравнением свёртки:
13. Обратное проецирование
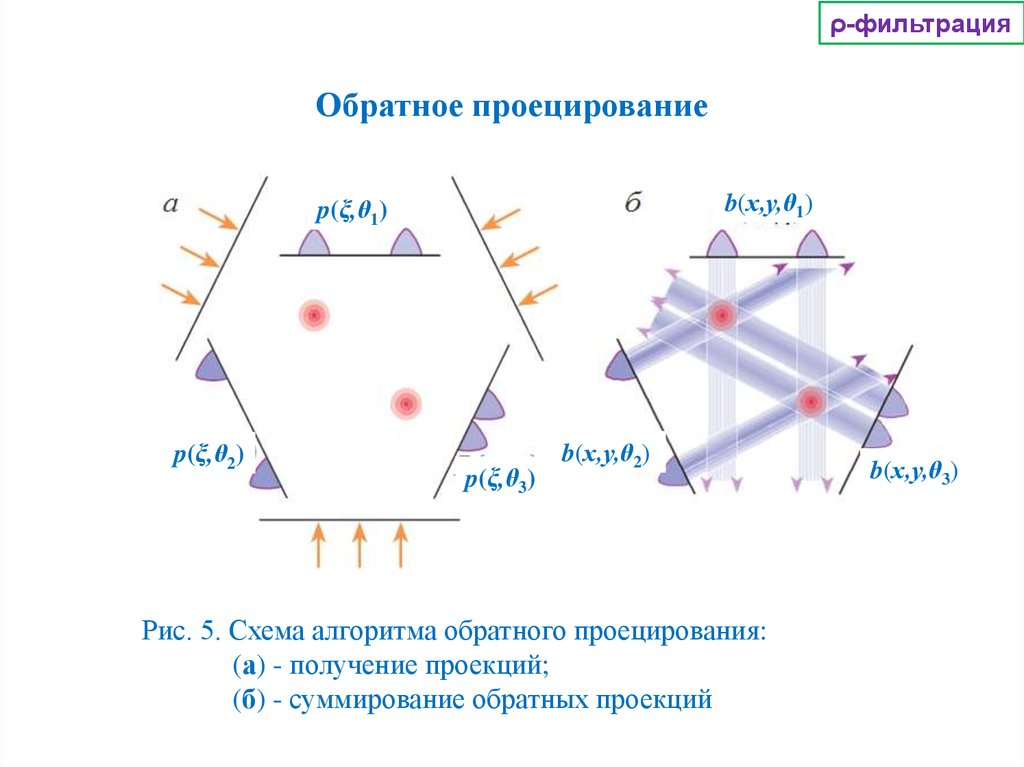
ρ-фильтрацияОбратное проецирование
b(x,y,θ1)
p(ξ,θ1)
p(ξ,θ2)
p(ξ,θ3)
b(x,y,θ2)
Рис. 5. Схема алгоритма обратного проецирования:
(а) - получение проекций;
(б) - суммирование обратных проекций
b(x,y,θ3)
14.
ρ-фильтрацияОбратное проецирование
g ( x, y )
1
( x, y )
2
3
( x, y )
4
Суммарное изображение g(x,y) связано с искомой
функцией µ(x,y) уравнением свёртки:
g ( x, y ) ( x, y ) FR
15. Двумерная фильтрация суммарного изображения
ρ-фильтрацияДвумерная фильтрация суммарного изображения
Суммарное изображение g(x,y) связано с искомой функцией µ(x,y) уравнением
свёртки:
g ( x, y) ( x, y) h2 ( x, y)
Можно показать, что ядро двумерной свёртки h2(x,y) имеет вид:
h2 ( x, y )
(1.21)
1
x2 y 2
Следовательно нужна дополнительная операция фильтрации, т.е. решение
свёртки (1.21) с известным ядром h2(x,y). Для этого необходимо перейти в
Фурье пространство и воспользоваться теоремой о двумерной свёртке:
F2{g ( x, y)} 2 F2{ ( x, y)}* F2{h2 ( x, y)}
где F2{…}-двумерное преобразование Фурье
Тогда двумерный Фурье-образ искомой функции µ(x,y) будет равен:
F2 {g ( x, y )}
F2 { ( x, y )}
2 F2 {h2 ( x, y )}
А оценка исходного изображения
1 1 F2 {g ( x, y)}
~( x, y)
F2
2
F
{
h
(
x
,
y
)}
2 2
где F2-1{…}- обратное двумерное преобразование Фурье
(1.23)
16. Двумерная фильтрация суммарного изображения
ρ-фильтрацияВместо истинного значения µ(x,y) используется оценка истинного распределения по
следующим причинам:
При измерениях проекции p(ξ,θ) определяются с некоторой ошибкой. Поэтому
проецирующая функция δ(ξ) в (1.7) строго говоря, должна быть заменена более
протяженной и физически более адекватной чётной функцией, пространственный спад которой достаточно быстро убывает. Следовательно, суммарное
изображение g(x,y) и восстановленное по (1.23) изображение будут получены с
некоторой ошибкой.
Если Фурье-образ ядра h2(x,y) будет иметь близкие к 0 значения (x,y → ∞), то
полученная оценка может сколь угодно сильно отличаться от истинного
изображения µ(x,y), что является отражением общей некорректности задачи
решения интегральных уравнений первого рода, к которым относится свёртка.
При реальных вычислениях вводят аподизирующую функцию (функцию
окна) A2(u,v) в Фурье-пространстве (u, v- декартовы координаты в фурьепространстве). Эта функция учитывает априорную информацию и регулирует
некорректную задачу решения свёртки.
Таким образом, регуляризованная оценка искомого изображения будет равна:
( x, y )
1 1 F2 {g ( x, y )}
F2 {
A2 (u , v)}
2
F2 {h2 ( x, y )}
17. Двумерная фильтрация суммарного изображения
ρ-фильтрацияДвумерная фильтрация суммарного изображения
Вычислим фурье-образ ядра Н2(u,v) в полярной системе координат.
Ядро свёртки h2(x,y) в полярной системе координат зависит только от
модуля радиус-вектора r:
h2 ( x, y )
1
1
h2 (r )
r
x2 y2
Можно показать, что фурье-образ ядра свёртки Н2(u,v) в полярной
системе координат также зависит только от модуля радиус-вектора ρ:
H 2 ( , ) F2 h2 r
1
1
H 2 ( )
u 2 v2
Поскольку Н2(ρ) зависит только от радиуса ρ, аподизирующую функцию
также выбирают зависисящей только от радиуса ρ:
A2 (u, v) A2 ( , ) A2 ( )
В качестве аподизирующей функции («окна») часто используют:
функцию в виде прямоугольного импульса, ограниченного
по полосе частот;
косинусную функцию;
синусную функцию;
обобщённую функцию Хемминга.
18.
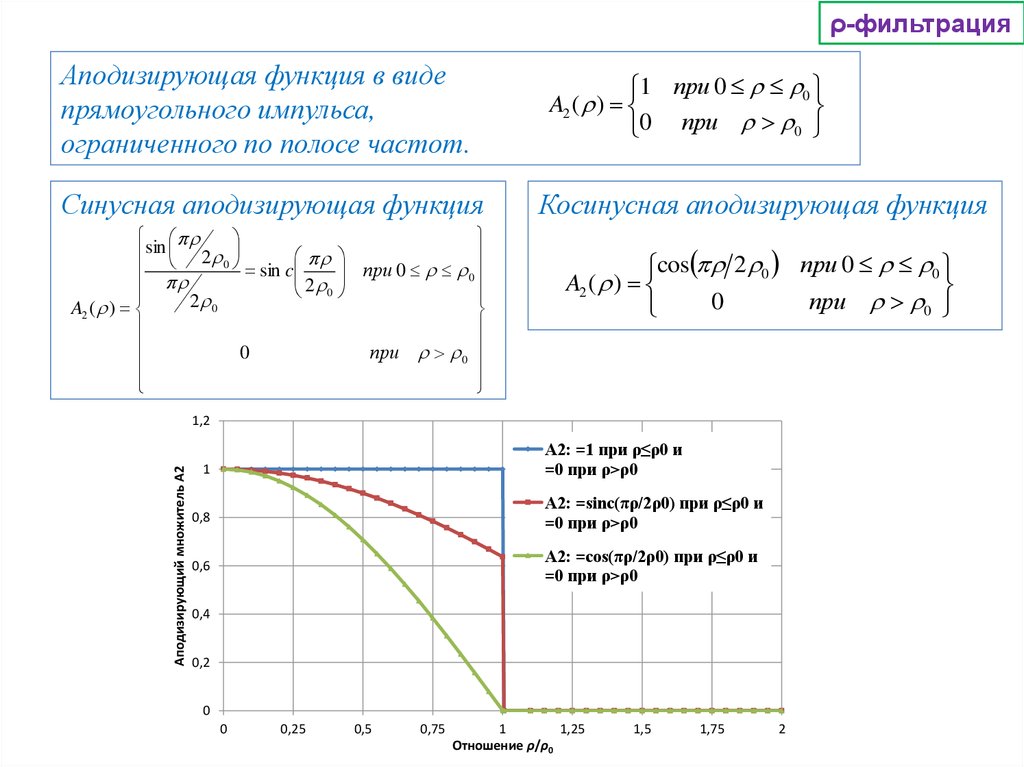
ρ-фильтрацияАподизирующая функция в виде
прямоугольного импульса,
ограниченного по полосе частот.
Синусная аподизирующая функция
sin
2 0
при 0 0
sin c
2 0
2
0
A2 ( )
0
при 0
1 при 0 0
A2 ( )
0
при
0
Косинусная аподизирующая функция
cos 2 0 при 0 0
A2 ( )
0
при
0
Аподизирующий множитель А2
1,2
А2: =1 при ρ≤ρ0 и
=0 при ρ>ρ0
1
0,8
А2: =sinc(πρ/2ρ0) при ρ≤ρ0 и
=0 при ρ>ρ0
0,6
А2: =cos(πρ/2ρ0) при ρ≤ρ0 и
=0 при ρ>ρ0
0,4
0,2
0
0
0,25
0,5
0,75
1
1,25
Отношение ρ/ρ0
1,5
1,75
2
19.
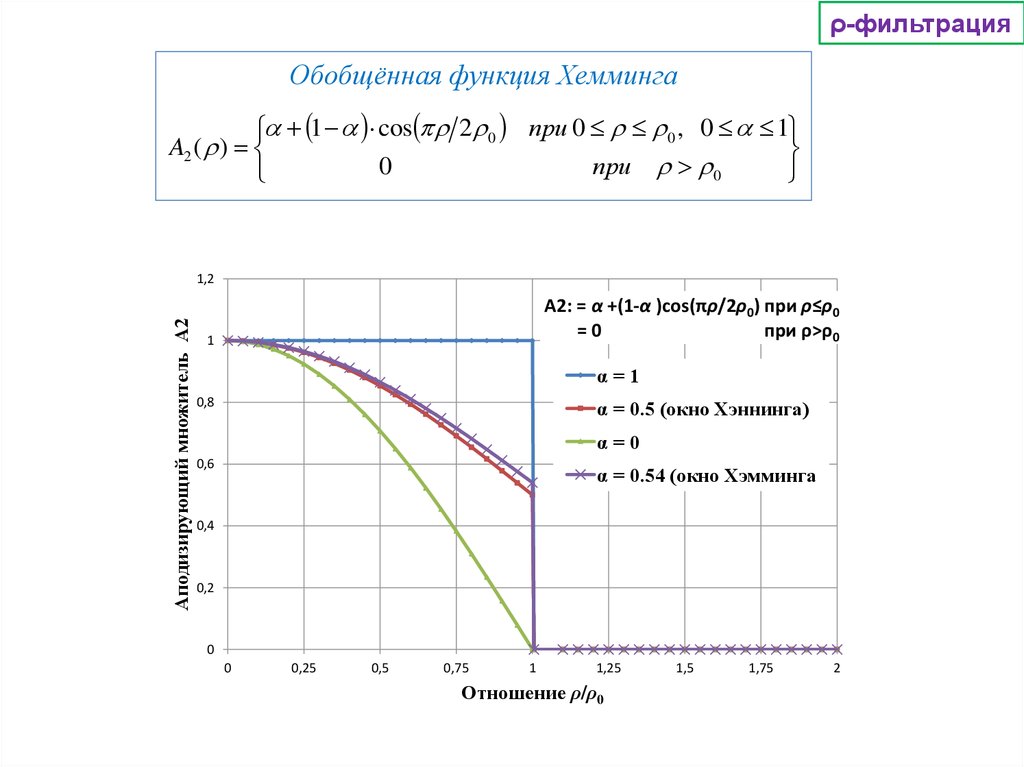
ρ-фильтрацияОбобщённая функция Хемминга
1 cos 2 0 при 0 0 , 0 1
A2 ( )
0
при
0
Аподизирующий множитель А2
1,2
А2: = α +(1-α )cos(πρ/2ρ0) при ρ≤ρ0
=0
при ρ>ρ0
1
α=1
0,8
α = 0.5 (окно Хэннинга)
α=0
0,6
α = 0.54 (окно Хэмминга
0,4
0,2
0
0
0,25
0,5
0,75
1
1,25
Отношение ρ/ρ0
1,5
1,75
2
20. 2. Метод Фурье-синтеза
Фурье-синтез2. Метод Фурье-синтеза
Данный метод обращения преобразования Радона основан на так называемой
теореме о центральном сечении, устанавливающей связь между одномерным
фурье-образом проекции p(ξ,θ) по переменной ξ и двумерным фурье-образом
искомого распределения µ(x,y).
Одномерный фурье-образ проекции p(ξ,θ) по переменной ξ в полярной системе
координат (r,φ) равен :
2
Р ( , ) F1{ p( , )}
1
2
i r cos( )
(
r
,
)
e
rdrd
0 0
[существует только в точках ξ = r·cos(θ - φ)]
Двумерный фурье-образ искомого распределения µ(x,y) в полярной системе
координат (ρ,ψ) равен :
2
1
F2 { ( x, y)} M (u, v) M ( , )
(r , )e ir cos( ) rdrd
2 0 0
Очевидно, если заменить χ на ρ, а θ на ψ, то получим соотношение:
1
M ( , )
Р ( , )
2
т.е. одномерный фурье-образ проекции p(ξ,θ) , полученной при уголе θ, является
сечением (фрагментом) двумерного фурье-образа искомого распределения µ(x,y)
по линии, проходящей через начало координат (центральное сечение) и
повернутой на угол θ.
21.
Фурье-синтезТаким образом, из одномерных фурье-образов
проекций Р(ρ, ψ) можно набрать
(синтезировать) двумерный фурье-образ
искомого изображения М(ρ, ψ), которое затем
можно восстановить с помощью двумерного
обратного преобразования Фурье.
1
( x, y)
F2- 1 Р ( , )
2
Отсчёты фурье-образа M(ρ,ψ) искомой функции
µ(x,y) находятся на полярной сетке, а обратное
преобразование Фурье необходимо выполнять на
декартовой сетке. Поэтому декартовы отсчёты
M(u,v) находят путем интерполяции полярных
отсчётов с использованием, как правило, линейной
интерполяции по ближайшим четырем отсчётам:
MД
М П1 M П 2
d
d
1 2
1 1
d
1 d2
M П3 M П4
d3 d4
1 1
d3 d4
Мд — декартов отсчёт;
Мп1 - Мп4 — полярные отсчеты;
d1 - d4 — расстояния от декартова отсчёта до
соответствующих полярных отсчётов.
22.
Фурье-синтезТаким образом, метод фурье-синтеза включает в себя
следующую последовательность действий:
Одномерное быстрое преобразование Фурье
Интерполяция данных в Фурье-пространстве
Обратное двумерное быстрое преобразование Фурье
(БПФ)1
ИНТЕРПОЛЯЦИЯ
(ОБПФ)2
Центральное сечение
двумерного
преобразования Фурье
Алгоритм реконструкции, основанный на двумерном преобразовании
Фурье, относится к наиболее быстрвм алгоритмам и позволяет начинать
обработку экспериментальных данных в процессе измерений.
23. 3. Метод одномерной фильтрации (метод фильтрованных обратных проекций)
Метод ФОП3. Метод одномерной фильтрации
(метод фильтрованных обратных проекций)
Последовательность действий в данном методе:
Одномерная фильтрация каждой проекции;
Операция обратного проецирования, результатом которой
является оценка искомого изображения.
Выражение для отфильтрованной обратной проекции
имеет вид:
f ( , ) p( 0 , )h1 ( 0 )d 0
[oдномерная функция ядра свертки h1(ξ)
пока неизвестна и подлежит определению]
На втором этапе необходимо произвести операцию обратного
проецирования, т.е. найти обратную проекцию b(x,y,θ):
b( x, y, ) f ( x cos y sin ; )
24.
Метод ФОПи получить суммарное изображение , которое и должно
быть оценкой искомого распределения µ(x,y):
1
( x, y )
2
2
1
b
(
x
,
y
,
)
d
0
2
2
f ( x cos y sin ; )d
0
Можно показать, что функция ядра свертки в Фурьепространстве Н1(χ) имеет вид:
H1 ( )
1
2 2
Тогда функция ядра свертки h1(ξ) в интегральном
представлении имеет вид:
1
h1 ( )
4
e i d
Поскольку при χ → ∞ значение функции ядра свертки
h1(ξ) → ∞, то необходимо (как в методе ρ-фильтрации)
ввести аподизирующую функцию А1(χ):
1
h1 ( )
4
ei A1 ( )d
25.
Метод ФОПВ качестве аподизирующих функций используют те же функции, что и в
методе ρ-фильтрации. Рассмотрим, например, аподизирующую функцию
в виде прямоугольного импульса, ограниченного по полосе частот :
1 при 0 0
A1 ( )
0
при
0
Тогда функция ядра свертки h1(ξ) будет иметь следующий вид:
02
h1 ( )
2
1
2 0
sinc( 0 ) 2 sinc ( 2 )
В реальных измерениях проекции p(ξ,θ) получают в виде набора
дискретных значений p(ξn,θ) = p(n·Δξ,θ), n = 0; ±1; ±2; …., поэтому
необходимо вычислить значения функции ядра в точках измерений
h1((ξn) = h1(n·Δξ).
26.
Метод ФОПСогласно теореме Котельникова, если непрерывная функция f(x) имеет
фурье-образ, отличный от нуля только на интервале [-χ0, +χ0], то она может
быть представлена своим дискретным отсчётом в виде ряда:
f ( x)
n
n
n
f
0
n
sinc 0 x
0
Т.к. используемая аподизирующая функция зануляет фурье-образ Н1(χ)
ядра h1(ξ) вне интервала [-χ0, +χ0], то для предотвращения потери
информации мы должны снимать отсчёты с дискретностью Δξ ≤ π / χ0 .
Следовательно, дискретные значения функции ядра свертки
h1(n·Δξ) будут равны:
02
1
n
h1 (n )
sinc 0 n sinc 2 0
2
2
2
27.
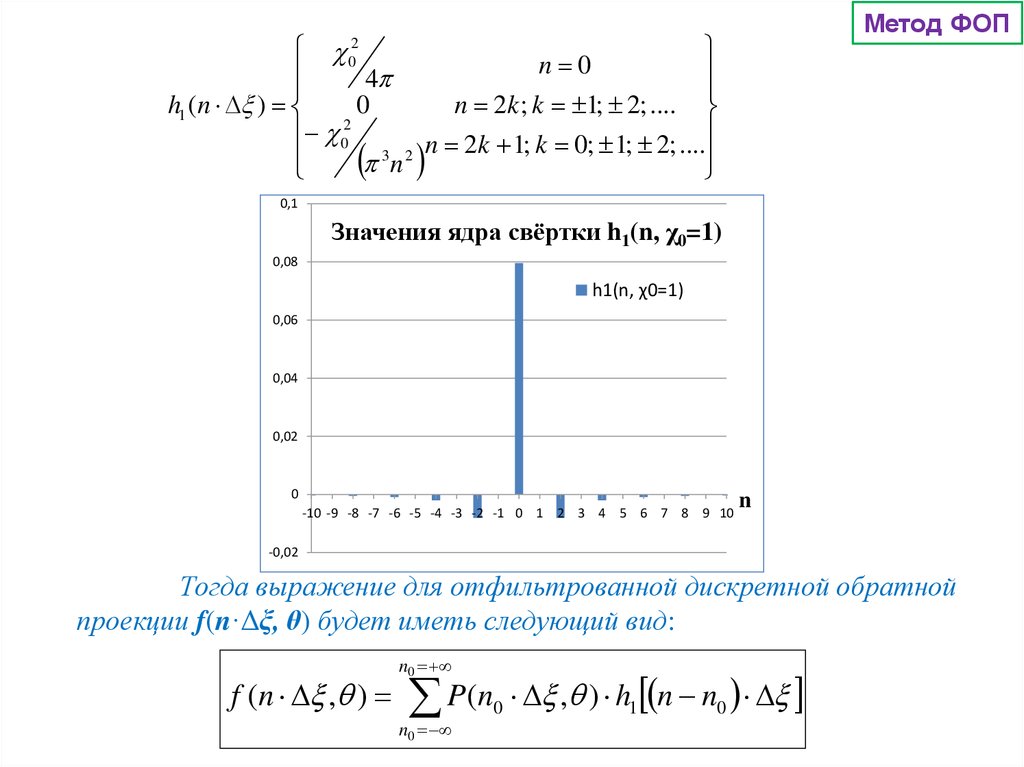
Метод ФОПn
0
4
h1 (n )
0
n 2k ; k 1; 2; ....
2
0
3 2 n 2k 1; k 0; 1; 2; ....
n
2
0
0,1
Значения ядра свёртки h1(n, χ0=1)
0,08
h1(n, χ0=1)
0,06
0,04
0,02
0
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
n
-0,02
Тогда выражение для отфильтрованной дискретной обратной
проекции f(n·Δξ, θ) будет иметь следующий вид:
f (n , )
n0
P(n
n0
0
, ) h1 n n0
28.
Метод ФОПСвязь между числом радиальных Nξ и угловых Nθ отсчётов.
Пусть Н – диаметр объекта исследования.
Число отсчётов в проекции Nξ равно:
N
H
H
2 0 H
0
Чтобы изображение имело одинаковое по всем направлениям разрешение,
наивысшие пространственные частоты должны иметь одинаковый шаг
дискретизации в радиальном и азимутальном направлениях в окрестности
ρ0 в Фурье-пространстве.
Число угловых отсчётов Nθ выбирается таким образом, чтобы оно было
равно числу проекций в области углов 0 ≤ θ ≤ 180º.
Шаг в радиальном направлении θ равен
2 0 2 0
ΔΘ
ρ Шаг в азимутальном направлении ρ равен
ρ
N
Н
0
Приравняв интервалы между отсчётами в Фурье-пространстве в радиальном
2 0
и азимутальном
направлении при ρ = ρ0, получим:
N
N
29.
0N
2 0
N
тогда:
N
2
Метод ФОП
N
При равномерной выборке данных изображения угол проекции,
выраженный в радианах, изменяется с шагом:
2
2
2
N N
N H
H
2
При числе отсчётов в проекции Nξ = 253 ÷ 1024
интервал дискретизации по углу ΔΘ = 2/Nξ = 0,45º ÷ 0,11º,
а общее число отсчётов будет равно: Nξ×NΘ = (1 ÷ 16)·105.
Пример:
при Н = 420 мм и ширине щели коллиматора ω = 3мм (ω = 1/ρ0) получим:
Nξ ≥ 2 ρ0Н = 2·0,33·420 = 277;
Δξ = ω/2 = 3/2 = 1,5 [мм]
NΘ = (π/2)·Nξ = 1.57·277 = 435
ΔΘ = π/NΘ = 3.14/435 = 0.072 [рад] = 0,41º
Nξ×NΘ = 277·435 = 1,2·105.
Эти данные примерно соответствуют параметрам серийных томографов.
30.
КОНЕЦ 1-ОЙ ЧАСТИСПАСИБО ЗА ВНИМАНИЕ
30

























 Медицина
Медицина Физика
Физика








