Способы математического описания САУ. Основы автоматизации технологических процессов нефтегазового производства. Лекция 2

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет
императрицы Екатерины II
Основы автоматизации
технологических процессов
нефтегазового производства
Лекция 2
НИКИТИНА Л.Н., к.т.н., доцент кафедры АТПП
г. Санкт-Петербург
2024
1|29

2. Способы математического описания САУ

Дифференциальные уравнения
Передаточные функции
Временные характеристики
Частотные характеристики
2|29

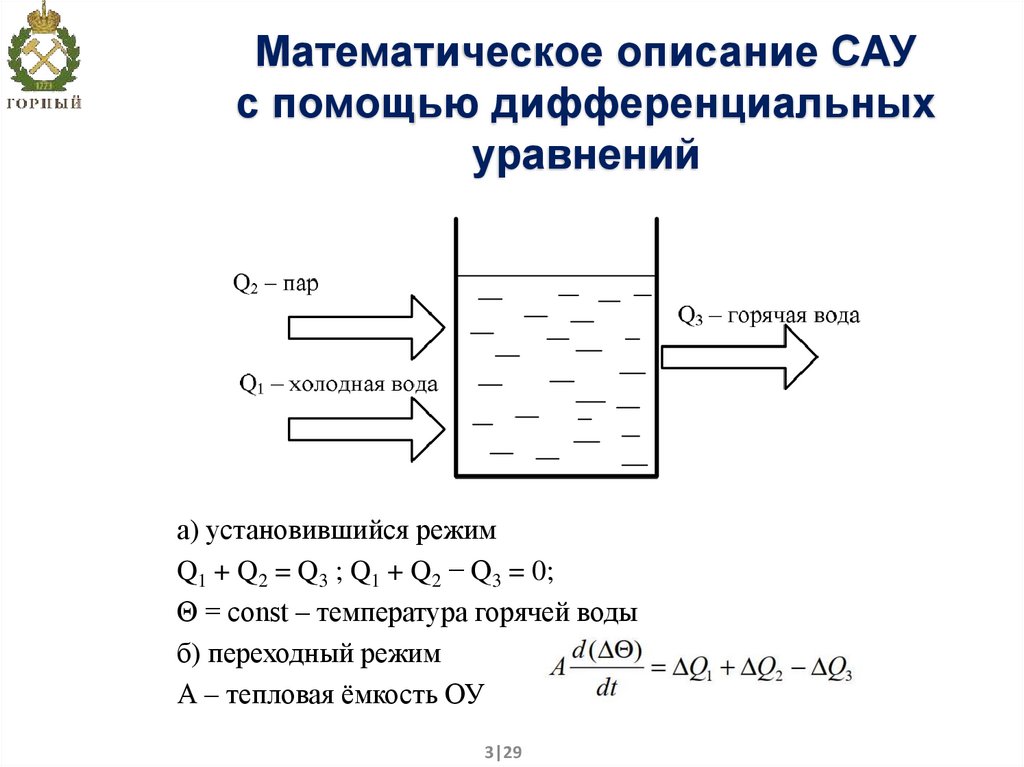
3. Математическое описание САУ с помощью дифференциальных уравнений

а) установившийся режим
Q1 + Q2 = Q3 ; Q1 + Q2 − Q3 = 0;
Θ = const – температура горячей воды
б) переходный режим
А – тепловая ёмкость ОУ
3|29

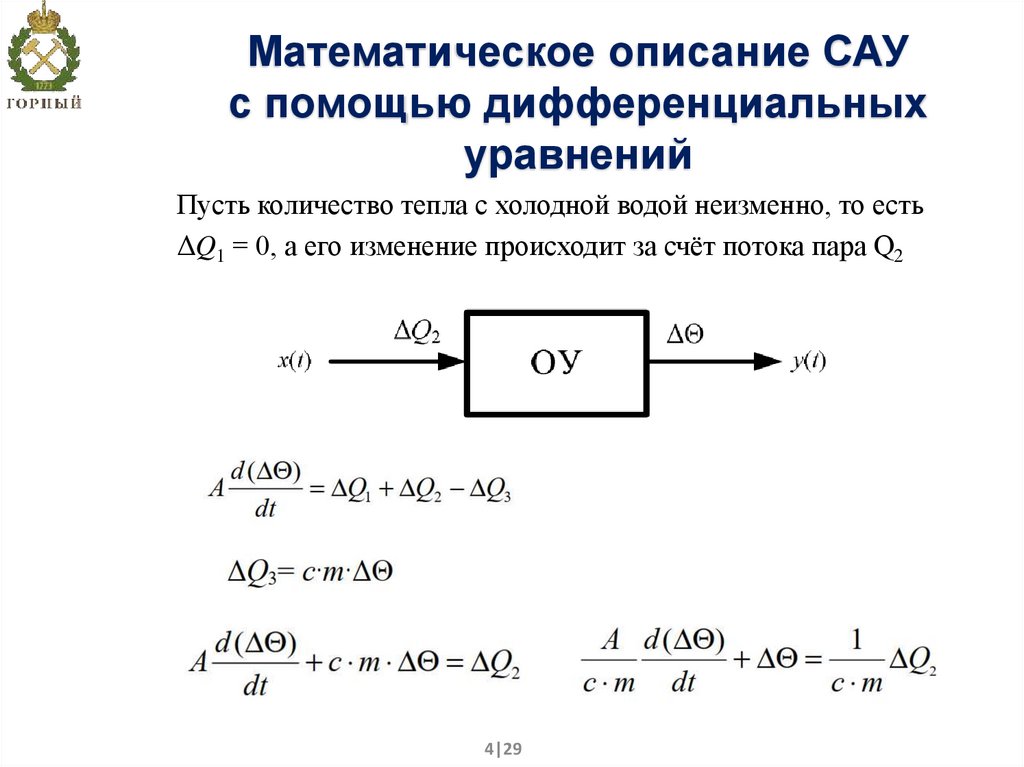
4. Математическое описание САУ с помощью дифференциальных уравнений

Пусть количество тепла с холодной водой неизменно, то есть
ΔQ1 = 0, а его изменение происходит за счёт потока пара Q2
4|29

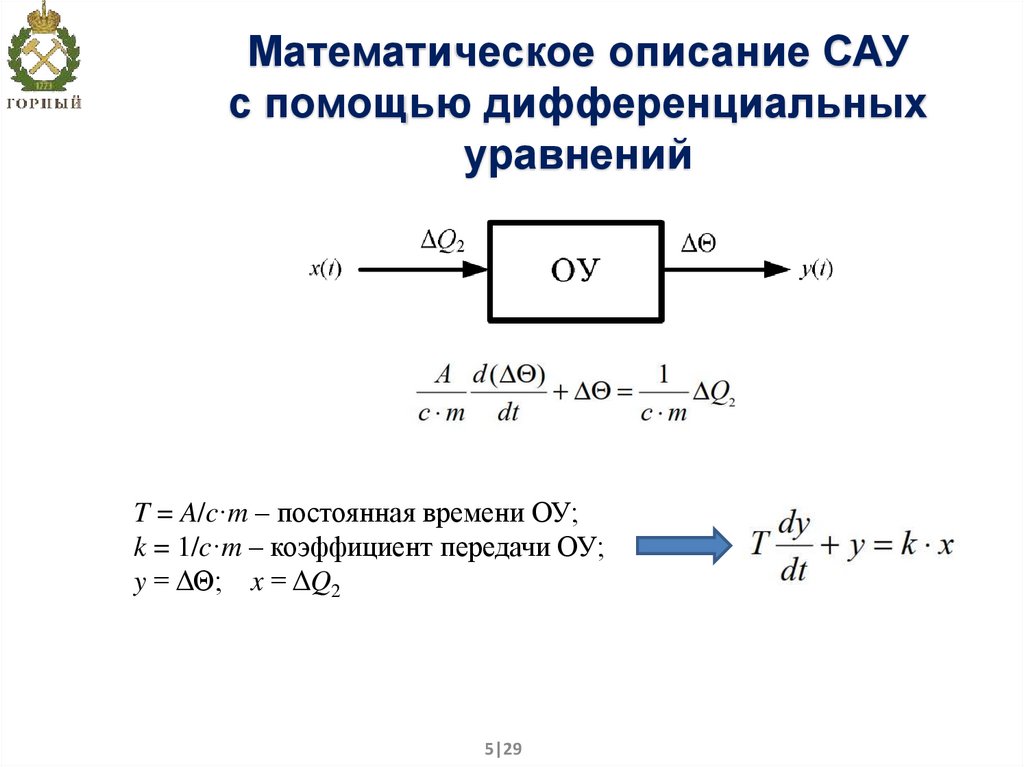
5. Математическое описание САУ с помощью дифференциальных уравнений

T = A/c·m – постоянная времени ОУ;
k = 1/c·m – коэффициент передачи ОУ;
y = ΔΘ; x = ΔQ2
5|29

6. Математическое описание САУ с помощью дифференциальных уравнений

Коэффициенты a0 , a1 , , an , b0 , , bm
называются параметрами. Иногда параметры изменяются во
времени, тогда элемент называют нестационарным или с
переменными параметрами.
Характеристическое уравнение – алгебраическое уравнение, степень
и коэффициенты которого совпадают с порядком и коэффициентами
левой части линейного дифференциального уравнения
.
6|29

7. Математическое описание САУ с помощью передаточных функций

Наиболее распространенным методом описания и анализа АСУ является
операционный метод (метод операционного исчисления), в основе
которого лежит прямое интегральное преобразование Лапласа для
непрерывных функций
Это преобразование устанавливает соответствие между функцией
действительной переменной t и функцией комплексной переменной р
= + j . Функцию , входящую в интеграл Лапласа, называют
оригиналом, а результат интегрирования –изображением функции по
Лапласу
Обратное преобразование Лапласа
7|29

8. Математическое описание САУ с помощью передаточных функций

Свойства преобразования Лапласа:
1)
2)
3)
4)
8|29

9. Математическое описание САУ с помощью передаточных функций

При нулевых начальных условиях (t = 0) выходная
величина x(0) и все её производные x'(0) … xn-1(0) = 0.
Тогда
9|29

10. Математическое описание САУ с помощью передаточных функций

K ( p) bm p m bm 1 p m 1 ... b0 y ( p)
W ( p)
n
n 1
D( p) an p an 1 p ... a0 x( p)
Передаточная функция отношение изображения выходного сигнала к
изображению входного сигнала при нулевых
начальных условиях.
10|29

11. Математическое описание САУ с помощью передаточных функций

Собственный оператор Входной оператор -
D( p ) an p n an 1 p n 1 ... a0
K ( p ) bm p m bm 1 p m 1 ... b0
Значение переменной р, при которой передаточная функция
обращается в бесконечность, называется полюсом передаточной
функции. Полюсами являются корни собственного оператора.
Значение переменной р, при которой передаточная функция
обращается в ноль, называется нулем передаточной функции.
Нулями являются корни входного оператора.
.
11|29

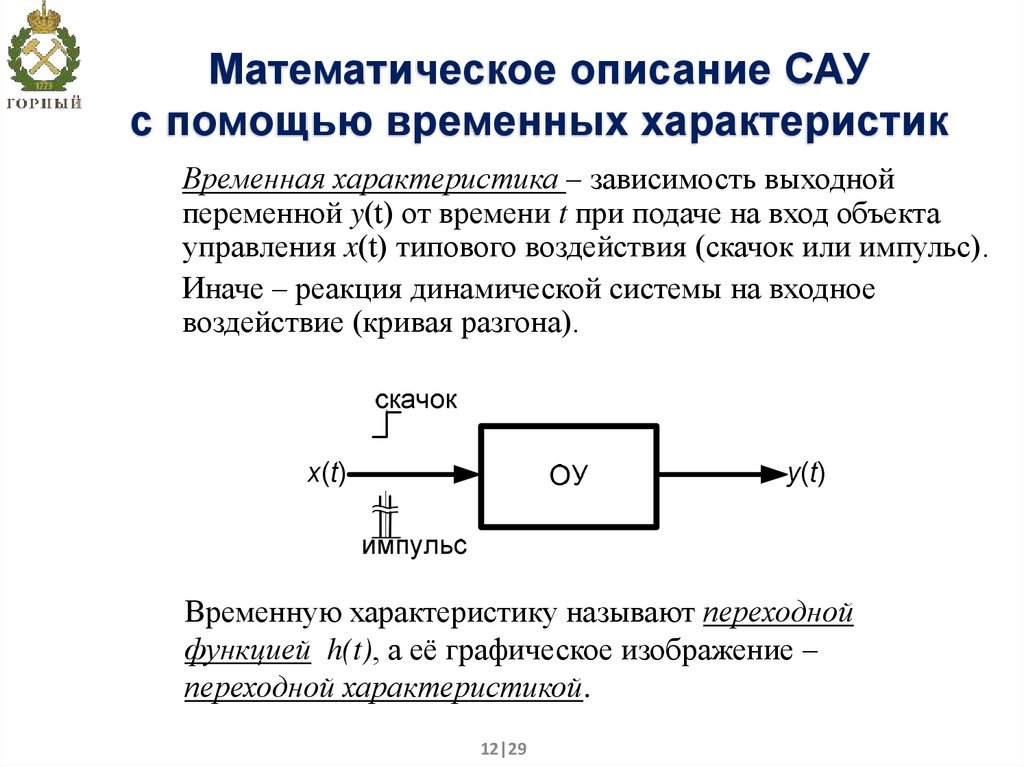
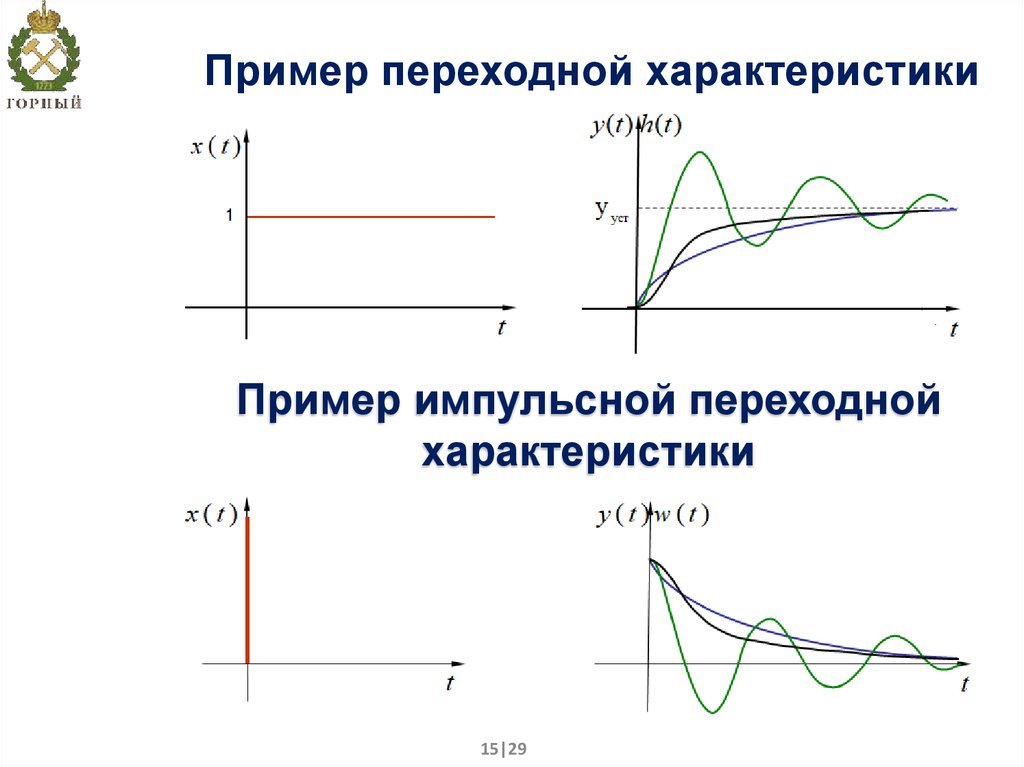
12. Математическое описание САУ с помощью временных характеристик

Временная характеристика – зависимость выходной
переменной y(t) от времени t при подаче на вход объекта
управления x(t) типового воздействия (скачок или импульс).
Иначе – реакция динамической системы на входное
воздействие (кривая разгона).
Временную характеристику называют переходной
функцией h(t), а её графическое изображение –
переходной характеристикой.
12|29

13. Математическое описание САУ с помощью временных характеристик

Скачок – единичное ступенчатое входное воздействие
x(t), которое часто возникает в системе при её
включении (отключении) и/или резком изменении
заданного режима.
13|29

14. Математическое описание САУ с помощью временных характеристик

Импульс – мгновенное (кратковременное) изменение входного
воздействия x(t). Используется для имитации возмущающего
воздействия на систему. Для его описания используют δ-функции.
Под дельта функцией понимается импульс бесконечно малой
продолжительности и бесконечно большой амплитуды с
площадью равной 1.
Импульсная переходная функция (t) равна производной от
переходной функции h(t)
14|29

15. Пример переходной характеристики

Пример импульсной переходной
характеристики
15|29

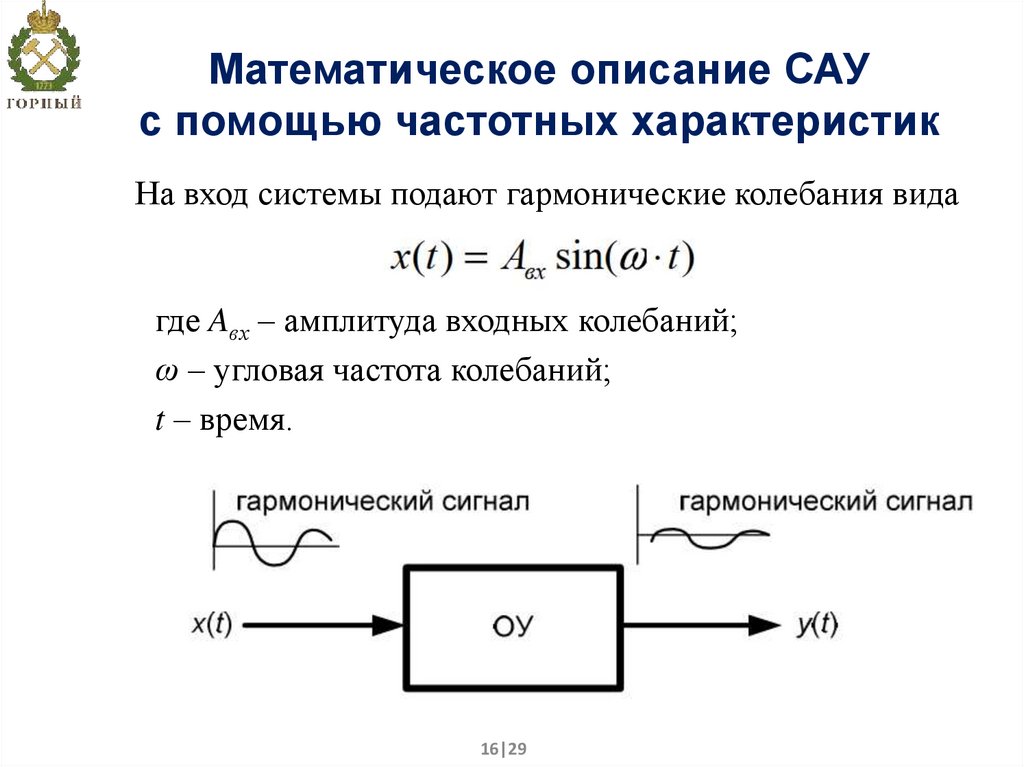
16. Математическое описание САУ с помощью частотных характеристик

На вход системы подают гармонические колебания вида
где Aвх – амплитуда входных колебаний;
ω – угловая частота колебаний;
t – время.
16|29

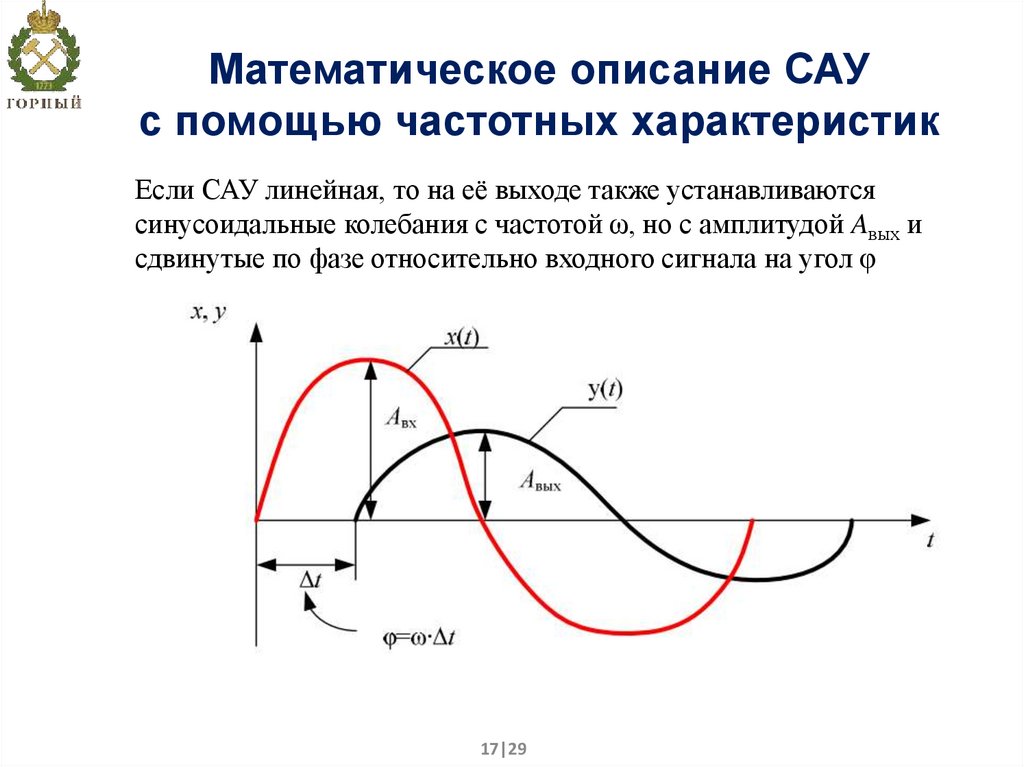
17. Математическое описание САУ с помощью частотных характеристик

Если САУ линейная, то на её выходе также устанавливаются
синусоидальные колебания с частотой ω, но с амплитудой Aвых и
сдвинутые по фазе относительно входного сигнала на угол φ
17|29

18. Математическое описание САУ с помощью частотных характеристик

Запись в комплексной форме
W ( j ) A( )e
18|29
j ( )

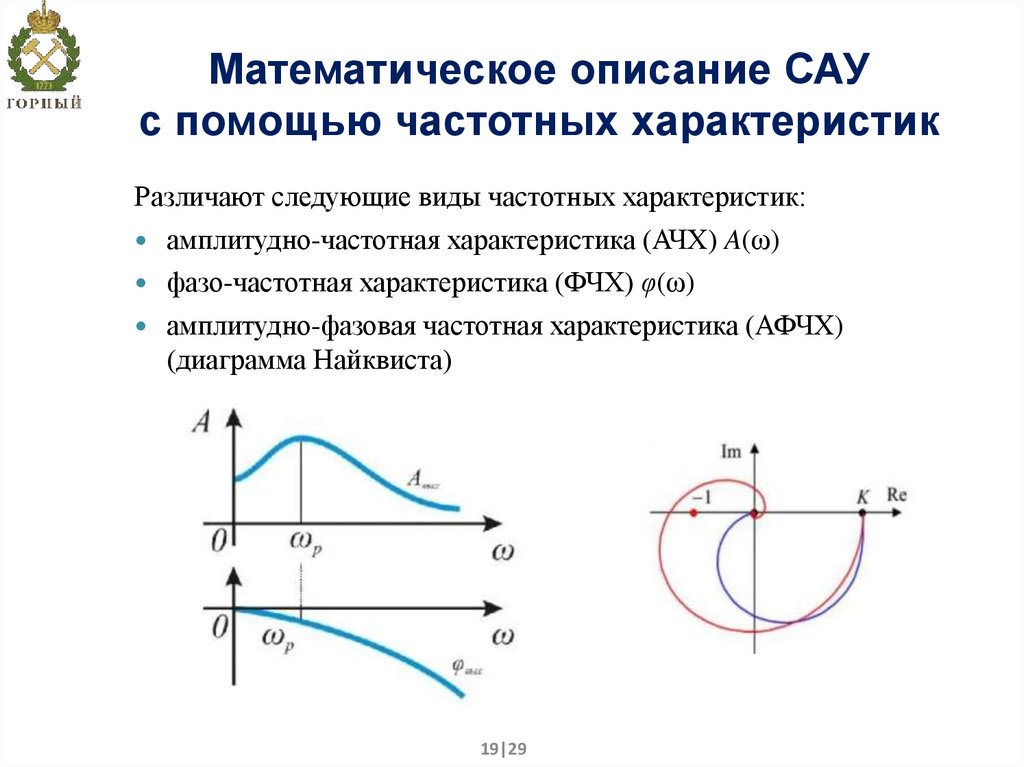
19. Математическое описание САУ с помощью частотных характеристик

Различают следующие виды частотных характеристик:
амплитудно-частотная характеристика (АЧХ) A(ω)
фазо-частотная характеристика (ФЧХ) φ(ω)
амплитудно-фазовая частотная характеристика (АФЧХ)
(диаграмма Найквиста)
19|29

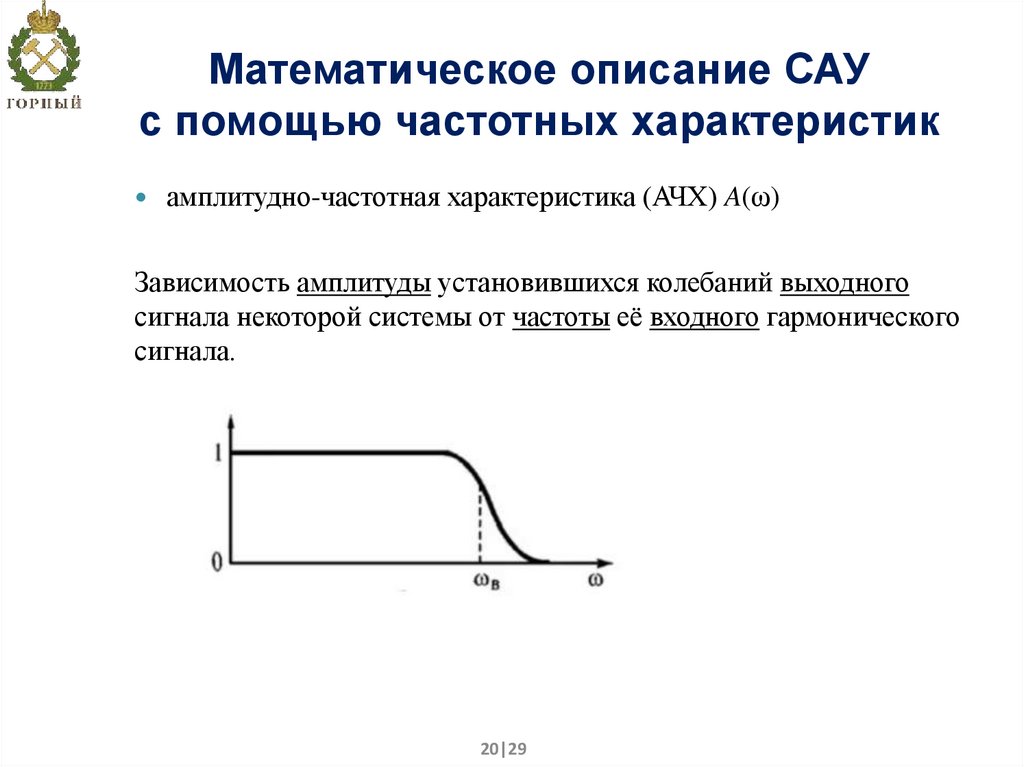
20. Математическое описание САУ с помощью частотных характеристик

амплитудно-частотная характеристика (АЧХ) A(ω)
Зависимость амплитуды установившихся колебаний выходного
сигнала некоторой системы от частоты её входного гармонического
сигнала.
20|29

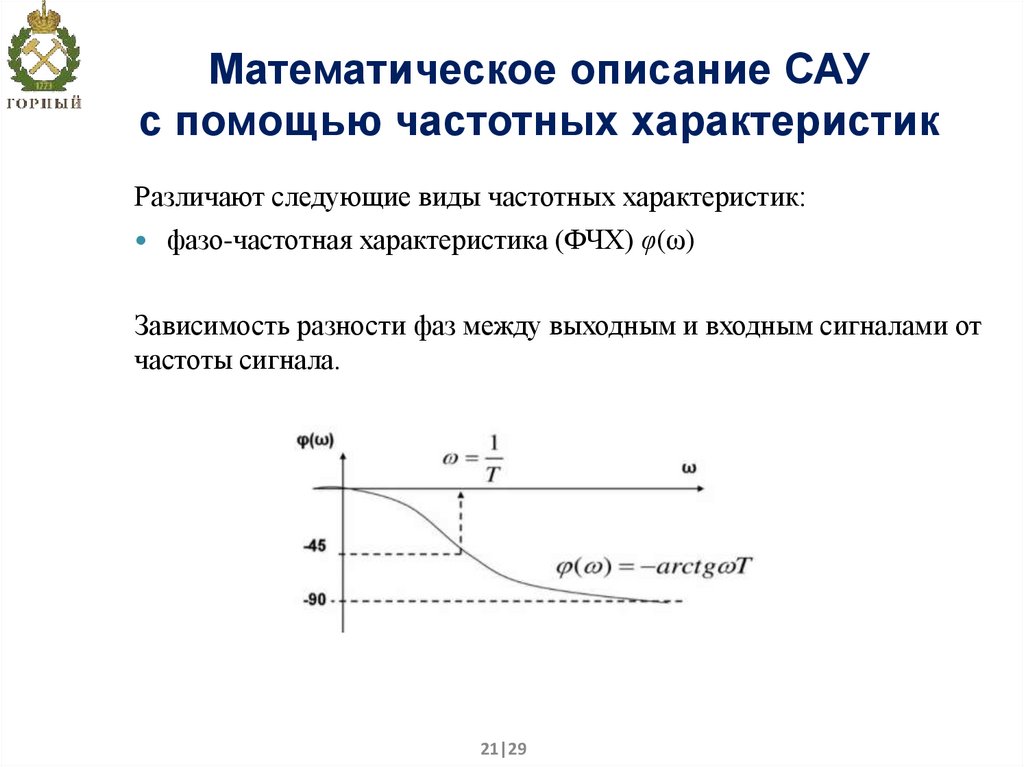
21. Математическое описание САУ с помощью частотных характеристик

Различают следующие виды частотных характеристик:
фазо-частотная характеристика (ФЧХ) φ(ω)
Зависимость разности фаз между выходным и входным сигналами от
частоты сигнала.
21|29

22. Математическое описание САУ с помощью частотных характеристик

амплитудно-фазовая частотная характеристика (АФЧХ)
Каждому фиксированному значению частоты соответствует
комплексное число
, которое на комплексной плоскости
можно изобразить вектором, имеющим длину A и угол поворота φ.
При изменении частоты от нуля до бесконечности вектор
поворачивается вокруг начала координат, при этом одновременно
изменяется длина вектора. Кривая, которую при этом опишет конец
вектора, и есть АФЧХ (годограф). Проекции вектора на
действительную и мнимую оси называют соответственно
действительной и мнимой частотными характеристиками и
обозначают P(ω) и Q(ω), что позволяет записать
22|29

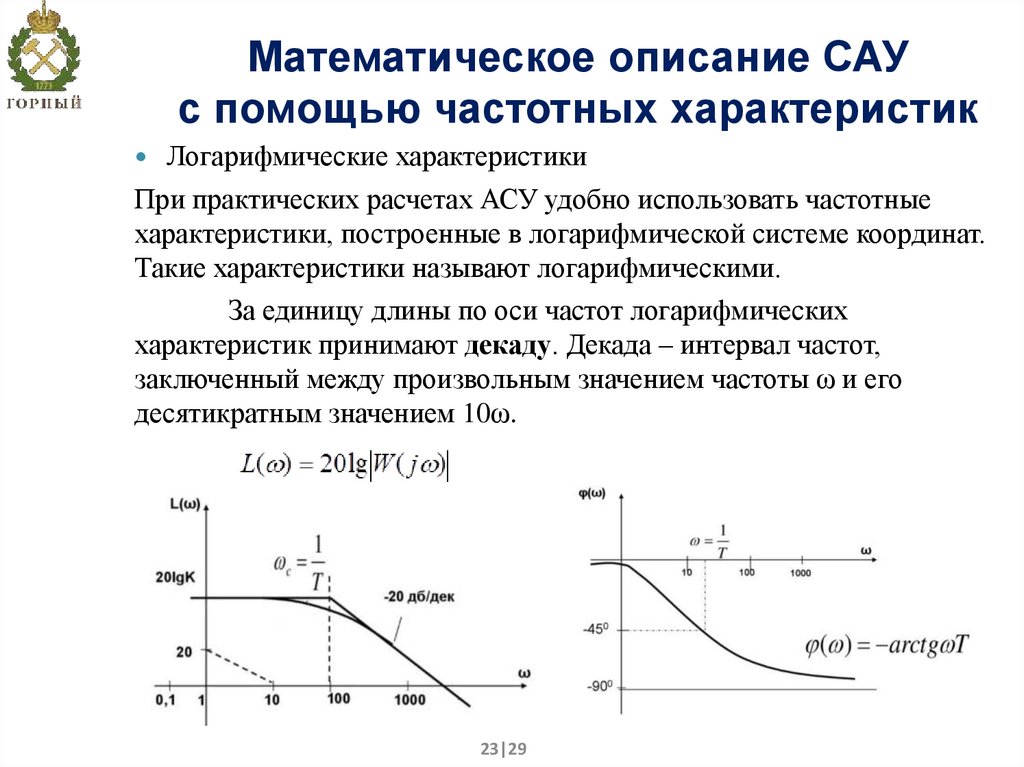
23. Математическое описание САУ с помощью частотных характеристик

Логарифмические характеристики
При практических расчетах АСУ удобно использовать частотные
характеристики, построенные в логарифмической системе координат.
Такие характеристики называют логарифмическими.
За единицу длины по оси частот логарифмических
характеристик принимают декаду. Декада – интервал частот,
заключенный между произвольным значением частоты ω и его
десятикратным значением 10ω.
23|29

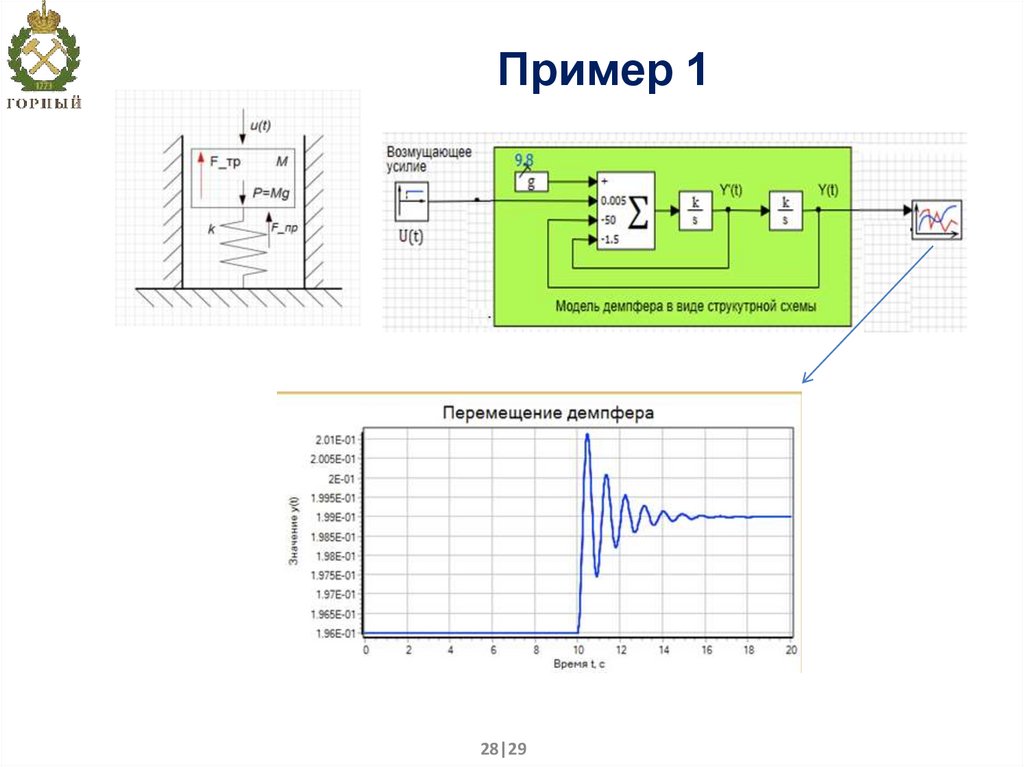
24. Пример 1

Модель механического демпфера.
Положение поршня – это функция Y(t),
сверху на него воздействует возмущающая
сила (U(t)), на стенках поршня действует
сила вязкого трения (Fтр(t)).
Согласно 2-му закону Ньютона ускорение
тела пропорционально сумме сил,
действующих на тело.
где m – масса тела; Fj - силы, воздействующие на тело (поршень
демпфера). Подставляя в уравнение все силы (сила тяжести, сила
сопротивления пружины, сила вязкого трения), имеем
Считаем, что в нулевой момент времени поршень находится в
равновесии. Тогда начальное положение поршня - y0 , скорость и
ускорение равны 0.
24|29

25. Пример 1

Для начальных условий
Данное уравнение позволяет посчитать, в каком положении будет
поршень при различных нагрузках. Это статическая характеристика:
приложили силу - получили перемещение.
Согласно теории автоматического
управления предлагается рассматривать
систему не в абсолютных значениях, а в
отклонениях от равновесного состояния.
25|29

26. Пример 1

В начальный момент система находится в состоянии равновесия, а
сумма трех сил в состоянии равновесия равна нулю, можно упростить
уравнение. В итоге получаем
Для приведения уравнения к каноническому виду, нужно все части
уравнения разделить на k, перенести в правую часть множители с
выходными значения у(t), а в левую – с входными воздействиями
u(t).
26|29

27. Пример 1

оператор дифференцирования
d
p
dt
Запись в операторной
форме
k1
W ( p) 2 2
(T2 p T1 p 1)
27|29

28. Пример 1

28|29

29. Пример 2

ОУ
X
Y
Модель гидравлической емкости.
Уровень жидкости в емкости L – это функция Y(t).
Приток жидкости (F1(t)), сток жидкости (F2(t)), коэффициент открытия
дросселя α. При α = const уровень жидкости зависит от разницы F1 – F2.
В динамическом режиме
29|29