Момент инерции. Теорема Штейнера. Кинетическая энергия вращательного движения твердого тела. (Лекция 5)

1. Лекция 5

1

2.

Контрольный вопрос
Две частицы обладают одинаковыми кинетическими
энергиями. Величины их импульсов соотносятся как:
а) p1 < p2,
б) p1 = p2,
в) p1 > p2,
г) невозможно определить.
2
p
T
2m
Масса тел неизвестна – г).
2

3.

Содержание предыдущей лекции
Механическая энергия
• Столкновение тел.
Кинематика и динамика вращательного движения
• Кинематика вращательного движения: угловая скорость и
угловое ускорение, их связь с линейной скоростью и
ускорением.
• Момент силы. Уравнение моментов.
3

4.

Содержание сегодняшней лекции
Кинематика и динамика вращательного движения
• Момент инерции. Теорема Штейнера. Кинетическая энергия
вращательного движения твердого тела.
• Основное уравнение динамики вращательного движения
твердого тела с закрепленной осью вращения.
• Момент импульса тела. Закон сохранения момента
импульса.
• Гироскопические силы. Гироскопы и их применение в
технике.
Релятивистская механика
• Принцип относительности Галилея.
4

5.

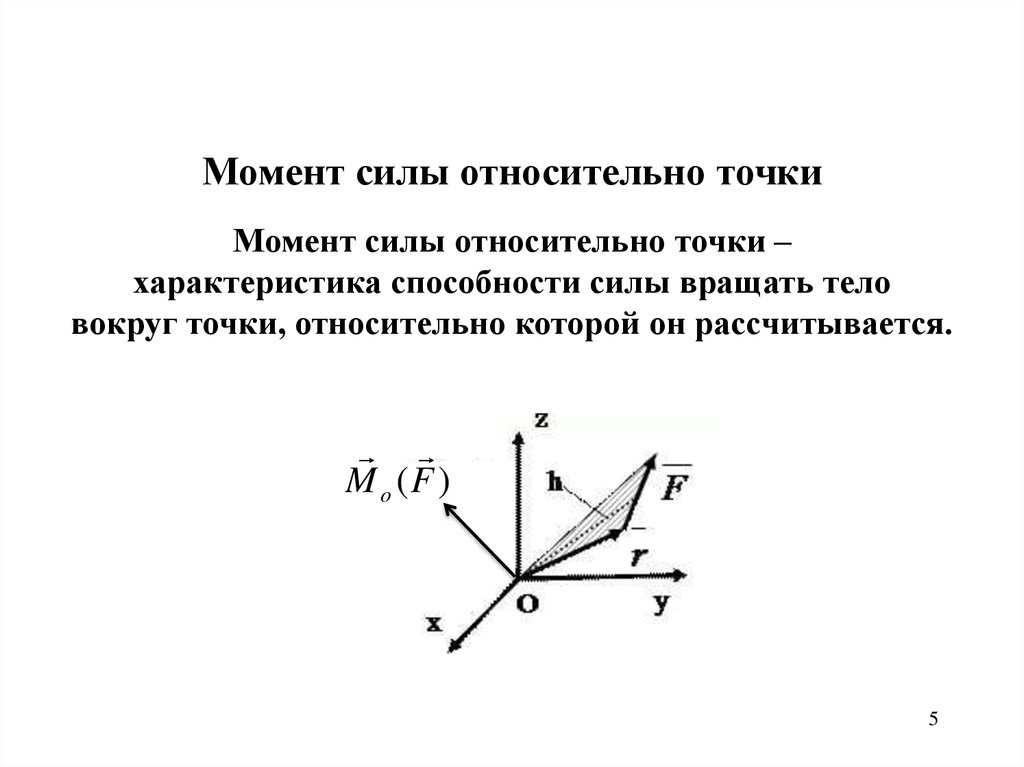
Момент силы относительно точки
Момент силы относительно точки –
характеристика способности силы вращать тело
вокруг точки, относительно которой он рассчитывается.
M o (F )
5

6.

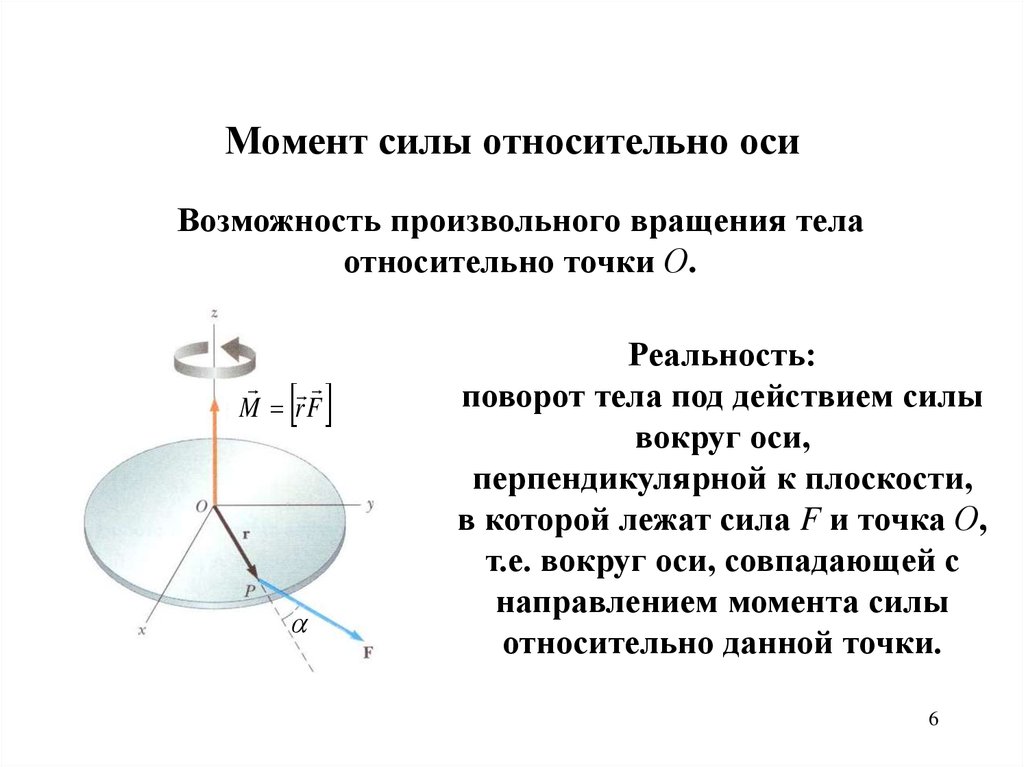
Момент силы относительно оси
Возможность произвольного вращения тела
относительно точки О.
M rF
Реальность:
поворот тела под действием силы
вокруг оси,
перпендикулярной к плоскости,
в которой лежат сила F и точка О,
т.е. вокруг оси, совпадающей с
направлением момента силы
относительно данной точки.
6

7.

Момент силы относительно оси
M
Проекция вектора
на некоторую ось,
проходящую через точку О,
относительно которой определен вектор M ,
называется моментом силы относительно этой оси:
M z r F пр z .
M z rF
пр z
M o (F )
7

8.

M rF
M o (F )
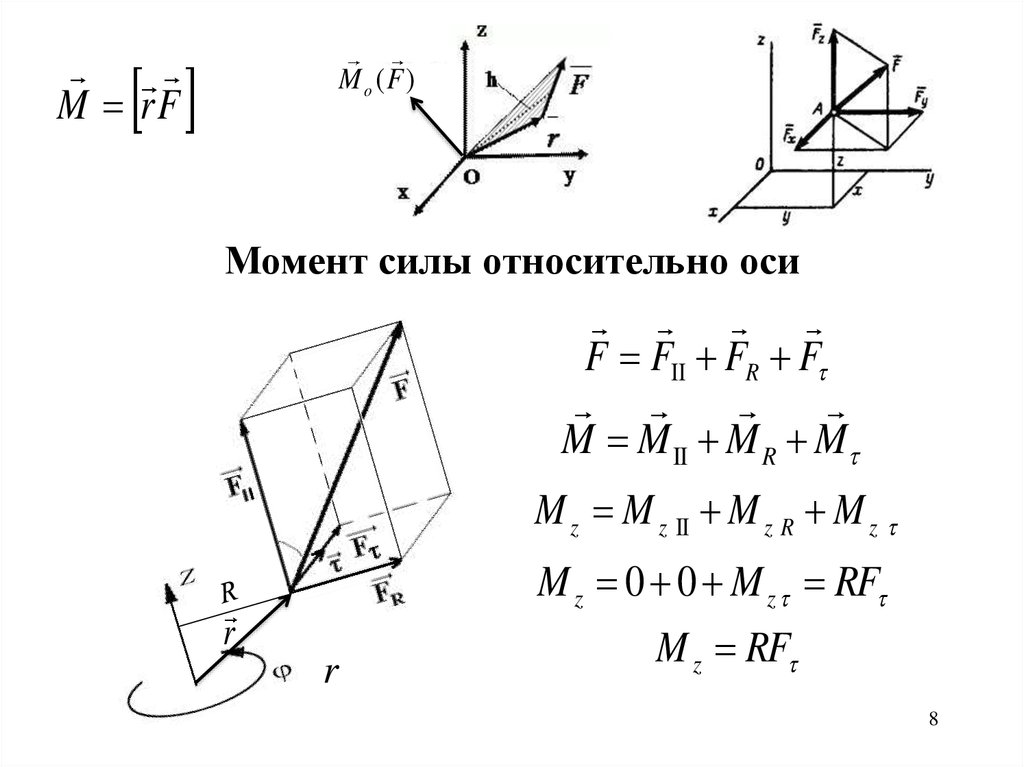
Момент силы относительно оси
F FII FR F
M M II M R M
M z M z II M z R M z
M z 0 0 M z RF
r
r
M z RF
8

9.

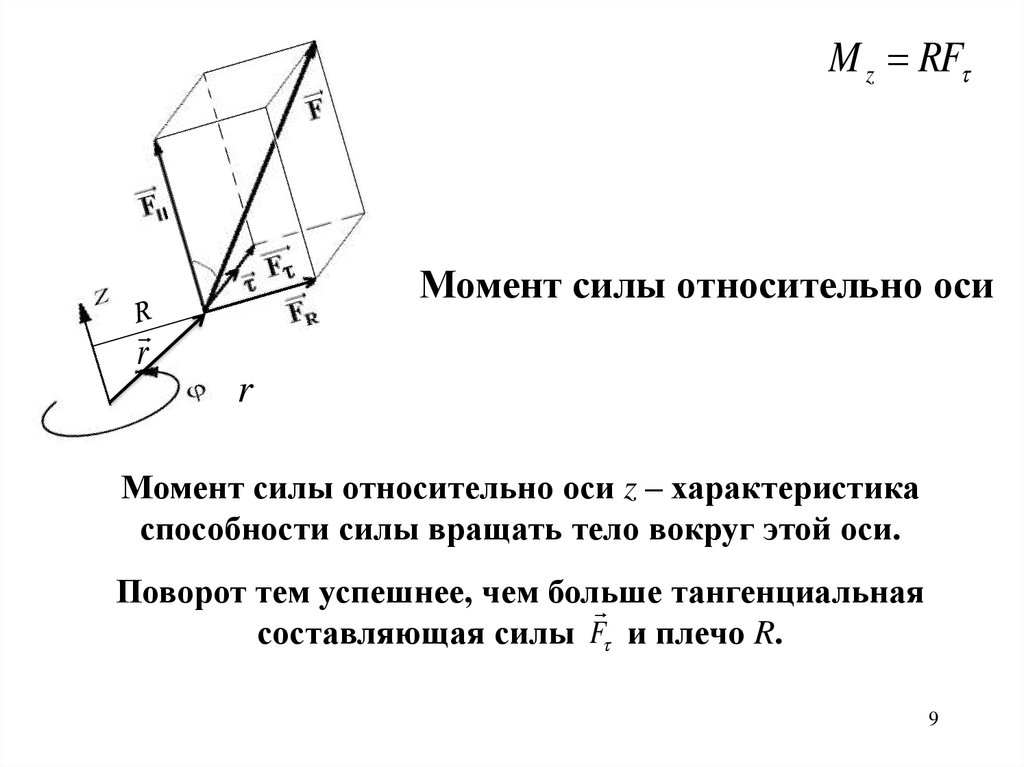
M z RF
Момент силы относительно оси
r
r
Момент силы относительно оси z – характеристика
способности силы вращать тело вокруг этой оси.
Поворот тем успешнее, чем больше
тангенциальная
составляющая силы F и плечо R.
9

10.

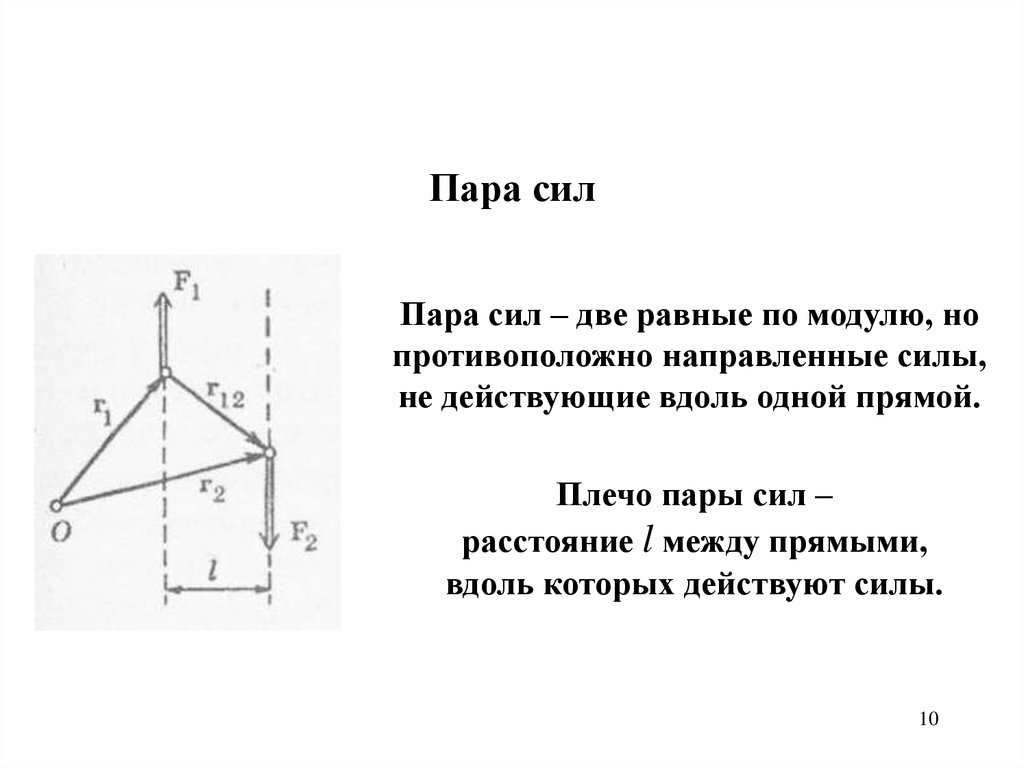
Пара сил
Пара сил – две равные по модулю, но
противоположно направленные силы,
не действующие вдоль одной прямой.
Плечо пары сил –
расстояние l между прямыми,
вдоль которых действуют силы.
10

11.

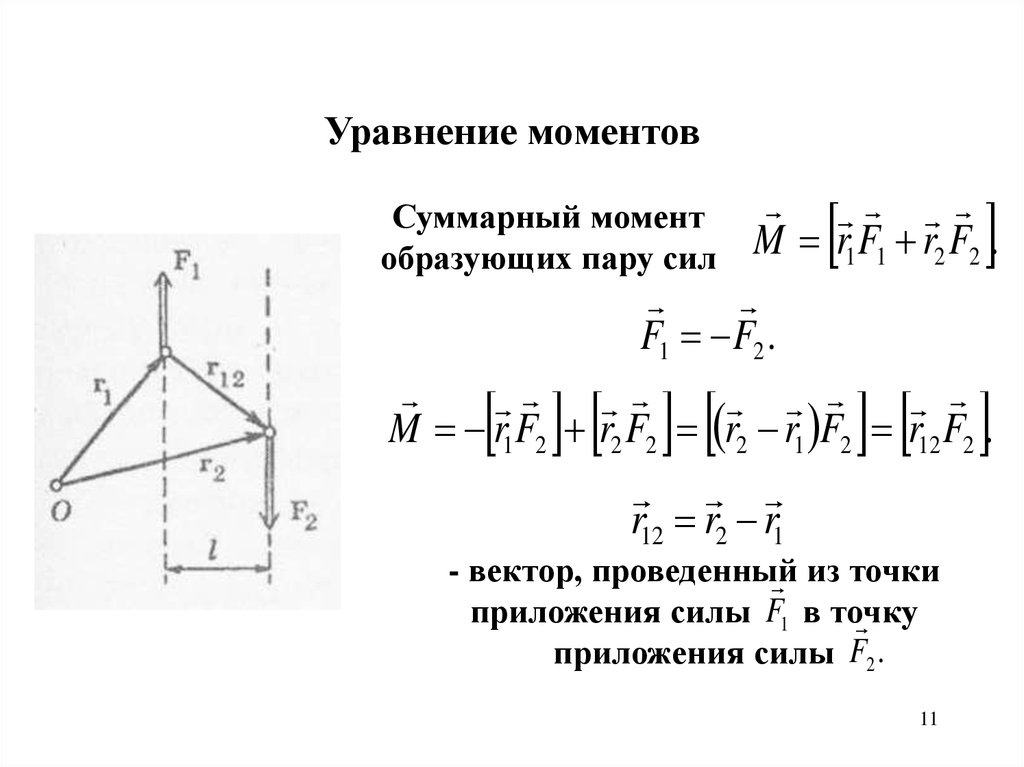
Уравнение моментов
M r1 F1 r2 F2 .
F1 F2 .
M r1F2 r2 F2 r2 r1 F2 r12 F2 .
r12 r2 r1
Суммарный момент
образующих пару сил
- вектор, проведенный
из точки
приложения силы F1 в точку
приложения силы F2 .
11

12.

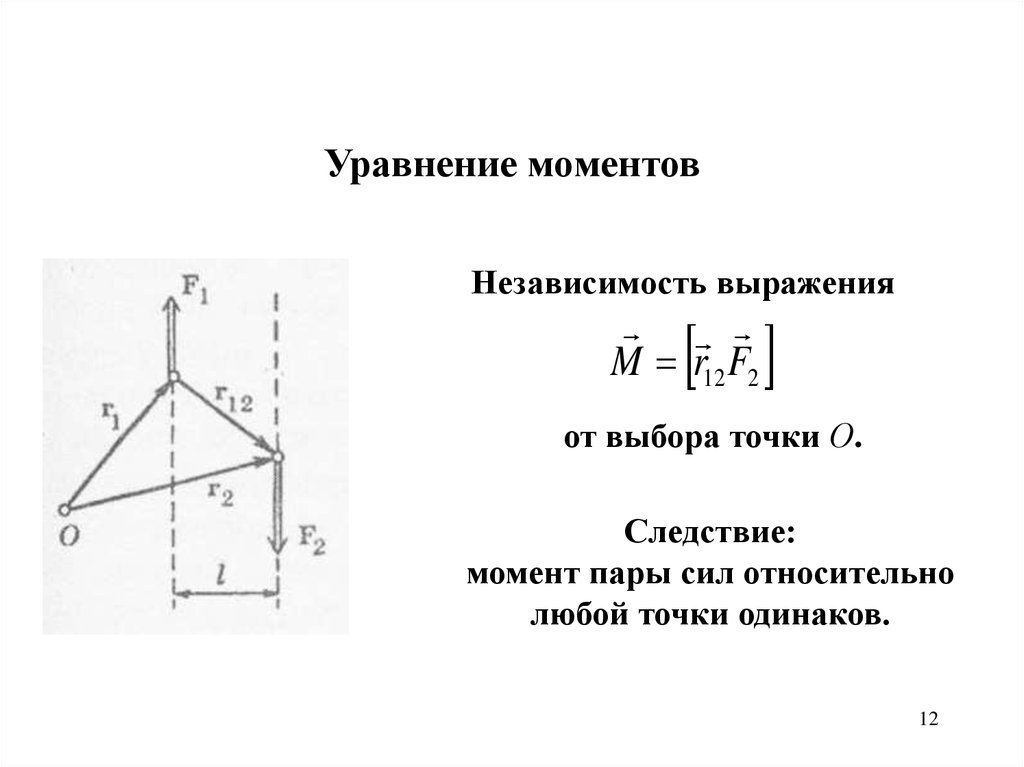
Уравнение моментов
Независимость выражения
M r12 F2
от выбора точки О.
Следствие:
момент пары сил относительно
любой точки одинаков.
12

13.

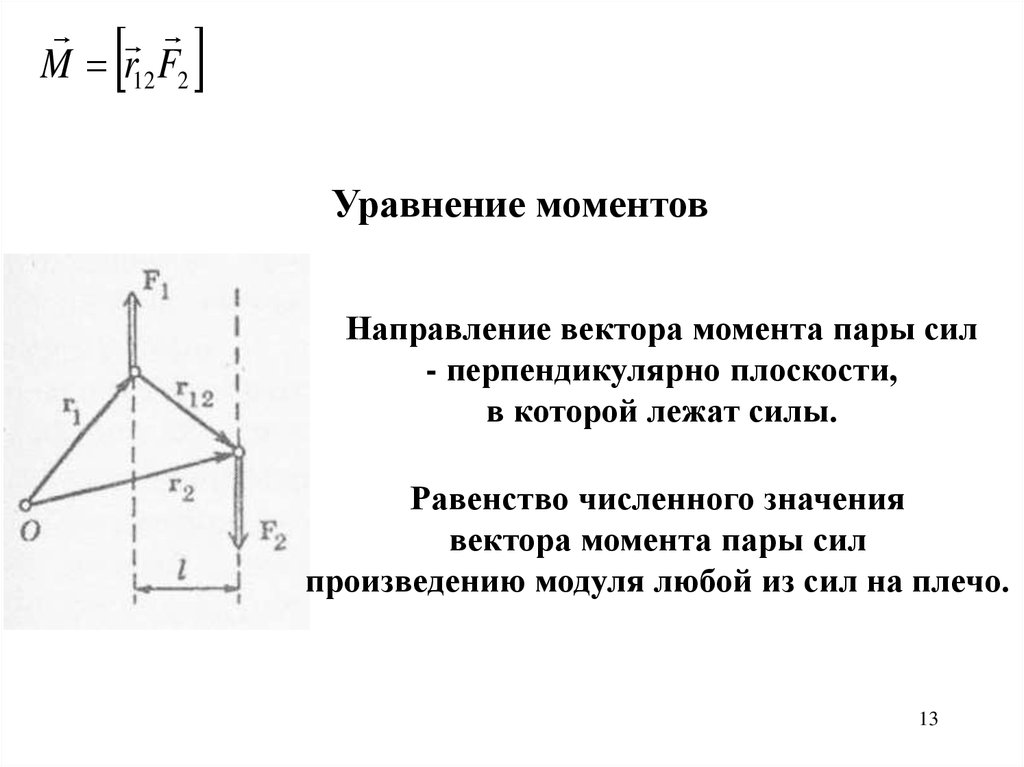
M r12 F2
Уравнение моментов
Направление вектора момента пары сил
- перпендикулярно плоскости,
в которой лежат силы.
Равенство численного значения
вектора момента пары сил
произведению модуля любой из сил на плечо.
13

14.

Уравнение моментов
Действие сил взаимодействия между
частицами вдоль одной и той же прямой.
Равенство по модулю и противоположное
направление вдоль одной и той же прямой
моментов сил взаимодействия
относительно произвольной точки О.
Уравновешивание моментов
внутренних сил друг другом,
в частности, для твердого тела
M внутр 0.
14

15.

Момент инерции
Абсолютно твердое тело – система частиц (материальных
точек) с неизменным расстоянием между ними.
Момент инерции тела относительно некоторой оси –
величина, равная сумме произведений элементарных масс,
из которых состоит данное тело,
на квадраты их расстояний от некоторой оси,
I m R .
2
i i
Равенство момента инерции тела
сумме моментов инерции его частей.
15

16.

Момент инерции
Плотность однородного тела –
характеристика распределения массы m в его объеме V,
m /V .
Плотность неоднородного тела
m dm
lim
.
V 0 V
dV
16

17.

I mi Ri2 .
Момент инерции
mi i Vi .
I i Ri2 Vi .
Если = соnst, то
Наиболее точное решение -
I R Vi .
2
i
I R 2 dm R 2 dV .
17

18.

Теорема Штейнера
Момент инерции I тела относительно произвольной оси
равен сумме моментов инерции IC данного тела
относительно оси, параллельной данной и проходящей
через центр масс тела, и произведения массы тела m на
квадрат расстояния а между осями:
I I C ma 2 .
18

19.

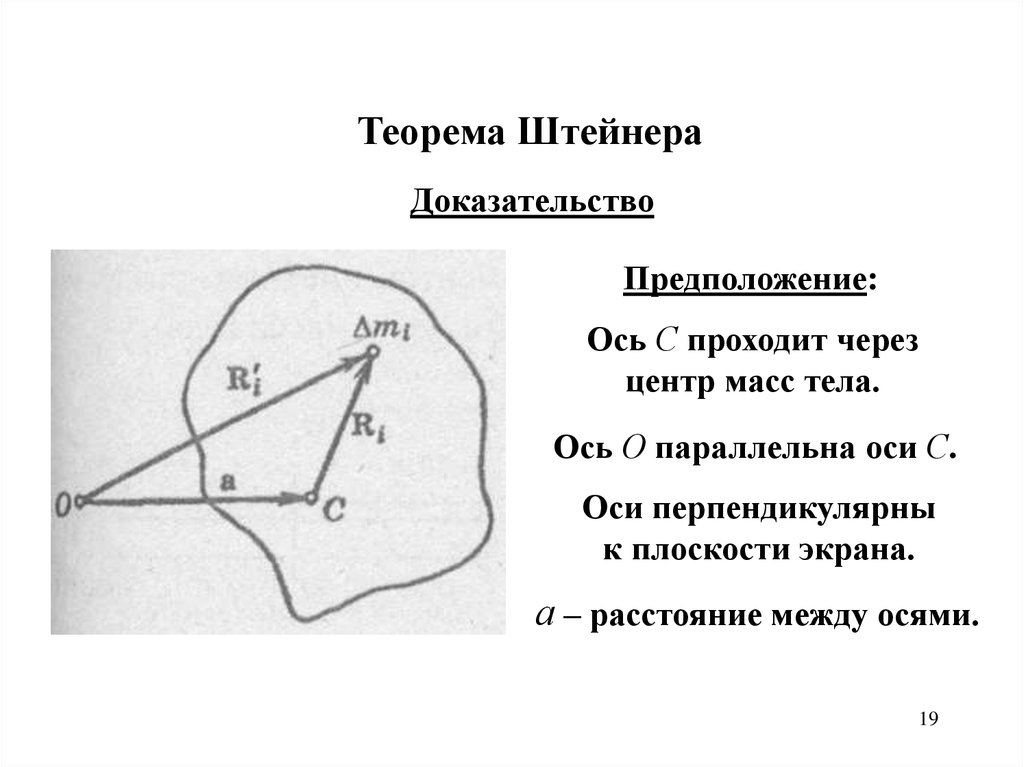
Теорема Штейнера
Доказательство
Предположение:
Ось С проходит через
центр масс тела.
Ось О параллельна оси С.
Оси перпендикулярны
к плоскости экрана.
а – расстояние между осями.
19

20.

Теорема Штейнера
Ri a Ri
2 2
2
Ri a Ri a 2aRi Ri
2
I mi Ri a mi 2a mi Ri mi Ri2
2
2a mi Ri 0
2
- ось С проходит через центр масс.
I ma I C
2
20

21.

Кинетическая энергия
вращательного движения твердого тела
Вращение тела вокруг
неподвижной оси z.
Кинетическая энергия i-й
элементарной массы
2
i i
mv 1
Ti
mi 2 Ri2 .
2
2
Кинетическая энергия тела
вращающегося вокруг неподвижной оси
1 2
T Ti mi Ri2 I 2 / 2.
2
21

22.

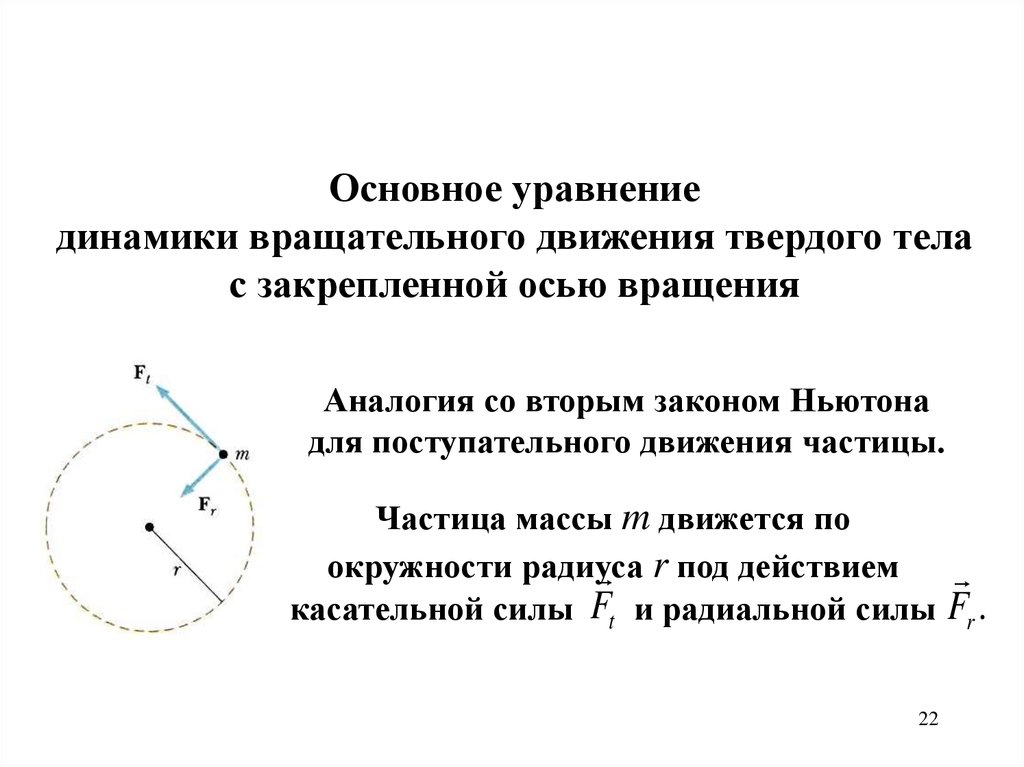
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Аналогия со вторым законом Ньютона
для поступательного движения частицы.
Частица массы m движется по
окружности радиуса
r под действием
касательной силы Ft и радиальной силы Fr .
22

23.

Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
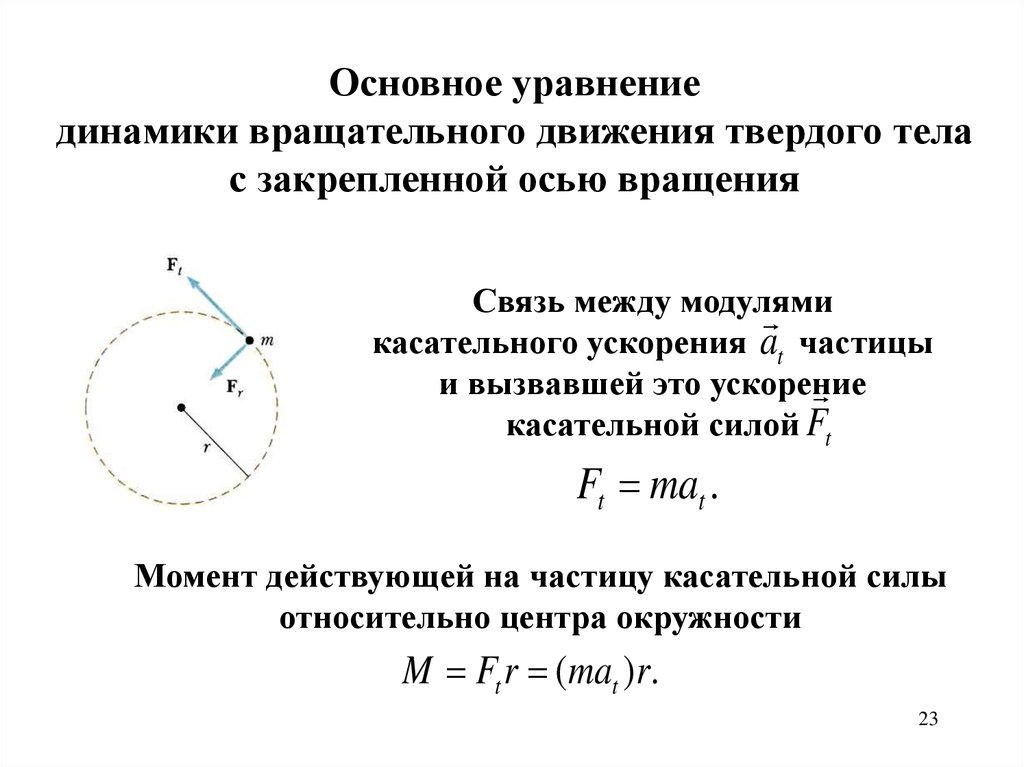
Связь между модулями
касательного ускорения at частицы
и вызвавшей это ускорение
касательной силой Ft
Ft mat .
Момент действующей на частицу касательной силы
относительно центра окружности
M Ft r (mat )r.
23

24.

M Ft r (mat )r.
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Связь между модулями касательного
ускорения и углового ускорения
at r .
Момент действующей на частицу касательной силы
относительно центра окружности
M Ft r mat r (mr )r (mr 2 ) I .
I mr 2 - момент инерции частицы относительно
оси z, проходящей через центр окружности.
24

25.

Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Момент действующей на частицу касательной силы
относительно центра окружности
прямо пропорционален ее угловому ускорению
M I .
25

26.

Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
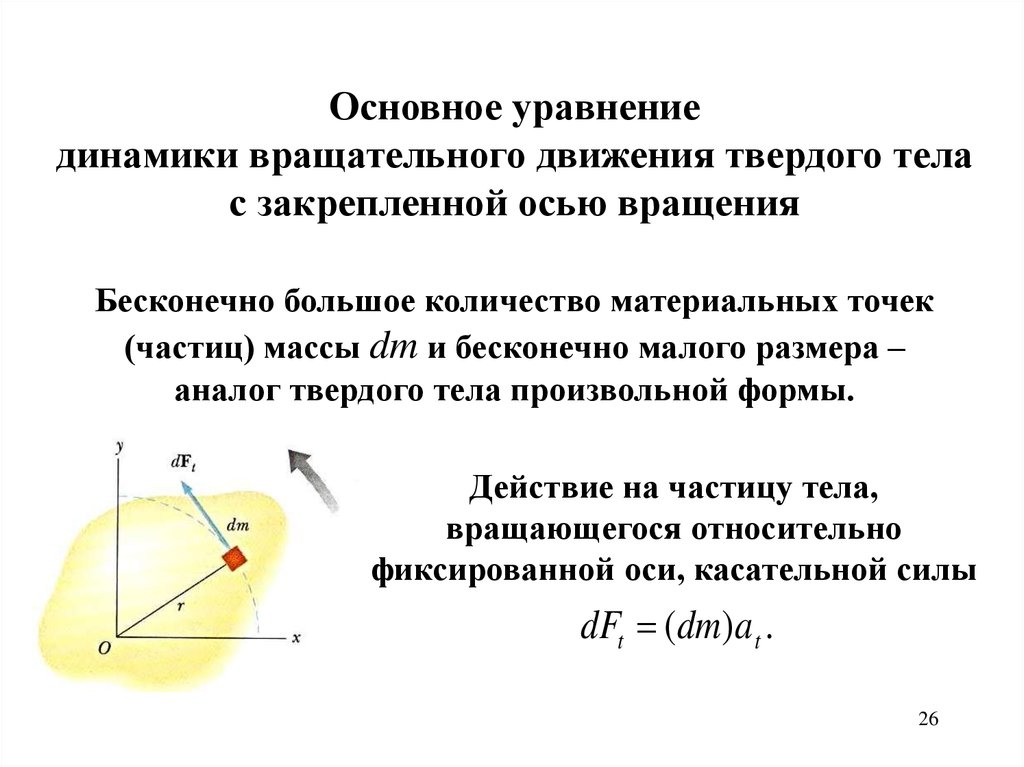
Бесконечно большое количество материальных точек
(частиц) массы dm и бесконечно малого размера –
аналог твердого тела произвольной формы.
Действие на частицу тела,
вращающегося относительно
фиксированной оси, касательной силы
dFt (dm)a t .
26

27.

Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Момент касательной силы, действующий относительно оси
вращения и связанный с касательной силой dFt ,
dM rdFt a t rdm.
at r
Равенство углового ускорения для всех частиц.
dM r 2 dm.
27

28.

Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Момент касательной силы,
действующий относительно оси вращения на тело в целом,
M r dm r dm.
2
2
Момент инерции тела относительно оси вращения,
проходящей через точку О,
I r 2 dm.
28

29.

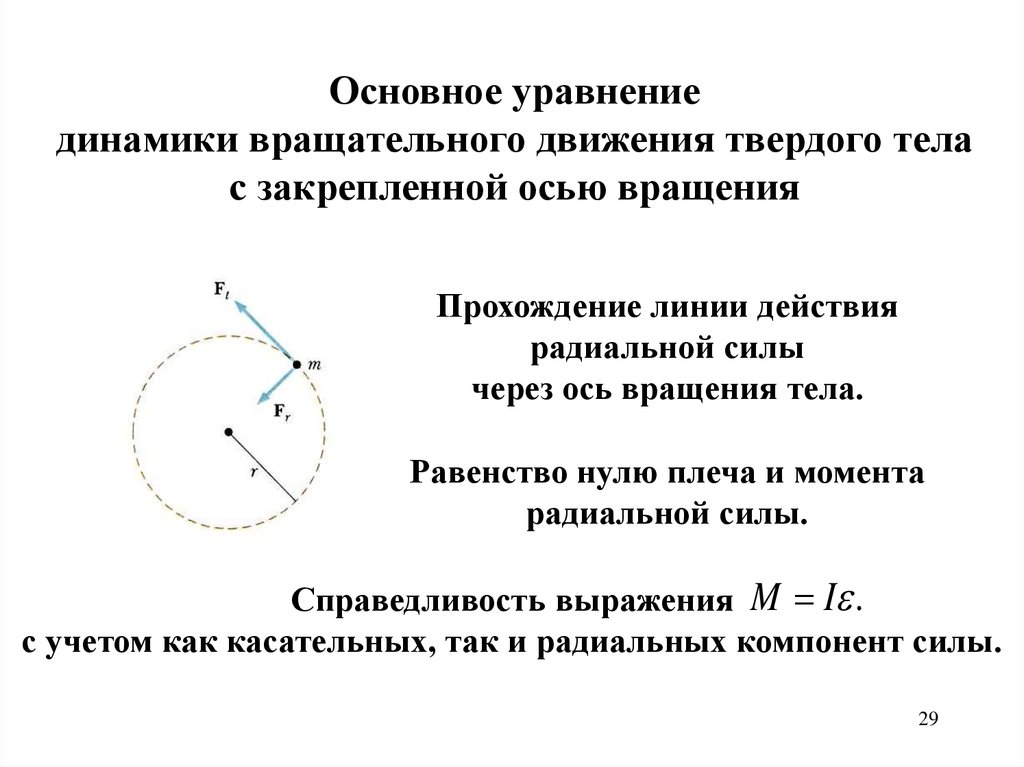
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Прохождение линии действия
радиальной силы
через ось вращения тела.
Равенство нулю плеча и момента
радиальной силы.
Справедливость выражения M I .
с учетом как касательных, так и радиальных компонент силы.
29

30.

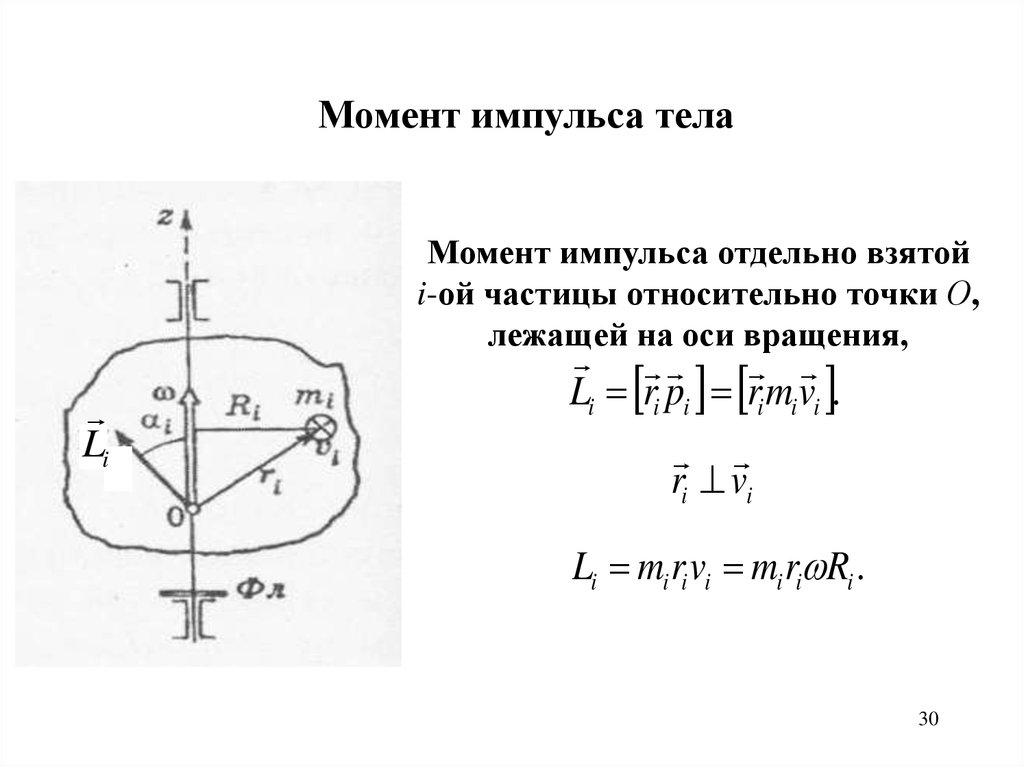
Момент импульса тела
Момент импульса отдельно взятой
i-ой частицы относительно точки О,
лежащей на оси вращения,
Li
Li ri pi ri mi vi .
ri vi
Li mi ri vi mi ri Ri .
30

31.

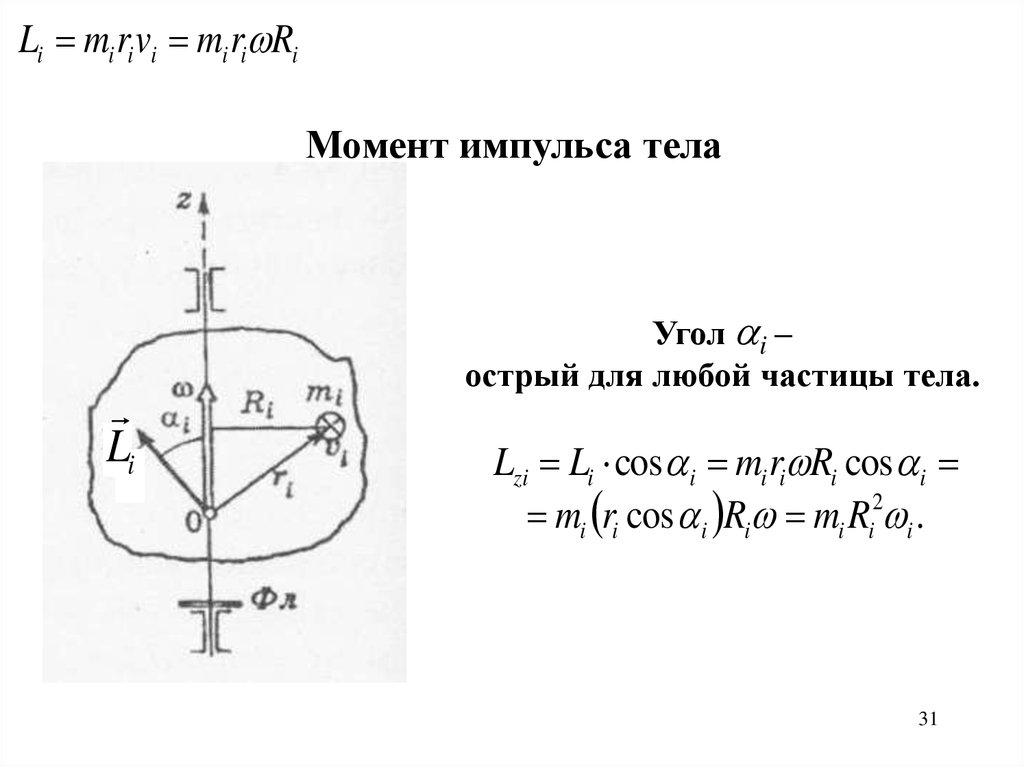
Li mi ri vi mi ri Ri
Момент импульса тела
Li
Угол i –
острый для любой частицы тела.
Lzi Li cos i mi ri Ri cos i
mi ri cos i Ri mi Ri2 i .
31

32.

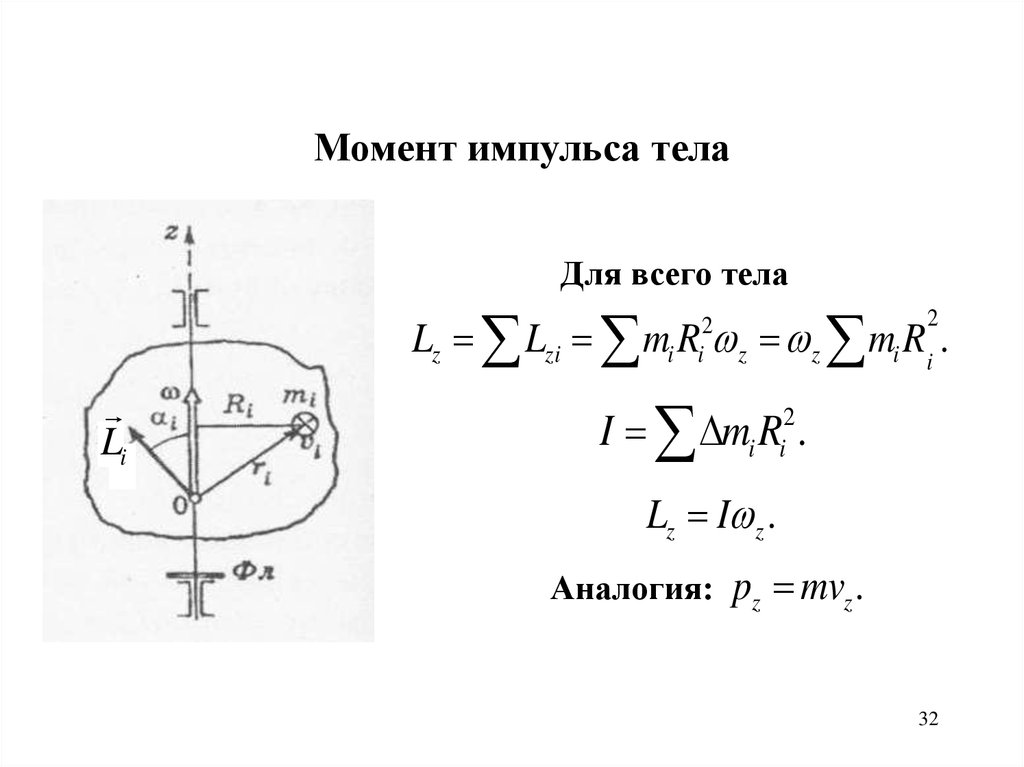
Момент импульса тела
Для всего тела
Lz Lzi m R z z mi Ri .
2
2
i i
Li
I m R .
2
i i
Lz I z .
Аналогия:
pz mvz .
32

33.

Закон сохранения момента импульса
M M i ri Fi
i
i
L Li ri pi
i
i
M внутр 0
Для всякой системы частиц (тела)
d
L M внешн .
dt
33

34.

d
L M внешн .
dt
Lz I z .
Закон сохранения момента импульса
d
Lz M z внешн
dt
z
I z M z внешн
- проекция углового ускорения на ось z.
Аналогия:
m z Fz .
34

35.

Закон сохранения момента импульса
Однородное тело, симметричное относительно оси вращения,
- совпадение по направлению момента импульса
относительно точки О, лежащей
на оси вращения,
и вектора .
L I .
Общий случай несимметричного тела невыполнение данного уравнения.
35

36.

Закон сохранения момента импульса
d
L M внешн .
dt
Если M внешн 0,
d
L 0 и L постоянен.
то
dt
Постоянство во времени момента импульса
замкнутой системы материальных точек.
36

37.

Закон сохранения момента импульса
d
Lz M z внешн
dt
Если
M
z внешн
d
0, то Lz 0 и Lz постоянна.
dt
Постоянство во времени проекции момента импульса
замкнутой системы материальных точек на некоторую ось.
37

38.

Контрольный вопрос
Труба и цилиндр, обладающие
одинаковыми радиусами, массой и длиной (высотой),
вращаются относительно их продольных центральных осей
с одинаковой угловой скоростью.
Большей вращательной кинетической энергией обладает:
а) полая труба,
б) сплошной цилиндр,
в) они обладают одинаковыми значениями
вращательной кинетической энергии,
г) невозможно определить.
38