Гироскопические силы. Гироскопы и их применение в технике. Релятивистская механика. (Лекция 6)

1. Лекция 6

1

2.

Контрольный вопрос
Труба и цилиндр, обладающие
одинаковыми радиусами, массой и длиной (высотой),
вращаются относительно их продольных центральных осей
с одинаковой угловой скоростью.
Большей вращательной кинетической энергией обладает:
а) полая труба,
б) сплошной цилиндр,
в) они обладают одинаковыми значениями
вращательной кинетической энергии,
г) невозможно определить.
T I / 2.
2
I R 2 dm.
I труба I цилиндр
а)
2

3.

Содержание предыдущей лекции
Кинематика и динамика вращательного движения
• Момент инерции. Теорема Штейнера.
• Кинетическая энергия вращательного движения твердого тела.
• Основное уравнение динамики вращательного движения
твердого тела с закрепленной осью вращения.
• Момент импульса тела. Закон сохранения момента импульса.
3

4.

Содержание сегодняшней лекции
Кинематика и динамика вращательного движения
• Гироскопические силы. Гироскопы и их применение в технике.
Релятивистская механика
• Постулаты специальной теории относительности (СТО)
Эйнштейна
• Относительность одновременности и преобразования Лоренца.
• Парадоксы релятивистской кинематики: сокращение длины и
замедление времени в движущихся системах отсчета.
• Преобразования скоростей в релятивистской кинематике.
4

5.

Гироскопические силы
Гироскоп (волчок) – массивное симметричное тело,
вращающееся с большой скоростью вокруг оси симметрии.
Неизменность ориентации оси гироскопа в пространстве -
L I .
5

6.

Гироскопические силы
Допущение: действие пары сил F1 и F2 .
dL
L
M
L
Направление момента M сил F1 и F2
– вдоль прямой О О .
Ожидаемый поворот оси
гироскопа в пространстве
вокруг оси О О .
6

7.

dL
L
L
Гироскопические силы
M
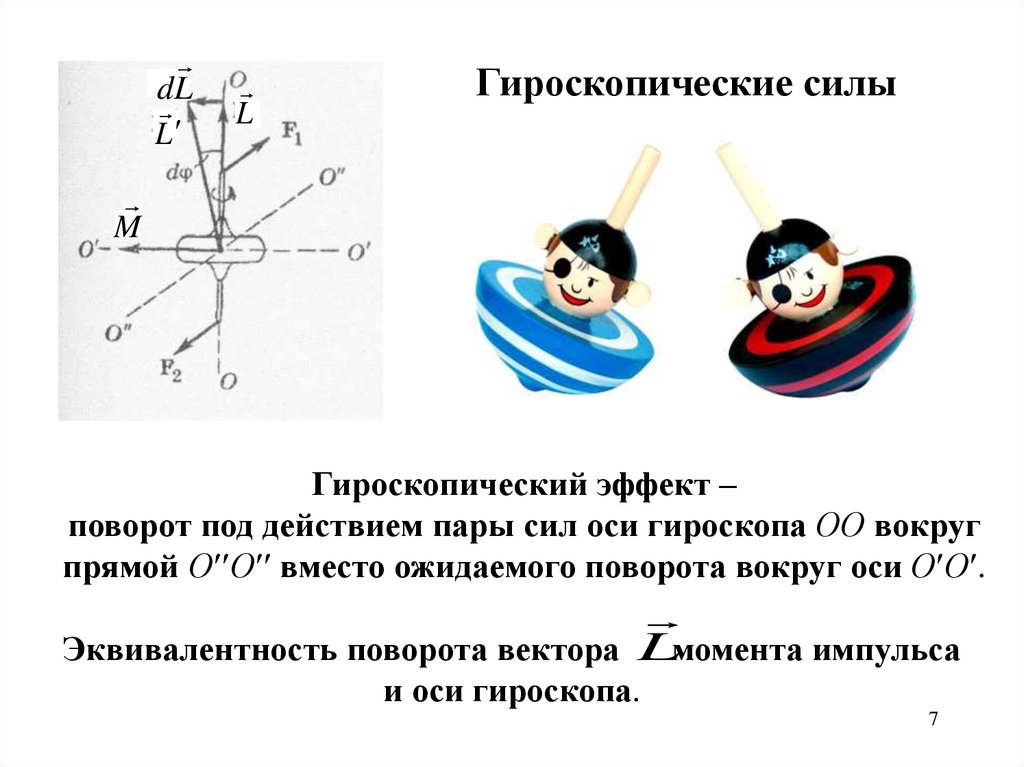
Гироскопический эффект –
поворот под действием пары сил оси гироскопа ОО вокруг
прямой О О вместо ожидаемого поворота вокруг оси О О .
Эквивалентность поворота вектора Lмомента импульса
и оси гироскопа.
7

8.

d
L M внешн
dt
Гироскопические силы
dL
L
M
L
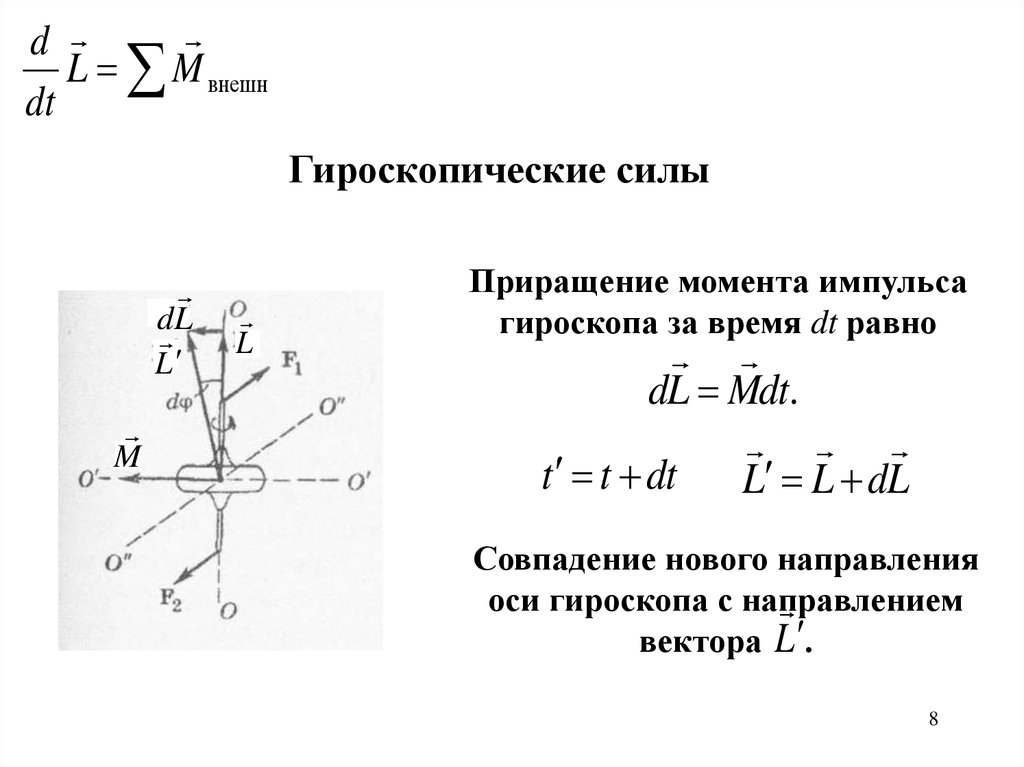
Приращение момента импульса
гироскопа за время dt равно
dL Mdt.
t t dt L L dL
Совпадение нового направления
оси гироскопа с направлением
вектора L .
8

9.

Гироскопические силы
dL
L
L
Поворот оси гироскопа вокруг
прямой О О на угол
d dL / L Mdt / L.
M
Угловая скорость поворота
'' d / dt M / L.
Обратный эффект:
возникновение гироскопических сил,
стремящихся сохранить прежнюю ориентацию,
при попытке вызвать поворот оси гироскопа.
M ''L.
M "L .
9

10. Свойства свободного гироскопа

• сохраняет положение оси вращения в пространстве;
• устойчив к ударным воздействиям;
• обладает необычной реакцией на действие внешней
силы;
• безынерционен.
10

11.

Гироскопы и их применение в технике
гирокомпасы для ручного или
автоматического управления судном,
системы навигации и стабилизации,
системы наведения орудий,
датчики движения,
генераторы момента силы.
11

12.

Релятивистская механика
12

13.

Принцип относительности Галилея
Галилео Галилей
(15 февраля 1564 - 8 января 1642)
итальянский ученый, один из
великих философов нового
времени, основателей точного
естествознания.
• заложил основы классической механики, в частности динамики,
• открыл закон инерции, законы свободного падения, движения тела по
наклонной плоскости и тела, брошенного под углом к горизонту, закон
сложения движений и закон постоянства периода колебаний маятника,
• исследовал прочность материалов,
• создал телескоп с 32-кратным увеличением,
• обнаружил фазы у Венеры, пятна на Солнце, четыре спутника у Юпитера
и горы на Луне.
13

14.

Принцип относительности Галилея
Неизменность уравнений динамики при переходе от
одной инерциальной системы отсчета к другой.
Инвариантность уравнений динамики по отношению к
преобразованию координат, соответствующему переходу
от одной инерциальной системы отсчета к другой.
14

15.

Принцип относительности Галилея
Эквивалентность всех инерциальных систем отсчета.
Невозможность
установления какими-либо механическими опытами,
проведенными в пределах инерциальной системы отсчета,
находится ли она в состоянии покоя или в состоянии
равномерного и прямолинейного движения.
15

16.

Принцип относительности Галилея
Одинаковость законов механики
в различных системах отсчета.
Система отсчета
движущегося грузовика.
Система отсчета
наблюдателя на земле.
Невозможность выявления различий в поведении тел в
различных инерциальных системах отсчета с помощью
экспериментов в рамках механики.
16

17.

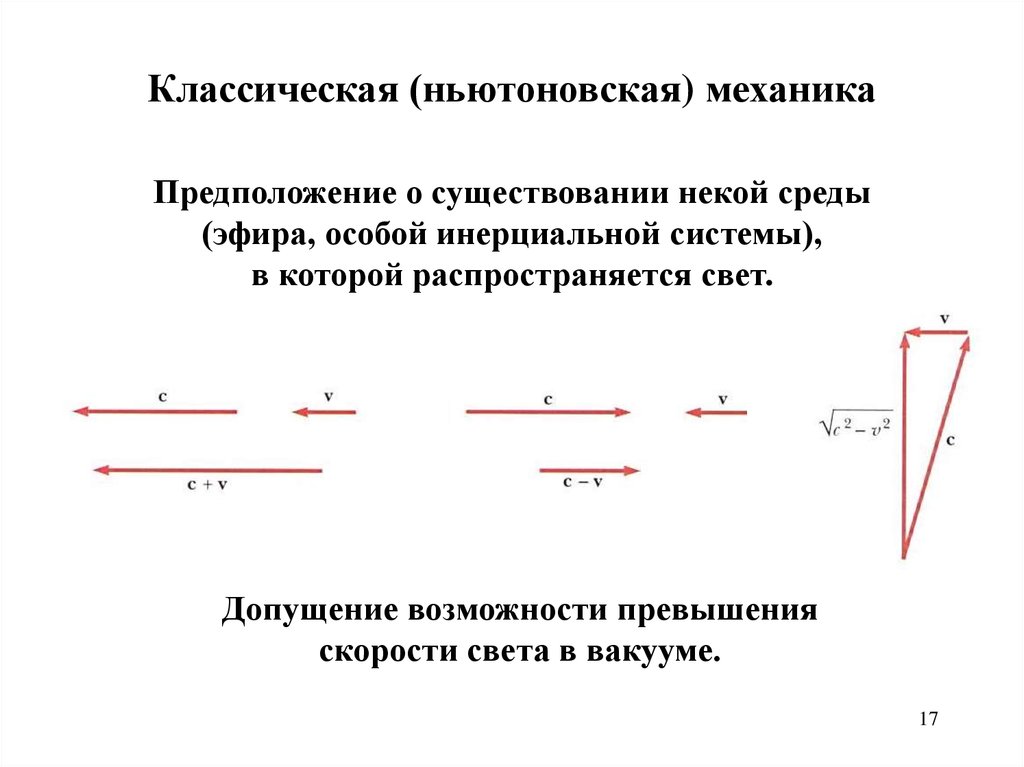
Классическая (ньютоновская) механика
Предположение о существовании некой среды
(эфира, особой инерциальной системы),
в которой распространяется свет.
Допущение возможности превышения
скорости света в вакууме.
17

18.

Постулаты специальной теории
относительности (СТО) Эйнштейна
Опыт Майкельсона-Морли
Отсутствие специальной инерциальной системы отсчета
(эфира) – независимость скорости света от скорости и
направления движения источника света.
18

19.

Постулаты специальной теории
относительности (СТО) Эйнштейна
Принцип относительности Эйнштейна:
все законы природы одинаковы
во всех инерциальных системах отсчета,
уравнения, выражающие законы природы,
инвариантны по отношению к преобразованию координат и
времени от одной инерциальной системы отсчета к другой.
19

20.

Постулаты специальной теории
относительности (СТО) Эйнштейна
Принцип постоянства скорости:
Скорость света в вакууме одинакова и равна c = 3,00 108 м/c
во всех инерциальных системах отсчета независимо от
скорости наблюдателя или скорости источника света.
20

21.

Промежуток времени между событиями
Следствие постоянства скорости света в вакууме и ее
независимости от движения источников света –
относительность понятия одновременности событий.
Взаимосвязь пространства и времени
с образованием единого пространства-времени.
21

22.

Промежуток времени между событиями
Система отсчета, связанная с движущимся вагоном, наблюдатель в точке О .
Зеркало
Событие 1 - вспышка света в точке О ,
событие 2 - возвращение вспышки
света после отражения от зеркала
к наблюдателю в ту же точку О .
Происхождение событий
в одной и той же точке пространства
движущегося вагона.
22

23.

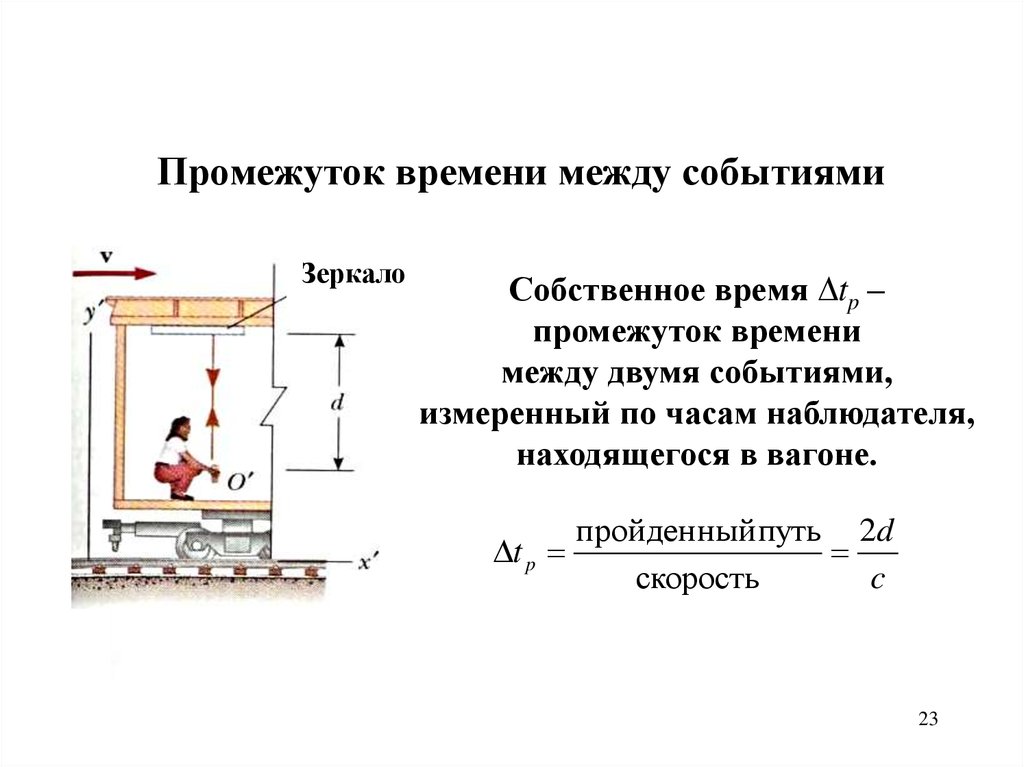
Промежуток времени между событиями
Зеркало
Собственное время tp –
промежуток времени
между двумя событиями,
измеренный по часам наблюдателя,
находящегося в вагоне.
t p
пройденный путь 2d
скорость
c
23

24.

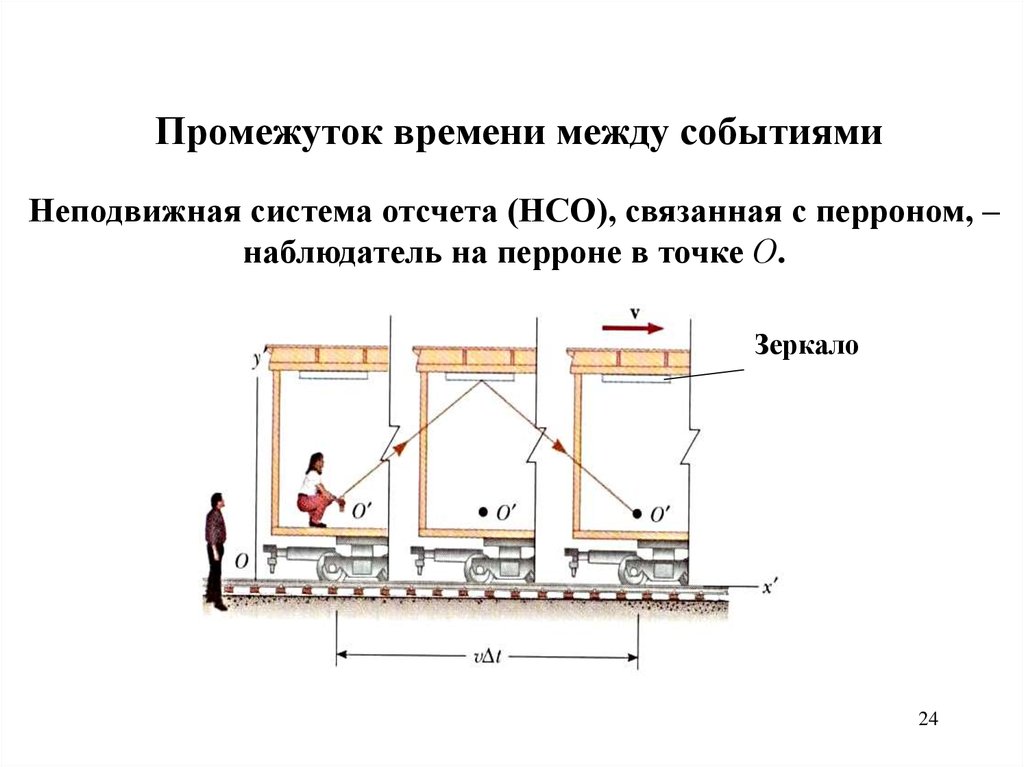
Промежуток времени между событиями
Неподвижная система отсчета (НСО), связанная с перроном, –
наблюдатель на перроне в точке О.
Зеркало
24

25.

Промежуток времени между событиями
Система отсчета, связанная с вагоном, движущаяся система отсчета по отношению к событиям,
происходящим в НСО, связанной с перроном.
Зеркало
Событие 1 - вспышка света в вагоне,
событие 2 - попадание вспышки света после отражения от
зеркала в ту же точку вагона, сместившуюся на v t по
отношению к наблюдателю на перроне.

26.

Промежуток времени между событиями
2
2
c t v t
2
d
2 2
t
2d
c v
2
2
2d
v2
c 1 2
c
- промежуток времени,
измеренный по часам наблюдателя, находящегося на перроне.
26

27.

Промежуток времени между событиями
t
t p
1
2
v
c2
t p
1
1
2
1
(v c )
v
c2
t t p
Различие во временных интервалах
между одинаковыми событиями, происходящими
в движущейся (вагон) и неподвижной (перрон) СО.
Часы в движущейся СО отсчета кликают реже,
чем в неподвижной, - эффект сжатия времени.
27

28.

Промежуток времени между событиями
Значимость эффекта сжатия времени
только для больших скоростей
γ
v, 108 м/с
28

29.

Промежуток времени между событиями
Доля нераспавшихся мюонов
Сжатие времени –
возможность мюонам (элементарным частицам в
космических лучах) достичь поверхности Земли.
Мюоны, движущиеся
со скоростью 0,9994 с
Мюоны
в покое
Время жизни, сек
29

30.

Промежуток времени между событиями
Парадокс близнецов
До полета
После полета
Необходимость учета того, что лишь близнец на Земле
находился в инерциальной системе отсчета.
30

31.

Сокращение длины в движущихся системах отсчета
Наблюдатель на Земле
(неподвижный по отношению к звездам):
Lp – расстояние между двумя звездами (собственное
расстояние, т.к. измеряется в покоящейся системе отсчета),
v – скорость космического корабля,
t = Lp / v – время, необходимое для преодоления
расстояния между звездами, измеренное по часам
наблюдателя на Земле.
31

32.

Сокращение длины в движущихся системах отсчета
Космонавт, летящий от одной звезды к другой:
tp = t /γ – время, необходимое для преодоления расстояния
между звездами, с точки зрения космонавта.
Измерение промежутка времени tp полета между звездами
в одной и той же точке движущейся системы отсчета (ракете).
L= v tp – расстояние между двумя звездами, измеренное
в движущейся системе отсчета (космонавтом в ракете).
L v
t
Lp
Lp
v2
1 2
c
32

33.

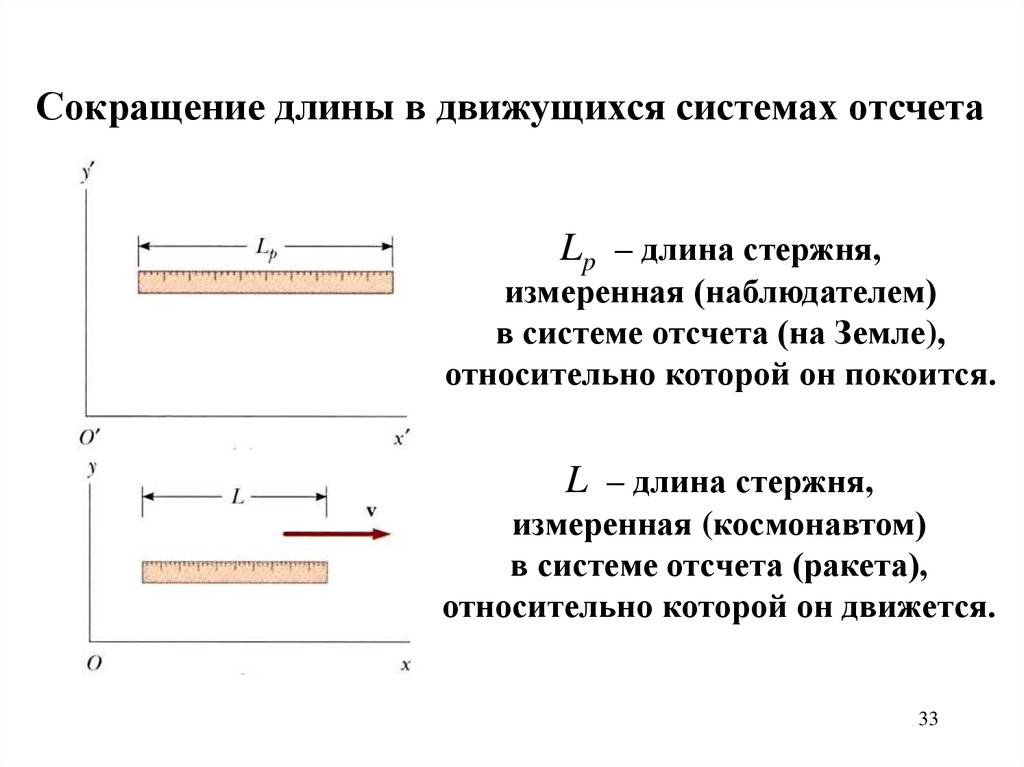
Сокращение длины в движущихся системах отсчета
Lp – длина стержня,
измеренная (наблюдателем)
в системе отсчета (на Земле),
относительно которой он покоится.
L – длина стержня,
измеренная (космонавтом)
в системе отсчета (ракета),
относительно которой он движется.
33

34.

Сокращение длины в движущихся системах отсчета
L Lp
v2
1 2
c
v2
1 2 1
c
L Lp
НСО: сокращение длины
движущегося объекта по
сравнению с его длиной в
состоянии покоя.
Изменение размеров тела –
только в направлении движения.
34

35.

Преобразования систем координат
Координаты события в точке P:
для наблюдателя в системе отсчета S – (x, y, z, t),
для наблюдателя в системе отсчета S – (x , y , z , t ).
Событие Р
Событие Q
35

36.

Преобразования Галилея
События P и Q:
согласно преобразованиям Галилея x = x независимость расстояния между двумя точками
от того движется наблюдатель или нет.
Событие Р Событие Q
Эксперимент: несправедливость преобразований Галилея
при скоростях, близких к с, –
движение приводит к сокращению длины.
36

37.

Преобразования Лоренца
Уравнения преобразований Лоренца,
справедливые для всех скоростей
S S
v
x x vt y y z z t t 2
c
S S
v
x x vt y y z z t t 2
c
x
x
v << c – получение уравнений Галилея из уравнений Лоренца
S S
x x vt
y y
z z
t t
37

38.

x x vt
v
t t 2 x
c
Преобразования Лоренца
Расстояние между событиями
x x v t
v
t t 2 x
c
S S
x x v t
v
t t 2 x
c
S S
x x2 x1 , t t2 t1 - измерения наблюдателем в СО S
x x2 x1 , t t2 t1 - измерения наблюдателем в СО S
38

39.

Преобразования Лоренца
Преобразование скоростей
Движение двух наблюдателей друг относительно друга
и отслеживание одного и то же события
(движения одного и того же объекта).
Малые скорости: преобразования Галилея
u x u x v
Большие скорости: преобразования Лоренца
???
39

40.

Преобразования Лоренца
Преобразование скоростей
Движение системы отсчета S
по отношению к системе отсчета S
со скоростью v в положительном направлении оси x.
Уравнения Лоренца:
x x vt
v
t t 2 x
c
Результат дифференцирования уравнений Лоренца:
dx dx vdt
v
dt dt 2 dx
c
40

41.

Преобразования Лоренца
Преобразование скоростей
dx
v
dx
dx vdt
u x
dt
dt dt v dx 1 v dx
2
2
c
c dt
uy
uz
ux v
u z
u y
u x
uxv
uxv
uxv
1 2
1 2
1 2
c
c
c
41

42.

Преобразования Лоренца
Преобразование скоростей
ux v
u x
uxv
1 2
c
u x u x v (преобразование Галилея)
S S
v c
42

43.

ux v
u x
uxv
1 2
c
Преобразования Лоренца
Преобразование скоростей
Независимость скорости распространения света
от скорости движения системы отсчета
ux c
v
c 1
c v
c
ux
c
cv
v
1 2
1
c
c
43

44.

S S
ux v
u x
uv
1 x2
c
Преобразования Лоренца
Преобразование скоростей
v v
S S
u x u x
u x v
ux
u x v
1 2
c
44

45.

Контрольный вопрос
Команда космического корабля смотрит 2-часовой
фильм на борту корабля.
Для наблюдателя на Земле, смотрящего тот же фильм
с помощью телескопа через иллюминатор корабля,
продолжительность фильма:
а) > 2 часов, б) < 2 часов, в) = 2 часам.
45