Похожие презентации:
Нелінійна динаміка трубопроводу з рідиною в околі критичних швидкостей течії рідини
1.
МІЖНАРОДНИЙ МАТЕМАТИЧНИЙ ЦЕНТР ІМЕНІ Ю.О. МИТРОПОЛЬСЬКОГОНАН УКРАЇНИ
ТІМОХІН ОЛЕКСІЙ ПАВЛОВИЧ
НЕЛІНІЙНА ДИНАМІКА ТРУБОПРОВОДУ З
РІДИНОЮ В ОКОЛІ КРИТИЧНИХ ШВИДКОСТЕЙ
ТЕЧІЇ РІДИНИ
Спеціальність: 01.02.01 – теоретична механіка
Дисертація на здобуття наукового ступеня
кандидата фізико-математичних наук
КИЇВ – 2015
2.
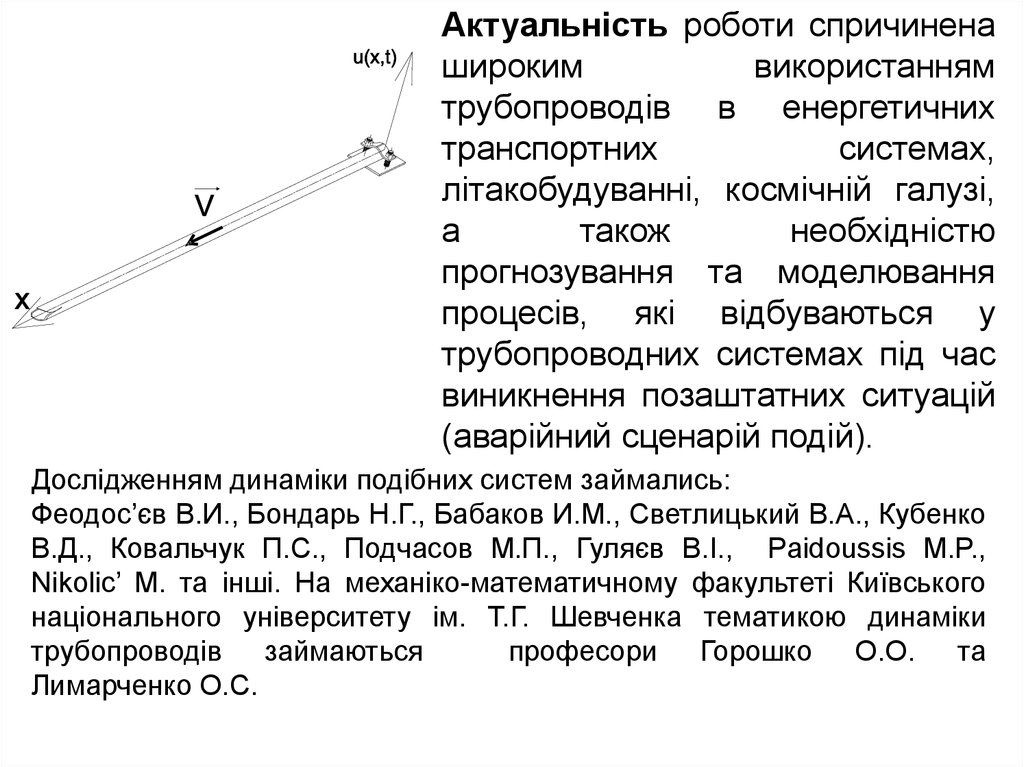
Актуальність роботи спричиненашироким
використанням
трубопроводів в енергетичних
транспортних
системах,
літакобудуванні, космічній галузі,
а
також
необхідністю
прогнозування та моделювання
процесів, які відбуваються у
трубопроводних системах під час
виникнення позаштатних ситуацій
(аварійний сценарій подій).
Дослідженням динаміки подібних систем займались:
Феодос’єв В.И., Бондарь Н.Г., Бабаков И.М., Светлицький В.А., Кубенко
В.Д., Ковальчук П.С., Подчасов М.П., Гуляєв В.І., Paidoussis M.P.,
Nikolic’ M. та інші. На механіко-математичному факультеті Київського
національного університету ім. Т.Г. Шевченка тематикою динаміки
трубопроводів займаються
професори Горошко О.О. та
Лимарченко О.С.
3.
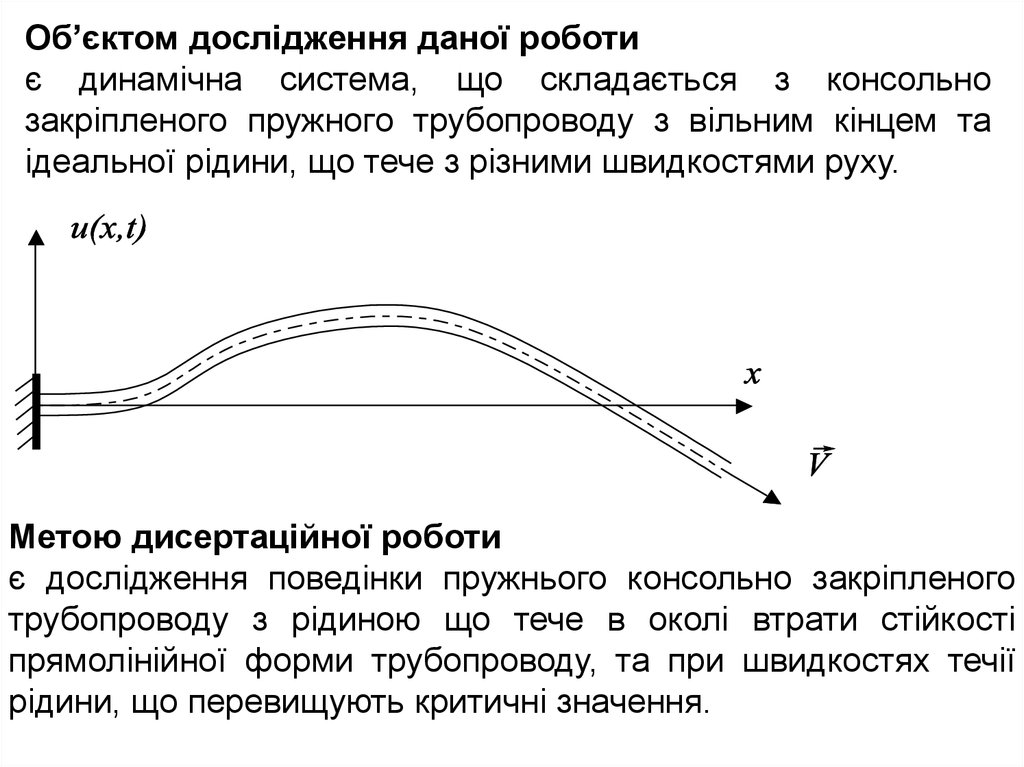
Об’єктом дослідження даної роботиє динамічна система, що складається з консольно
закріпленого пружного трубопроводу з вільним кінцем та
ідеальної рідини, що тече з різними швидкостями руху.
Метою дисертаційної роботи
є дослідження поведінки пружнього консольно закріпленого
трубопроводу з рідиною що тече в околі втрати стійкості
прямолінійної форми трубопроводу, та при швидкостях течії
рідини, що перевищують критичні значення.
4.
Предметом дослідження роботи є нелінійні динамічніпроцеси в системі трубопровід – рідина, які відбуваються в
околі втрати стійкості прямолінійної форми рівноваги
трубопроводу, та при швидкостях течії рідини, що
перевищують критичні значення.
Методи дослідження.
• Методи нелінійної механіки та математичної фізики
• Варіаційне формулювання на основі принципу Гамільтона–
Остроградського
• Метод модальної декомпозиції (метод Канторовича)
• Дослідження стійкості системи на основі першого методу
Ляпунова
• Методи символьних аналітичних перетворень, числові методи
та методи графічної візуалізації даних, реалізовані у пакеті
Mathematica 8
5.
Наукова новизна отриманих результатів полягає у тому, що:• Засобами символьної математики побудована модель нелінійної
динаміки пружного трубопроводу з рідиною, що тече.
• Вперше
аналітично
досліджена
проблема
втрати
стійкості
прямолінійної форми трубопроводу на основі чотирьохмодової моделі
динамічної системи.
• Досліджено специфіку прояву сил Коріоліса в докритичному та
закритичному діапазонах швидкостей течії рідини, а також визначені
стани динамічної рівноваги та досліджено розвиток коливань
трубопроводу навколо станів альтернативної рівноваги.
• Здійснено аналітико-чисельну перевірку основних режимів поведінки
трубопроводу з рідиною на основі нелінійної динамічної моделі
системи.
Достовірність отриманих результатів забезпечується:
• Використанням варіаційних алгоритмів для формулювання і
розв’язання задачі
• Використанням засобів символьної математики і адаптивних неявних
методів інтегрування з контролем збіжності реалізованих у пакеті
Mathematica 8, що дозволило побудувати модель великої розмірності.
• Узгодженням частини результатів аналітичних і числових досліджень з
результатами, отриманими іншими авторами.
6.
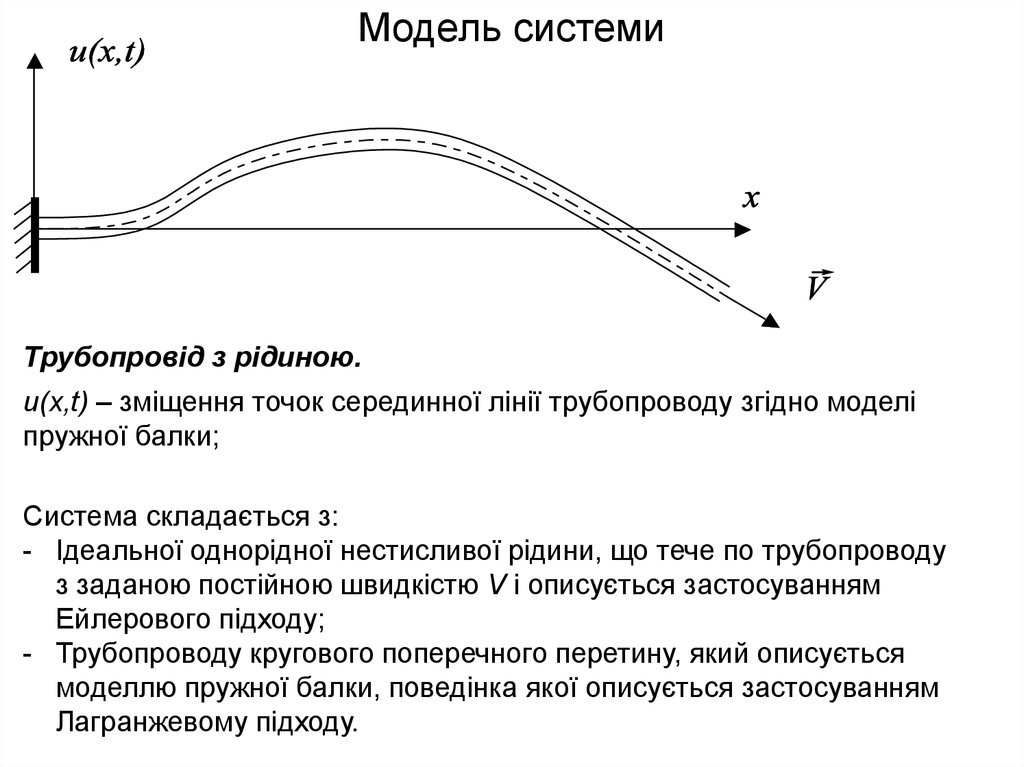
Модель системиТрубопровід з рідиною.
u(x,t) – зміщення точок серединної лінії трубопроводу згідно моделі
пружної балки;
Система складається з:
- Ідеальної однорідної нестисливої рідини, що тече по трубопроводу
з заданою постійною швидкістю V і описується застосуванням
Ейлерового підходу;
- Трубопроводу кругового поперечного перетину, який описується
моделлю пружної балки, поведінка якої описується застосуванням
Лагранжевому підходу.
7.
Складові функції ЛагранжаКінетична енергія балки має такий вигляд
1
u
TB 2
2 o t
l
2
1 u '2 dx
Потенціальна енергія згинних деформацій балки
u
1
П B EJ 2
2
x
o
l
2
2
1 u '2 dx
Потенціальна енергія, що пов’язана з повздовжнім стисканням
матеріалу трубопроводу буде
l
CT
1
EF u 4 dx
8
0
8.
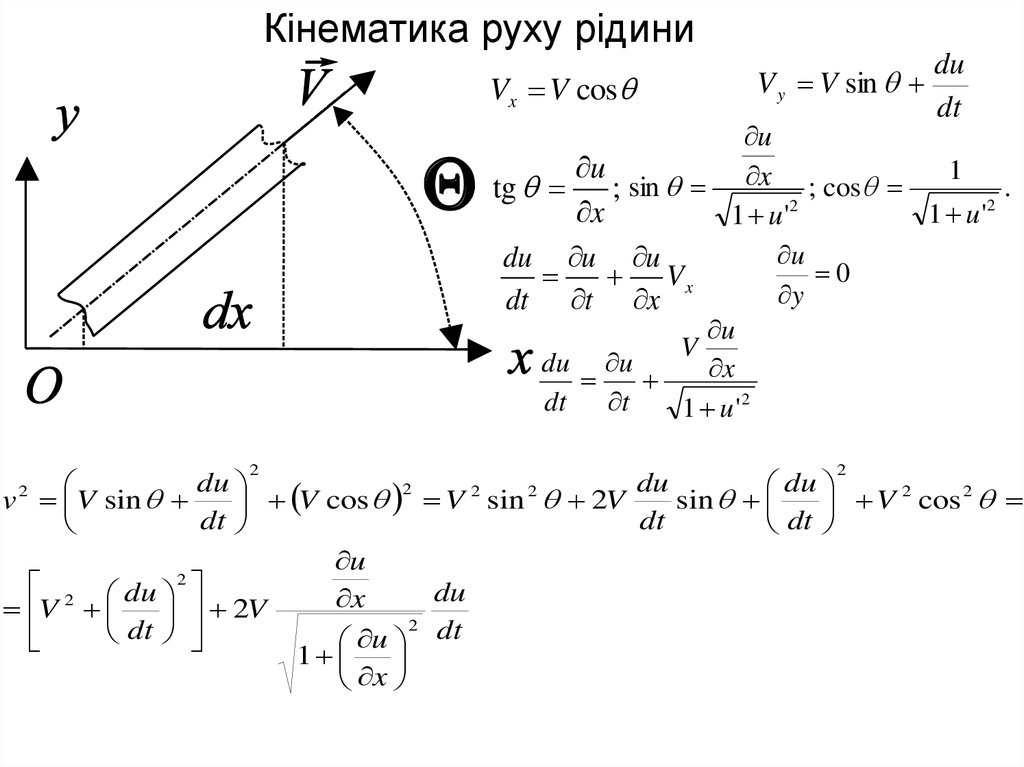
Кінематика руху рідиниVx V cos
V y V sin
du
dt
u
u
1
.
tg ; sin x 2 ; cos
2
x
1 u'
1 u'
u
du u u
0
Vx
y
dt t x
u
V
du u
x
dt
t
1 u'2
2
2
du
du
du
2
2
2
2
2
v 2 V sin
sin
V cos V sin 2V
V cos
dt
dt
dt
u
2
2 du
du
x
V
2
V
2
dt
u
dt
1
x
9.
Кінетична енергія рідини2
1
u
du
2 du
2
V 1 u ' 2V
dx
2 0
x dt
dt
l
T
Ж
Потенціальна енергія рідини, зумовлена внутрішнім тиском
ж
2
1
u
PF2 dx
2
x
0
l
10.
Функція Лагранжа2
u
1 u
1 u u
1
L dx dx EJ 2 dx
2 0 t
4 0 t x
2 0 x
2
l
2
l
2
2
l
2
u u
1
1
1
4
2 u
EJ 2 dx EF u dx V dx
4 0 x x
8
4
x
0
0
l
2
2
l
4
2
l
2
1
1 du
1 du u
2 u
V dx dx dx
16
x
2 0 dt
4 0 dt x
0
l
2
l
2
l
u du
1
1
u
V
dx PF2 dx V 2 dx.
x dt
2
x
2
0
0
0
l
l
2
l
11.
Дискретизація функції ЛагранжаПредставлення функції переміщення точок трубопроводу u(x,t) у вигляді
ряду:
N
A x - форми коливань труби як балки
u ( x, t ) Ai ( x)ci (t )
i 1
ci t
i
- амплітудні параметри, що залежать
від часу.
Для побудови нелінійної дискретної моделі системи треба
обчислити такі квадратури від власних форм коливань труби :
l
l
l
0
0
2
1
A
A
dx
;
N i A dx; ij i j
ij Ai A j dx ;
2
i
0
d
2
ijkl
l
l
0
0
l
4
6
d
A
A
A
A
dx
;
d
Ai Aj Ak Al dx; ijkl
i j k l
ijkl Ai A j Ak Al dx.
0
12.
Функція Лагранжа в амплітудних параметрах1
1
1 EJ
2
2
L1 c i N i c i c j c k c l d ijkl
2 i
4 ijkl
2
1 EJ
4
ci c j c k cl d
ijkl
6
ijkl
1 EF
8
2 4
c
i i Ni
i
4
c
c
c
c
d
i j k l ijkl
ijkl
2
13 V 2
7
V
2 V
4
2
1
c
c
c
c
d
c
c
c
c
i j k l
ijkl
i j ij
i j
ij
16 ijkl
4 ij
ij
1 PF2
2
ci c j ij
2 ij
13.
Рівняння руху системи2
EJ
7
V
c r
r4 cr
2 N r
PF2
N r
c i c j c k
ijk
2 V
2
c
i i ir N
r
2 V
i ci N
r
2
ir
1
i ci 2 N
r
2
ir
1 2
1 2
EJ
d jkir d krij
Nr
2
N r
EF
2 N r
c c c
i
ijk
j
4
d
k ijkr
13
V 2
4 N r
ci
1
ri
i
2
c
c
c
d
i j k jkir
ijk
6
c
c
c
d
i j k ijkl
ijk
c c c
i
ijk
ir1
j
4
d
k ijkr
14.
Зведення системи диференціальних рівнянь доформи, розрішеної відносно старшої похідної,
придатної для чисельного розв’язку
c i в правій частині рівнянь руху
Замість
скористаємось лінійним наближенням:
2
EJ
7
V
c p
p4 c p
2 N p
2 V
N p
ci
2 V
N p
1
pi
i
1
ip
c
i
ip2
i
PF2
N p
2
c
i ip
i
2
c
i ip
i
Лінійне наближення обираємо з міркувань збереження
членів до 3-го порядку малості
15.
Система звичайних диференціальних рівнянь уформі, розрішеній відносно старшої похідної
EJ
7
V 2
4
c r
r cr
2 N r
2 V
N r
ijk
i
ir2
i
PF N c
1
1
c
i ri ir
i
2 V
N r
c i c j ck
c
2
i
4
c
c
c
d
i j k ijkr
ijk
1 2
1 2
EJ
d jkir d krij
Nr
2
N r
EF
2 N r
c c c d
i
7
V 2
2 N p
PF2
N p
j k
ijk
4
ijkr
1
2Nr
c c c d
i
j k
6
ijkl
ijk
EJ
c
c
p4 c p
j k
pjk
2 V
i ci N
p
2
ip
2 V
i ci N
p
2
ip
i
r
2
13
V
2
c
i i ir 4 N
r
2
ir
1
1
c
i pi ip
i
i ci
2
ip
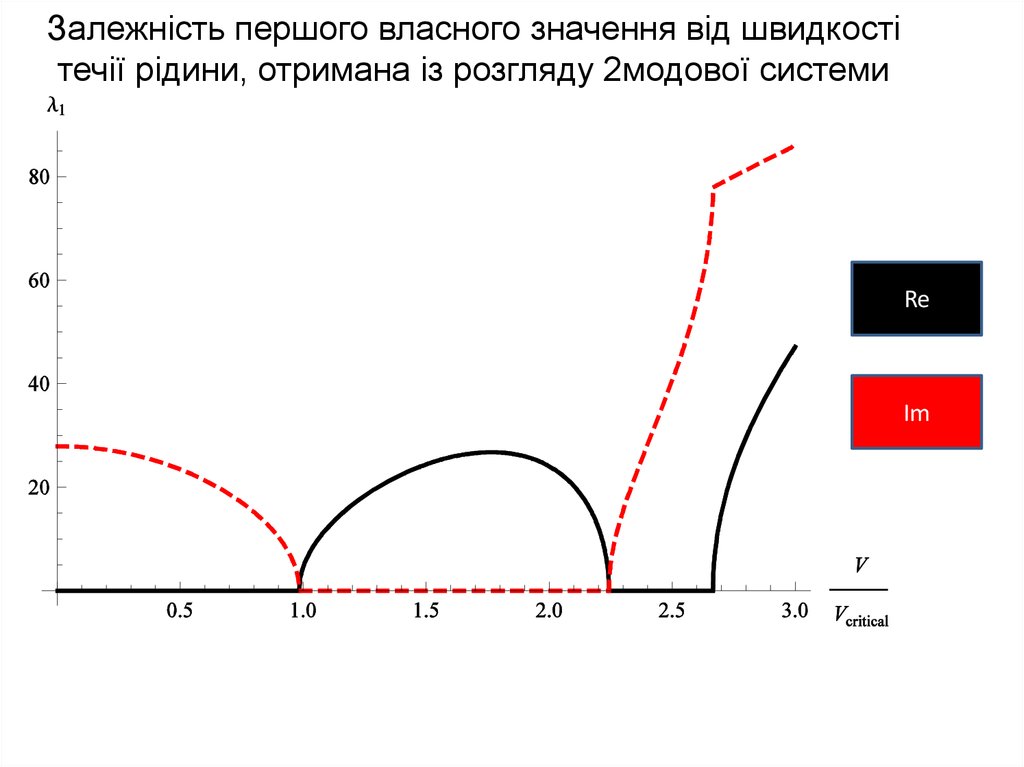
16.
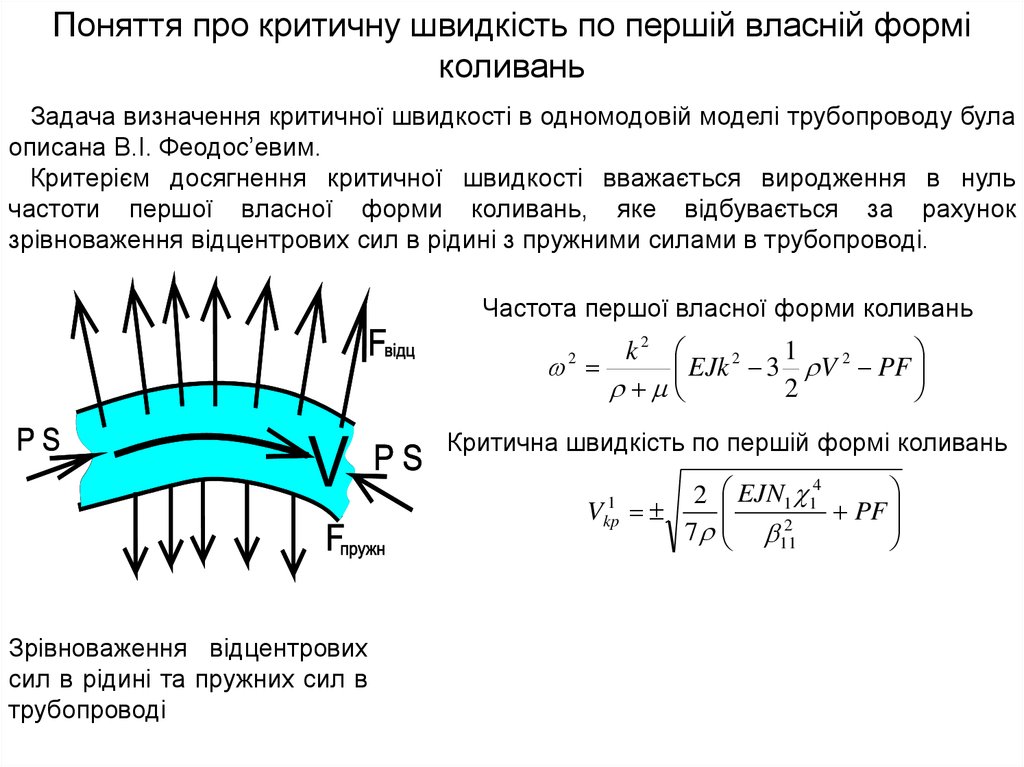
Поняття про критичну швидкість по першій власній форміколивань
Задача визначення критичної швидкості в одномодовій моделі трубопроводу була
описана В.І. Феодос’евим.
Критерієм досягнення критичної швидкості вважається виродження в нуль
частоти першої власної форми коливань, яке відбувається за рахунок
зрівноваження відцентрових сил в рідині з пружними силами в трубопроводі.
Частота першої власної форми коливань
k2
1
2
2
EJk 3 V PF
2
2
Критична швидкість по першій формі коливань
Vkp1
Зрівноваження відцентрових
сил в рідині та пружних сил в
трубопроводі
2 EJN1 14
PF
2
7 11
17.
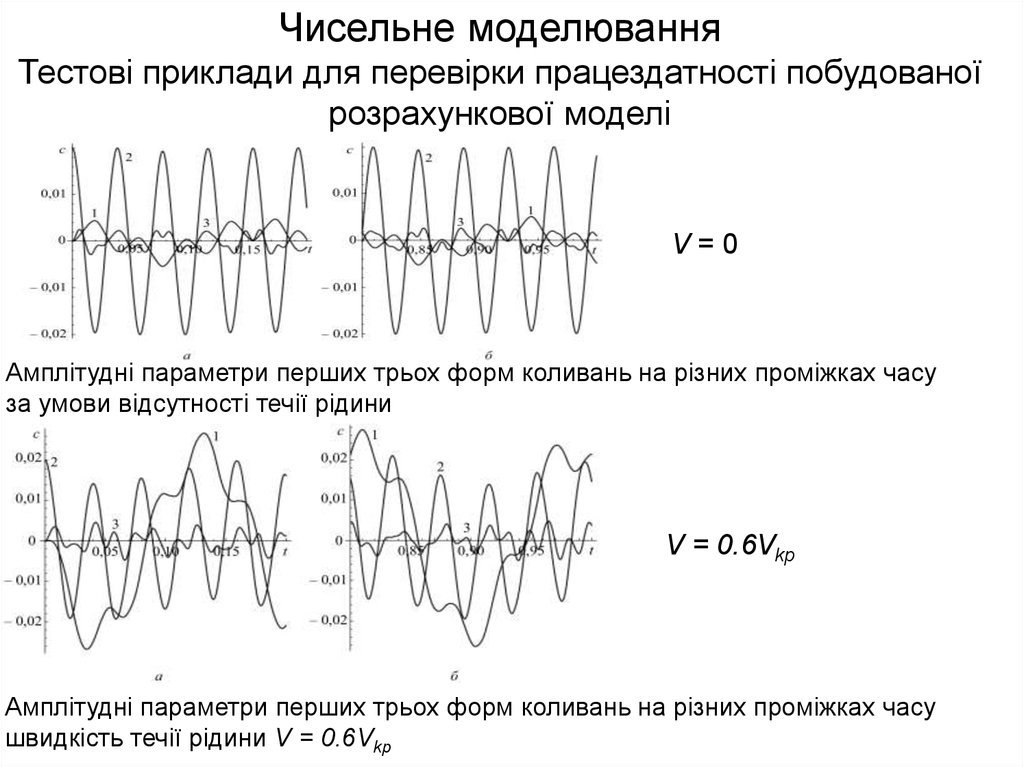
Чисельне моделюванняТестові приклади для перевірки працездатності побудованої
розрахункової моделі
V=0
Амплітудні параметри перших трьох форм коливань на різних проміжках часу
за умови відсутності течії рідини
V = 0.6Vkp
Амплітудні параметри перших трьох форм коливань на різних проміжках часу
швидкість течії рідини V = 0.6Vkp
18.
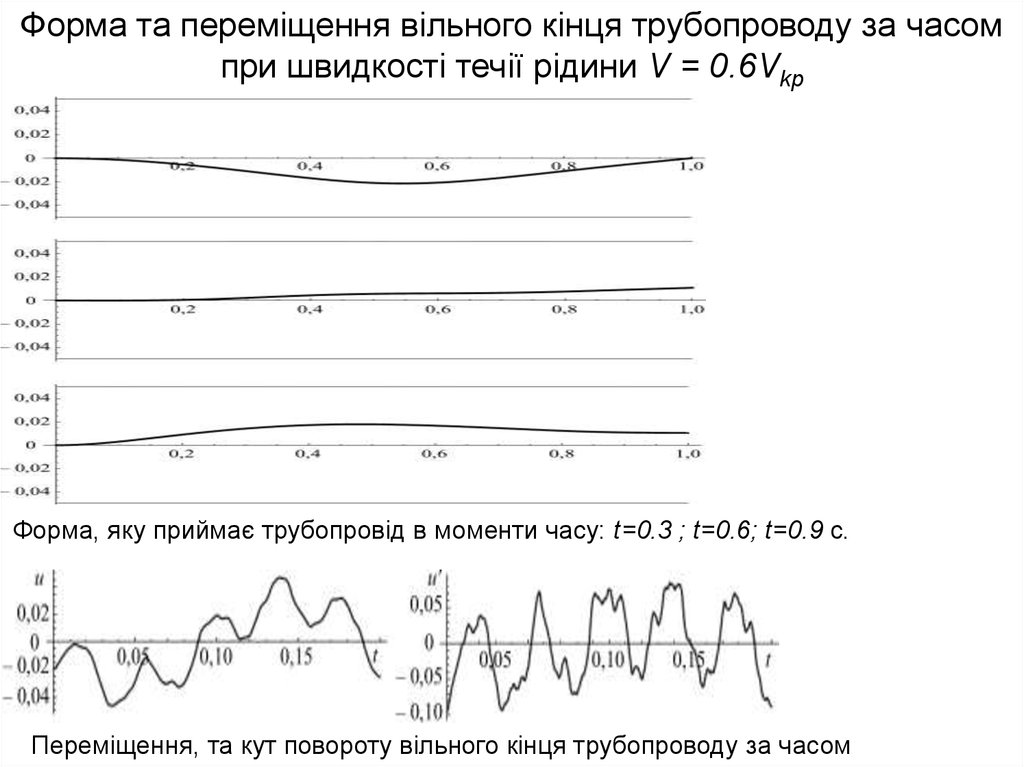
Форма та переміщення вільного кінця трубопроводу за часомпри швидкості течії рідини V = 0.6Vkp
Форма, яку приймає трубопровід в моменти часу: t=0.3 ; t=0.6; t=0.9 c.
Переміщення, та кут повороту вільного кінця трубопроводу за часом
19.
Визначення форми трубопровода в альтернативномуположенні рівноваги
Форма альтернативного положення рівноваги трубопроводу для першої власної
форми u ( x) A1 ( x) C equilibrium (V )
S (k1 l )
Перша власна форма трубопровода як
V (k1 x)
де A1 ( x) U (k1 x)
пружної балки
T (k1 l )
Cequilibrium (V ) Амплітудний коефіцієнт який залежить від швидкості течії рідини
Альтернативна рівновага виникає коли
c1 ' ' (t ) 0
7 V 2
6
c1 (t ) (
21,1 EJ 31,1 PF 21,1 ) c1 (t ) 3 ( EJ d
2
1,1,1,1
1
13
EF d 41,1,1,1 V 2 d 41,1,1,1 ) 0
2
4
Корені c1
в залежності від значення
швидкості
течії
рідини
визначають
амплітудні
коефіцієнти
для
альтернативного
положення
рівноваги
трубопроводу
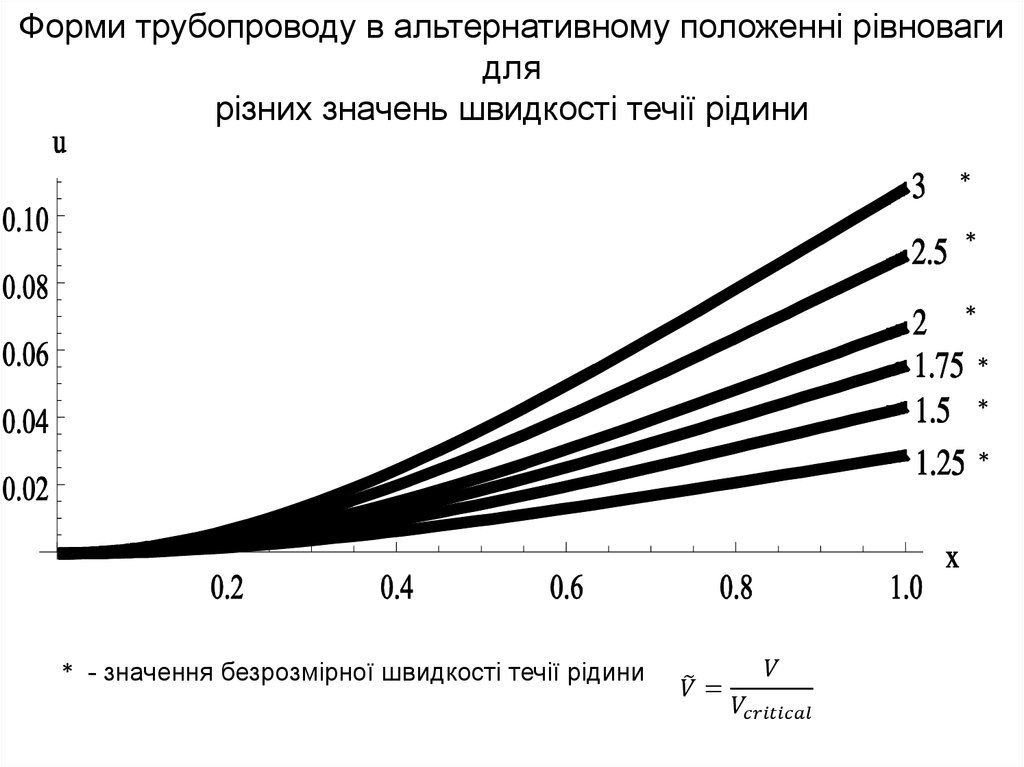
20.
Форми трубопроводу в альтернативному положенні рівновагидля
різних значень швидкості течії рідини
*
*
*
*
*
*
* - значення безрозмірної швидкості течії рідини












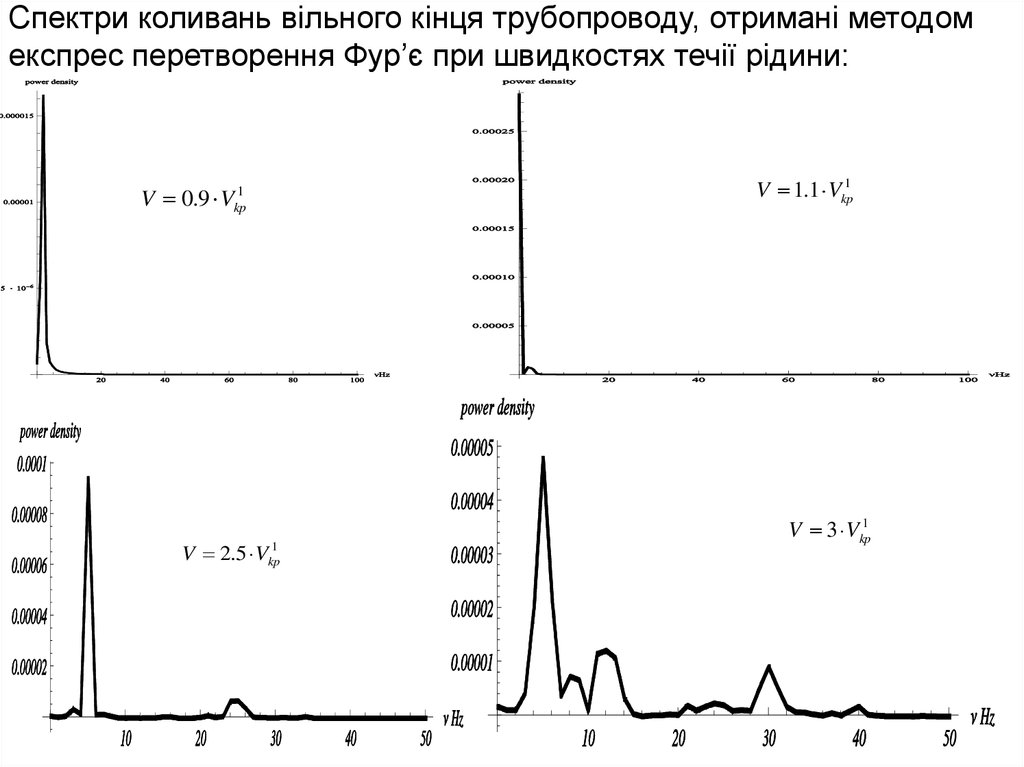
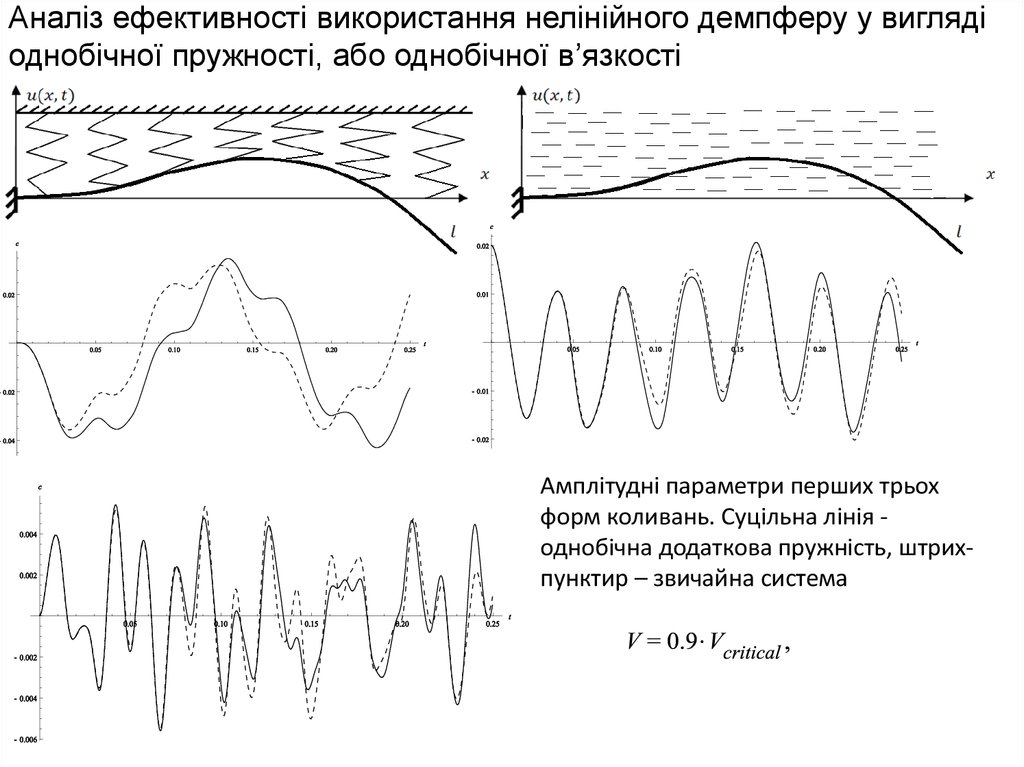
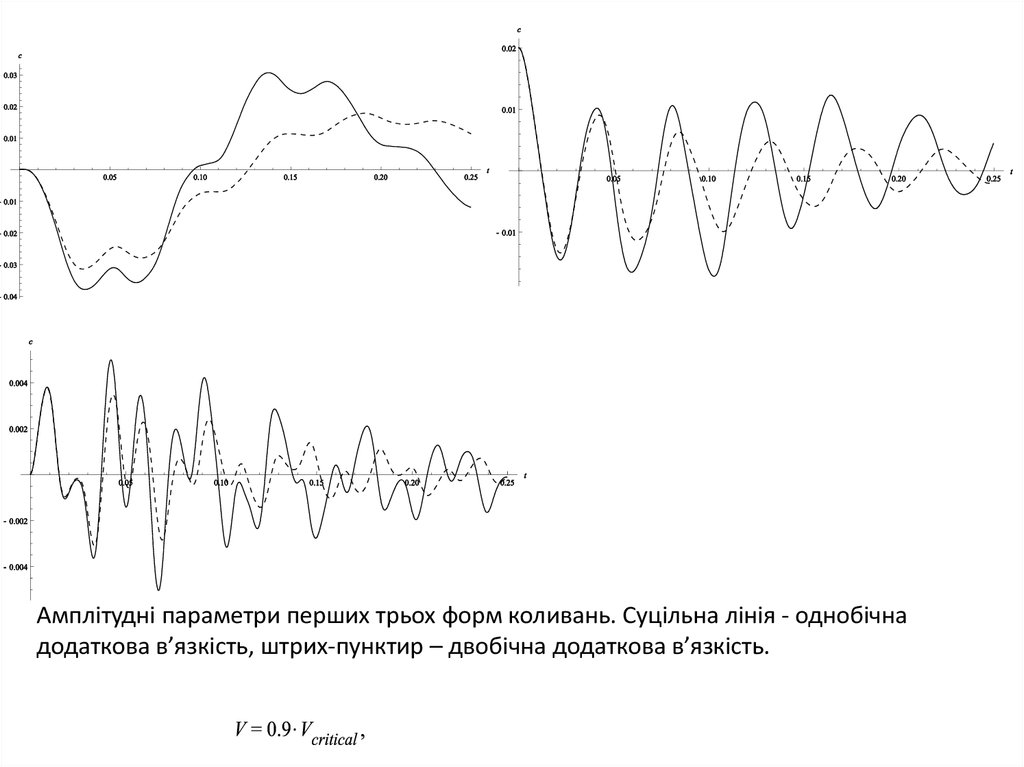
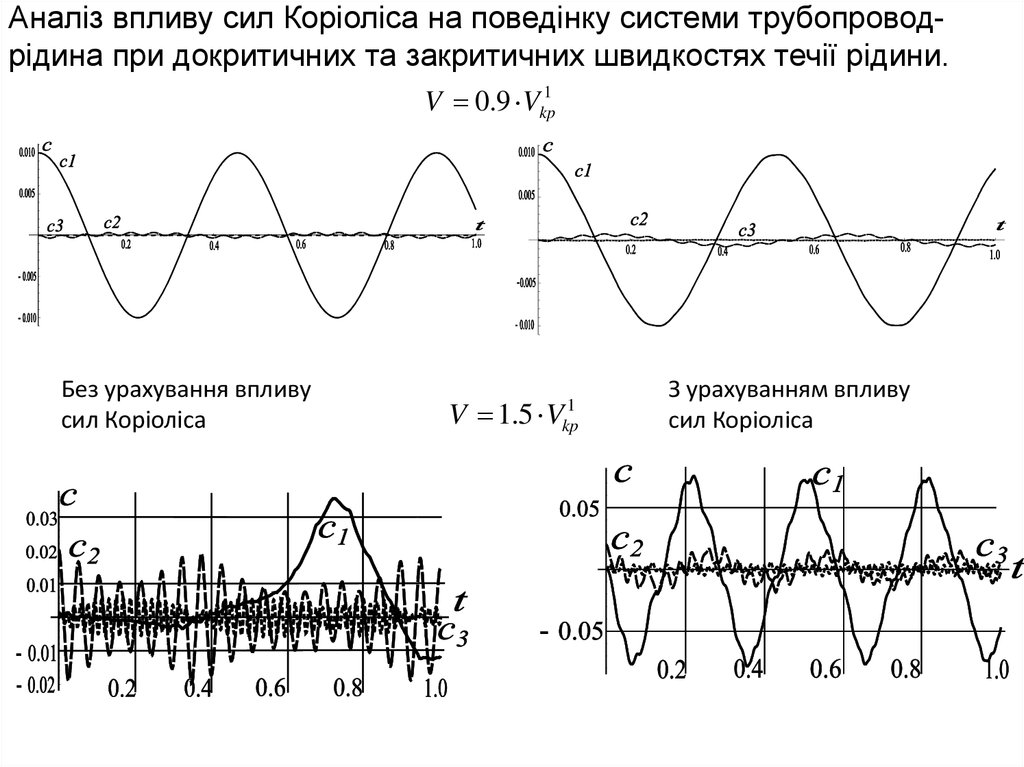


 Физика
Физика








