Электростатическое поле в вакууме. Тема 1

1. Омский государственный технический университет Кафедра физики

Калистратова Л.Ф.
Электронные лекции по разделам
электромагнетизма
(электростатика, постоянный ток, магнетизм)
17 лекций
(34 аудиторных часа)

2. Раздел 1. Электростатика

Перечень изучаемых тем
1. Электростатическое поле в вакууме.
2. Основные теоремы электростатики.
3. Методы расчётов электростатических полей.
4. Электростатическое поле в проводниках.
5. Электростатическое поле в диэлектриках.
6. Энергия электростатического поля.

3. Тема 1. Электростатическое поле в вакууме

План лекции
1. Электрические заряды. Электростатическое поле.
2. Закон Кулона.
3. Напряжённость электростатического поля.
4. Потенциал электростатического поля.
5. Силовые и эквипотенциальные линии.
6. Связь потенциала с напряжённостью/
7. Работа сил электростатического поля.

4. 1. Электрические заряды. Электростатическое поле

В природе существует четыре типа взаимодействия:
гравитационное, электромагнитное, сильное и
слабое.
В основе учения об электричестве и магнетизме лежит
представление об электромагнитном поле.
Электромагнитное поле:
– это особый вид материи, посредством которого
осуществляется электромагнитное
взаимодействие частиц и тел, обладающих
электрическим зарядом.

5.

Электромагнитное поле обладает массой, энергией,
импульсом.
Электромагнитное поле может выступать в виде
отдельных, но неразрывно связанных сторон –
электрического и магнитного поля.
Электрическое поле:
- создается электрическими зарядами;
- изменяющимся магнитным полем;
- передает действие электрических сил.
Магнитное поле:
- создается движущимися электрическими зарядами;
- изменяющимся электрическим полем;
- передает действие магнитных сил.

6.

Электрические и магнитные явления неразрывны,
хотя во многих случаях их можно рассматривать
раздельно.
М. Фарадею пришлось проделать не менее 100
опытов, чтобы открыть явление электромагнитной
индукции, отражающее взаимосвязь
электрических и магнитных явлений.
Теория электромагнетизма укладывается в рамки
уравнений Максвелла, великая заслуга которого
состоит в теоретическом осмыслении электрических
и магнитных явлений.

7.

Уравнения Максвелла описывают свойства и
распространение электромагнитного поля в любой
среде.
Так в вакууме электромагнитное поле
(электромагнитные волны) распространяется со
скоростью света, равной 3 .10 8 м/с.
Отсюда Максвелл проследил связь электрических и
магнитных явлений с оптикой и пришёл к пониманию
электромагнитной природы света и излучений.

8.

Движение электрических зарядов создает
электрический ток.
Получение и использование электрической энергии
изменило весь образ жизни человечества.
Большой вклад в понимание законов электрического
тока внесли ученые Ампер, Ом, Джоуль, Ленц,
Кирхгоф.
Электрические цепи любой сложности можно
рассчитать, основываясь на законах Ома и
правилах Кирхгофа.

9.

Электрическое поле
бывает:
- электростатическое:
- непостоянное;
- переменное.
Электростатическое поле:
- существует вокруг неподвижных зарядов и не
отделимо от них;
- обладает энергией, импульсом, массой;
- обусловливает взаимодействие неподвижных
зарядов.

10.

Электрический заряд (q):
- мера интенсивности электромагнитного
взаимодействия;
- внутренняя характеристика элементарной
частицы;
- скалярная величина, измеряемая в кулонах:
[q] = 1Кл.
Принято условно считать заряд наэлектризованной
стеклянной палочки:
- положительным;
заряд наэлектризованной янтарной палочки
- отрицательным.

11.

Элементарными названы самые маленькие заряды
природы:
- отрицательный заряд имеет электрон,
- положительный заряд имеет позитрон (античастица
электрона) и протон.
Величина заряда электрона и протона:
е = 1,6 10 –19 Кл
Точечным называется заряд, сосредоточенный на
теле, размерами которого можно пренебречь.
Пробным называется малый по модулю точечный
заряд, не искажающий величину и конфигурацию
исследуемого
электростатического
поля
в
пространстве.

12.

Одним из способов получения зарядов является
трение.
Появляющиеся при трении заряды являются суммой
элементарных зарядов:
+ q = е+
- q = е–
Закон сохранения электрического заряда:
алгебраическая сумма зарядов электрически
изолированной системы остается неизменной.
q = const

13.

Для измерения величины заряда служит
электрометр

14. 2. Закон Кулона

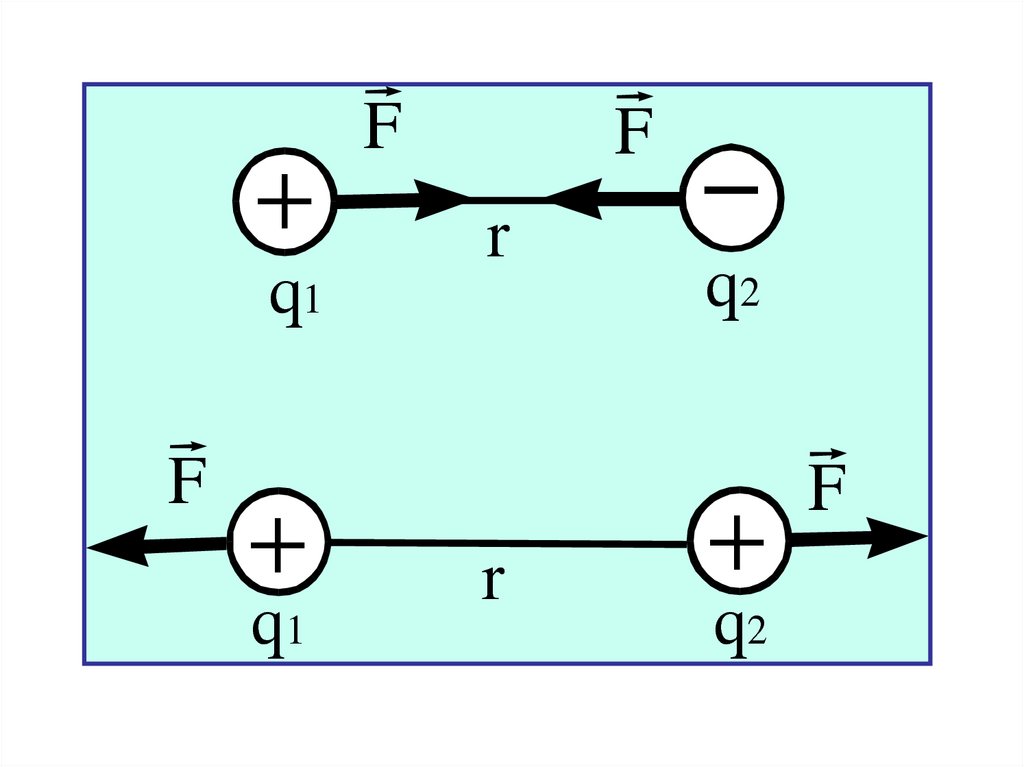
Взаимодействие точечных зарядов происходит по
линии, соединяющей заряды.
Электрические силы, характеризующие
взаимодействие зарядов, называются
электростатическими или кулоновскими.
Одноименные заряды отталкиваются друг от друга,
разноименные заряды - притягиваются.

15.

+
q1
F
+
q1
F
F
r
r
_
q2
+
q2
F

16.

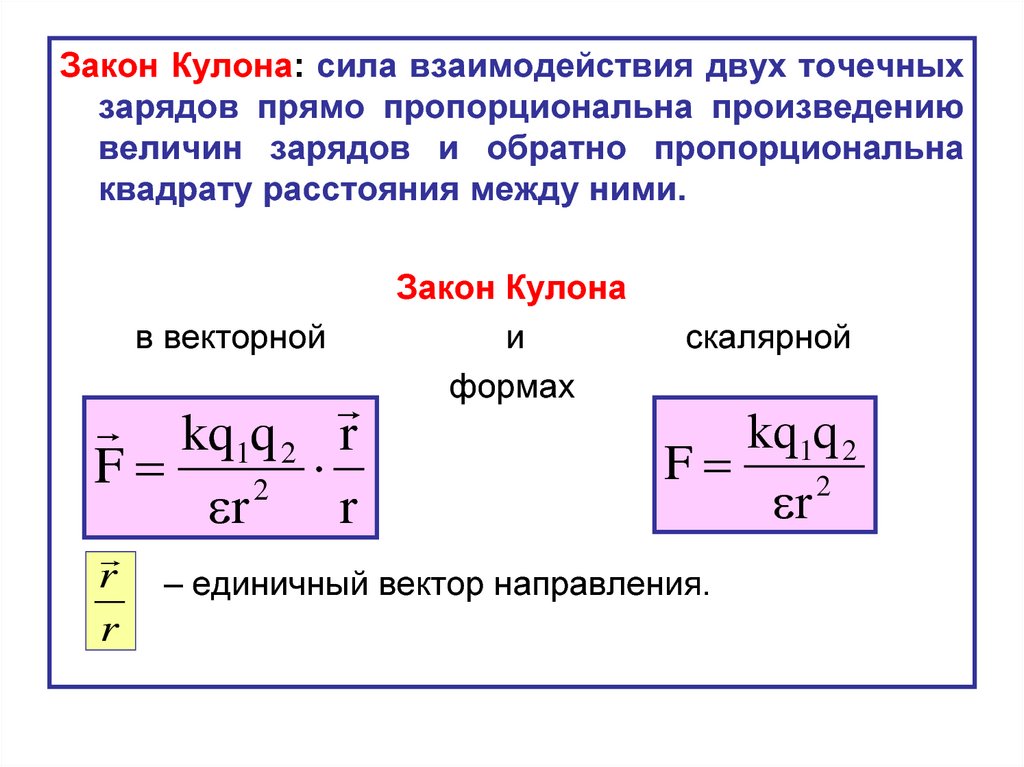
Закон Кулона: сила взаимодействия двух точечных
зарядов прямо пропорциональна произведению
величин зарядов и обратно пропорциональна
квадрату расстояния между ними.
в векторной
kq1q 2
F
2
r
r
r
r
r
Закон Кулона
и
формах
скалярной
kq1q 2
F
2
r
– единичный вектор направления.

17.

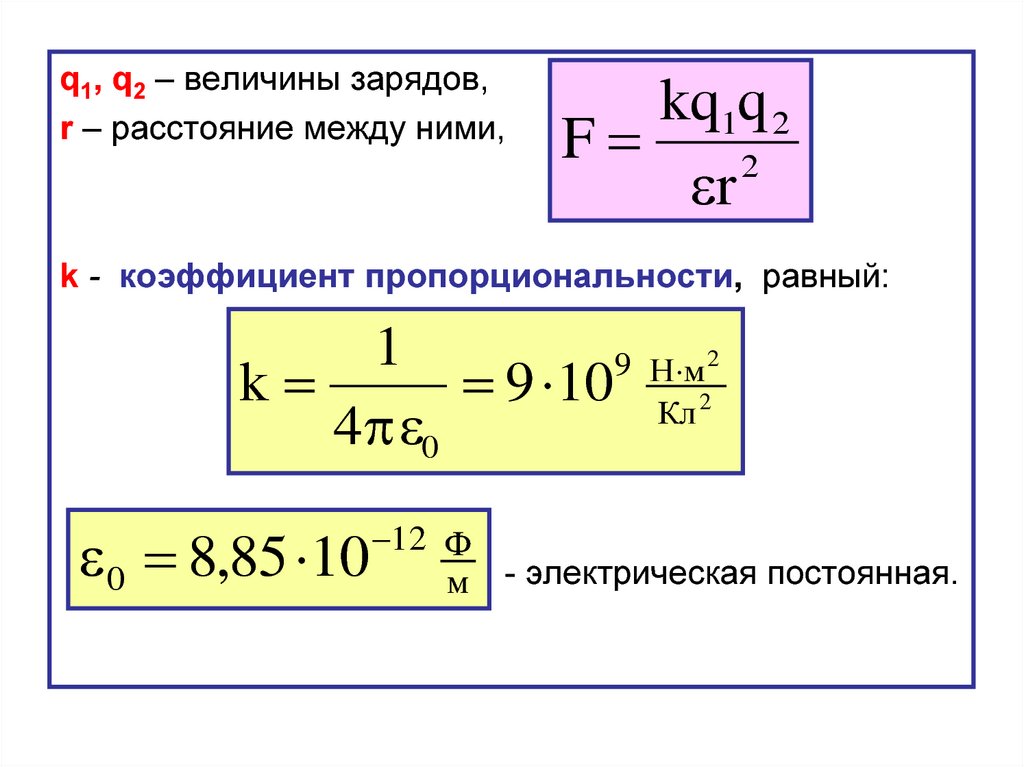
q1, q2 – величины зарядов,
r – расстояние между ними,
kq1q 2
F
2
r
k - коэффициент пропорциональности, равный:
1
9
k
9 10
4 0
0 8,85 10
Н м 2
Кл 2
12 Ф
м - электрическая постоянная.

18.

Наиболее сильно заряды взаимодействуют в вакууме.
– диэлектрическая проницаемость среды.
Диэлектрическая проницаемость показывает, во
сколько раз сила взаимодействия точечных
зарядов в среде меньше, чем в вакууме.
FВАК
FСР
Для воды = 81, для стекла = 2, для фарфора = 6,
для вакуума и воздуха = 1.

19.

Сила Кулона
прямо пропорциональна
величине заряда
F
Сила Кулона
обратно
пропорциональна
квадрату расстояния
F
q
r

20.

Принцип суперпозиции
для электрических сил

21.

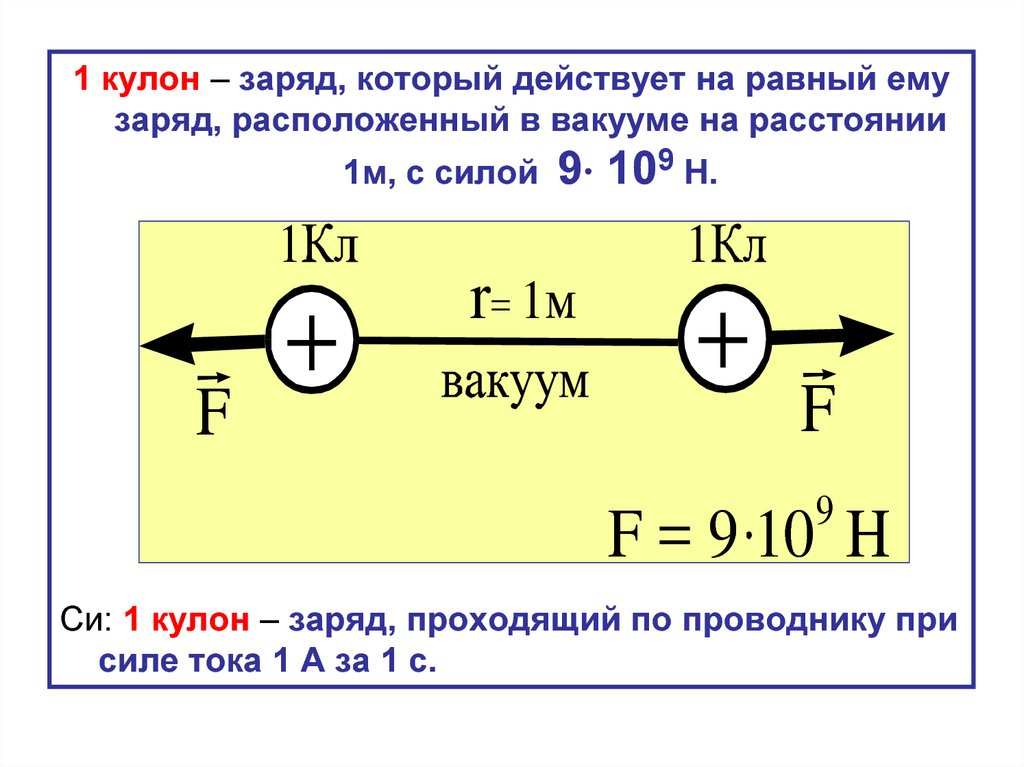
1 кулон – заряд, который действует на равный ему
заряд, расположенный в вакууме на расстоянии
1м, с силой
1
F
+
r= 1
9 109 Н.
1
+
F
9
F = 9 10 H
Си: 1 кулон – заряд, проходящий по проводнику при
силе тока 1 А за 1 с.

22.

Для тел правильной геометрической формы при
равномерном распределении заряда (стержень,
плоскость, шар), заряд можно представить как
алгебраическую сумму точечных зарядов dq:
q dq
dq = dl (стержень),
dq = dS (плоскость),
dq = dV (шар).
dl, dS, dV – элементы длины, площади поверхности и
объёма соответственно.

23.

– линейная плотность заряда - заряд,
приходящийся на единицу длины стержня:
dq
dl
Кл м
– поверхностная плотность заряда - заряд,
приходящийся на единицу площади поверхности:
dq
dS
Кл м
– объёмная плотность заряда -
2
заряд,
приходящийся на единицу объёма:
dq
dV
Кл м
3

24. 3. Напряженность электростатического поля.

-
Электростатическое поле:
среда, передающая взаимодействие неподвижных
электрических зарядов;
существует вокруг неподвижного заряда;
существует в природе независимо от нас;
не воспринимается органами чувств человека;
материально (обладает энергией и массой).
Основные характеристики электростатического поля –
напряжённость и потенциал не зависят от
времени.

25.

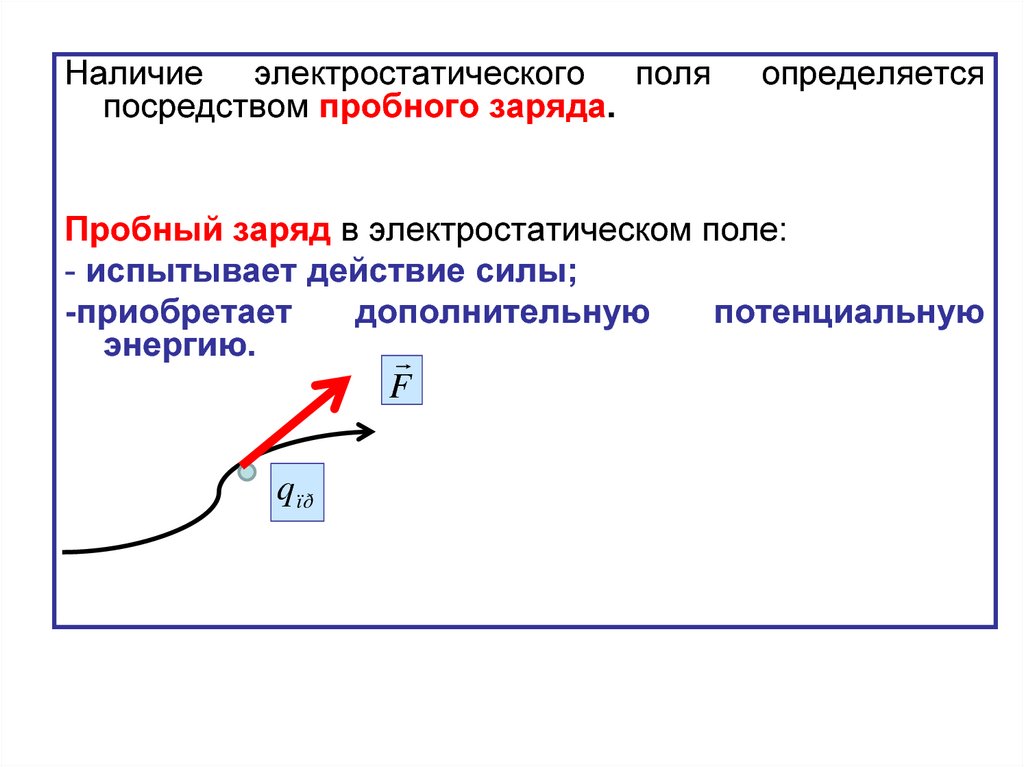
Наличие электростатического поля
посредством пробного заряда.
определяется
Пробный заряд в электростатическом поле:
- испытывает действие силы;
-приобретает
дополнительную
потенциальную
энергию.
F
q ïð

26.

Если в одну и ту же точку поля вносить разные по
величине пробные заряды qпр1, qпр2, , то со
стороны поля на них будут действовать разные
силы F1 , F2 .
Отношения сил к величине пробных зарядов равны
между собой:
F1
F2
F
const E
q пр1 q пр 2
q пр
Величина
F
E
q пр
F
E
q пр
называется напряженностью электрического поля.

27.

Напряженность электрического поля:
- равна силе, действующей со стороны поля на
положительный единичный пробный заряд,
помещенный в данную точку поля;
- векторная величина;
- силовая характеристика поля;
F
E
q пр
- характеристика только одной точки поля;
- измеряется в вольтах на метр:
Â
E
ì

28.

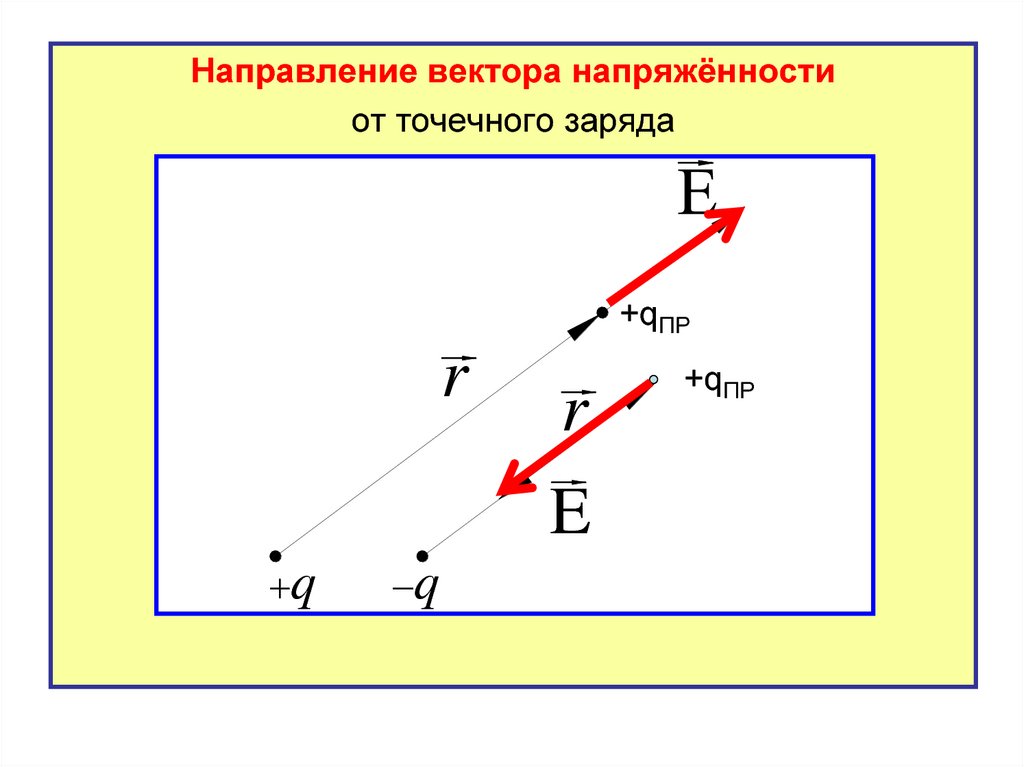
Направление вектора напряжённости
от точечного заряда
+qПР
r
r
E
q
q
+qПР

29.

Принцип суперпозиции: напряженность поля,
созданного системой точечных зарядов равна
векторной сумме напряженностей полей,
создаваемых каждым зарядом в отдельности.
E E1 E 2 E3 ... E n
При непрерывном распределении зарядов
суммирование заменяется интегрированием
элементарных напряженностей dE , создаваемых
отдельными элементарными порциями заряда dq.
n
E Ei
i 1
E dE

30.

Принцип суперпозиции
на примере двух точечных зарядов
q1
E1
E2
E E1 E 2
E
q2
E E E 2E1E 2 cos
2
1
2
2

31.

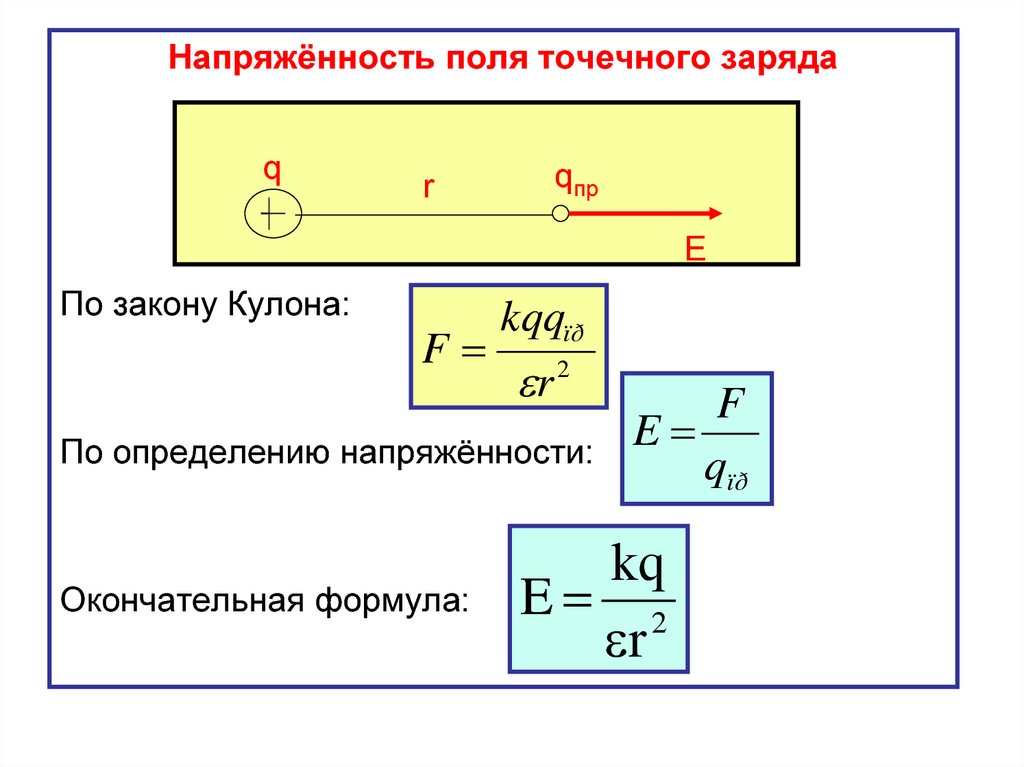
Напряжённость поля точечного заряда
q
r
qпр
Е
По закону Кулона:
F
kqqïð
r 2
По определению напряжённости:
Окончательная формула:
F
E
qïð
kq
E 2
r

32.

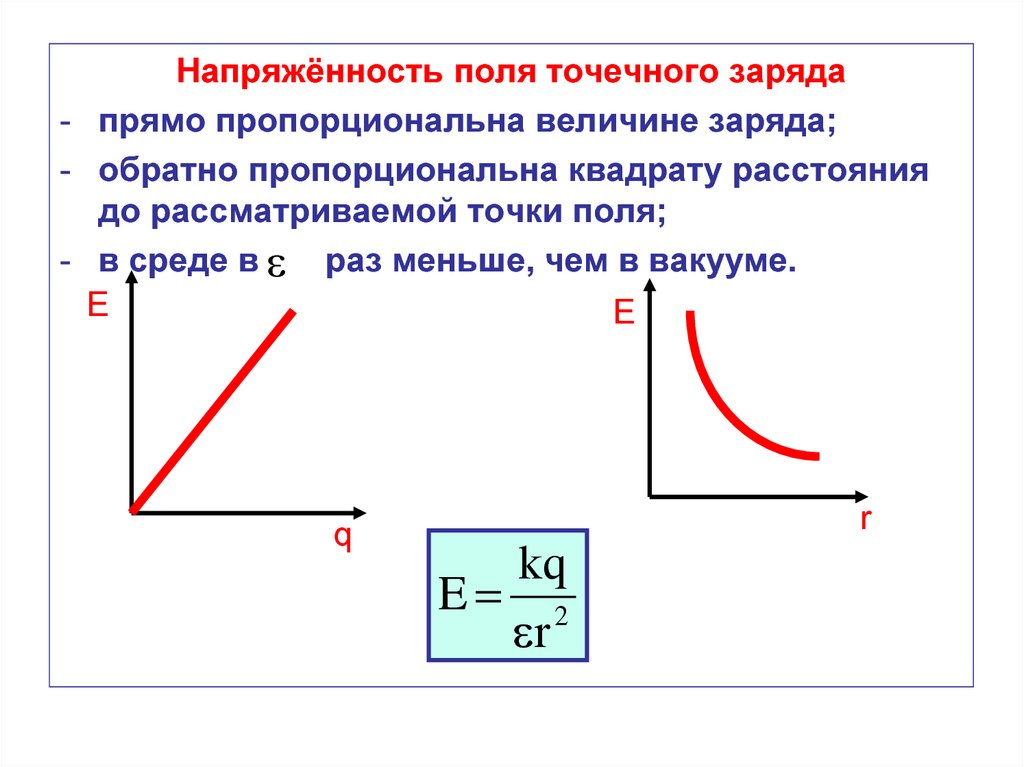
Напряжённость поля точечного заряда
- прямо пропорциональна величине заряда;
- обратно пропорциональна квадрату расстояния
до рассматриваемой точки поля;
- в среде в раз меньше, чем в вакууме.
Е
E
q
r
kq
E 2
r

33. 4. Потенциал электростатического поля

В одной и той же точке электрического поля пробные
заряды разной величины qпр1, qпр2, , qпр n
приобретают соответствующую различную
потенциальную энергию Wп1, Wп2, , Wпn.
Отношения потенциальной энергии к величине пробного
заряда равны:
Wп1 Wп 2
Wп
const
q пр1 q пр 2
q пр

34.

Величина
называется потенциалом.
Wп
q пр
Потенциал электростатического поля:
- равен потенциальной энергии, которой обладает
единичный положительный пробный заряд,
помещенный в данную точку поля;
- является энергетической характеристикой поля;
- характеристика только одной точки поля;
- скалярная величина;
- измеряется в вольтах: [ ] = B.

35.

Как и потенциальная энергия, потенциал точки
электрического поля измеряется с точностью до
произвольной постоянной.
Чтобы избежать неточностей в определении
потенциала, рассматривают не одну, а две точки
электрического поля.
Тогда
Wп1 Wп 2
1 2
q пр
Поскольку убыль потенциальной энергии равна работе
сил электрического поля ( Wп1 Wп2 A12 ), то разность
потенциалов можно записать как
A12 A
1 2
12
1 2 q пр
q пр

36.

Разность потенциалов двух точек поля равна работе
сил электрического поля по перемещению
положительного единичного пробного заряда
между этими точками.
A12
qïð
Потенциал положительного заряда принято считать
положительной величиной ( 0).
Потенциал отрицательного заряда – отрицательной
величиной ( < 0).

37.

Принцип суперпозиции для потенциала:
потенциал в точке поля, созданного системой
точечных зарядов, равен скалярной сумме
потенциалов полей отдельных зарядов.
1 2
Если заряд нельзя считать точечным, то его можно
разбить на отдельные точечные заряды dq,
создающие потенциалы d i .
Тогда принцип суперпозиции можно записать в виде
d

38.

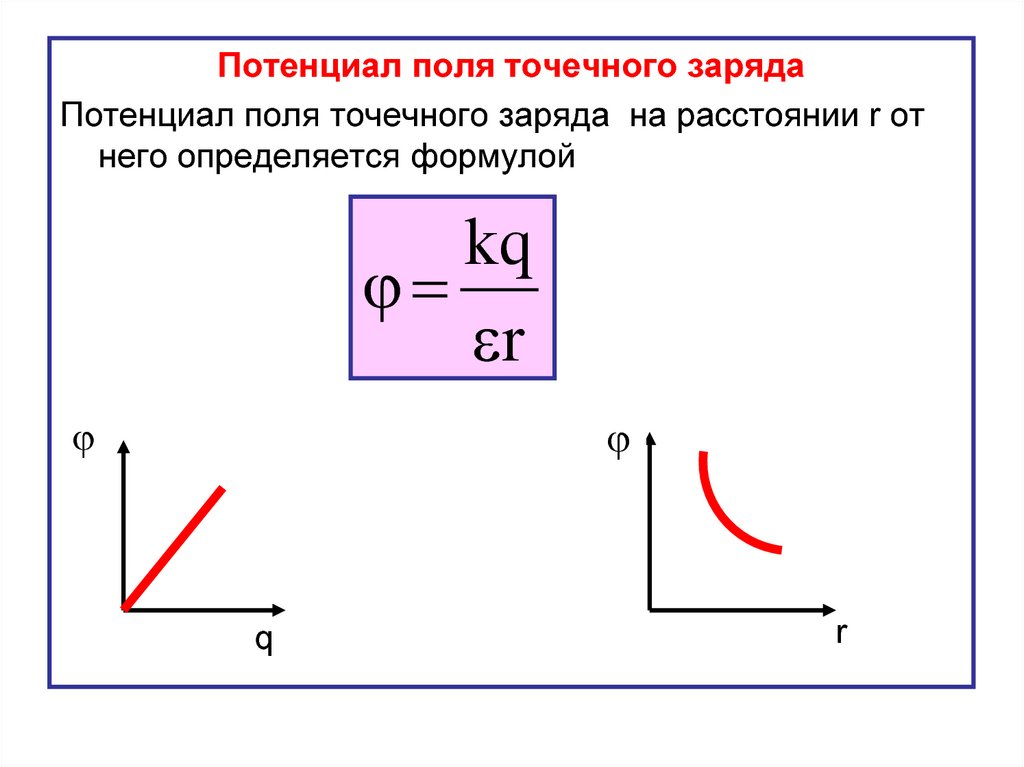
Потенциал поля точечного заряда
Потенциал поля точечного заряда на расстоянии r от
него определяется формулой
kq
r
q
r

39. 5. Силовые и эквипотенциальные линии

Силовой линией (или линией напряжённости)
называется линия, в каждой точке которой вектор
напряженности направлен по касательной.
Силовые линии:
- начинаются на положительных зарядах (или в
бесконечности) и заканчиваются на
отрицательных зарядах (или в бесконечности);
- не пересекаются;
- густота силовых линий (число линий,
пересекающих единичную площадку) равна
значению напряженности в заданном месте поля.

40.

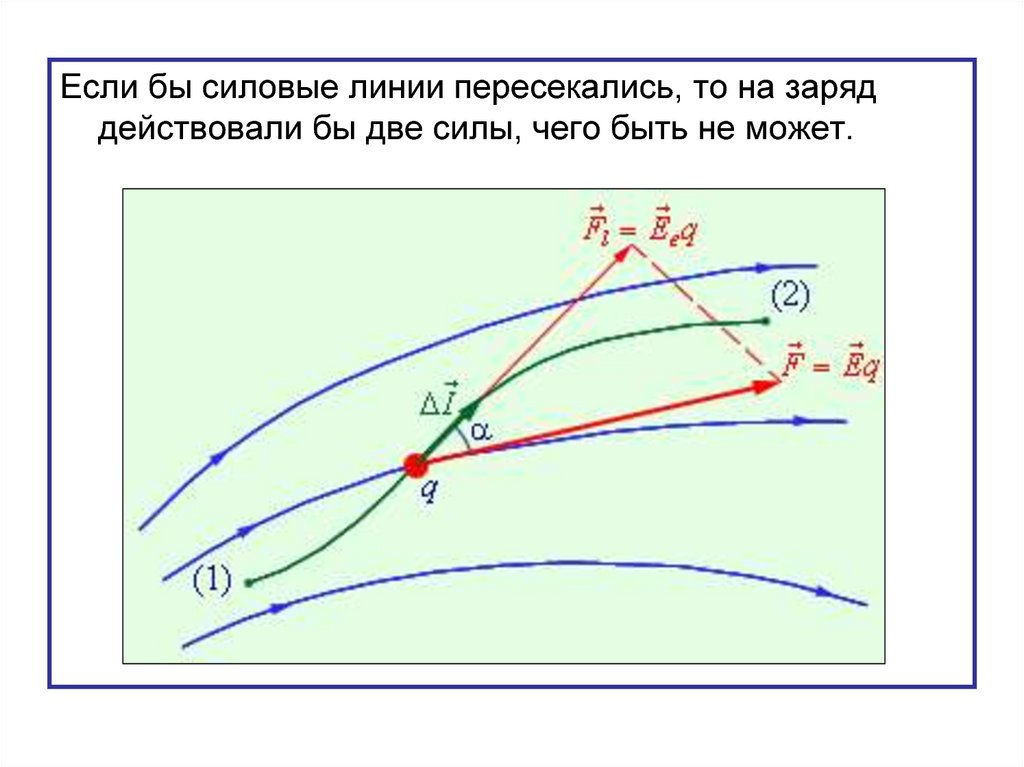
41.

Если бы силовые линии пересекались, то на заряд
действовали бы две силы, чего быть не может.

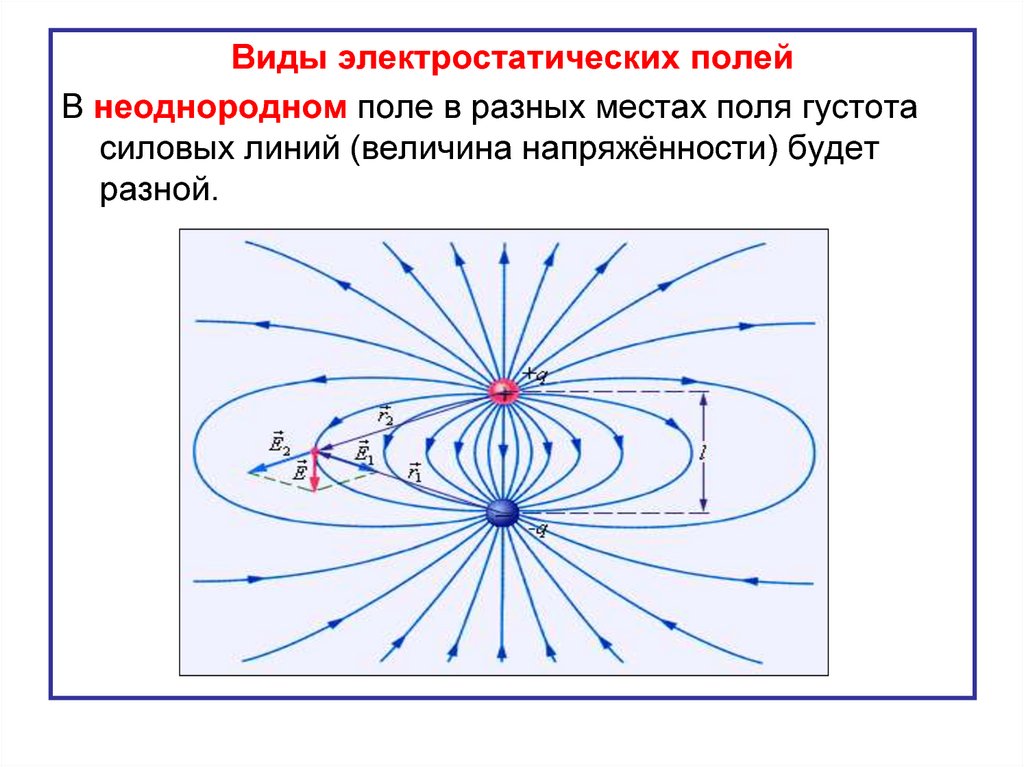
42.

Виды электростатических полей
В неоднородном поле в разных местах поля густота
силовых линий (величина напряжённости) будет
разной.

43.

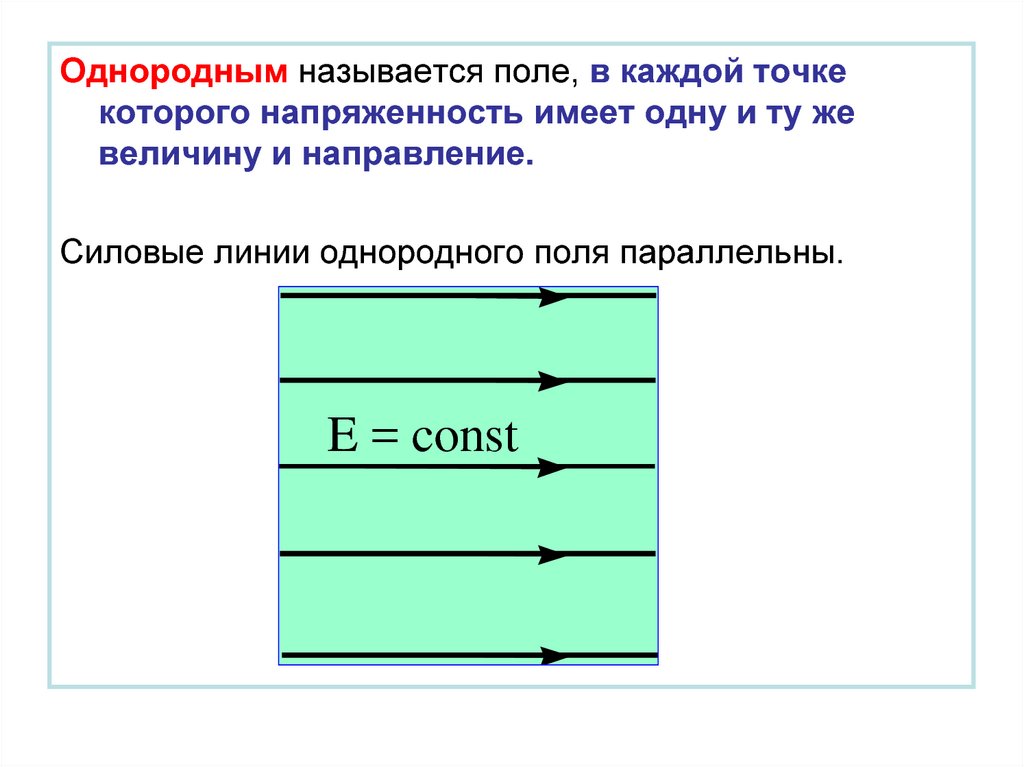
Однородным называется поле, в каждой точке
которого напряженность имеет одну и ту же
величину и направление.
Силовые линии однородного поля параллельны.
E = const

44.

В центральном поле силовые линии (или их
продолжения) сходятся в одной точке.

45.

Эквипотенциальная линия (или поверхность) геометрическое место точек равного
потенциала.
Эквипотенциальные линии обладают следующими
свойствами:
1) работа сил электрического поля вдоль
эквипотенциальной линии равна нулю;
2) перпендикулярны силовым линиям в каждой
точке поля;
3) напряжённость поля направлена в сторону
убывания потенциала.

46.

Докажем пункт «2».
E
q
dr
const

47.

Действительно, если заряд q перемещать вдоль
эквипотенциальной линии, то 1 = 2.
A q 1 2 0
Тогда
С другой стороны работу определим как
A Fdr qEdr q пр E dr cos
Нулю может быть равен только cos .
Следовательно, угол
между направлением вектора
напряженности E и вектором элементарного
перемещения dr равен 90О: 2

48.

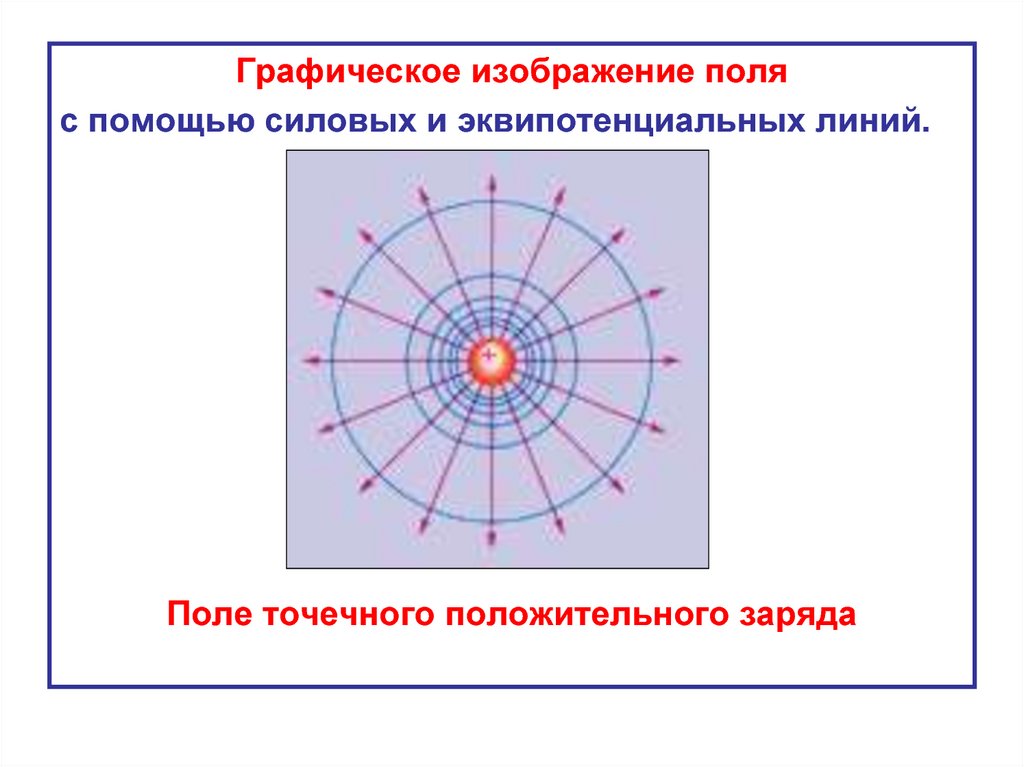
Графическое изображение поля
с помощью силовых и эквипотенциальных линий.
Поле точечного положительного заряда

49.

Электростатическое поле диполя

50.

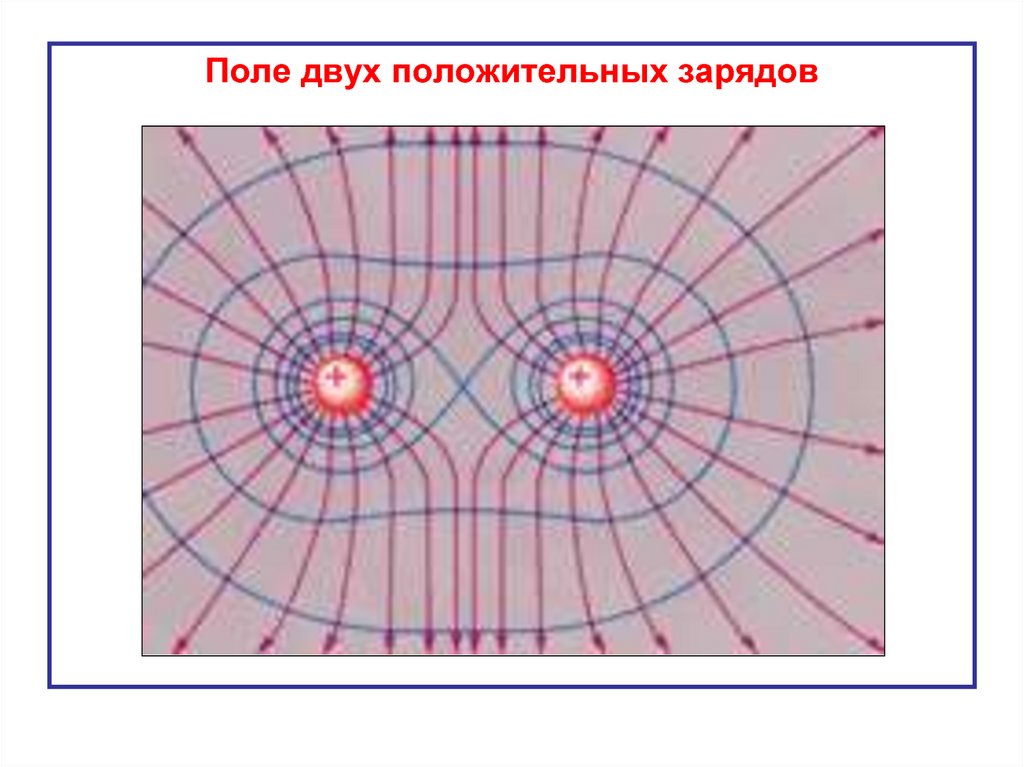
Поле двух положительных зарядов

51. 6. Связь потенциала с напряжённостью

Напряженность и потенциал являются
характеристиками одной и той же точки поля, значит
они связаны между собой.
Пусть в однородном электрическом поле заряд q
перемещается из точки
E = const
с потенциалом 1, в точку
с потенциалом 2, отстоящие
2
на расстоянии dr друг от друга.
1

52.

Элементарную работу сил поля можно определить как
dA Fdr qEdr
qEdr cos qEr dr
Er – проекция вектора напряженности на направление
перемещения.
C другой стороны эту же элементарную работу можно
записать как
dA q( 1 2 ) qd

53.

Объединяя обе формулы, получим
d
Er
dr
Из этого выражения следует, что напряжённость:
- равна изменению потенциала на единичном
расстоянии;
- направлена в сторону убывания потенциала (на
это указывает знак минус).

54.

d d d
E
i
j
k
dy
dz
dx
E grad
Напряженность в каждой точке поля равна
градиенту потенциала в этой же точке, взятому с
обратным знаком.

55.

Для точечного заряда:
z
E
grad
+
q
y
1
2 1
x

56.

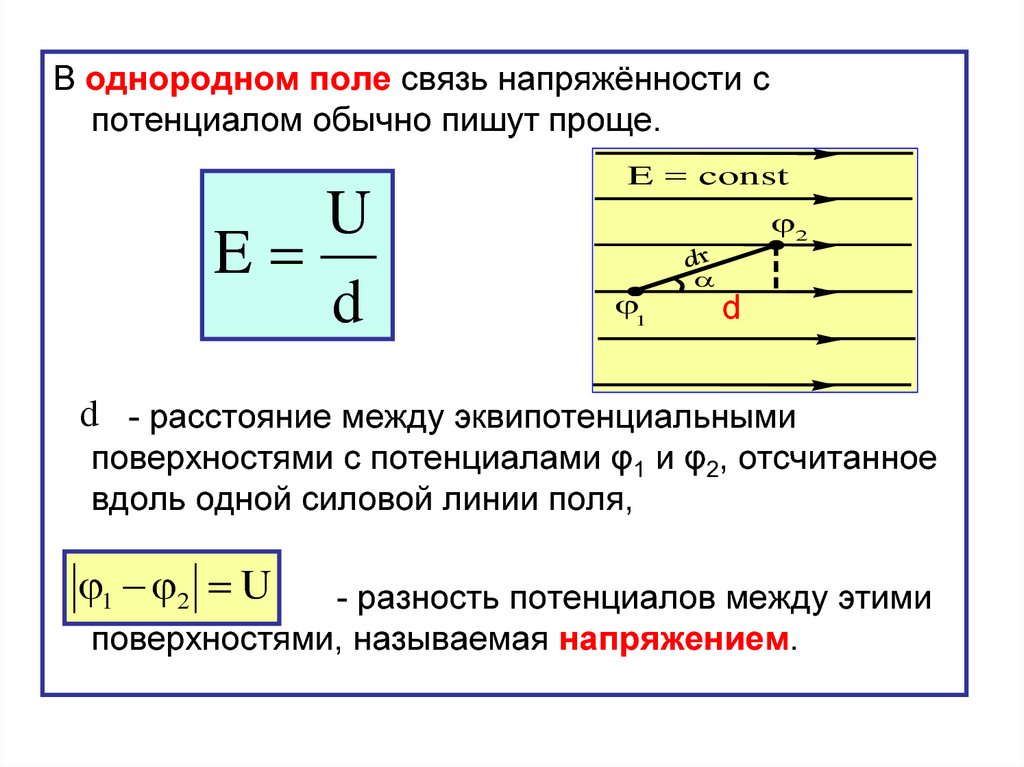
В однородном поле связь напряжённости с
потенциалом обычно пишут проще.
U
E
d
E = const
2
1
d
d - расстояние между эквипотенциальными
поверхностями с потенциалами φ1 и φ2, отсчитанное
вдоль одной силовой линии поля,
1 2 U
- разность потенциалов между этими
поверхностями, называемая напряжением.

57.

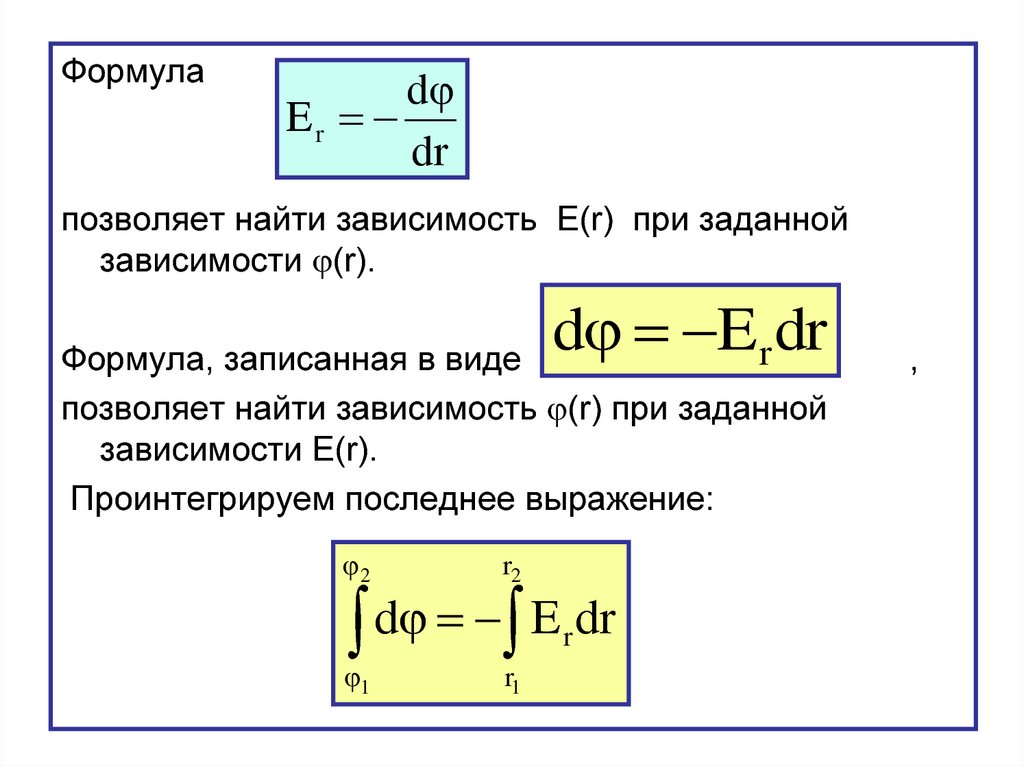
Формула
d
Er
dr
позволяет найти зависимость E(r) при заданной
зависимости (r).
d Er dr
Формула, записанная в виде
позволяет найти зависимость (r) при заданной
зависимости Е(r).
Проинтегрируем последнее выражение:
2
r2
d E dr
r
1
r1
,

58.

После интегрирования получим:
r2
2 1 E r dr
r1
В более общем виде формула для расчёта потенциала
выглядит как
r2
r 0 E r r dr
r1
Окончательная формула позволяет найти зависимость
(r), если известна формула зависимости E r .

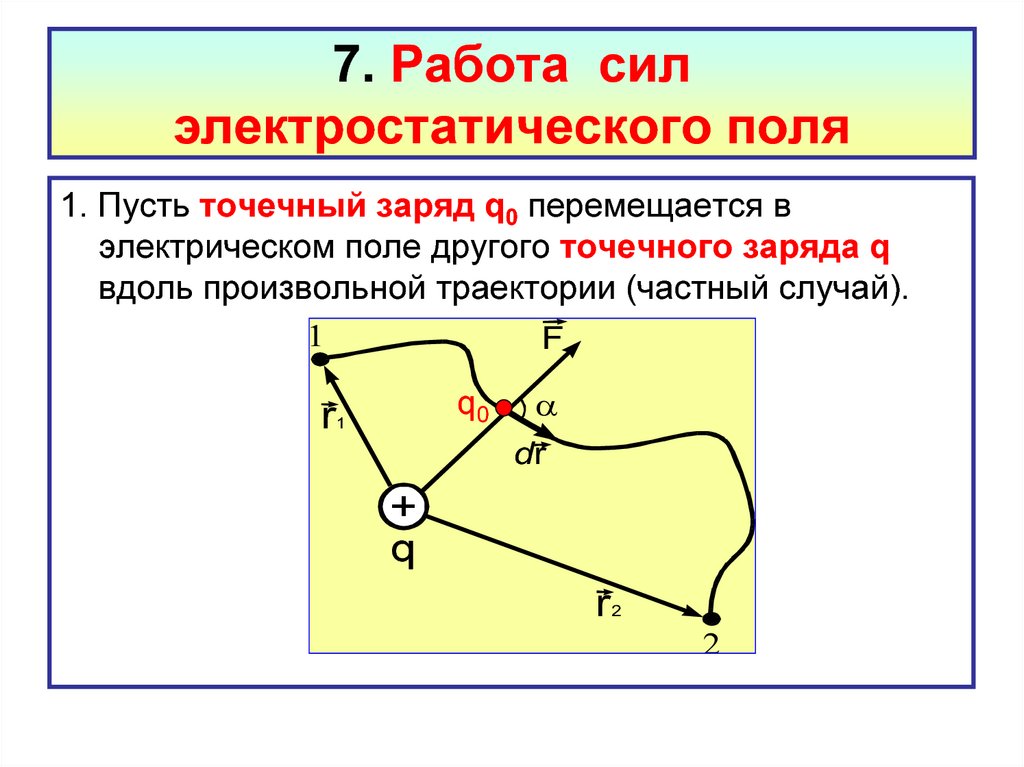
59. 7. Работа сил электростатического поля

1. Пусть точечный заряд q0 перемещается в
электрическом поле другого точечного заряда q
вдоль произвольной траектории (частный случай).
F
q0
r
1
dr
+
q
r
2

60.

Начальная точка перемещения
(точка 1) задается
радиус-вектором r1 , а конечная
точка перемещения
(точка 2) радиус-вектором r2 .
Между двумя зарядами q и q0 в любой точке
траектории действует кулоновская сила F.
qq 0
F k 2
r
Элементарная работа этой силы на элементарном
перемещении равна
dA Fd r Fr dr

61.

Полная работа при перемещении заряда q0 из точки 1
в точку 2 определится суммированием элементарных
работ:
1 1
kqq 0
A12 dA Fr dr 2 dr kqq 0
r
r1 r2
1
r1
r1
2
r2
Выделим формулу
r2
1 1
A12 kqq 0
r1 r2
Она определяет работу по переносу точечного
заряда qO в поле точечного заряда q (частный
случай).

62.

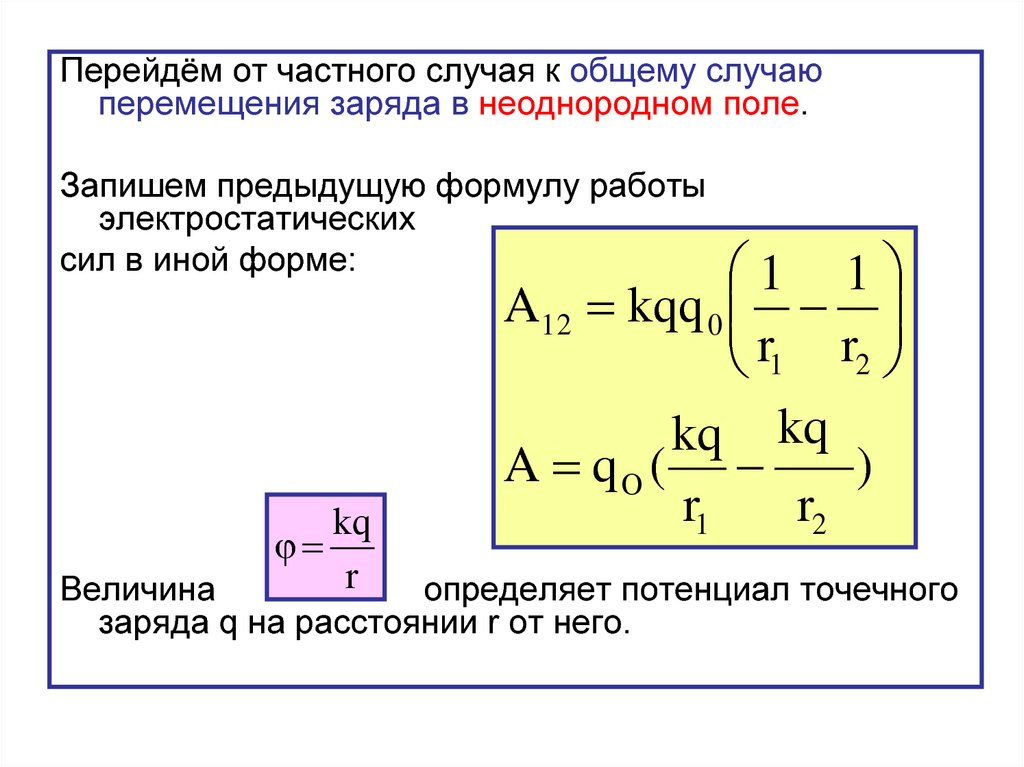
Перейдём от частного случая к общему случаю
перемещения заряда в неоднородном поле.
Запишем предыдущую формулу работы
электростатических
сил в иной форме:
kq
r
1 1
A12 kqq 0
r1 r2
kq kq
A qO (
)
r1
r2
Величина
определяет потенциал точечного
заряда q на расстоянии r от него.

63.

A12 q O 1 2
Работа по перемещению заряда в любом
неоднородном поле равна произведению
величины этого заряда на разность потенциалов
начальной и конечной точек пути.
A12 qO

64.

qo
1
A12 q O 1 2
2

65.

В однородном электростатическом поле разность
потенциалов и напряжённость связаны формулой:
U Ed
Работа электрических сил в этом случае запишется как
A12 q O U
A12 q O Ed

66.

2
qO
E = const
d
2
1
A12 q O Ed

67.

Работа сил электростатического поля:
- определяется только положением начальной и
конечной точек перемещения;
- не зависит от формы траектории;
- равна нулю по замкнутой траектории.
dA A 0
L
На основании этого можно утверждать, что:
- электростатические силы консервативны,
- электростатическое поле – потенциально.