Непрерывность функции

1. Непрерывность функции

Дифференциальное
Для
добавления текста
исчисление
щелкните
мышью

2. Определение непрерывности функции

lim
f(x) f(x0)
x
x0
lim
f(x) 0
x
0

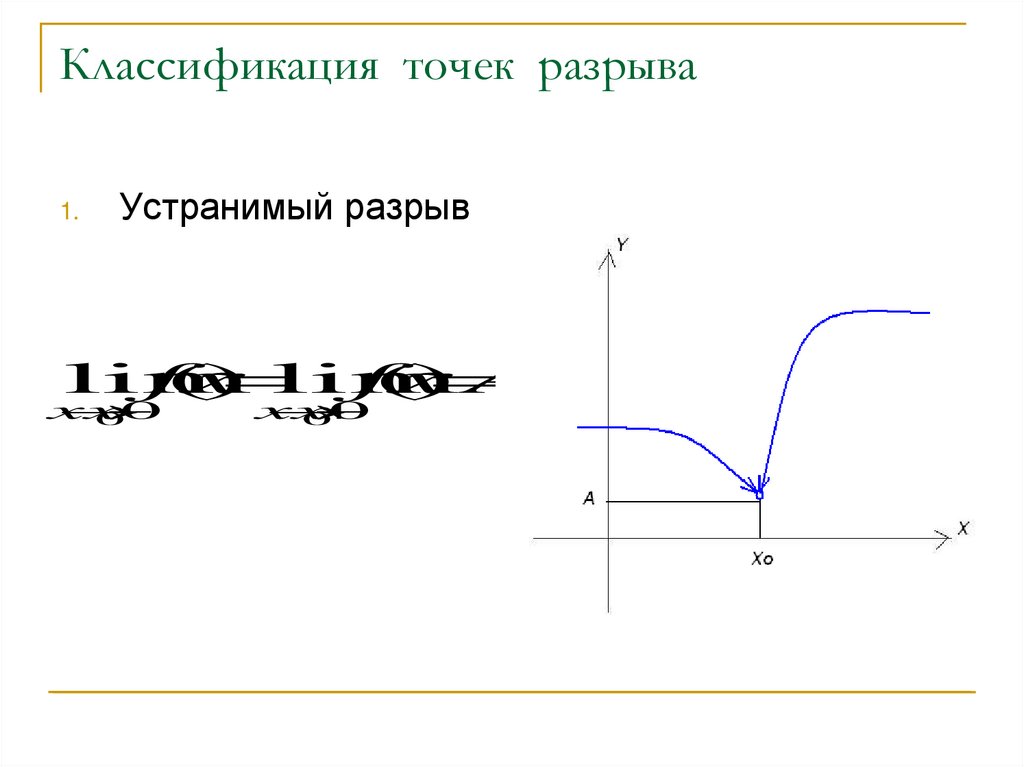
3. Классификация точек разрыва

1.
Устранимый разрыв
lim
f(
x
)
lim
f(
x
)
A
x
x
0
0
x
x
0
0

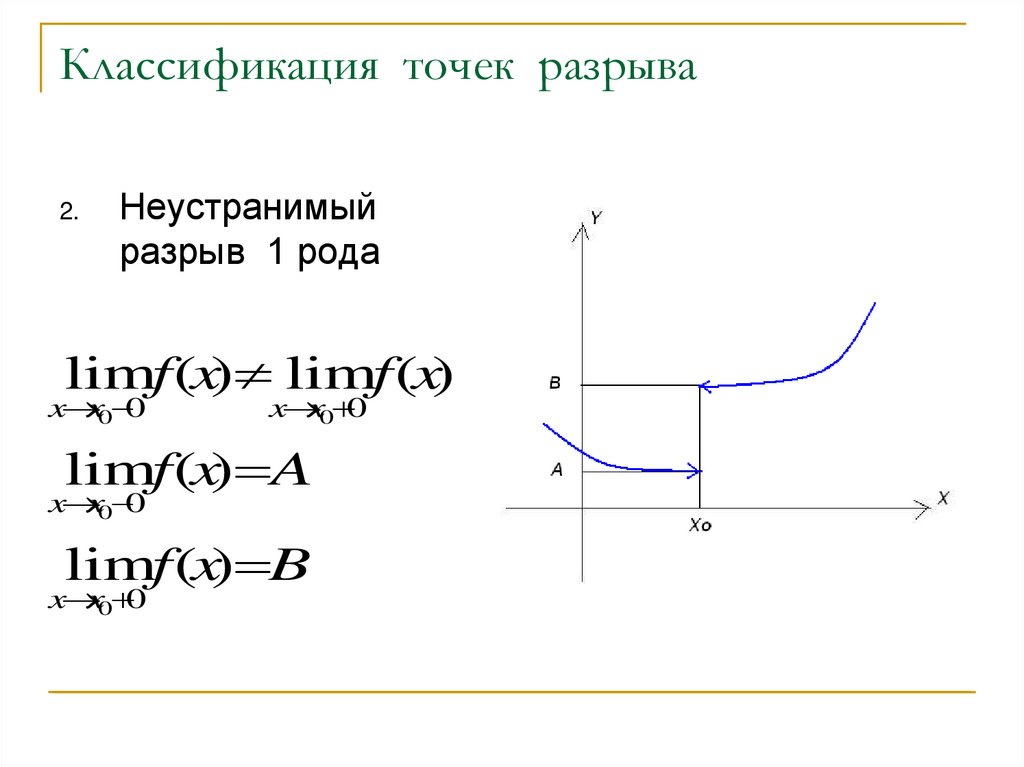
4. Классификация точек разрыва

2.
Неустранимый
разрыв 1 рода
limf (x) limf (x)
x x0 0
x x0 0
limf (x) A
x x0 0
limf (x) B
x x0 0

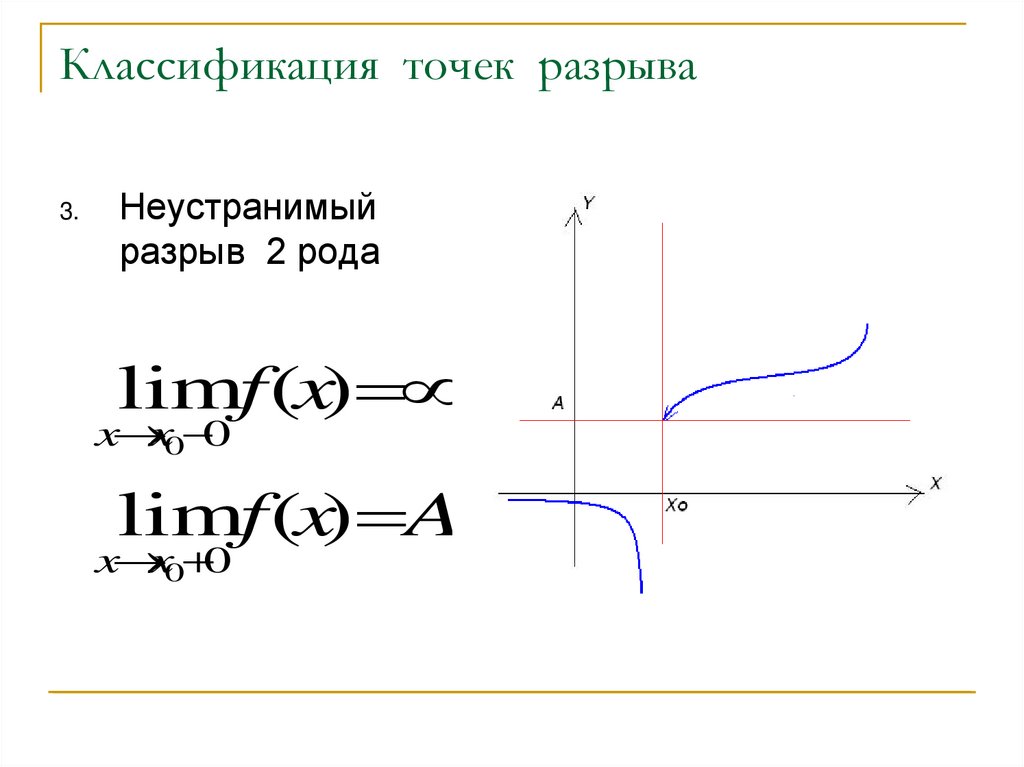
5. Классификация точек разрыва

3.
Неустранимый
разрыв 2 рода
limf (x)
x x0 0
limf (x)
x x0 0

6. Классификация точек разрыва

3.
Неустранимый
разрыв 2 рода
limf (x)
x x0 0
limf (x) A
x x0 0

7. Свойства непрерывных функций

1.
Все основные функции непрерывны в области их
определения.
2.
Функция является непрерывной на интервале (a;
b), если она непрерывна в каждой точке этого
интервала.

8. Свойства непрерывных функций

3.
Если функции f(x) и g(x) непрерывны в x0, то
f(x)+g(x), f(x)-g(x), f(x)g(x), f(x)/g(x)
непрерывны в x0
4.
Функция f(g(x)) – непрерывная.

9. Понятие производной

f
(
x
x
)
f
(
x
)
0
0
y
(
x
)
lim
0
x
0
x

10. Геометрический смысл производной

y
(
x
)
tg
k
0
M
M
0

11.

Если функции u=u(х) и v=v(х) дифференцируемы в точке х, тогда
справедливы следующие правила дифференцирования:
Здесь с –постоянная
1.
2.
3.
( cu ) c u
(u v ) u v
(u v ) u v v u
u v v u
u
4.
v2
v
5. Пусть функция у=f(u), где u=u(х). Тогда у есть сложная функция от
х: y=f(u(x)), а u — промежуточный аргумент. Производная от
сложной функции находят по правилу
dy
y ( x)
y (u ) u ( x)
dx
или
dy dy du
dx du dx

12. Таблица основных формул дифференцирования

1.
y c, y 0, c
- постоянная
2.
y x , y x 1 .
3.
y a x , y a x ln a; y e x , y e x .
4.
y log a x, y
5.
y sin x, y cos x.
6.
y tgx, y
1
.
x ln a
y cos x, y sin x.
1
.
2
cos x
1
.
7. y ctgx, y
2
sin x