Похожие презентации:
Множество комплексных чисел
1.
Множествокомплексных
чисел.
2.
Комплексным числом называется выражениевида а + bi, в котором а и b – действительные числа,
а i – некоторый символ такой, что
i
1
Действительное число a называется действительной
2
частью z=a+bi (Re z), а число b-мнимой частью (Im z)
Комплексное число z=a+bi изображают точкой
плоскости с координатами (a;b)
Точка М(a;b), соответствующая комплексному числу
z=a+bi, называется аффиксом данного числа z.
3.
Два комплексных числа (a; b) и (c; d) называютсяравными, если а = с и b = d.
Комплексное число a-bi называется
комплексно сопряженным с числом a+bi
z
и обозначается через
z a bi= a-bi
Комплексные числа вида a+bi и –a-bi называются
противоположными.
4.
Арифметические операции надкомплексными числами
Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1 z2=
a+bi
c+di
=
ac−bd
+(ad+bc)i
Сумма двух комплексных чисел z1=a+bi и z2=c+di
будет комплексное число вида
z=z1+z2=a+bi+c+di=a+c+(b+d)i
Разностью двух комплексных чисел z1=a+bi и
z2=c+di будет комплексное число вида
z=z1−z2=a+bi−c+di=a−c+(b−d)i
Произведение двух комплексных чисел z1=a+bi и
z2=c+di будет комплексное число вида
z=z1*z2=(a+bi)*(c+di) =ac−bd+(ad+bc)i
5. Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z2/z1= (a+bi)/(c+di)= (ac+bd)/(c2+d2)+(bc−ad)*i
/(c2+d2)6. Нахождение степеней числа i
Если показатель степени i делится на 4, тозначение степени равно 1, если при делении
показателя на 4 в остатке получается 1, то
значение степени равно i, если при делении
показателя на 4 остаток равен 2, то значение
степени равно -1, если в остатке при делении
показателя на 4 будет 3, то значение степени
равно –i.
7.
• Вычислить: 1) iРешение:
1) i66
66
, 2) i143 , 3) i216 ,4)i137
66:4=16(2). Остаток равен 2, значит i66=-1
2)i143
143 :4=35(3).В остатке 3, значит i 143=-i
,
3)i216
216:4=54(0).в остатке 0, значит i216=1
4)i137
137:4=34(1).В остатке 1, значит i137=i
8.
Пример 1Вычислить:
3 2
i
(
1
2
i)i
1
i
9.
1)(
1
2
i)i
i
2
i
2
i
2
3
2
i (3
2
i)(
1
i) 3
2
i
3
i
2
i 3
5
i
215
2
)
i
2
1
i (
1
i)(
1
i)
1
i
1
1 22
2
15 53
3
)(
2
i)
i
i
22 22
10.
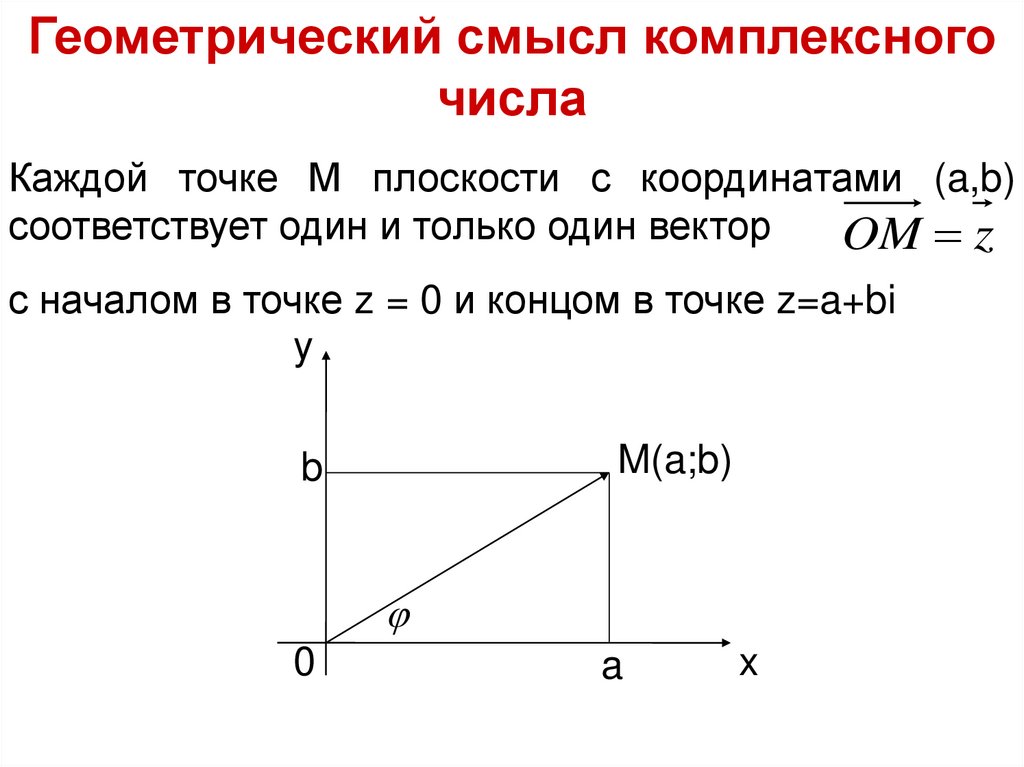
Геометрический смысл комплексногочисла
Каждой точке М плоскости с координатами (a,b)
соответствует один и только один вектор
OM z
с началом в точке z = 0 и концом в точке z=a+bi
y
M(a;b)
b
0
a
x
11.
Если комплексное число Z= a+bi трактовать какточку M (a,b) плоскости xOy, то модуль Z равен
расстоянию точки M (a,b) от начала координат
z a b
2
2
Если на плоскости ввести полярные координаты
(r,φ), где φ аргумент числа z (φ=argz) - угол
между действительной осью ОХ и вектором ОМ,
то а = r COS φ, b = r SIN φ
В силу этого комплексное число Z можно
записать в форме z = r(COS φ+iSIN φ),
где r – модуль числа Z, φ – угол (в рад.), который
составляет вектор OM с положительным
направлением оси ox
12.
Тригонометрическая формакомплексного числа
Тригонометрической формой комплексного числа
называют его запись в виде:
z = r(cosφ + isinφ), где r a2 b2 - модуль, а
φ – аргумент числа z, связанный с а и b формулами:
cos
sin
a
a b
b
2
2
a2 b2
;
Угол φ из промежутка ; называется главным
аргументом. Все остальные значения угла φ могут быть
получены прибавлением к главному аргументу значений
2 n, где n – любое целое число.
13.
Пример2.Записать в тригонометрической форме:
Сначала находим модуль числа:
r (
23
)
2
4
2
Далее, согласно формулам (*),
имеем:
2
3 3
2
1
cos
;
sin
4 2
4
2
Учитывая, что угол
2 3 2i
; 5
5
5
Итак, z
4
cos
isin
6
6
6
2
14.
Действия над комплексными числами,заданными в тригонометрической форме
При умножении/делении комплексных чисел,
заданных в тригонометрической форме, их модули
перемножаются /делятся, а аргументы складываются
(вычитаются).
z
z
r
r
(cos(
)
i
sin(
))
1
2
1
2
1
2
1
2
(1)
z
1 r
1
(cos(
)
i
sin(
))
1
2
1
2
z
(2)
2 r
2
15.
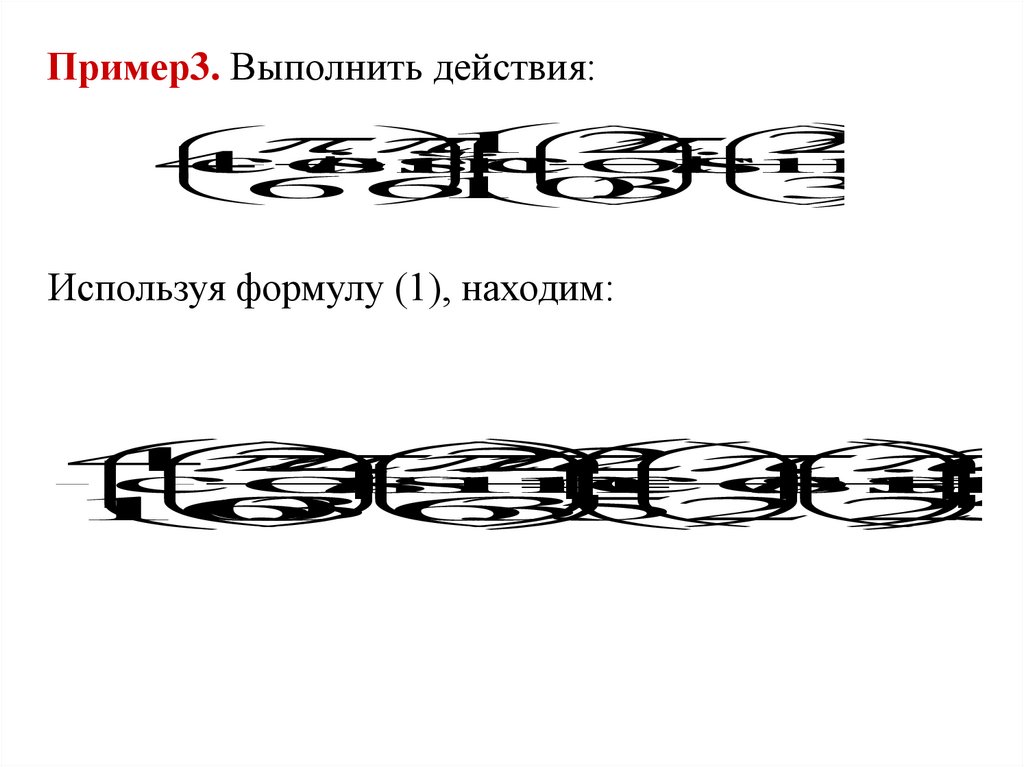
Пример3. Выполнить действия:1
2
2
4
cos
i
sin
*
cos
i
sin
10
3
3
6 6
Используя формулу (1), находим:
4
2
2
2
2
cos
i
sin
cos
i
sin
i
10
6
3
6
3
5
2
2
5
16.
При возведении комплексного числаz = r (Cosφ + iSinφ) в натуральную степень
n
модуль данного числа возводится в эту
степень,
а аргумент умножается на показатель степени:
формула Муавра
z r (cos n i sin n )
n
n
17.
Корень n-й степени из комплексногочисла z = r (Cosφ + iSinφ) имеет n различных
значений, которые находятся по формуле :
n
2
2
z r cos
i sin
n
n
n
Здесь к = 0, 1, 2, … n-1
18.
Пример4. Решить уравнениеz 4 0
2
Корнями данного уравнения являются все значения
Для числа - 4 имеем r =2,
2
Согласно формуле,
находим:
2
2
4 2 cos
i sin
2
2
Если к = 0, то 1
2 cos i sin
2
2
2i
3
3
i sin
2i
Если к = 1, то 2 2 cos
2
2
4
19.
Показательная форма комплексногочисла. Формула Эйлера
Если комплексному числу(cos i sin )
, модуль которого равен 1, поставить в соответствие
показанное выражение e i , то получим соотношение
i
cos i sin e ,
то получим соотношение которое называется формулой
Эйлераz.
Любое комплексное число можно записать в
виде
z re
i
Эта форма записи комплексного числа
называется показательной формой.
.
20.
Пример: Записать числов показательной
форме.
3
3
z 3(cos
i sin
)
2
2
3
Решение: Здесь r 3,
2
тогда показательная форма числа имеет вид
.
z 3e
3
i
2
21.
Пример: Записать число z 5i в показательнойформе.
z
Решение. Что бы представить число
в виде
z
z re
i
нужно найти модуль и аргумент числа
3
2
2
2
,
Здесьa 0, b 5; тогда r a b 0 5 5,
2
лежит на мнимой оси комплексной плоскости.
так как точка
r и
.
Зная
z
, получим
.
z 5e
3
i
2
22.
•Действия над комплексными числами,заданными в показательной форме
Если комплексные числа записаны в показательной
форме, то умножение, деление, возведение в степень
производится по правилам действий со степенями.
Так, для произведения и частного комплексных чисел
i 2
i 1
и
z 2 r2 e справедливы формулы
z re
1
1
z1 z 2 r1 r2 e
i 1 2
z1
r1
e i 1 2
z2
r2
а для n-й степени комплексного числа используется
n
n i n
•формула z
r e
23.
Для вычисления корня из комплексного числаz re
i
используется формула
2 k
n
z re
n
n
где k принимает n значений: 0,1,2,…,n-1.
24. Понятие функции комплексного переменного и отличие от действительного анализа
Пусть D – некоторая область на комплексной плоскостиОпределение. Функцией комплексного аргумента с
областью определения D называется соответствие,которое
любому комплексному числу
сопостовляет
z D
одно или несколько комплексных значений.
Таким образом, в отличие от действительного анализа, в
комплексном анализе допускаются многозначные функции.
Например,
f(z)=az+b (a, b – фиксированные комплексные числа)однозначная функция;
f ( z ) z 2 - однозначная функция
25.
f ( z)n
z - n-значная функция;
f ( z ) Argz -бесконечнозначная функция.
Если функция однозначна,то она может быть
задана в виде отображения f : D C В таком
случае функция называется однолистной .В
дальнейшем, если не указано особо,будем
рассматривать однолистные функции.
26.
Пример: Для функцииz2 1
f ( z)
1найти
2i
f (i )
Решение: Подставим в место z значение i в функцию
i 1
1 1
f (i)
1
1 0 1 1
2i
2i
2
Ответ:
f(i)=1
27. Компоненты функции
Пусть дана функция , f (z ) z D Представим z вz x iy Значение f(x)алгебраической форме
f ( z ) C,которое также можем
комплексное число,т.е.
f ( z ) u ( z ) iv,где
( z)
представить в алгебраической форме
u (z-действительные
)
v( z )
и
функции комплексного
аргумента,но задание я эквивалентно заданию
пары(x,y).Окончательно,любую функцию комплексного
аргумента можно представить в виде
f ( z ) u ( x, y ) iv ( x, y ),где
и v ( x, y ) действительные функции двух действительных
переменных.Функции u и v называются компонентами
функции f(z),u- действительная компонента,v-мнимая
компонента.Пишут :
u ( x, y )
u Re f ( z ) v Im f ( z )
28.
f ( z ) ( x iy ) 4i2
Пример: Для функции
z x iy
Где
мнимую часть.
найти ее действительную и
Решение:
(x+iy)2+4i=x2+2ixy-y2+4i=(x2-y2)+(2xyi+4i)=(x2-y2)+i(2xy+4).
Тогда действительная часть функции f(z) - x2-y2,а
мнимая - 2xy+4.
Re( f ( z )) x y
2
2
Im( f ( z )) 2 xy 4
29.
Понятие непрерывности определяется аналогичнодействительному случаю.
f ( z) f ( z0 ) 0 ( )
z0 lim
z z
z z0 f ( z) f ( z0 )
Так как это определение
формально совпадает с обычным ,то все свойства
непрерывной функции комплексного аргумента
совпадают дословно со свойствами действительных
функций.
F(z)-непрерывна в точке
0








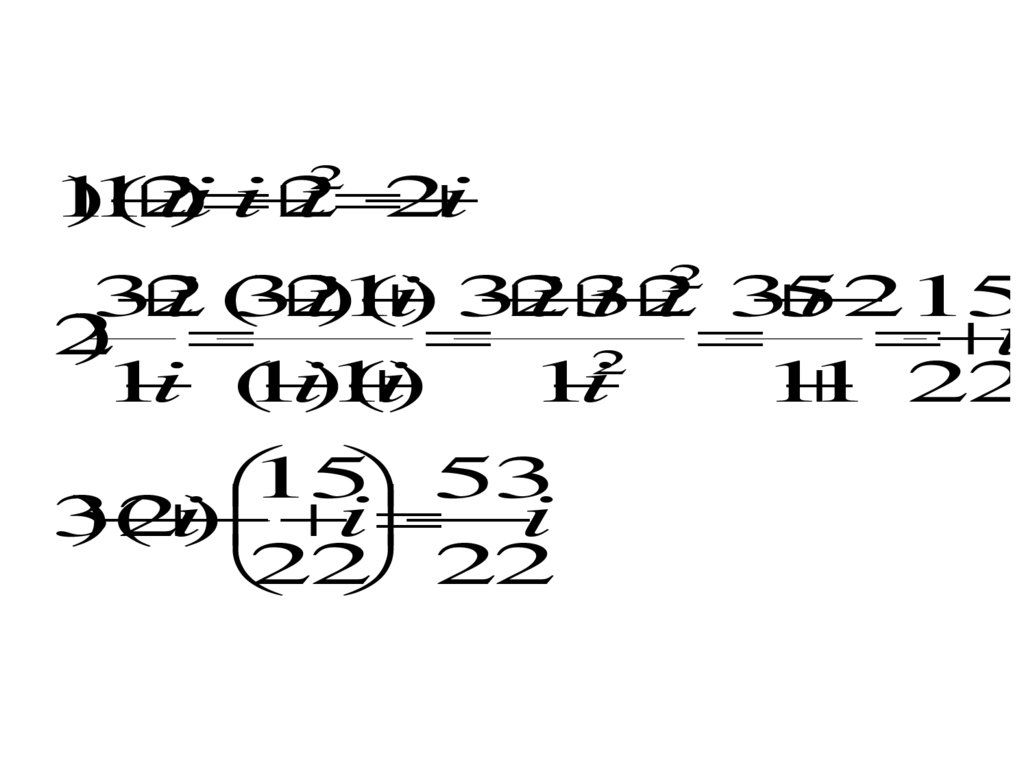


















 Математика
Математика








