Похожие презентации:
Рациональные дроби и их свойства
1. Рациональные дроби и их свойства
mathvideourok.moy.su2. Рациональные выражения
Выражение, составленное из чисел ипеременных с помощью действий сложения,
вычитания, умножения и деления на число,
отличное от нуля называется целыми
выражениями
Например : 7а в; m d ; ( х у )( х у ); в ;
а 5
в(3в с)
10
19;
; 2 х : 9; в
8
7
2
2
3
2
7
3.
Выражение, составленное из чисел,переменных с помощью действий и
деления на выражение с переменными
называется дробным выражением.
3 х у
n
5
Например : ;
; 2 p : с; 2
а х у
3 n 1
Целые и дробные выражения называются
рациональными
4.
1) Найти значение рационального выраженияа 4
, если а 3
а 2
2
9 4 5
1
3 2 5
2) Найти значение рационального выражения
3а 1
, если а 4
а 4
12 1 11
4 4
0
не имеет смысла
на 0 делить нельзя, значит а 4 недопустимое
значение для этой дроби
5.
Целое выражение имеет смысл всегда.Дробное не всегда имеет смысл( на нуль
делить нельзя)!!!
1
3
2)
;х 4
Например :1) ; а 0
х 4
а
3к
3
к
3) 2
; к любое 4) 2
; к 2
к 2
к 4
1
1
5)
;
х 4 х 5
х 4; 5
6.
Значения переменных, при которыхвыражения имеют смысл называют
допустимыми значениями переменных
а
рациональная дробь
в
Найти допустимые значения переменной
дроби:
5
1)
;
а(а 3)
а любое число, кроме 0;3
а(а 3) 0
а 0; а 3 0
а 3
7.
( х 2) 252)
; х любое число, кроме 3
2х 6
2
2х 6 0
2 х 6
х 3
а
Дробь 0 тогда и только тогда,
в
когда а 0; в 0
8.
Узнаем когда дробь равна 0( х 2) 25
0
2х 6
2
( х 2) 25 0
2
( х 2) 25
х 2 5; х 2 5
х 5 2 х 5 2
2
х 3
2х 6 0
2 х 6
х 3
х 7
Ответ : при х 7
9. Формулы:
(а в) а 2ав в2
2
2
(а в) а 2ав в
2
2
2
а в (а в)(а в)
3
3
2
2
а в (а в)(а ав в )
3
3
2
2
а в (а в)(а ав в )
2
2
10. Основное свойство дроби. Сокращение дробей
Если числитель и знаменатель дробиумножить или разделить на один и тот
же не равный нулю многочлен, то
получится равная ей дробь.
х 2 ( х 2)а
1)
х 3 ( х 3)а
2х
2)
4у
х
2у
11.
Если числитель и знаменательрациональной дроби разделить на один и
тот же не равный нулю многочлен, то
получится равная ей дробь. Данную
операцию называют сокращение дробей
21у 7
5 ху
у
4)
1)
3 ух х
10 хк 2 к
а в
а в
3
3( х 3)
5)
1
2)
в а
а в
4а( х 3) 4а
2
а 9 (а 3)(а 3) а 3
3)
в(а 3)
в
ав 3в
12.
Равенство, которое получается присокращении дробей или при умножении
числителя и знаменателя на один и тот
же не равный нулю многочлен
называется тождеством.
1) Приведите дробь к знаменателю 35 у
2 х 10 ху 2
3
7у
35 у
3
2)Приведите дробь к знаменателю х-4к
3
3
4к х
х 4к
13.
3) Сократите дробь:2
2
а в
(
а
в
)(
а
ав
в
)
а
в
а
в
2
2
а ав в
а 2 ав в 2
1
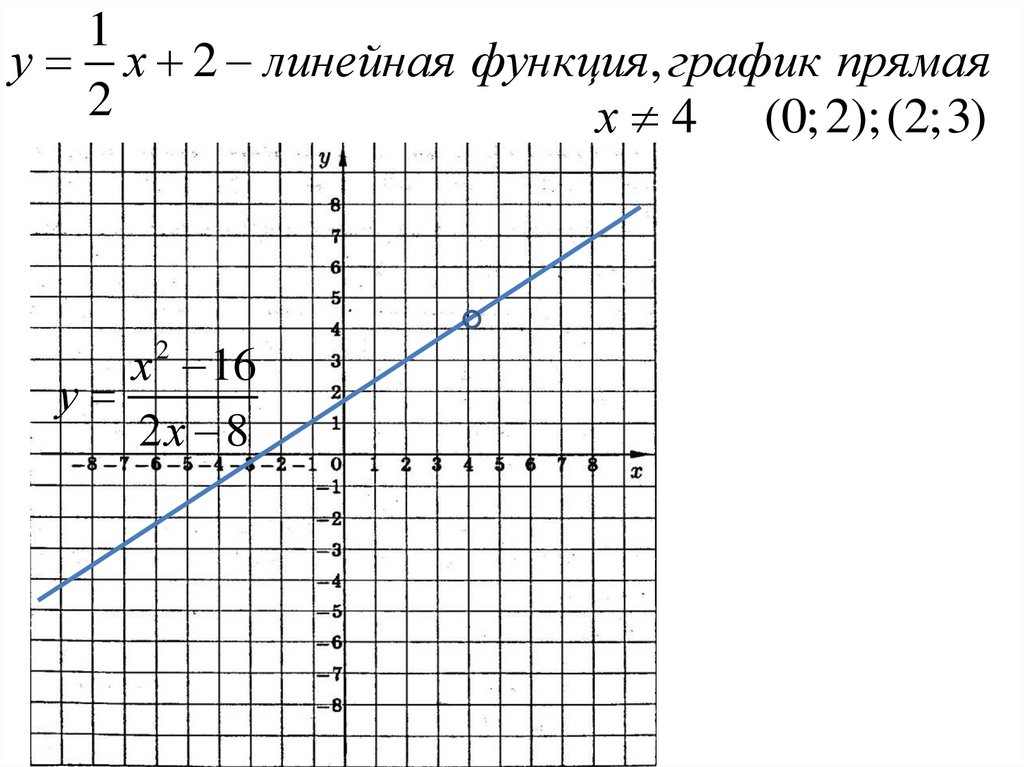
4) Постройте график функции:
2
х 4 1
х 16 ( х 4)( х 4)
х 2
у
2( х 4)
2
2х 8
2
3
3
2х 8 0
2х 8
х 4
14.
1у х 2 линейная функция, график прямая
2
х 4 (0; 2);(2;3)
х 2 16
у
2х 8













 Математика
Математика