Рациональные дроби

1.

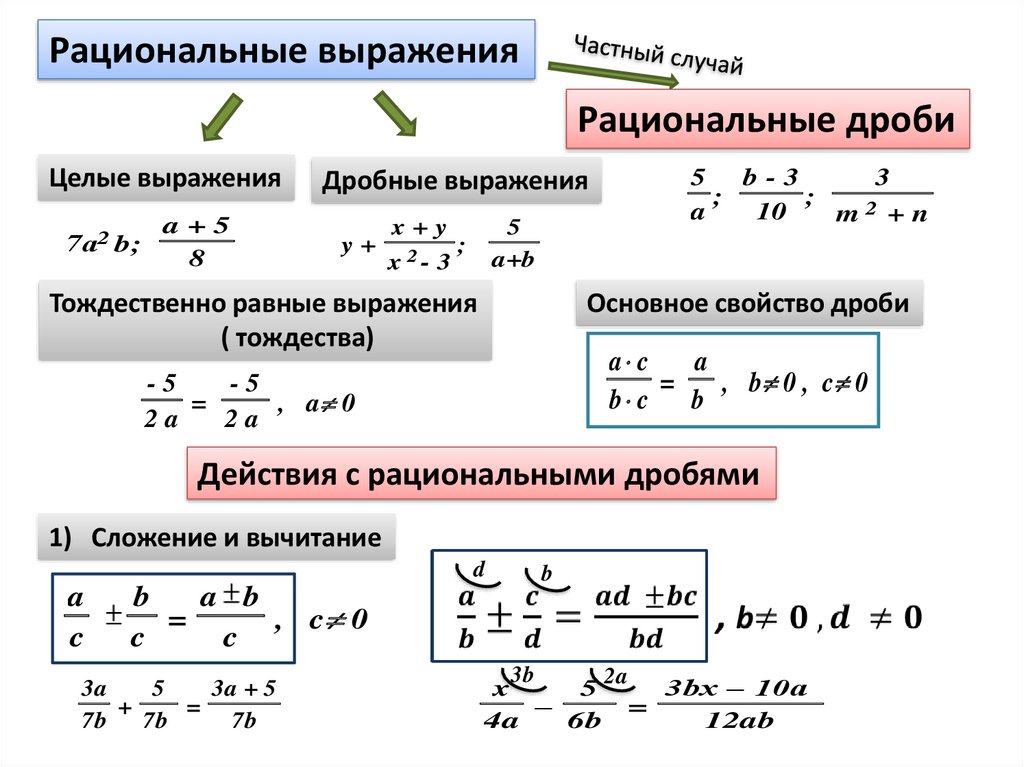
Рациональные выражения
Рациональные дроби
Целые выражения
7а2 b;
a+5
8
Дробные выражения
y+
x+y
;
x 2- 3
5
a+b
Тождественно равные выражения
( тождества)
5
b-3
3
;
;
a
10
m2 + n
Основное свойство дроби
a c
a
=
, b 0 , c 0
b c
b
-5
-5
=
, a 0
2a
2a
Действия с рациональными дробями
1) Сложение и вычитание
d
a
c
b
b
a b
=
, c 0
c
c
3a
5
3a + 5
+
=
7b
7b
7b
3b
2a
x
5
3bx – 10a
–
=
4a
6b
12ab

2.

2) Умножение и деление
a c
a c
=
, b 0 , d 0
b d
b d
5
6
5 2
10
=
=
3b x
1 b x bx
a c a d
: =
, b 0 , c 0 , d 0
b d b c
10 5c 10 3
2 1
2
:
=
=
=
3b 3
3b 5c 1 b c bc
3) Возведение произведения и дроби в степень
( a b
)n
( 5 x ) 3
=
=5
a n
3 x 3
bn
= 125x 3
a n an
( ) = n , b 0
b
b
3 2
32
9
( ) = 2 = 2
x
x
x

3.

Определение. Выражение, составленное из чисел и переменных с
помощью действий сложения, вычитания, умножения,
а также деления на число, отличное от нуля, называется
целым выражением. Если выражение помимо действий
сложения, вычитания и умножения содержит деление на
выражение с переменной, то это выражение называется
дробным выражением.
Целые и дробные выражения называют рациональными
выражениями.
Определение. Дробь, числитель и знаменатель которой многочлены,
называется рациональной дробью.
Определение. Значения переменных, при которых выражение имеет смысл
называют допустимыми значениями переменных
Основное
Если числитель и знаменатель рациональной дроби
свойство
умножить на один и тот же ненулевой многочлен, то
дроби
получится равная ей дробь.
Определение. Тождеством называется равенство, верное при всех
допустимых значениях входящих в него переменных.

4.

Правило. Чтобы сложить две рациональные дроби с одинаковыми знаменателями,
надо сложить их числители, а знаменатель оставить тем же.
Правило. Чтобы выполнить вычитание рациональных дробей с одинаковыми
знаменателями, надо из числителя первой дроби вычесть числитель
второй дроби, а знаменатель оставить тем же.
Правило. Чтобы сложить две дроби с разными знаменателями надо привести дроби
к наименьшему общему знаменателю и сложить полученные дроби с
одинаковыми знаменателями.
Правило. Чтобы выполнить вычитание рациональных дробей с разными
знаменателями, надо привести дроби к наименьшему общему знаменателю
и выполнить вычитание полученных дробей с одинаковыми знаменателями.
Правило. Чтобы умножить дробь на дробь, надо перемножить их числители,
перемножить их знаменатели и первое произведение записать числителем,
а второе - знаменателем дроби.
Правило. Чтобы разделить одну дробь на другую, надо первую дробь умножить
на дробь, обратную второй.
Правило. Чтобы возвести произведение в степень, надо возвести в эту степень
каждый множитель.
Правило. Чтобы возвести дробь в степень, надо возвести в эту степень числитель и
знаменатель, первый результат записать в числителе, а второй – в
знаменателе дроби.