Похожие презентации:
Решение задач с помощью линейных уравнений
1. Решение задач с помощью линейных уравнений
2.
УСТНАЯ РАБОТА1 ряд
Уравнение
2 ряд
Корень Буква
Уравнение
3 ряд
Корень Буква
Уравнение
Корень
–9x – 56 = 5x
–9x – 56 = 5x
–9x – 56 = 5x
40 – 12x = 20 – 11x
40 – 12x = 20 – 11x
40 – 12x = 20 – 11x
15 – 8x = 2 – 9x
15 – 8x = 2 – 9x
15 – 8x = 2 – 9x
63 – 8n = n
63 – 8n = n
63 – 8n = n
15x – 12 = 8 + 10x
15x – 12 = 8 + 10x
15x – 12 = 8 + 10x
–10y – 64 = –6y
–10y – 64 = –6y
–10y – 64 = –6y
25 – 9y = 5y + 11
25 – 9y = 5y + 11
25 – 9y = 5y + 11
8 – 5n = 10 – 4n
8 – 5n = 10 – 4n
8 – 5n = 10 – 4n
Корень -13
2
ПРОВЕРЬТЕ!
20
4
Г
Буква
Г
Л
И
-16
Корень
4
3
-2 -36
Р
Буква
А
Ф
О М
Буква
Т
Е
Н
Корень
-4
-2
1
Буква
И
Л
А
Корень -20
5 -10 -5
7
Р
Буква
Корень
1
40 -2
Буква
С
Т
Э НЕН
Корень 14
5
-4
6
К
А
П
О
Буква
19
3. Найди ОШИБКУ
3а)
б)
(7х + 1) – (6х + 3)= 5
7х + 1 – 6х +– 3 = 5
7х – 6х = 5 –+ 1 +– 3
х = 78
0,7(х – 4) = 0,6(х + 9) – 6,7
0,7х ––0,28
2,8 ==0,6х
0,6х++0,54
5,4 ––6,7
6,7
0,7х – 0,6х = 5,4 +– 6,7 + 2,8
0,1х = 1,5
х = 1,5
0,1 : 0,1
1,5
х = 15
1,5
4.
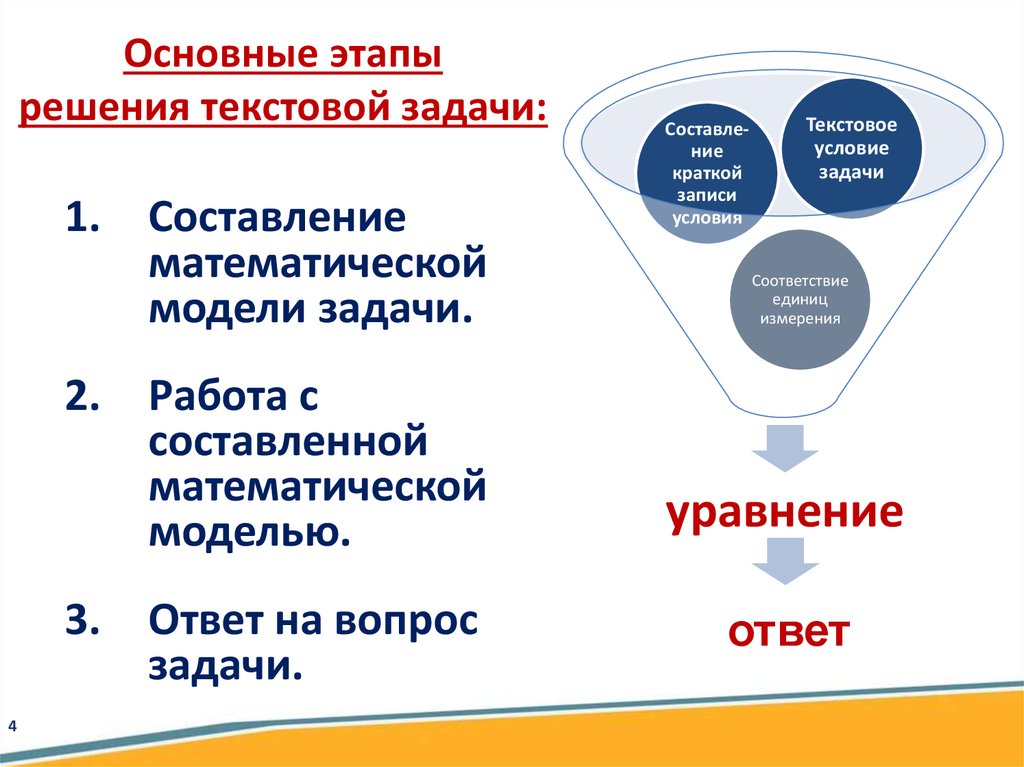
Основные этапырешения текстовой задачи:
1. Составление
математической
модели задачи.
2. Работа с
составленной
математической
моделью.
3. Ответ на вопрос
задачи.
4
Составление
краткой
записи
условия
Текстовое
условие
задачи
Соответствие
единиц
измерения
уравнение
ответ
5.
Основные типы задач:Задачи «о движении»
Автомашина за 3,5 ч проехала на 10 км
Скорость (v)
Время (t)
Расстояние (s)
больше,
чем мотоцикл
за 2,5 ч.
Скорость
мотоцикла на 20 км/ч больше, чем
I
скорость автомашины. Найдите скорость
автомашины
и скорость мотоцикла.
II
Основные соотношения:
1) Единицы измерения должны соответствовать
друг другу: м/с, с, м ; км/ч, ч, км.
Например, перевод минут в часы: а мин = а/60 ч !
2) v × t = s t = s / v , v = s / t
5
6.
Основные типы задач:Задачи «о движении по реке»
Лодка проплыла от одной пристани до
Вид движения
Скорость
(v) Времяреки
(t) Расстояние
другой
против
течения
за 4 (s)
ч.
Обратный
у нее 3 ч. Скорость
По течению путьХзанял
+У
течения
реки
1
км/ч.
Найдите
Против течения
У
собственную Х –скорость
лодки
и
Собственная
Х пристанями.
расстояние между
Течение
У
Основные соотношения:
1) и 2) – такие же
3) v(по течению) = v(собственная) + v(течения)
v(против течения) = v(собственная) – v(течения)
6
7.
Основные типы задач:Задачи «о совместной работе»
Через первую Производительность
трубу бассейн можно
Время (t)
Работа (q)
труда (w)
заполнить за 20 ч, а через
вторую - за 30
1
ч.работник
За сколько часов наполнится бассейн
через
обе эти трубы?
2 работник
Вместе
Основные соотношения:
1) Единицы измерения времени – любые (одинаковые!)
2) t × w = q t = q / w , w = q / t
3) w(1) + w(2) = w(Вместе)
4) Вся работа = 1 или 100%.
7
8.
Основные типы задач:Задачи «о планировании»
Чтобы выполнить
задание в срок, токарь
Производительность
Время (t)
Работа (q)
труда (w)
должен был изготавливать
по 24 детали в
По
плану Однако он ежедневно перевыполдень.
нял норму на 15 деталей сверх плана и
По
факту
уже
за 6 дней до срока изготовил 21
деталь сверх плана. Сколько деталей
изготовил
токарь?
Основные
соотношения:
1) и 2) – такие же
3) Единицы измерения работы – шт. (количество
единиц продукции)
8
9.
ПРАКТИЧЕСКАЯ РАБОТА9
10.
Проверка№ 1.
Скорость
(v)
Время
(t)
Расстояние (s)
Автомашина
х км/ч
3,5 ч
3,5х км, на 10 км Б
Мотоцикл
х+20 км/ч
2,5 ч
2,5(х+20) км
3,5 х – 10 = 2,5(х + 20)
или 2,5(х + 20) + 10 = 3,5 х
или 3,5 х – 2,5(х + 20) = 10
10
11.
Проверка№ 2.
Вид движения
Скорость (v) Время (t) Расстояние (s)
Против течения
х – 1 км/ч
4ч
4(х – 1) км
По течению
х + 1 км/ч
3ч
3(х + 1) км
Собственная
х км/ч
Течение
1 км/ч
4(х – 1) = 3 (х + 10)
11
12.
Проверка№ 3.
Производительность
Время (t)
Работа (q)
труда (w)
1 труба
20 ч
1/20
1
2 труба
30 ч
1/30
1
Вместе
х ч
1/20 + 1/30
1
1
1
х 1
20 30
12
13.
Проверка№ 4.
ПроизводиВремя
тельность
(t)
труда (w)
Работа (q)
По плану
х дней
24 дет
24х дет
По факту
х–6
дней
39 дет
39(х-6) , на 21 дет Б
39(х – 6) – 21 = 24х
13
14.
Другие типы задачНекоторые формулы:
P▄ = 2(a + b)
S▄ = a∙b
a
P■ = 4a
S■ = a2
- плотность,
V - объём
a
S▲ = ah/2
a
14
m = ∙V,
m – масса,
b
h
1% = 0,01
a% от числа b =
= 0,01a ∙b
15.
Другие способы оформления условиях+5
х
Р = 50
2(х + х + 5) = 50
15
16.
Другие способы оформления условия№ 1.
v1=х км/ч, t1=3,5 ч
s1=3,5х км
s2=2,5(х+20) км
10 км
v2=(х+20) км/ч, t2= 2,5 ч
2,5(х + 20) + 10 = 3,5 х
a
16
17.
Решите задачу № 5:В первом мешке в 2 раза больше муки, чем во
втором. Когда из первого мешка взяли 30 кг
муки, а во второй добавили 5 кг, то во
втором стало муки в 1,5 раза больше, чем в
первом. Сколько килограммов муки в двух
мешках первоначально?
было
I мешок – 2х кг
II мешок – х кг
cтало
2х - 30 (кг)
?
х + 5 (кг); в 1,5 раза >, чем
1,5 (2х – 30) = х + 5
17
ОТВЕТ: 75 кг
18.
Презентация создана учителем МОУ «СОШ № 1 города БилибиноЧукотского АО» Шрамковой Ольгой Геннадиевной.
СПИСОК ЛИТЕРАТУРЫ:
1. Мордкович А.Г. Алгебра. 7 класс. Учебник для учащихся
общеобразовательных учреждений. – М.: Мнемозина, 2008 г.
2. Крамор В.С., Повторяем и систематизируем школьный курс
алгебры и начал анализа. – М.: Просвещение, 1990 г.
3. Использовались иллюстрации с сайта http://office.microsoft.com
18
19. Решение задач с помощью линейных уравнений
20. Задача № 1
• Саша решал две задачи за 35 минут.Первую задачу он решал на 7 мин. дольше,
чем вторую. Сколько минут Саша решал
вторую задачу?
20
21. Задача № 2
• В первом мешке в 3 раза большекартофеля, чем во втором. После того как
из первого мешка взяли 30 кг картофеля, а
во второй насыпали еще 10 кг, в обоих
мешках картофеля стало поровну. Сколько
кг картофеля было в двух мешках
первоначально?
21
22. Домашнее задание:
1. Длина отрезка АС 60 см. Точка В взята на отрезке АСтак, что длина отрезка АВ в 4 раза больше длины
отрезка ВС. Найдите длину отрезка ВС.
2. В первом контейнере в 5 раз больше моркови, чем
во втором. Когда из первого контейнера взяли 25 кг
моркови, а во второй засыпали еще 15 кг, то в обоих
контейнерах моркови стало поровну. Сколько кг
моркови было в двух контейнерах первоначально?
3. стр. 35, контрольные вопросы и задания (в
отдельных тетрадях)
22





















 Математика
Математика