Похожие презентации:
Индексный метод
1. Индексный метод
ИНДЕКСНЫЙ МЕТОД2.
ИндексОтносительный показатель сравнения состояния
простого или сложного явления, состоящего из
соизмеримых или несоизмеримых элементов, во
времени или пространстве.
3. Задачи индексного метода
Оценкадинамики
Анализ
влияния
факторов
Анализ
влияния
структурных
сдвигов
Оценка
территориальных
сравнений
4. Классификация индексов
5.
По степениохвата
Индивидуаль
ные
Общие
(сводные)
Групповые
6.
По базесравнения
Динамические
Цепны
е
Базисные
Индексы
выполнения
плана
Территориальные
7.
По виду весовС постоянными весами
Стандартные
Отчетного
периода
Базисного
периода
С переменными весами
8.
По форме построенияАгрегатные
Средние взвешенные
Гармонические
Арифметические
9.
По составуявления
Переменны
е
Постоянные
10.
Основнойэлемент
индексного
отношения- индексируемая величина.
Индексируемая величина – значение
признака
статистической
совокупности,
изменение
которой
является изучается.
11.
Терминология и символика:q – количество (объем) какого-либо продукта в
натуральном выражении (от лат. quantitas);
p- цена единицы товара (от лат. pretium);
pq – общая стоимость проданных товаров данного
вида (товарооборот, выручка).
Подстрочные знаки:
1 – для сравниваемых (текущих, отчетных) периодов;
0 – для периодов, с которыми проводится сравнение.
Индивидуальные индексы: iq индивидуальный индекс
объема произведенной продукции отдельного вида
или количества проданного товара данного вида.
ip - индивидуальный индекс цен.
12.
• Характеризует динамикууровня изучаемого
явления во времени за
сравниваемые периоды
или выражает
Индивидуальный соотношение отдельных
индекс
элементов совокупности
13.
Индивидуальные индексы определяютвычислением отношения двух индексируемых
величин
14. Основные формулы для вычисления индексов
ИндексИндекс физического объема продукции
Индекс цен
Индекс стоимости продукции
Индекс себестоимости
Основная
формула
q
iq 1
i p p1
i pq
p2
p1q1
p0 q0
z
iz 1
izq
Индекс затрат на производство
q0
z0
z1q1
z 0 q0
15.
Общийиндекс
Характеризует
обобщающие
результаты
совместного
изменения всех
единиц, образующих
статистическую
совокупность
16. Формы общих индексов
Агрегатная
Средняя
арифметичес
кая
Средняя
гармоническа
я
17. Элементы агрегатного индекса
Индексируемая величина• Признак, изменение которого
характеризует индекс
Вес индекса
• Величина, тесно связанная с
индексируемой величиной и
служащая для целей
соизмерения индексируемых
величин
18.
I pqqp
q p
1 1
0
0
Этот индекс показывает, во сколько раз
возросла (уменьшилась) стоимость
продукции (товарооборота) отчетного
периода по сравнению с базисным или
сколько процентов составляет рост
(снижение) стоимости продукции.
19. Индекс Пааше
I pqqp
q
p
1 1
1
0
20.
qpгде
1
- фактическая стоимость
товаров (товарооборот) отчетного
периода;
q p
1
1
0
- условная стоимость
товаров, реализованных в отчетном
периоде по базисным ценам.
21.
Рассчитанный по формуле общий индекс ценпоказывает, во сколько раз возрос (уменьшился) в
среднем уровень цен на массу товара,
реализованную в отчетном периоде, или сколько
процентов составляет его рост (снижение) в
отчетном периоде по сравнению с базисным
периодом.
22. Функции агрегатных индексов
• Обобщениенепосредственно
Синтетичес
несоизмеримых
кая
явлений
• Измерение
Аналитичес
влияния
отдельных
кая
факторов на
совокупное
изменение
23.
Средний
индекс
Индекс,
вычисленный как
средняя величина
из
индивидуальных
индексов
24.
К исчислению таких индексов прибегаюттогда, когда имеющаяся в распоряжении
информация не позволяет рассчитать
общий агрегатный индекс.
25. Средний арифметический индекс количества
nq1
q
i 1
0
I
n
26. Средний арифметический индекс Пааше
IП
p
i
p
q
p 01
p
q
01
27. Средний гармонический индекс Пааше
pq
1 1
П
Ip
p1q1
i
p
28.
Индекспеременн
ого
состава
Индекс,
выражающий
соотношение
средних уровней
изучаемого явления
29.
xIx
x0
x f x f
f f
1 1
0 0
1
0
30.
Индекспеременного
состава
представляет собой отношение двух
взвешенных средних с изменяющимися
(переменными) весами, показывающее
изменение
индексируемой
средней
величины.
31.
Индекспостоянно
го состава
характеризует
динамику средней
величины при одной
и той же
фиксированной
структуре
совокупности
32. Индекс постоянного состава
Ixx f
f
1 1
1
x f
f
0
1
1
33.
Индекс постоянного состава показывает,как в отчетном периоде по сравнению с
базисным изменилось среднее значение
показателя по какой-либо однородной
совокупности за счет изменения только
самой индексируемой величины, т.е.
когда влияние структурного фактора
устранено.
34.
Индексструктурны
х сдвигов
измеряет влияние
только
структурных
изменений на
исследуемый
средний
показатель
35. Индекс структурных сдвигов
I стрx f x f
f f
0 1
0 0
1
0
36.
Индекс структурных сдвиговопределяют как отношение среднего
уровня индексируемого показателя
базисного периода, рассчитанного на
отчетную структуру, к фактической
средней этого показателя в базисном
периоде:
37.
Междуиндексами
переменного,
постоянного составов и индексом
структурных
сдвигов
существует
следующая взаимосвязь
I x I x I стр
т.е.
индекс
переменного
состава
выступает как произведение двух
индексов:
индекса
постоянного
состава
и
индекса
структурных
сдвигов.



















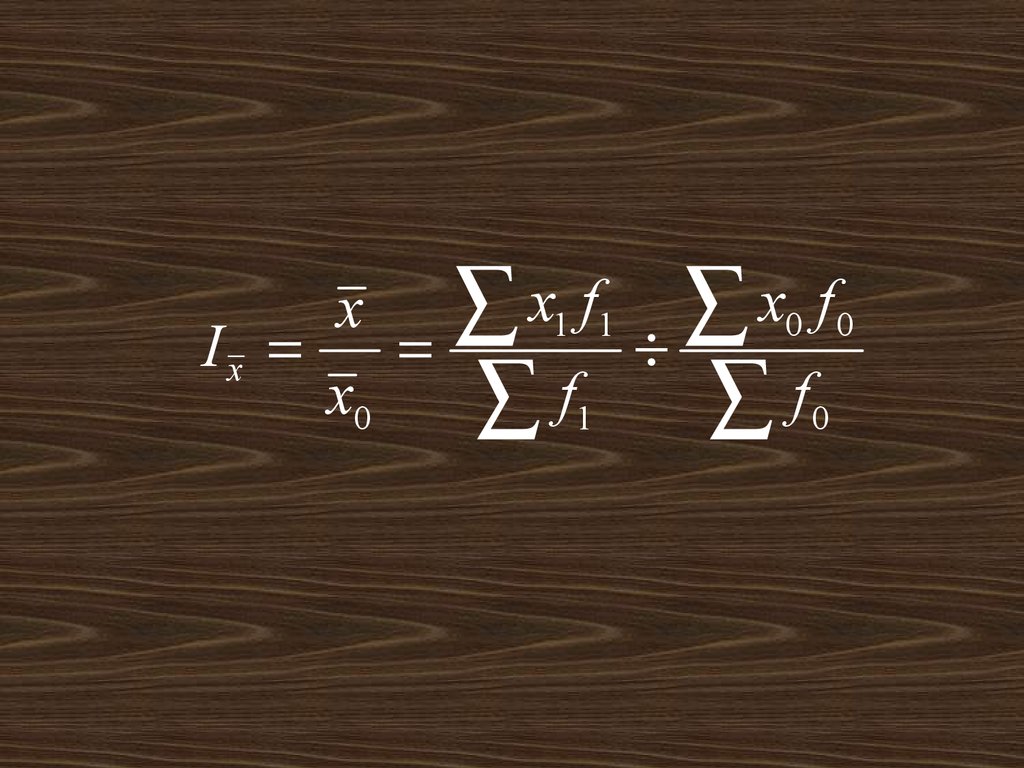






 Экономика
Экономика








