Индексный метод в статистике

1.

Индексный метод в
статистике
Тема 8

2.

Вопросы:
1. Индексы и их классификация.
2. Индивидуальные индексы.
3. Агрегатные индексы.
4. Средние индексы.
5. Индексы постоянного, переменного
состава и структурных сдвигов.
6. Цепные и базисные индексы

3.

1. Индексы и их классификация

4.

Статистический индекс – это относительная
величина, показывающая, во сколько раз
уровень изучаемого явления в данных
условиях отличается от уровня того же
явления в других условиях
Статистический индекс используется для
сравнения сложных совокупностей и
отдельных их единиц

5.

Основным элементом индексного
отношения является индексируемая
величина.
Под индексируемой величиной
понимается значение признака
статистической совокупности,
которая является объектом
изучения.

6.

С помощью индексов решаются три
главные задачи:
1. Индексы позволяют определять изменение
сложных явлений, т.е. исследуют сложные
совокупности.
2. С помощью индексов можно определить
влияние отдельных факторов на изменение
динамики сложного явления (например, влияние
уровня цен и изменения количества проданных
товаров на объем товарооборота).
3. Индексы являются показателями сравнений
не только с прошлым периодом (во времени), но и с
другой территорией (сравнение в пространстве), а
также с нормативами, планами, прогнозами

7.

Индексы классифицируются по трем
признакам:
1) по характеру изучаемых объектов;
2) по степени охвата единиц
совокупности;
3) по методам расчета общих
индексов

8.

По характеру изучаемых объектов
Индексы количественных показателей:
индексы физического объема
продукции;
индексы розничного товарооборота;
индексы национального дохода и др.
Индексы качественных показателей:
индексы курса валют;
индексы цен, себестоимости,
производительности труда;
индексы средней заработной платы;
индексы урожайности

9.

По степени охвата единиц совокупности
индексы делятся на два класса:
индивидуальные и общие
Индивидуальные индексы характеризуют
изменение отдельных единиц совокупности.
Общий индекс отражает изменение всех
элементов сложного явления.
Если индексы охватывают не все элементы
сложного явления, а лишь часть, то их
называют групповыми или субиндексами
(индексы продукции по отдельным отраслям
промышленности).

10.

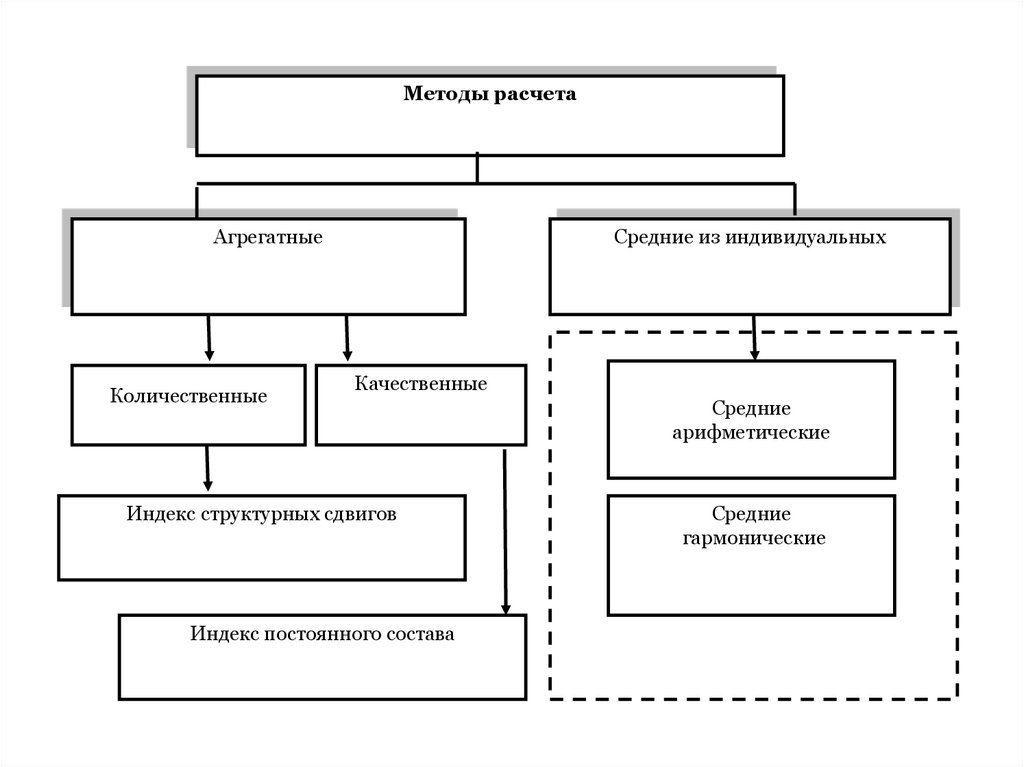
Методы расчета
Агрегатные
Количественные
Средние из индивидуальных
Качественные
Индекс структурных сдвигов
Индекс постоянного состава
Средние
арифметические
Средние
гармонические

11.

Обозначения в теме:
i
I
q
p
с
t
pq
1
0
- индивидуальный индекс;
- общий индекс:
- количество (объем) какого-либо продукта в натуральном
выражении;
- цена единицы продукции;
- себестоимость единицы продукции;
- затраты времени на производство единицы продукции
(трудоемкость);
- общая стоимость произведённой продукции данного вида или
товарооборот, выручка.
Подстрочные знаки индексов:
- для сравнимых (текущих) периодов;
- для периодов, с которыми производится сравнение (базисных).

12.

2. Индивидуальные
индексы

13.

Индивидуальные индексы
характеризуют соотношение
уровней только одного элемента
совокупности (например, рост или
падение цен).

14.

Индивидуальный индекс физического объёма продукции iq
рассчитывается по формуле:
q1
iq
q0
или
iq
q
q
1
,
(8.1)
0
где q1, q0 - количество продукции соответственно в отчетном и
базисном периоде в натуральном выражении.
Индекс физического объема продукции показывает, во
сколько раз изменился физический объем продукции или на
сколько процентов составляет его рост (снижение) в отчетном
периоде по сравнению с базисным.

15.

Индивидуальный индекс цен ip рассчитывается по формуле:
p
ip 1
p0
ip
p
p
1
0 ,
или
(8.2)
где р1, p0 – цена единицы продукции соответственно в отчетном и
базисном периоде.

16.

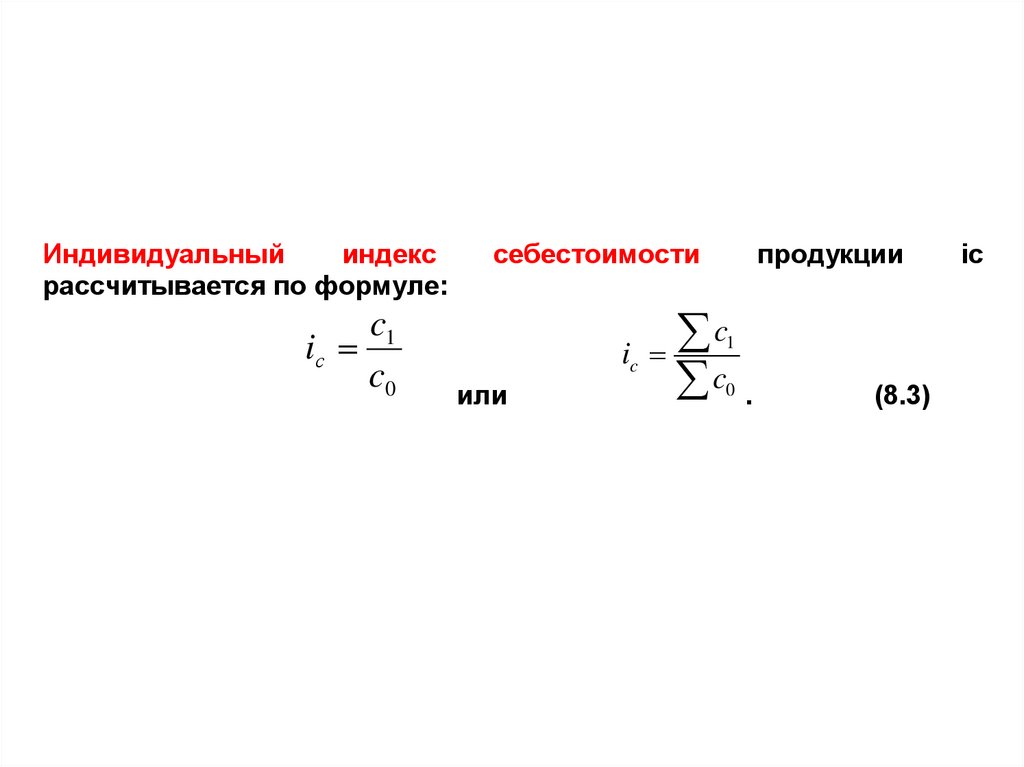
Индивидуальный
индекс
рассчитывается по формуле:
c1
iс
c0
себестоимости
ic
или
продукции
c
c
1
0
.
(8.3)
ic

17.

Индивидуальный индекс товарооборота
(стоимости товарооборота) ipq рассчитывается по формуле:
i pq
p1q1
p0 q0
i pq
или
pq
p q
1 1
0 0
.
(8.4)

18.

Одной из важнейших особенностей индивидуальных индексов
является следующее утверждение:
какое соотношение между показателями индексируемых величин,
такое соотношение и между индексами этих показателей:
i pq i p i q
.
(8.5)

19.

20.

Одной из важнейших особенностей индивидуальных индексов
является следующее утверждение:
какое соотношение между показателями индексируемых величин,
такое соотношение и между индексами этих показателей:
i pq i p i q
.
(8.5)

21.

3. Агрегатные индексы

22.

Агрегатный индекс – это основная и наиболее
распространенная форма индекса.
Его числитель и знаменатель представляют
собой набор – «агрегат» (от латинского –
складываемый, суммируемый)
несоизмеримых и неподдающихся
суммированию элементов – сумму
произведений двух величин, одна из которых
меняется (индексируется), а другая остается
неизменной в числителе и знаменателе
индекса (соизмеритель или вес индекса).

23.

Агрегатные индексы выполняют синтетическую и
аналитическую функции.
Синтетическая функция характеризуется тем, что в
одном индексе обобщаются непосредственно
несоизмеримые явления.
Аналитическая функция следует из взаимосвязи
индексов.

24.

Агрегатные индексы количественных
показателей
В агрегатных индексах количественных показателей в
качестве индексируемой величины используется
количественный показатель, а весом индекса
(соизмерителем) выбирается качественный показатель.
При этом количественный показатель в числителе и
знаменателе индекса принимается на разных уровнях
(индексируется), а вес индекса – на одном неизменном
временном уровне.

25.

Общий
продукции
индекс
физического
(реализованной
объема
продукции)
определяют по формуле:
Iq
где
q
q
1
pi
0
pi
,
(8.6)
q1 , q0 – объем продукции каждого вида
изделий соответственно отчетного и базисного
периодов (индексируемый показатель);
pi
– цена отдельных видов продукции в i-м
периоде (вес индекса).

26.

Если
уровне
соизмеритель
базисного
индекса
периода,
то
принимается
исчисляют
на
индекс
Ласпейреса:
Iq
q
q
1
p0
0
p0
.
(8.7)
В числителе данного индекса – условная стоимость
произведенной в отчетном периоде продукции в ценах
базисного периода.
В
знаменателе
–
фактическая
продукции базисного периода.
стоимость

27.

Абсолютное
изменение
физического
объема
продукции можно определить следующим образом:
qpq q1 p0 q0 p0 .
Экономически
сколько
денежных
продукции
в
эта
разность
единиц
результате
(8.8)
показывает,
изменилась
роста
или
на
стоимость
снижения
ее
физического объема, то есть количества проданных
товаров.

28.

Индексы качественных показателей
В
агрегатных
индексируемой
индексах
величиной
качественных
является
показателей
качественный
показатель, а весом индекса (соизмерителем) выбирается
количественный
показатель.
При
этом
качественный
показатель в числителе и знаменателе индекса принимается
на разных уровнях (индексируется), а вес индекса – на одном
неизменном временном уровне.
К
индексы
индексам
цен,
качественных
себестоимости,
производительности труда и т.п.
показателей
трудоемкости
относятся
продукции,

29.

Поскольку
индексируемой
индекс
характеризует
величиной
изменение
является
цена,
а
цен,
то
весом
–
количество товаров одного из периодов.
Сводный индекс цен определяют по формуле:
Ip
p q
p q
1
0
где
p1 , p0
соответственно
–
цена
в
отчетном
i
,
(8.9)
i`
отдельных
и
видов
базисном
продукции
периодах
(индексируемый показатель);
qi – объем реализованной продукции в i-м периоде (вес
индекса).
Данный индекс характеризует, как изменились цены в
среднем на различные виды продукции в анализируемой
совокупности.

30.

Формула агрегатного индекса цен Ласпейреса представляет
собой следующее соотношение:
,
(8.10)
p1q0 - условная стоимость товаров, которые
где
реализованы в базисном периоде по отчетным ценам;
p q
0 0
- фактическая стоимость продукции базисного
периода.
Индекс Ласпейреса показывает, на сколько изменились
цены в отчетном периоде по сравнению с базисным, но по той
продукции, которая была реализована в базисном периоде.

31.

В 1874 году немецкий экономист Г.Пааше впервые предложил
агрегатный индекс цен с отчетными весами.
Формула
агрегатного
индекса
цен
Пааше
выглядит
следующим образом:
Ip
p1q1
где
отчетного периода;
pq
p q
1 1
0 1
-
,
фактическая
(8.11)
стоимость
продукции
p q
- условная стоимость товаров, которые
реализованы в отчетном периоде по базисным ценам.
0 1
Индекс цен Пааше показывает, во сколько раз возрос
или уменьшился в среднем уровень цен на массу товара,
реализованную в отчетном периоде, или на сколько процентов
составляет его рост или снижение в отчетном периоде по
сравнению с базисным периодом.

32.

Индекс цен Пааше характеризует, на сколько товары в
отчетном периоде стали дороже либо дешевле, чем в базисном.
При таком методе, рассчитав индекс цен,
определить экономический эффект от изменения цен:
p
pq p1q1 p0 q1
.
можно
(8.12)
Данная разность определяет абсолютную экономию (перерасход)
денежных средств в результате изменения цен на товары

33.

Товар
ы
А, кг
Б, л
В, шт.
Количество
проданных
товаров, тыс.
январ феврал
ь
ь
q0
q1
200
240
60
50
800
650
Цена за единицу
товара, руб.
январь
p0
980
1450
400
феврал
ь
p1
1000
1500
420
Индивидуальны
е индексы цен
1,020
1,035
1,050
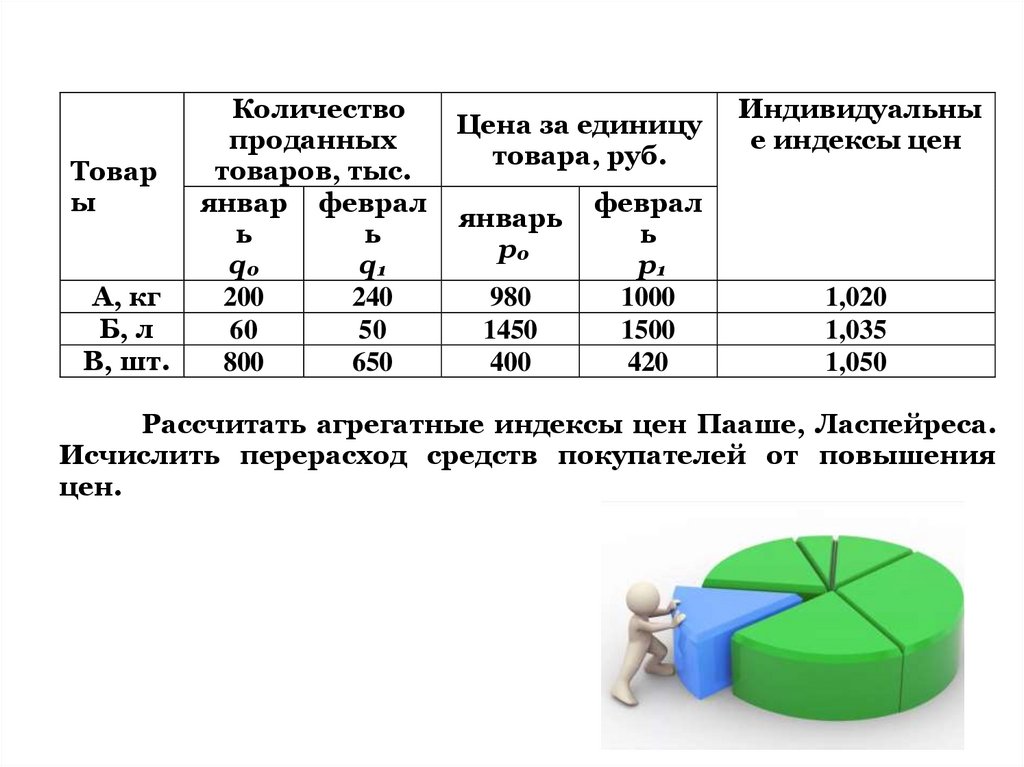
Рассчитать агрегатные индексы цен Пааше, Ласпейреса.
Исчислить перерасход средств покупателей от повышения
цен.

34.

Агрегатный индекс цен Пааше:
I
п
p
pq
p q
1 1
0 1
1000 240 1500 50 420 650 588000
1,036
980 240 1450 50 400 650 567700
Индекс показывает, что в феврале по сравнению с
январём цены на рынке возросли в среднем на 3,6%.
Из-за
средств:
повышения
цен
покупатели
перерасходовали
p
pq 588000 567700 20300тыс. руб. 20,3млн. руб

35.

Агрегатный индекс цен Ласпейреса
I pл
pq
p q
1 0
0
0
1000 200 1500 60 420 800 626000
1,038.
980 200 1450 60 400 800 603000
Индекс показывает, что цены в феврале по сравнению с
январём (не на все продукты, а только на январскую группу)
повысились в среднем на 3,8%.
Условный (т.е. только на январскую группу) перерасход
средств покупателей от повышения цен составил:
p
pq p1q0 p0 q0 626000 603000 23000тыс. руб. 23млн. руб.

36.

Вид
изделия
А
Б
В
Базисный период
объем
цена за 1
продажи, т
кг, руб.,
q0
р0
2,6
14,1
5,5
52
1,5
31
Отчетный период
объем
цена за 1
продажи, т
кг, руб.
q1
р1
1,2
210
1,6
173
0,7
116
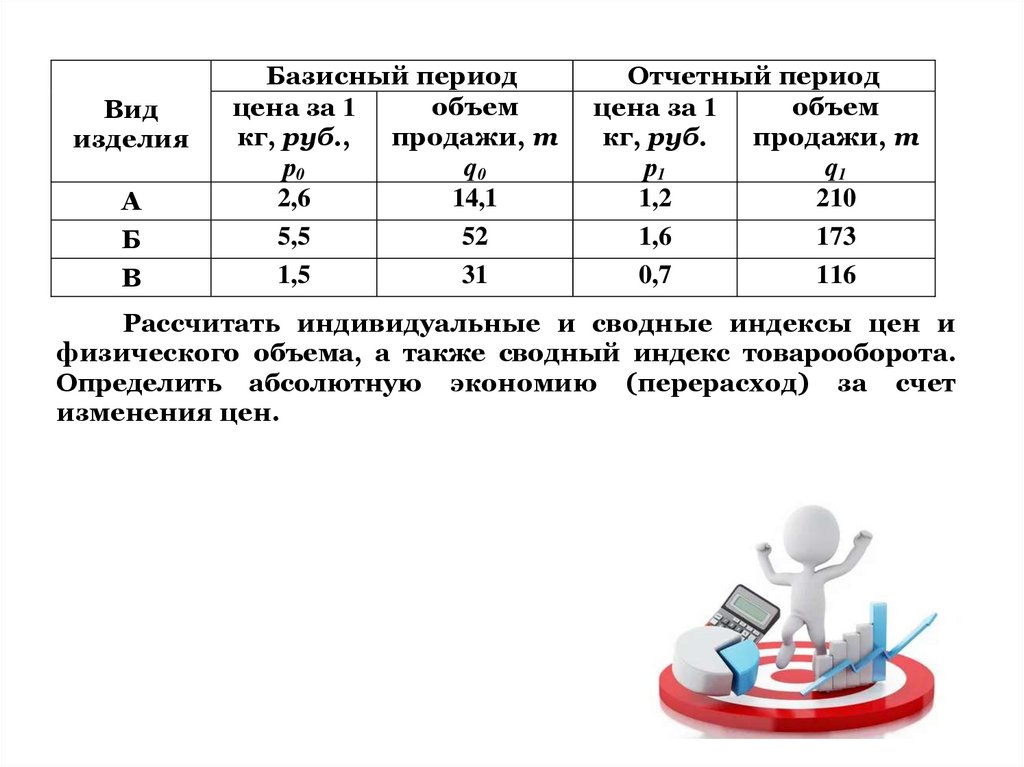
Рассчитать индивидуальные и сводные индексы цен и
физического объема, а также сводный индекс товарооборота.
Определить абсолютную экономию (перерасход) за счет
изменения цен.

37.

Для изделия А индивидуальный индекс цен составит:
p
,
2
11
А: i
0
,
461
или
46
,
1
%.
p
p
2
,
6
0
Это означает, что цена снизилась на 53,9 % (100 – 46,1).
Индивидуальный индекс физического объема изделия А:
q
210
q
141
0
1
А: i
1
,
49
или
149
%.
q
Прирост физического объема составил 49 % (149 – 100).
Индекс стоимости товарооборота изделия А:
,
2
210
252
1
11
А: i
0
,
687
или
68
,
7
%,
pq
p
q
p
q
2
,
6
141
366
,
6
0
0
т.е. стоимость товарооборота снизилась на 31,3 %
(100 – 68,7).

38.

Для
оценки
среднего
изменения
цен
по
всему
ассортименту исчислим сводный (агрегатный) индекс цен:
p
q
1
,
2
210
1
,
6
173
0
,
7
116
610
1
1
I
0
,
36
p
p
q
2
,
6
210
5
,
5
173
1
,
5
116
167
0
1
или 36,5 %, т.е. цена в среднем снизилась на 63,5 %.
Размер экономии покупателей от снижения цен составил:
p
p
q
p
q
610
1671
1061
ты
.
руб
.
pq
1
1
0
1
Индекс
физического
объема
рассматриваемого ассортимента:
реализации
для
q
p
10
2
,
6
173
5
,
5
116
1
,
5
1671
1
0
I
2
,
391
q
q
p
141
2
,
6
52
5
,
5
31
1
,
5
699
0
0
или 239,1 %, т.е. физический объем реализации возрос в 2,391
раза или на 139,1 %.
Индекс стоимости товарооборота составит:
p
q
1
1 610
I
0
,
873
или
87
,
3
%.
pq
p
q
699
0
0
Это означает, что в результате изменения цен на
отдельные виды товаров и изменения объемов продаж
стоимость товарооборота уменьшилась на 12,7 % или на
699 – 610 = 89 тыс. руб.

39.

Американский
экономист
И.
Фишер
предложил
«идеальный» индекс цен, так называемую идеальную форму
индекса
цен,
который
рассчитывается
как
средняя
геометрическая из двух агрегатных индексов цен Ласпейреса и
Пааше:
Ip I I
л
p
п
p
p q p q .
p q p q
1 0
1 1
0 0
0 1
(8.13)

40.

При синтезировании общего индекса цен вместо
фактического количества товаров (в отчетном или базисном
периоде) в качестве соизмерителей индексируемых величин
могут применяться средние величины реализации товаров за
два периода или более.
При таком способе расчета формула общего индекса
преобразуется и имеет вид:
Ip
pq
p q
1
,
(8.14)
0
q
где
- среднее значение количества
реализованных за анализируемый период.
товаров,

41.

Название формул
индексов
Индекс Ласпейреса
(по базисным
весам)
Индекс Пааше
(по отчетным
весам)
Индекс Фишера
Индекс Лоу
(по средним весам)
Формулы индексов
индекс
индекс цен
физического
объема
Iq
Iq
Iq
q p
q p
q p
q p
1
0
0
0
1
1
0
1
0 0
0 1
Iq
0
1
1
0
0
0
1
p
0
p
1 1
Ip
1
1
1 0
Ip
q p q p
q p q p
q
q
pq
p q
pq
p q
Ip
pq pq
p q p q
Ip
1 1
1 0
0 1
0
pq
p q
1
0
0

42.

Индекс себестоимости характеризует среднее изменение
себестоимости единицы продукции отчетного периода по
сопоставимому с базисным периодом кругу продукции. Индекс
себестоимости Пааше имеет вид:с q
Iс
,
с q
1 1
(8.16)
0 1
где ∑c1q1 - затраты на производство продукции отчетного
периода;
∑c0q1 - затраты на производство продукции отчетного
периода, если бы себестоимость
оставалась на уровне
базисного.
Индекс себестоимости Ласпейреса имеет вид:
Iс
сq
,
с q
1 0
(8.17)
0 0
где ∑c1q0 - затраты на производство продукции базисного
периода, если бы себестоимость оставалась на уровне
отчетного;
∑ c0q0 - затраты на производство продукции базисного
периода.

43.

Индекс
стоимости
товарооборота
продукции
определяется
отчетного
отношением
периода
к
стоимости
продукции базисного периода:
I pq
pq
p q
1 1
0
.
0
(8.18)
Этот индекс показывает, во сколько раз возросла (или
уменьшилась) стоимость продукции отчетного периода по
сравнению с базисным или сколько процентов составляет рост
(снижение) стоимости продукции. Если из индекса
товарооборота вычесть 100%, то разность (Ipq–100) покажет, на
сколько процентов изменилась стоимость продукции по
сравнению с базисным периодом

44.

С
помощью агрегатных индексов можно рассчитать
абсолютный
прирост
результативного
показателя
по
факторам:
pq p q p q
1
1
0
0
.
(8.19)
Разность показывает, на сколько денежных единиц
изменилась стоимость продукции в текущем периоде по
сравнению с базисным.
Значение индекса товарооборота зависит от двух факторов:
изменения количества продукции (объема) и цен.

45.

Встречаются и другие формулы расчета индексов. Так,
итальянский ученый Р. Карли (1764 г.) вычислил общий индекс
цен как среднюю арифметическую величину из частных
индексов по формуле:
p1
p
0
Ip
n
i
n
p
.
(8.15)

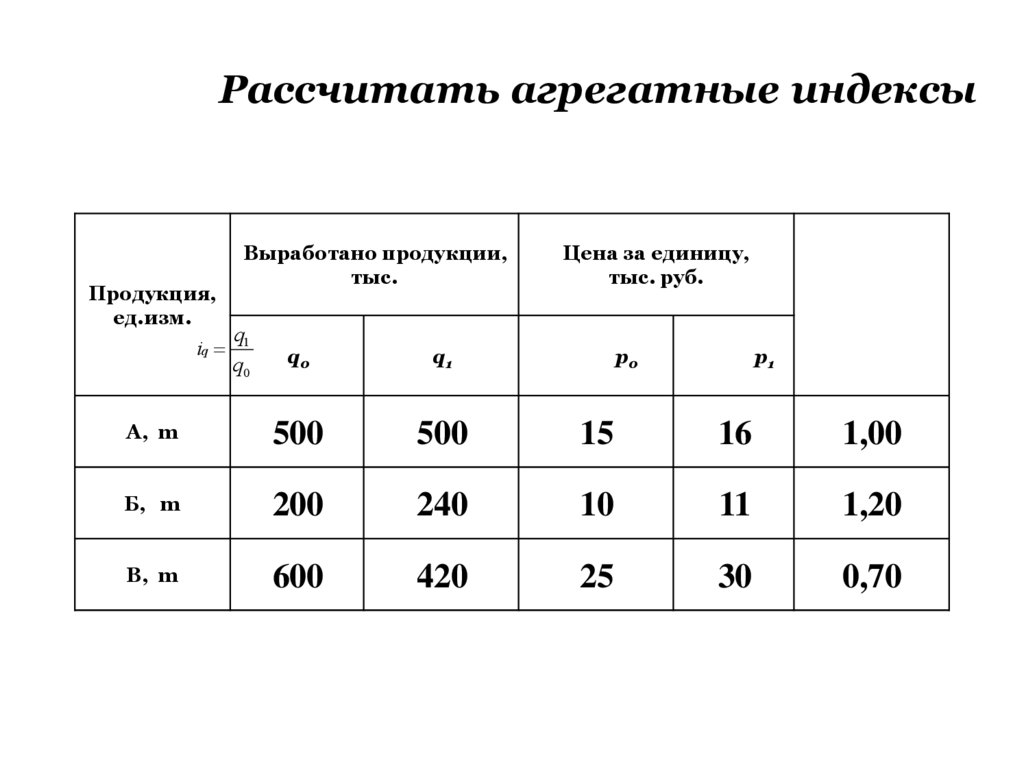
46.

Рассчитать агрегатные индексы
Продукция,
ед.изм.
iq
Выработано продукции,
тыс.
q1
q0
Цена за единицу,
тыс. руб.
q0
q1
p0
p1
A, m
500
500
15
16
1,00
Б, m
200
240
10
11
1,20
B, m
600
420
25
30
0,70

47.

Для определения изменения выпуска всей продукции
рассчитаем общий индекс физического объема продукции:
Iq
qp
q p
1
0
0
0
500 15 240 10 420 25 20400
0,833 или 83,3% .
500 15 200 10 600 25 24500
Физический объем всей продукции в отчетном периоде
составляет 83,3% от его уровня в базисном периоде, он
снизился за это время на 16,7% (0,833 100-100).
Абсолютное
снижение
неизменных ценах, тыс. руб.:
стоимости
продукции
в
pq q1 p0 q0 p0 20400 24500, 4,100
q
т.е. –4,1 млн. руб.
Изменение общего объема продукции в фактических
ценах (с учетом изменения цен) :
I pq
pq
p q
1 1
0
0
500 16 240 11 420 30 23240
0,949 или 94,9%.
24500
24500
Общий выпуск снизился на 5,1% (94,9 - 100).

48.

4. Средние индексы

49.

Приведем пример построения среднеарифметического
индекса физического объема продукции.
Агрегатная форма индекса физического объема с весами
базисного периода (формула Ласпейреса) имеет вид:
I
q p
q p
л
q
.
1
0
0
0
Здесь реальная величина – знаменатель формулы.
i,
Чаще бывают известны индивидуальные индексы
q а
неизвестны количества произведённой продукции в натуральных
единицах.
Преобразования формулы индивидуального индекса физического
объема продукции позволят определить величину физического объема
отчетного периода:
iq
q1
q1 iq q0
.
q0
Подставив в формулу агрегатного индекса найденное значение
получим формулу среднеарифметического индекса:
. Iq
i q p
q p
q
0
0
0
0
(8.16
q1,
Вес – стоимость
товарооборота
отдельных
видов
продукции в базисном
периоде.

50.

Построение среднегармонического индекса представим на
базе агрегатной формы индекса цен Пааше:
I
п
q
qp
q p
1
1
0
1
q1
q1
iq q0 I qп
q0
iq
q p
qp
i
1
1
1
1
q
Среднегармоническая
продукции имеет вид:
Iq
форма
индекса
qp
qp
i
1
1
1
1
q
.
qp
1
.
i *q p
1
1
1
1
q
физического
объема
(8.17)

51.

Продукты
Индивид. индексы
iq
q1
q0
Продано продукции,
млн.руб.
q0p0
А
1,1
300
Б
0,90
250
В
0,75
400

52.

Среднегармонический индекс цен имеет вид:
pq
I
pq
i
.
(8.18)
1 1
1 1
p
Среднеарифметический индекс цен имеет вид:
Ip
p q
i p. p0 q0
0
0
(8.19)

53.

Расчет общего индекса физического объема продукции проведем по
формуле среднеарифметической:
Iq
i pq
p q
q
0
0
0
0
.
1,1 300 0,9 250 0,75 400 855
0,9
300 250 400
950
Ответ: физический объем продукции в среднем снизился
на 10%.

54.

Рассчитать общее изменение цен
Данные о продаже товаров
Товар
Продано,
млн. руб.
p1q1
Изменение
цен, %
А
Б
Итого
186
214
400
+3
+6
-

55.

Рассчитаем
общее
среднегармонической:
I
п
p
pq
p q
1 1
0 1
pq
pq
i
1 1
1 1
p
изменение
цен
по
формуле
186 214
400
1,046
186 214 382,47
1,03 1,06
или 104,6%.
Вывод: цены повысились в среднем
на 4,6% .

56.

5. Индексы постоянного,
переменного состава и
структурных сдвигов

57.

На изменение среднего значения показателя могут
оказывать воздействие одновременно два фактора: изменение
значений усредняемого показателя и изменение структуры
явления. Требуется определить степень влияния этих двух
факторов.
Если в числителе и знаменателе сводного индекса веса
берутся (фиксируются) на уровне одного и того же периода, то
он
называется
индексом
фиксированного
состава
определяется по формуле:
X
f
X
f
X
f
I :
.
f
f
X
f
1
1
0
1
1
1
ф
.
с
.
1
1
0
1
(8.20)
и

58.

Индекс
переменного
состава
представляет
собой
соотношение средних уровней изучаемого явления.
Если индекс постоянного (фиксированного) состава
показывает среднее изменение лишь одной индексируемой
величины, то индекс переменного состава характеризует
общее
изменение
средней
как
в
результате
изменения
индивидуальных значений индексируемой величины, так и в
результате изменения структуры совокупности (весов).
Индекс переменного состава определяют по формуле:
X
f
X
f
I :
X
:
X
.
f
f
1
1
00
п
.
с
.
1
1
0
0
(8.21)

59.

Для
отражения
влияния
изменений
в
структуре
изучаемой совокупности на динамику изучаемого явления
вычисляется индекс структуры (структурных сдвигов) по
формуле:
X
f
X
f
I
:
.
f
f
01
00
c
.
с
.
1
(8.22)
0
Взаимосвязь между индексами
Iп.с. Iф.с.
Iс.с..
(8.23)

60.

При изучении товарооборота используют:
- индекс цен фиксированного состава
Iф.с.
pq
;
pq
1 1
(8.24)
0 1
- индекс переменного состава
p
qp
q
11
00
I
:
р
:
р
;
п
.
с
.
1 0
q
q
1
0
(8.25)
- индекс структурных сдвигов
p
q
p
q
I
:
.
q
q
01
00
1
0
с
.
с
.
(8.26)

61.

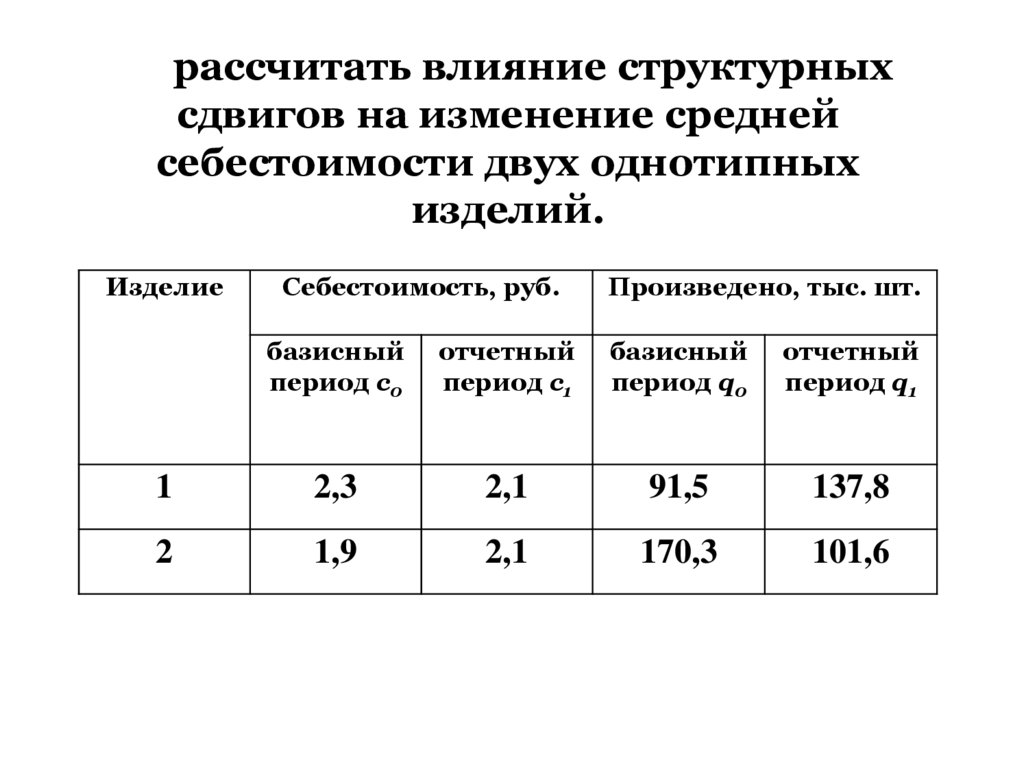
рассчитать влияние структурных
сдвигов на изменение средней
себестоимости двух однотипных
изделий.
Изделие
Себестоимость, руб.
Произведено, тыс. шт.
базисный
период с0
отчетный
период с1
базисный
период q0
отчетный
период q1
1
2,3
2,1
91,5
137,8
2
1,9
2,1
170,3
101,6

62.

Рассчитаем индекс себестоимости переменного состава:
I сп . с .
с q с q
:
q q
1
1
1
0
0
0
с1 : с 0
289,38 213,36 210,45 323,57 502,74 534,02
:
:
1,02
239,4
261,8
239,4 261,8
или 102,9%.
Под
влиянием
изменения
индивидуальных
себестоимостей и структурных сдвигов в производстве данных
изделий средняя себестоимость увеличилась на 2,9 %.

63.

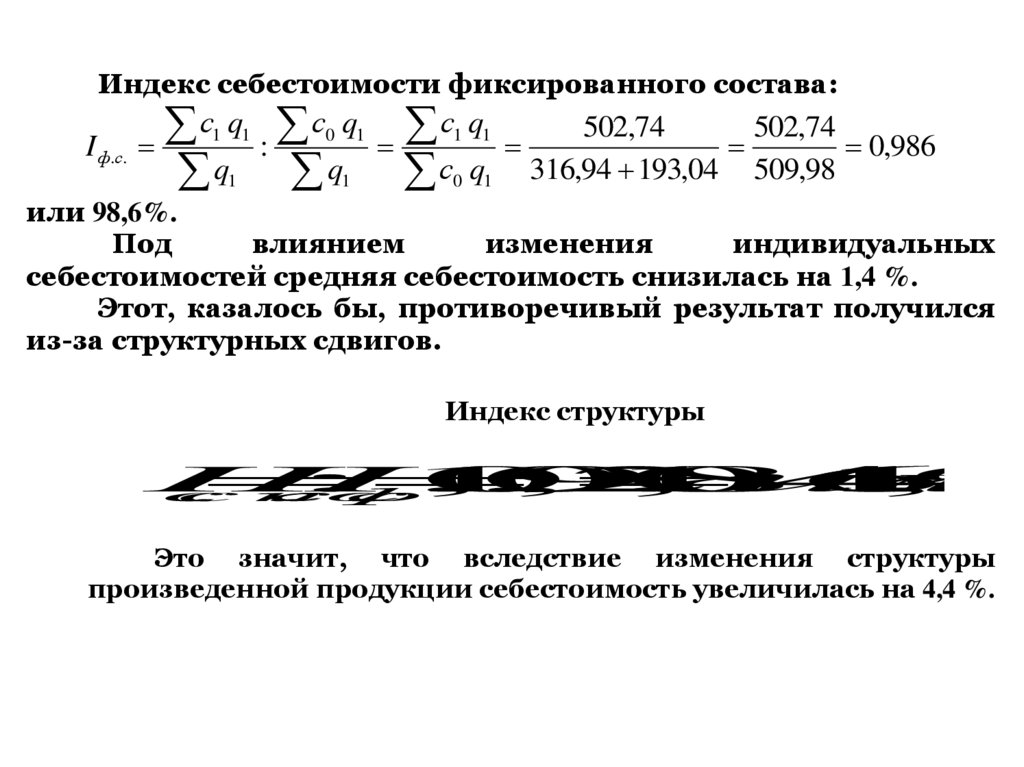
Индекс себестоимости фиксированного состава:
I ф.с.
с q с q
:
q q
1
1
1
0
1
1
с q
с q
1
1
0
1
502,74
502,74
0,986
316,94 193,04 509,98
или 98,6%.
Под
влиянием
изменения
индивидуальных
себестоимостей средняя себестоимость снизилась на 1,4 %.
Этот, казалось бы, противоречивый результат получился
из-за структурных сдвигов.
Индекс структуры
I
I
:
I
1
,
02
:
0
,
986
1
,
044
или
10
,
4
%
c
.
c
. п
.
с
. ф
.
с
.
Это значит, что вследствие изменения структуры
произведенной продукции себестоимость увеличилась на 4,4 %.

64.

6. Цепные и базисные индексы

65.

Цепные индексы представляют собой сравнения
текущих уровней с предшествующими или
непрерывно меняющейся базой сравнения.
Базисные индексы имеют постоянную базу
сравнения, в качестве которой принимаются
данные какого-то одного периода (при анализе
динамики), определенной территории (при
территориальных сравнениях).

66.

1. Отношение базисного индекса отчетного периода к
базисному индексу предшествующего периода дает цепной
индекс отчетного периода:
i p3 / 2 i p3 / 0 : i p 2 / 0 i p3 / 2
p3 p 2 p3
:
p0 p0 p 2
.
2. Произведение последовательных цепных индивидуальных
индексов равно базисному индексу, рассчитанному за последний
период времени:
i p 3 / 0 i p1 / 0 i p 2 / 1 i p 3 / 2
p1 p 2 р3 p3
p0 p1 р 2 p0
.

67.

Контрольные вопросы к теме 7
1. Что называется индексом в статистике?
2. Какие свойства индексов вам известны?
3. По каким признакам классифицируются индексы?
4. Какие виды индексов по содержанию изучаемых величин существуют?
5. Какие виды индексов по степени охвата элементов совокупности существуют?
6. Какие виды индексов по методам расчета вам известны?
7. Какие функции выполняют агрегатные индексы?
8. Что представляет собой индекс потребительских цен (ИПЦ) и какую роль он играет в
экономике?
9. Каким образом могут быть рассчитаны агрегатные индексы цен Пааше, Ласпейреса,
Фишера и Лоу?
10. Что называется индексом себестоимости продукции?
11. Что представляет собой средний гармонический индекс цен?
12. Что представляет собой средний арифметический индекс физического объема
продукции?
13. Что представляют собой индексы постоянного, переменного состава и структурных
сдвигов?
14. Чем характеризуются базисные и цепные индексы?

68.

Спасибо за внимание