Похожие презентации:
Дифференциальные уравнения вида. (Лекция 2.8)
1. Лекция 2.8. 12.1.5. Дифференциальные уравнения вида
Лекция 2.8.12.1.5. Дифференциальные
y¢ = f
уравнения
вида
Рассмотрим два
случая.
æ ax + by + c ö
ç Ax + By + C ÷ .
è
ø
1) Если aB - bA ¹ 0, производят замену переменных
x = x - x0 , y = y - y0 ,
x0 , y0 находятся из решения системы
где
алгебраических уравнений
{
ax + by + c = 0,
Ax + By + C = 0,
cB - bC
aC - cA
x0 = , y0 = .
aB - bA
aB - bA
В результате дифференциальное уравнение сводится к
однородному уравнению.
2. 2) Если производят замену переменных
2) ЕслиaB - bA = 0,
производят замену
переменных
{
x = x,
y = ax + by.
• В результате дифференциальное уравнение
сводится к уравнению с разделяющимися
переменными.
3. Примеры. 1)
-7 x + 3 y - 2y¢ =
.
-3 x + 4 y - 5
aB - bA = -19 ¹ 0.
Первый случай.
-8 + 15 7
35 - 6 29
x0 =
= , y0 =
= .
19
19
19
19
7
ì
ï x = x - 19 ,
í
29
ïy = y - ,
19
î
7
ì
x
=
x
+
,
ï
19
í
29
ïy = y + .
19
î
7 × 7 3 × 29
-7 x + 3 y +
-2
-7 x + 3 y
19
19
¢
y =
=
.
3 × 7 4 × 29
-3 x + 4 y +
- 5 -3 x + 4 y
19
19
Дифференциальное уравнение свелось к
однородному дифференциальному уравнению.
4. 2)
-x + y - 2y¢ =
.
x- y
{
aB - bA = -1( -1) - 1 ×1 = 0.
{
x = x,
x = x,
Второй случай
y = y + x, y¢ = y¢ + 1.
y = - x + y,
Дифференциальное уравнение примет вид
2
y -2 2
или
y¢ = - 2.
y¢ + 1 =
= -1
y
-y
y
Это дифференциальное уравнение с разделяющимися
переменными
( 1 - y - 1) dy
- ydy
1- y
= -2 x + C ,
=
2
dx
+
C
,
ò
y¢ = 2
,
ò 1- y
ò
1- y
y
- x + y + ln 1 + x - y = -2 x + C .
y + ln 1 - y = -2 x + C ,
Окончательно
y + ln 1 + x - y = - x + C.
5. 12.1.6. Линейные дифференциальные уравнения.
Определение. Дифференциальное уравнениеy¢ + p ( x ) y = q ( x ) ,
вида
т.е. линейное относительно неизвестной функции y
ее производной y¢ называется линейным.
и
Для решения такого типа уравнений рассмотрим два
метода: метод Лагранжа и метод Бернулли.
6. Метод Лагранжа (метод вариации произвольной постоянной).
Метод Лагранжа (метод вариации произвольной
y¢ + p ( x ) y = q ( x ) .
постоянной).
Рассмотрим однородное дифференциальное
уравнение y¢ + p ( x ) y = 0. Это уравнение с разделяющимися переменными dy
= - p ( x ) dx, ln y = - ò p ( x ) dx + ln C.
y
- ò p( x ) dx
y
=
Ce
. Общее решение
Решение уравнения
неоднородного линейного дифференциального уравнения имеет такой же вид, но C считается функцией C = C ( x ) ,
- ò p( x ) dx
y
=
C
x
e
.
( )
т.е.
Найдем производную
- ò p( x ) dx
- ò p( x ) dx
¢
¢
y = C ( x) e
- C ( x) e
p ( x)
и подставим в исходное уравнение y и y¢.
C¢( x ) e
- ò p( x ) dx
- C ( x) e
- ò p( x ) dx
p ( x) + p ( x) C ( x) e
- ò p ( x ) dx
= q ( x) ,
7.
C¢ ( x ) e- ò p( x ) dx
C¢( x ) = q ( x ) e
C ( x) = ò q( x) e
= q( x) ,
ò p ( x ) dx
ò p( x ) dx
,
dx + C1.
Общее решение линейного дифференциального
уравнения 1-го порядка имеет вид
y=e
- ò p( x ) dx æ
ç ò q( x) e
è
ò
p ( x ) dx
dx + C1 ö÷ .
ø
8. Метод Бернулли (метод замены переменной).
Метод Бернулли (метод заменыy¢ + p ( x ) y = q ( x ) .
переменной).
Представим неизвестную функцию как произведение
¢.
двух функций y = uv, y¢ = u¢v + uv
Подставим
в исходное
уравнение yи y¢Получим
.
или
u¢v + u v¢ + p x v = q x
¢
¢
u v + uv + p ( x ) uv = q ( x )
Потребуем, чтобы функция была такой, что выражение
v
( v¢ + p ( x ) v )
(
( ) )
тождественно равнялось нулю.
Тогда исходное уравнение сводится к двум уравнениям
с разделяющимися переменными
и
¢
( v¢ + p ( x ) v ) = 0
u v = q ( x) .
( ).
9. Решим их последовательно.
• 1)dv
ò v = - ò p ( x ) dx,
v¢ + p ( x ) v = 0,
ln v = - ò p ( x ) dx,
• 2)
v=e
u¢v = q ( x ) ,
du = q ( x ) e
y=e
ò p ( x ) dx
u¢e
dx,
- ò p( x ) dx æ
- ò p( x ) dx
- ò p ( x ) dx
u = ò q( x) e
ç ò q( x) e
è
ò
p ( x ) dx
ò
.
= q( x) ,
p( x ) dx
dx + C ,
dx + C ö÷ .
ø
10. Уравнение Бернулли.
y¢ + p ( x ) y = q ( x ) y m ,m ¹ 0, m ¹ 1.
Пример. 1) Метод Лагранжа: 3 ( xy¢ + y ) = xy 2 , y ( 1) = 3.
xy¢ + y = 0,
dx
C
dy
dy
dx dy
=
+
ln
C
,
ln
y
=
ln
x
+
ln
C
,
y
=
.
x = - y,
=- , ò
ò
y
x
x
dx
y
x
2
¢
æ
ö
C
x
x
C
x
C
x
C
x)
(
)
(
)
(
)
(
C ( x)
C¢( x ) x - C ( x )
+
=x
,
y=
, y¢ =
. 3ç x
÷
2
2
2
x
x
x
x
è
ø
x
3C ¢ ( x ) =
C2 ( x)
x
,
3ò
dC ( x )
C2 ( x)
=ò
dx
1
+ ln C1, - 3
= ln C1x .
x
C ( x)
3
3
3
1
.
y=, 3=, ln C1 = -1, C1 = e , y = x ( ln x - 1)
x ln C1x
ln C1
11. 1) Метод Бернули:
3 ( xy¢ + y ) = xy 2 , y ( 1) = 3.1) Метод Бернули:
y = uv, y¢ = u ¢v + uv¢.
3 xu ¢v + 3 xuv¢ + 3uv = xu 2v 2 , 3 xu ¢v + 3u xv¢ + v = xu 2v 2 .
(
)
xv¢ + v = 0,
dv
dx
1
ò v = - ò x , ln v = - ln x , v = x .
1
1
2
2
2
3 xu ¢v = xu v , 3 xu ¢ = xu
,
2
x
x
dx
1
+ ln C , - 3 = ln Cx ,
x
u
u2
3
3
3
-1, y = C
=
e
.
y=, 3=, ln C = -1,
x ln Cx
ln C
x ( ln x - 1)
3ò
du
u2
3u ¢ =
,
x
3
u=.
ln Cx
=ò
12. 12.1.7 Дифференциальные уравнения в полных дифференциалах.
Определение. Если левая часть уравненияP ( x, y ) dx + Q ( x, y ) dy = 0
является полным дифференциалом некоторой функции
u ( x, y ) , то это уравнение называется дифференциальным
уравнением в полных дифференциалах.
Это выполняется, если P ( x, y ) , Q ( x, y ) и их частные
производные непрерывны в односвязной области и
¶P ¶Q
=
.
¶y ¶x
13.
du ( x, y ) = P ( x, y ) dx + Q ( x, y ) dy ,du ( x, y ) = 0, u ( x, y ) = C ,
u=
x
y
x0
y0
ò P ( x, y ) dx + ò Q ( x0 , y ) dy = C.
14. Примеры. 1)
() (
Примеры. 1)
¶P
¶Q
= 1 + cos y,
= 1 + cos y.
¶x
¶y
(
)
e x + y + sin y dx + e y + x + x cos y dy = 0.
¶u
= P ( x, y ) ,
¶x
)
u = ò e x + y + sin y dx + C ( y ) = e x + xy + x sin y + C ( y ) .
¶u
= x + x cos y + C ¢ ( y ) = Q ( x, y ) = x + x cos y + e y ,
¶y
C¢ ( y ) = e y , C ( y ) = e y ,
e x + xy + x sin y + e y = C1.
15. 2)
¶Q¶P
= 1,
= 1.
¶y
¶x
x
y
x0
y0
ò P ( x, y ) dx + ò Q ( x0 , y ) dy = C.
x0 = y0 = 0.
Положим
y
x
)
(
y + x dy = 0.
x
+
y
1
dx
+
e
(
)
x
ö
y
y = C,
y dy = C , ç
+
yx
x
+
e
÷
x
+
y
1
dx
+
e
)
ò(
ò
ç 2
÷
0
è
ø
0
0
o
x2
2
+ yx - x + e y - 1 = C ,
æ x2
x2
+ yx - x + e y = C.
2
16. Интегрирующий множитель.
¶P ¶Q¹
,
Если ¶y ¶x то вводят интегрирующий множитель
такой m = m ( x, y ) , что ¶mP = ¶mQ .
¶y
¶x
1) Если m = m ( x ) , то
m=e
2) Если m = m ( y ) , то
m=e
ò
( ¶P / ¶y -¶Q / ¶x ) dx
-ò
Q
.
( ¶P / ¶y -¶Q / ¶x ) dy
P
.
17. Пример.
( x cos y - y sin y ) dy + ( x sin y + y cos y ) dx = 0.¶P
¶Q
= x cos y + cos y - y sin y,
= cos y.
¶y
¶x
æ ¶P ¶Q ö
ç ¶y - ¶x ÷ x cos y - y sin y
è
ø=
= 1,
Q
x cos y - y sin y
( ¶P / ¶y -¶Q / ¶x )
m=e
ò
Q
dx
= e ò dx = e x .
e x ( x cos y - y sin y ) dy + e x ( x sin y + y cos y ) dx = 0.
¶P1
¶Q1
x
= e ( x cos y + cos y - y sin y ) ,
= e x ( x cos y - y sin y ) + e x cos y,
¶y
¶x
¶P1 ¶Q1
=
.
¶y
¶x
18.
e x ( x cos y - y sin y ) dy + e x ( x sin y + y cos y ) dx = 0.¶u
= e x ( x cos y - y sin y ) ,
¶y
u = ò e x ( x cos y - y sin y ) dy + C ( x ) = xe x sin y + ye x cos y - e x sin y + C ( x ) .
¶u
= e x sin y + xe x sin y + e x y cos y - e x sin y + C ¢ ( x ) = e x ( x sin y + y cos y ) ,
¶x
C ¢ ( x ) = 0, C = const.
u = xe x sin y + ye x cos y - e x sin y = C.












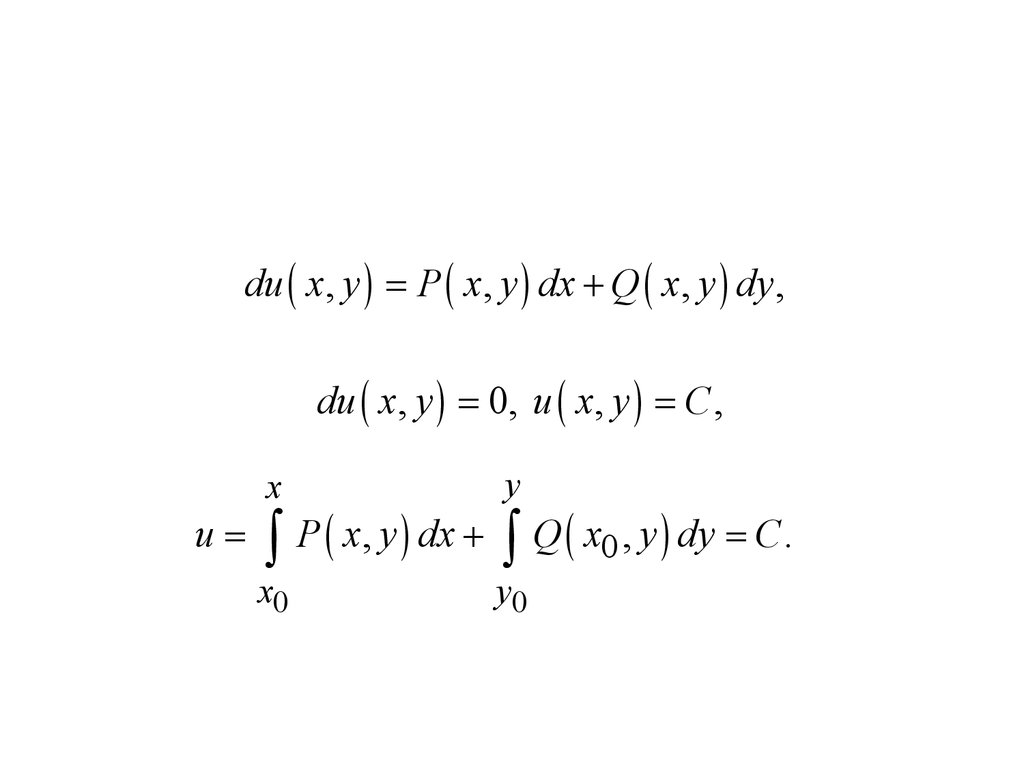





 Математика
Математика








