Похожие презентации:
Тензор магнитной восприимчивости. Закон изменения момента импульса
1. Магнитооптика
История магнитооптикиДаты – события – люди
Магнитооптика на кафедре магнетизма
Даты – события – люди
2. Тензор магнитной восприимчивости
1. Уравнение Ландау-Лифшица безрелаксационного члена.
а. Компоненты тензора магнитной
восприимчивости.
2. Уравнение Ландау-Лифшица с
релаксационным членом.
а. Компоненты тензора магнитной
восприимчивости.
3. Тензор магнитной проницаемости.
3. Закон изменения момента импульса
J – момент импульсаТ – момент силы
dJ
T
dt
Момент импульса единицы объема магнитной среды – спин электронов в
единице объема с учетом поправок на орбитальное движение
M J
M – намагниченность
γ – гиромагнитное отношение (γ>0)
1 dM
T
dt
Вращающий момент обусловлен эффективным полем Нэфф
T M H эфф
4. Уравнение Ландау-Лифшица без релаксационного члена
dMH эфф M
dt
F
H эфф
M
F Fобм Fан Fм.у. Fм.ст FН
Домножим обе части уравнения на М
dM
M
H эфф M M
dt
Длина вектора М
dM
dt
2
0
сохраняется со временем
Проекция вектора М на направление Нэфф
сохраняется со временем
Намагниченность прецессирует вокруг направления Нэфф
5. Схема, иллюстрирующая прецессию намагниченности.
6. Из уравнения Ландау-Лифшица получим компоненты тензора магнитной восприимчивости χ
dMH эфф M
dt
M – намагниченность
Нэфф – эффективное поле
γ – гиромагнитное отношение
Нэфф = (hx, hy, Ho); hx, hy<<Ho.
7. M=(mx, my, Mz); mx~my, mx,my<<Mz, Mz~Mo
idM
hx
dt
mx
j
k
hy
Ho
my
Mz
dmx
dt M z hy m y H o
dm y
mx H o M z hx
dt
dM z
dt m y hx mx hy
M=(mx, my, Mz);
mx~my,
mx,my<<Mz,
Mz~Mo
Заменим Mz на Mo
m x M o hy m y H o
m y mx H o M o hx
M z m y hx mx hy 0
8. Ищем решение в виде , , учтем, что и .
Ищем решение в виде mx mxo e ,my myo ei t , учтем, что m x i mx
и m y i m y .
i t
i mx M o hy m y H o
i m y mx H o M o hx
9. Обозначим
o H oi mx M o hy m y o
i m y mx o M o hx
mx i m y o M o hy o
mx o m y i M o hx i
mx oi m y o 2 M o hy o
2
mx oi m y i M o hxi
10. Вычитаем
22
my i o hx i M o hy M o o
Домножим уравнения
mx i m y o M o hy i
mx o m y i M o hx o
2
m
i
m y oi M o hy i
x
2
mx o m y oi M o hx o
Складываем
2
2
mx i o hx M o o hy i M o
χ – тензор магнитной
восприимчивости
mx xx
m yx
y
xy hx
yy hy
11. Поскольку , , , , то с учетом того, что и .
Посколькуmx
xx
hx
,
mx
xy
hy
то с учетом того, что
,
o
Ho
o
yx
и
M o o
my
hx
,
yy
Mo
o
Ho
M o o
o o
yy
2
2
2
2
(i ) o o
hy
.
M o o
Ho
o o
xx
2
2
2
2
2
2
(i ) o
o
o
2
my
2
,
12. Диагональные компоненты тензора χ (действительны и равны)
o oxx yy 2
2
o
2
13. Поскольку ,
Посколькуo
Ho
,
i M o
i M o
xy
2
2
2
2
(i ) o
o
i M o
i M o
yx
2
2
2
(i ) o
o 2
xy yx
14. Недиагональные компоненты тензора χ (мнимые и асимметричные)
xy yxi M o
xy 2
2
o
Тензор χ - эрмитовый
15. Уравнение Ландау-Лифшица
dMH эфф M
dt
F
H эфф
M
Без релаксационного члена
F Fобм Fан Fм.у. Fм.ст FН
С релаксационным членом в форме Гильберта
M
R
M
M o
t
dM
dM
H эфф M
M
dt
M o
dt
С релаксационным членом в форме Ландау
dM
H
эфф M M
H эфф M H эфф
2
dt
M
o
16. Уравнение Ландау-Лифшица с релаксационным членом
dМH
эфф М М
H эфф М H эфф
2
dt
М
o
M – намагниченность
1
Mo
Нэфф – эффективное поле
γ – гиромагнитное отношение
M= (mx, my, Mz); mx ~ my, mx, my <<Mz, Mz ~Mo
Нэфф = (hx, hy, Ho); hx, hy<<Ho,
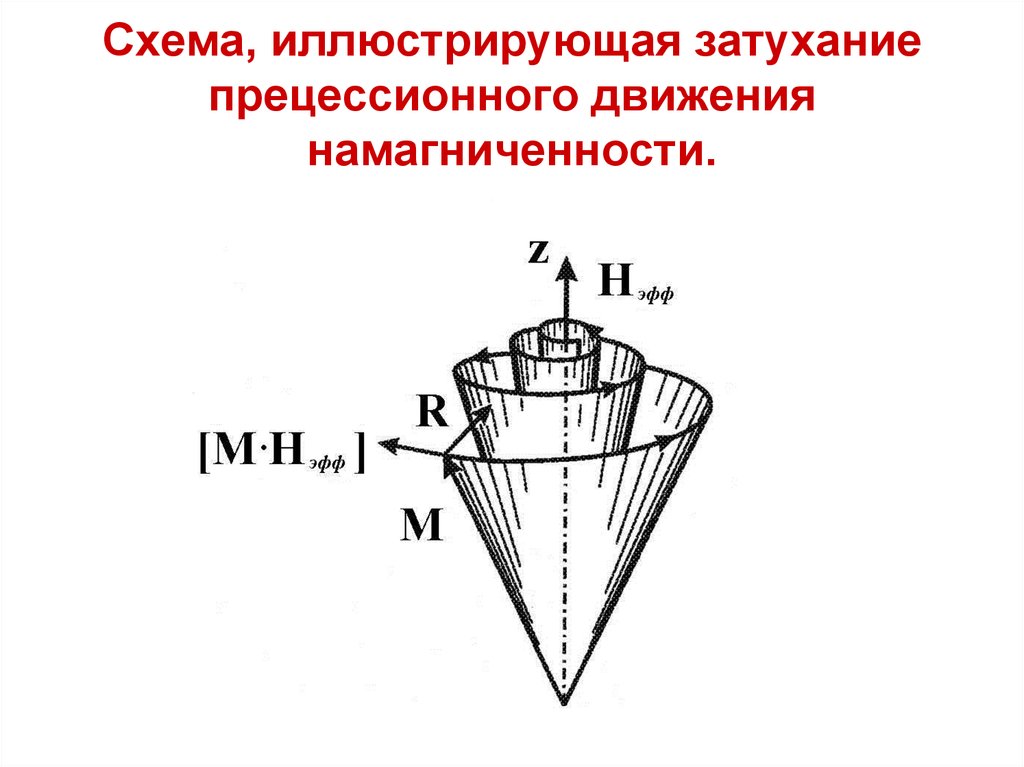
17. Схема, иллюстрирующая затухание прецессионного движения намагниченности.
18. Получим компоненты тензора χ
idM
hx
dt
mx
j
hy
my
k
H эфф M M
H o H эфф
2
M
o
Mz
dmx
mx
hx mx hy m y H o M z
M z hy m y H o hx
2
Mo
dt
my
dm y
hx mx hy m y H o M z
mx H o M z hx hy
2
Mo
dt
dM z m h m h H M z h m h m H M
y
x
x
y
y y
o
z
o М 2 x x
dt
o
19. Заменим Mz на Mo
00
mx
m x M o hy my H o hx
2 hx mx hy m y H o M o
Mo
0
0
m
m y mx H o M o hx hy y2 hx mx hy my H o M o
M
o
0
0
0
0
M m h m h H M o h m h m H M
y
x
x
y
y
y
o
o
o M 2 x x
z
o
M oHoM o
0
H o
2
Mo
20. Ищем решение в виде , , учтем, что и . От коэффициентов при ε оставим только слагаемые, дающие наибольший вклад.
mx mxoei t , my myo ei t ,m y i my . От
Ищем решение в виде
учтем, что m x i mx и
коэффициентов при ε оставим только
слагаемые, дающие наибольший вклад.
mx H o M o
i mx M o hy my H o hx
2
Mo
mx H o
M o hy my H o hx
Mo
i m m H M h h my H o M o
2
y
x
o
o x
y
M
o
my H o
mx H o M o hx hy M
o
21. Обозначим ,
Обозначимo H o
,
H o
Mo
i mx M o hy my o hx mx
i my mx o M o hx hy my
mx i m y o hx M o hy o
mx o m y i M o hx hy i
2
mx o i my o hx o M o hy o
2
mx o i my i M o hx i hy i
Вычитаем
my i o hx o i M o M o hy M o o i
2
2
22. Домножим уравнения
mx i m y o hx M o hy imx o m y i M o hx hy o
2
mx i my o i hx i M o hy i
2
mx o my o i M o hx o hy o
Складываем
mx i o hx i M o o hy i M o M o o
2
2
23. Поскольку , , , , то с учетом того, что , , , .
mxmx
my
my
Поскольку xx
, xy , yx , yy
,
hy
hx
hx
hy
то с учетом того, что
M o o 2 2 , o 2
,
.
o
Ho
,
Mo
o
Ho
o
,
Ho M o
M o o i
M o o i H o
M o Ho
xx
2
2
2
2
(i ) o
o 2i
0
o o 2 i o
o 2 i
2
o 2
2
o 2i
o 2 2i
24.
oHo M o
M o o i
M o o i H o
M o Ho
yy
2
2
2
2
(i ) o
o 2i
0
o o 2 i o
o 2 i
2
o 2
2
o 2i
o 2 2i
xx yy
Диагональные компоненты тензора χ равны
25. Недиагональные компоненты тензора χ
oxy
Mo
H o
o i M o
M o o i M o H o
Mo
2
(i ) 2 o
o 2 2 2i
i M o
o 2 2 2i
o M o i M o
yx
2
2
(i ) o
o
o
Ho
Mo
H o
i M o
Mo
o 2 2 2i
i M o
2
o 2 2i
xy yx i a
Тензор χ - эрмитовый
26.
• Компоненты тензора восприимчивости –комплексные, т.к. среда поглощает энергию
магнитного поля. Диссипация энергии
связана с мнимыми частями χ и χа.
• Получим действительные и мнимые части
χ и χа. Учтем, что ' i " и a a ' i a " .
27. Диагональные компоненты
' o" o
o 2 o 2 2 2 2 2
H o
Mo
2
o 2
2 2
2
o
2
o
4
2 2
2
2
4
2
действительная
мнимая
2
28. Недиагональные компоненты
M o oa ' 2
2
2
2
2
o 4
2
2
a "
o
2 M o
2
2
2
4
2
2
мнимая
действительная
2
29. Построим кривую χа”(ω). Упростим выражение χа”(ω).
2 M o2 M o
a " 4
4
2
2
4
2
4
2
2
o 2 o 4 2 2 o 2 2 o
2
2
Обозначим ω2=x , тогда
a " ( ) a " ( x)
Пусть A 2 M o , B 2 o 2
Тогда
Ax
a " ( x) 2
x Bx C
2
2
, C o
4
30. Продифференцируем эту функцию
a " 'A x 2 Bx C Ax 2 x B
x
A x Bx C 2 x Bx
A x C
x Bx C
x Bx C
2
2
Bx C
2
2
2
2
2
2
2
Знак производной определяется знаком выражения
x
2
C
31. Поскольку , , точка максимума
Поскольку x C , x 0точка максимума o
,
C
х
a " ( x)
a " ' ( x)
─
0
C
max
0
+
─
Сделаем обратную замену и определим значение функции χa″
в точке максимума
2 M o o M o
a " 2
2
2
2
2
2
2
2
4 o
o 4
2 M o
2
2
Увеличение δ приводит к уширению функции
и уменьшению ее максимального значения.
Аналогичные исследования можно провести для χa′(ω)
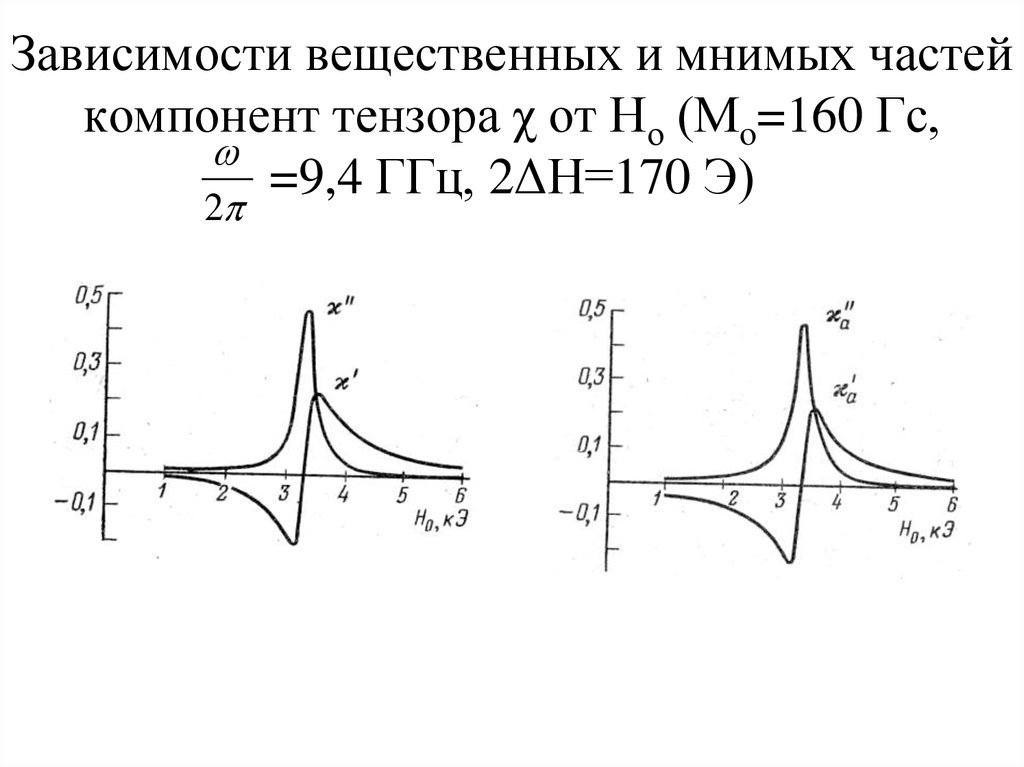
32. Зависимости вещественных и мнимых частей компонент тензора χ от Но (Мo=160 Гс, =9,4 ГГц, 2ΔН=170 Э)
233. Тензор магнитной проницаемости
ik 4o M o
1 4 2
2
o
i M o
4 2 2
o
0
i M o
4 2
2
o
o M o
1 4 2
o 2
0
0
0
1
34.
22
Оценки: 10 10 Гц, o 10 Гц,
o
o М o
7
4 2
10
2
.
o
13
14
10
М o
3
4 2
10
2
o
Это обеспечивает вращение плоскости
поляризации на 60 – 80 о/см.
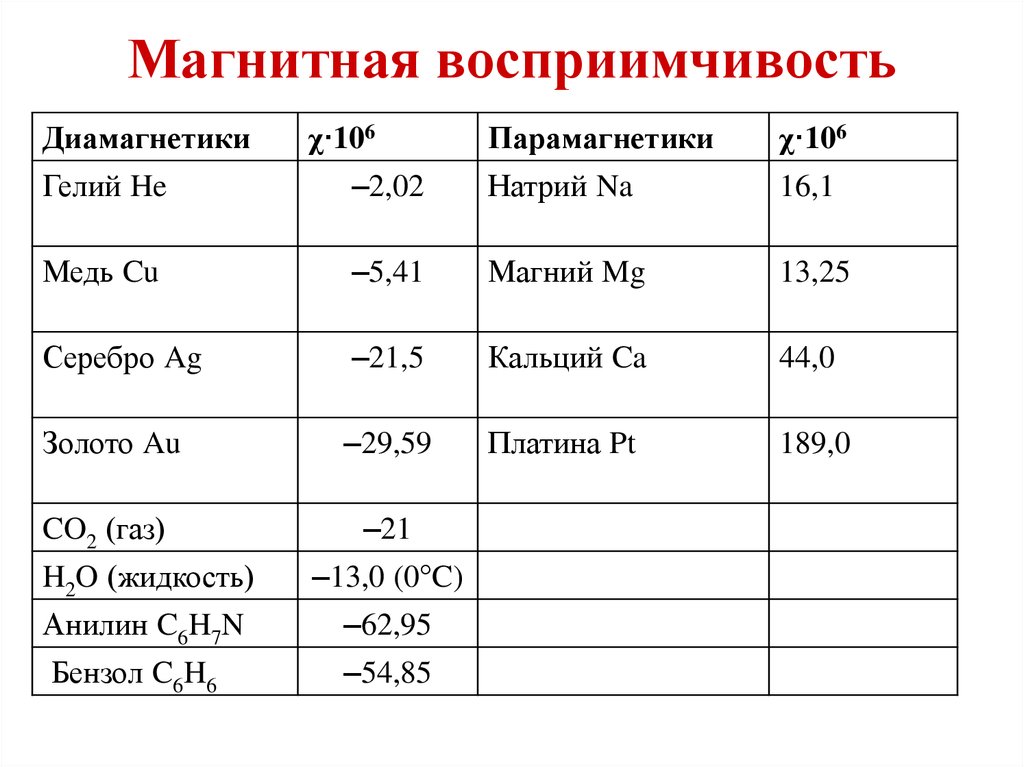
35. Магнитная восприимчивость
Диамагнетикиχ·106
Парамагнетики
χ·106
Гелий He
–2,02
Натрий Na
16,1
Медь Cu
–5,41
Магний Mg
13,25
Серебро Ag
–21,5
Кальций Ca
44,0
Золото Au
–29,59
Платина Pt
189,0
CO2 (газ)
–21
H2O (жидкость)
–13,0 (0°C)
Анилин C6H7N
–62,95
Бензол C6H6
–54,85
36.
• Используя уравнение ЛандауЛифшица, были полученыкомпоненты тензоров χ и μ
• Эти тензоры являются эрмитовыми
• Спин-орбитальное взаимодействие
– причина того, что μxy = –μyx
37. Тензор магнитной восприимчивости
1. Уравнение Ландау-Лифшица безрелаксационного члена.
а. Компоненты тензора магнитной
восприимчивости.
2. Уравнение Ландау-Лифшица с
релаксационным членом.
а. Компоненты тензора магнитной
восприимчивости.
3. Тензор магнитной проницаемости.






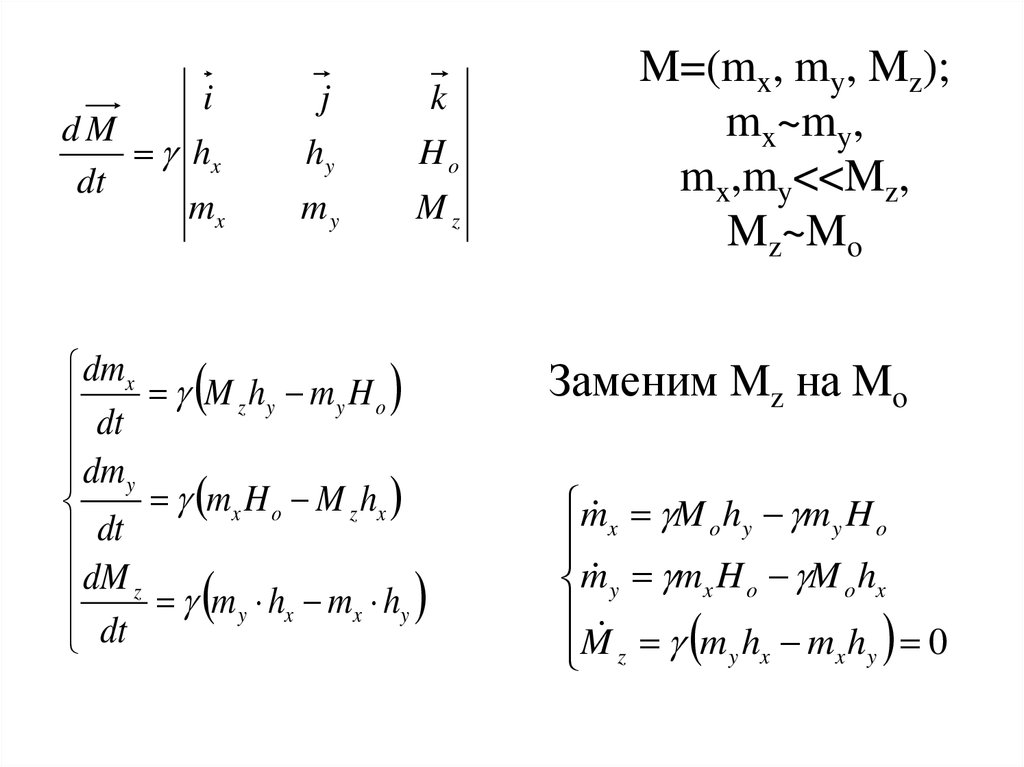

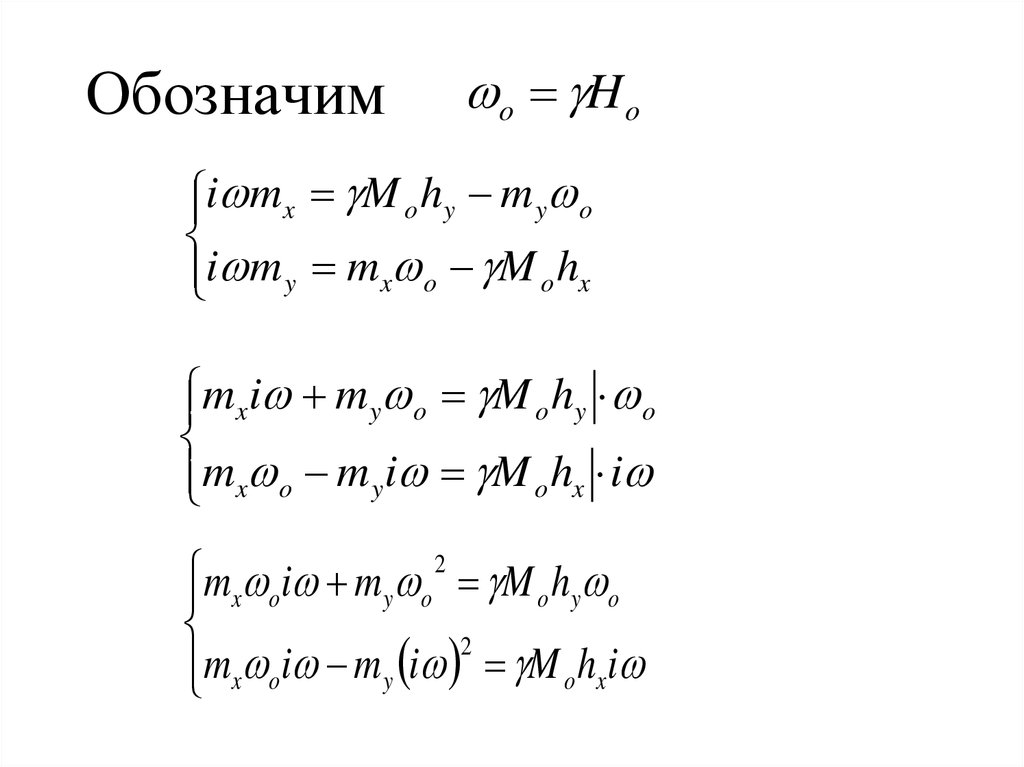










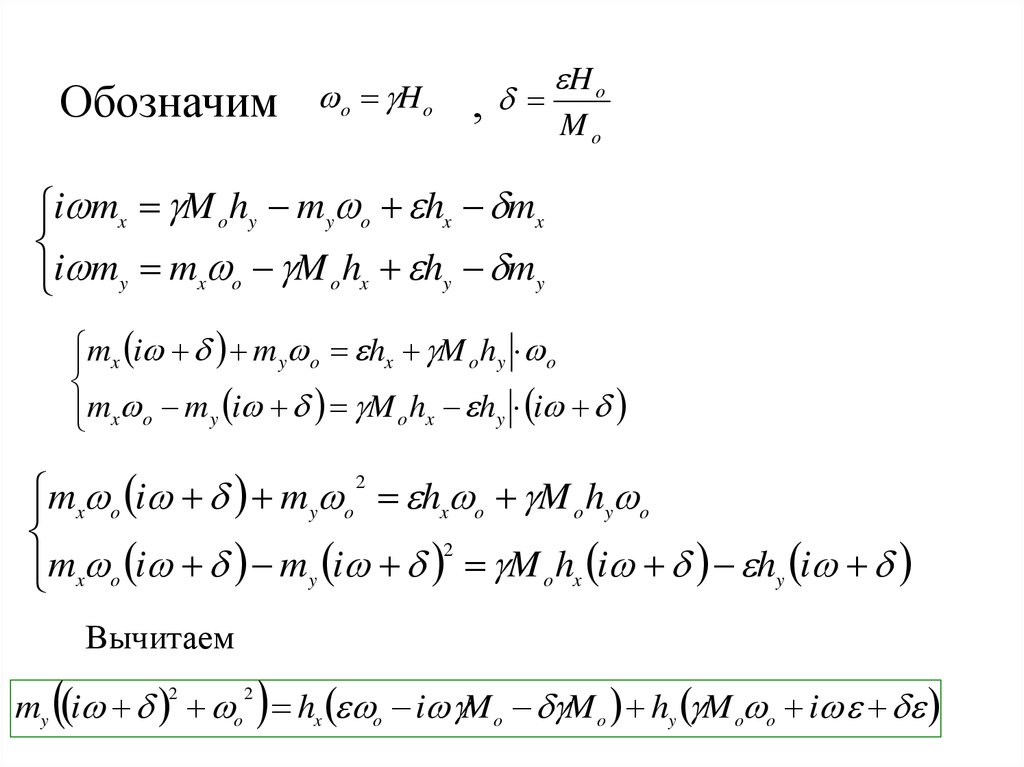














 Физика
Физика








