Кинематика вращательного движения

1.

Кинематика вращательного движения

2.

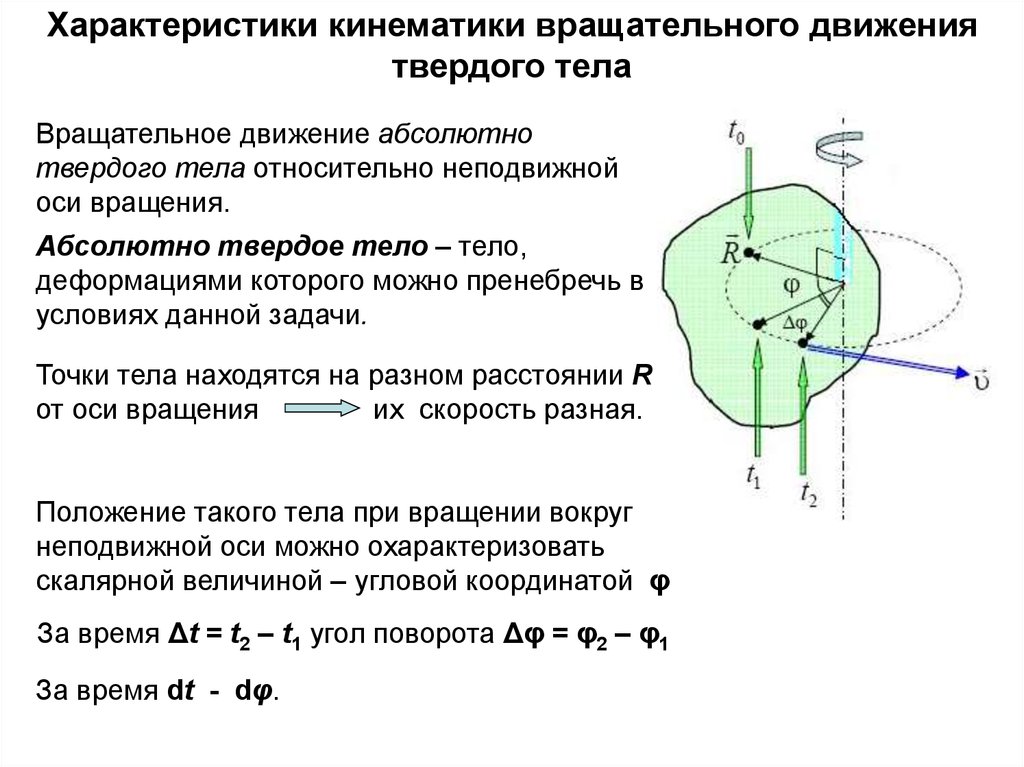
Характеристики кинематики вращательного движения
твердого тела
Вращательное движение абсолютно
твердого тела относительно неподвижной
оси вращения.
Абсолютно твердое тело – тело,
деформациями которого можно пренебречь в
условиях данной задачи.
Точки тела находятся на разном расстоянии R
от оси вращения
их скорость разная.
Положение такого тела при вращении вокруг
неподвижной оси можно охарактеризовать
скалярной величиной – угловой координатой φ
За время Δt = t2 – t1 угол поворота Δφ = φ2 – φ1
За время dt - dφ.

3.

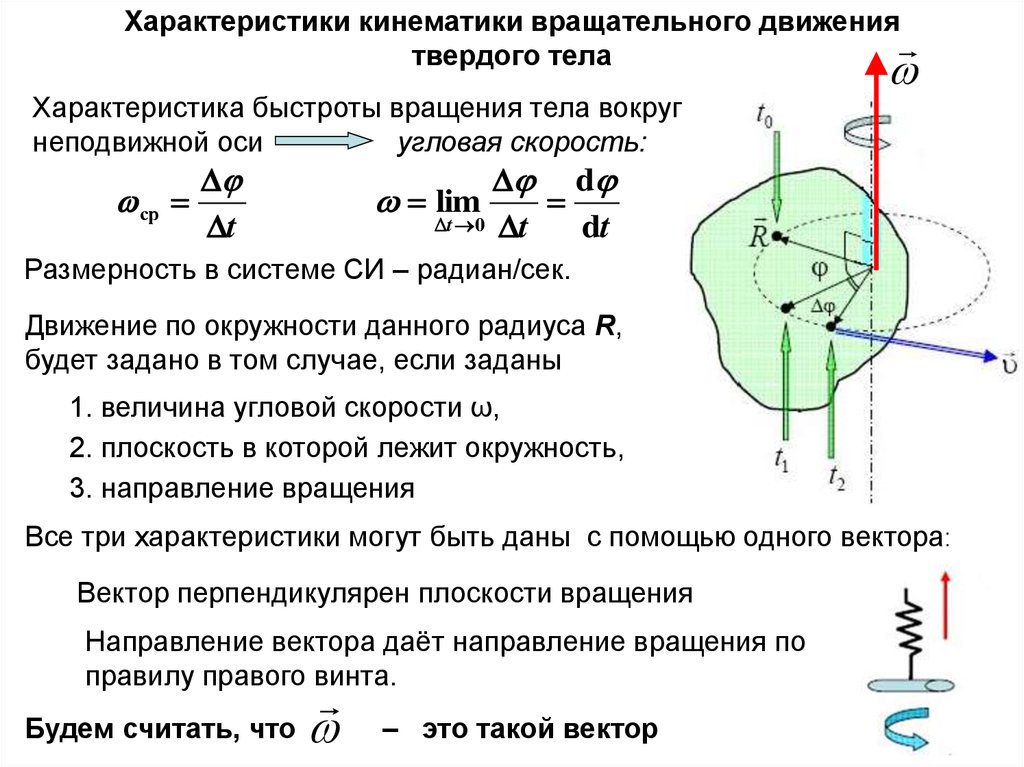
Характеристики кинематики вращательного движения
твердого тела
Характеристика быстроты вращения тела вокруг
неподвижной оси
угловая скорость:
d
lim
t 0 t
dt
ср
t
Размерность в системе СИ – радиан/сек.
Движение по окружности данного радиуса R,
будет задано в том случае, если заданы
1. величина угловой скорости ω,
2. плоскость в которой лежит окружность,
3. направление вращения
Все три характеристики могут быть даны с помощью одного вектора:
Вектор перпендикулярен плоскости вращения
Направление вектора даёт направление вращения по
правилу правого винта.
Будем считать, что
– это такой вектор

4.

Характеристики кинематики вращательного движения
твердого тела
Т – период обращения
T
2
2
T
- частота вращения: величина обратная периоду – число оборотов в
единицу времени:
1
2
T 2
и можно рассматривать и как характеристики движения с
Т
переменной угловой скоростью. Тогда они будут характеризовать
вращение в данный момент времени.

5.

Характеристики кинематики вращательного движения
твердого тела
Угловое ускорение - характеристика
быстроты изменения угловой скорости
d
dt
При неподвижной оси вращения и
совпадают по направлению в случае
ускоренного вращательного движения.
В случае замедленного
вращательного
движения и - противоположны.

6.

Связь угловых и линейных величин
Путь, пройденный точкой при движении по окружности:
S R
Связь между модулями линейной скорости точки тела и угловой
скоростью:
R
dS d( R )
d
R
R
dt
dt
dt
Связь между модулями тангенциального ускорения точки тела
и углового ускорения:
d d( R) R d
R
a
dt
dt
dt
a R
.
Связь между модулем нормального ускорения точки тела и
модулем угловой скорости:
2
an
R
2R

7.

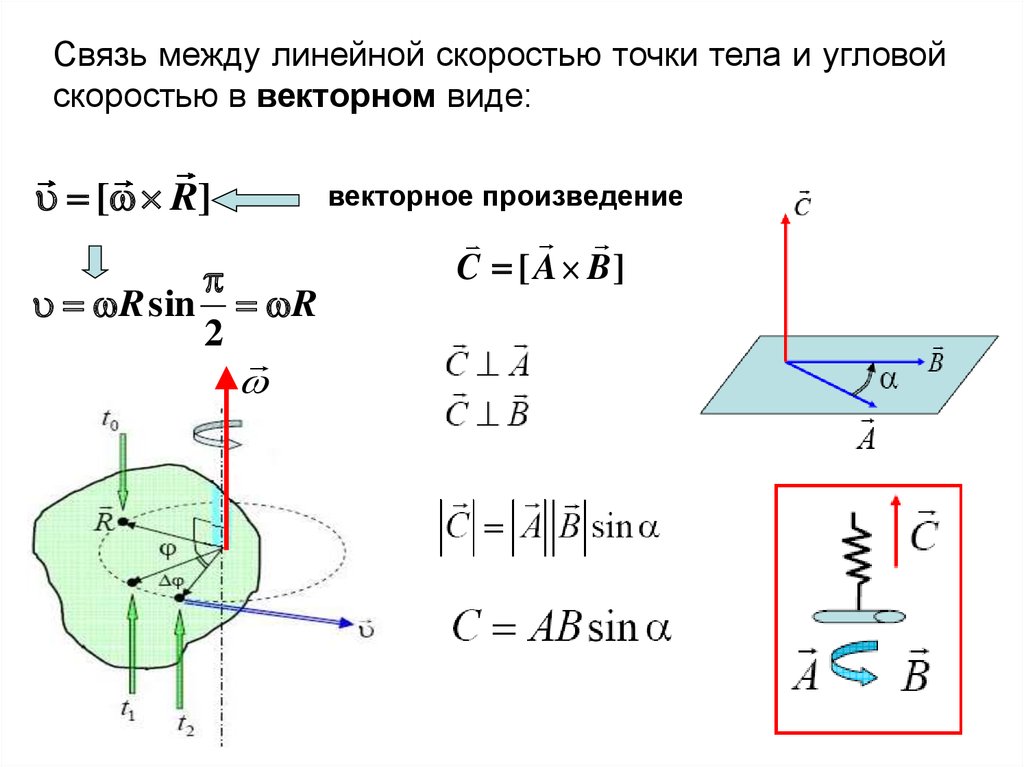
Связь между линейной скоростью точки тела и угловой
скоростью в векторном виде:
[ R]
R sin R
2
.
векторное произведение
C [ A B]

8.

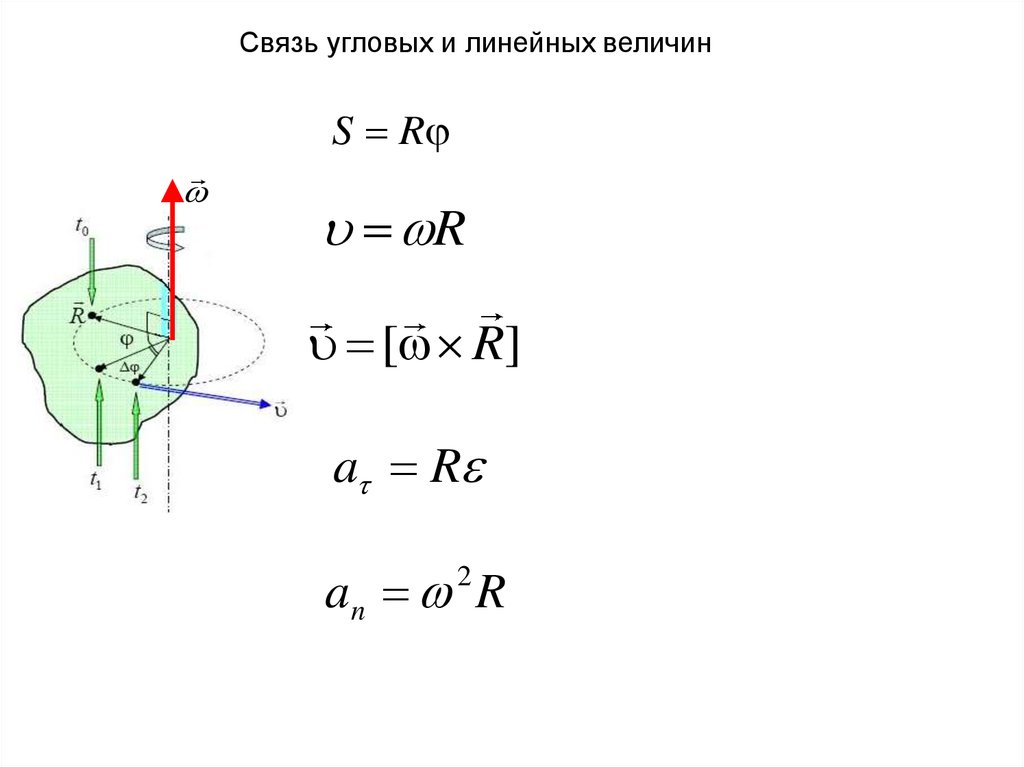
Связь угловых и линейных величин
S R
R
[ R]
a R
an R
2

9.

Поступательное движение
dr
t
dt
d
t
dt
d
dt
d
a
dt
t
r t r t 0 d
t0
Вращательное движение
t
t t 0 a d
t0
t
t t 0 d
t0
t
t t 0 d
t0

10.

Первый закон Ньютона
Инерциальные системы отсчета
Тело движется равномерно и прямолинейно
или сохраняет состояние покоя, пока
воздействие других тел не изменит это
состояние (закон инерции)
“Движущееся тело останавливается, если
сила, его толкающая, прекращает свое
действие” - Аристотель
Эмпирический закон – обобщение большого количества опытных фактов.
Практически силы бывают скомпенсированы.
Пример: на катящийся вагон действует вес и реакция опоры. В
результате, если трение мало, вагон движется почти равномерно.

11.

Первый закон Ньютона
Инерциальные системы отсчета
Тело движется равномерно и прямолинейно
или сохраняет состояние покоя, пока
воздействие других тел не изменит это
состояние (закон инерции)
Инерциальная система
отсчета
система отсчета, в которой
соблюдается первый закон
Ньютона.

12.

Принцип относительности Галилея.
Все инерциальные системы отсчета эквивалентны
друг другу. И никакими механическими опытами,
проведенными в данной инерциальной системе
отсчета, нельзя определить, движется система или
нет.
Примеры. Вагон поезда
Земля – инерциальная система с высокой степенью точности.
Можно ли с помощью какого-либо механического опыта установить, что
Земля всё-таки не вполне инерциальная система?

13.

Маятник Фуко:
демонстрация
неинерциальности системы
отсчета, связанной с Землей.

14.

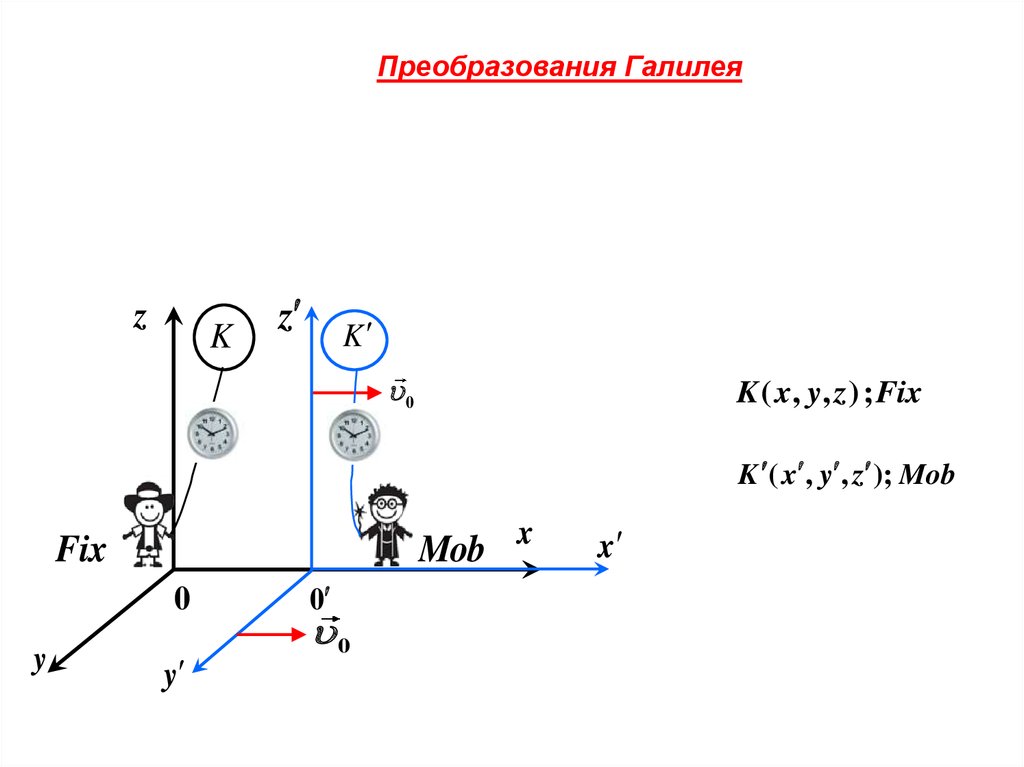
Преобразования Галилея
z
K
z
K
0
K ( x, y, z ) ; Fix
K ( x , y , z ); Mob
Mob x
Fix
0
y
y
0
0
x

15.

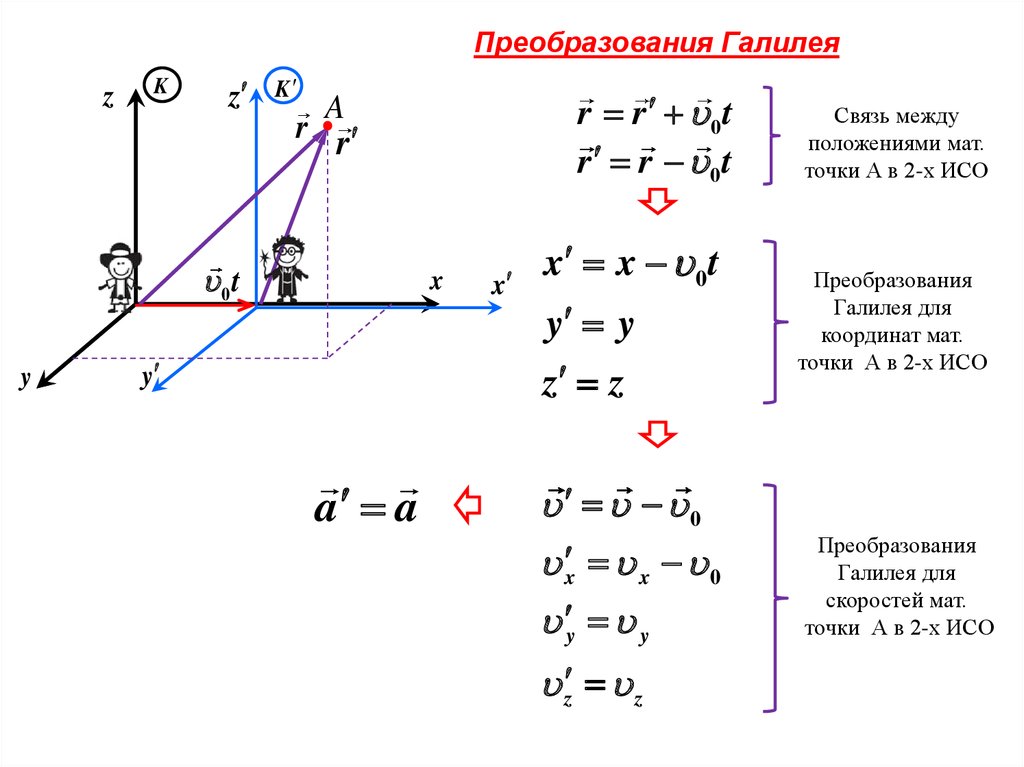
Преобразования Галилея
z
K
z
K
r r 0t
r r 0t
A
r r
0t
y
x
y
a a
x
x x 0 t
y y
z z
0
x x 0
y y
z z
Связь между
положениями мат.
точки А в 2-х ИСО
Преобразования
Галилея для
координат мат.
точки А в 2-х ИСО
Преобразования
Галилея для
скоростей мат.
точки А в 2-х ИСО

16.

Трудности классической механики.
Если измерение скорости света в
данной ИСО позволит определить её
скорость относительно абсолютной
ИСО, то следует подвергнуть
сомнению принцип относительности
Галилея !!!???

17.

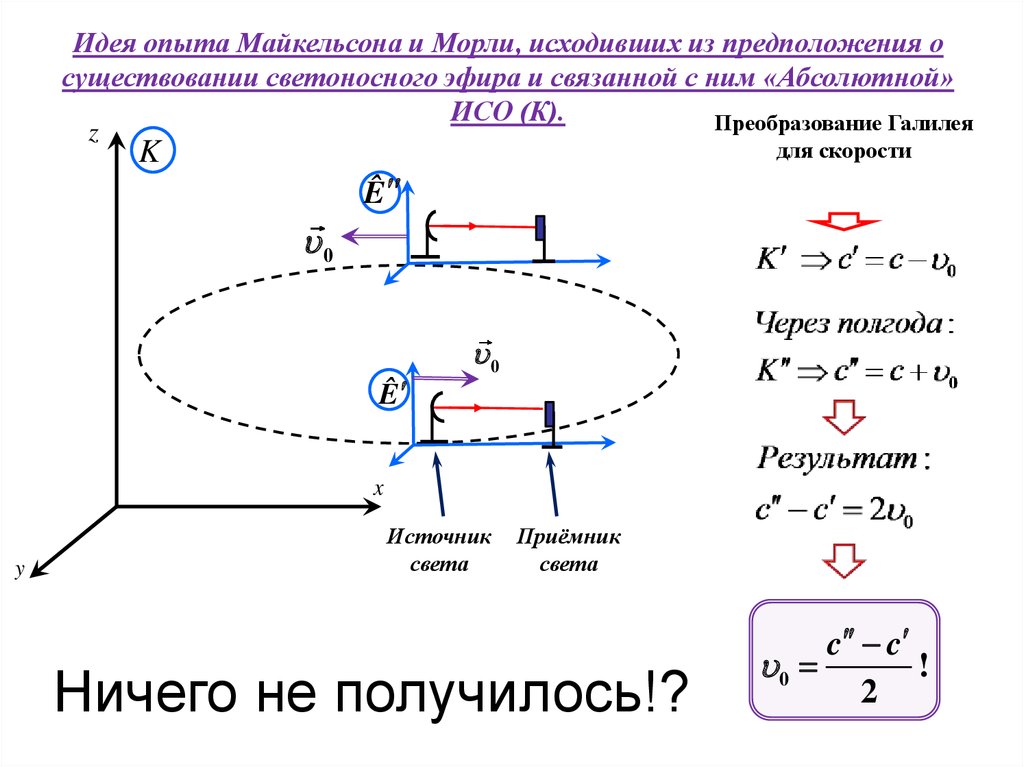
Идея опыта Майкельсона и Морли, исходивших из предположения о
существовании светоносного эфира и связанной с ним «Абсолютной»
ИСО (К).
Преобразование Галилея
z
для скорости
K
Ê
0
Ê
0
x
y
Источник
света
Приёмник
света
Ничего не получилось!?
c c
0
!
2

18.

Скорость света во всех экспериментах была
одинаковой.
Cветоносного эфира нет!
с"=с'=с = 3 108 м/с
Принцип относительности может
применяться также и к оптическим
явлениям!

19.

Постулаты специальной теории относительности А.Эйнштейна
1. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
Все инерциальные системы отсчета(ИСО) эквивалентны
друг другу. Никакими физическими опытами, проведенными в
данной ИСО, нельзя определить, движется система или
нет.
2. ПРИНЦИП ИНВАРИАНТНОСТИ СКОРОСТИ СВЕТА
Скорость света в вакууме не зависит от движения
источника или наблюдателя и одинакова во всех
направлениях, т.е. одинакова во всех системах отсчета.
с = 3 108 м/с

20.

Некоторые выводы Специальной Теории Относительности
Скорость света – предельная скорость.
Относительность одновременности
Замедление времени
t
t 0
1
Сокращение линейных размеров
02
c2

21.

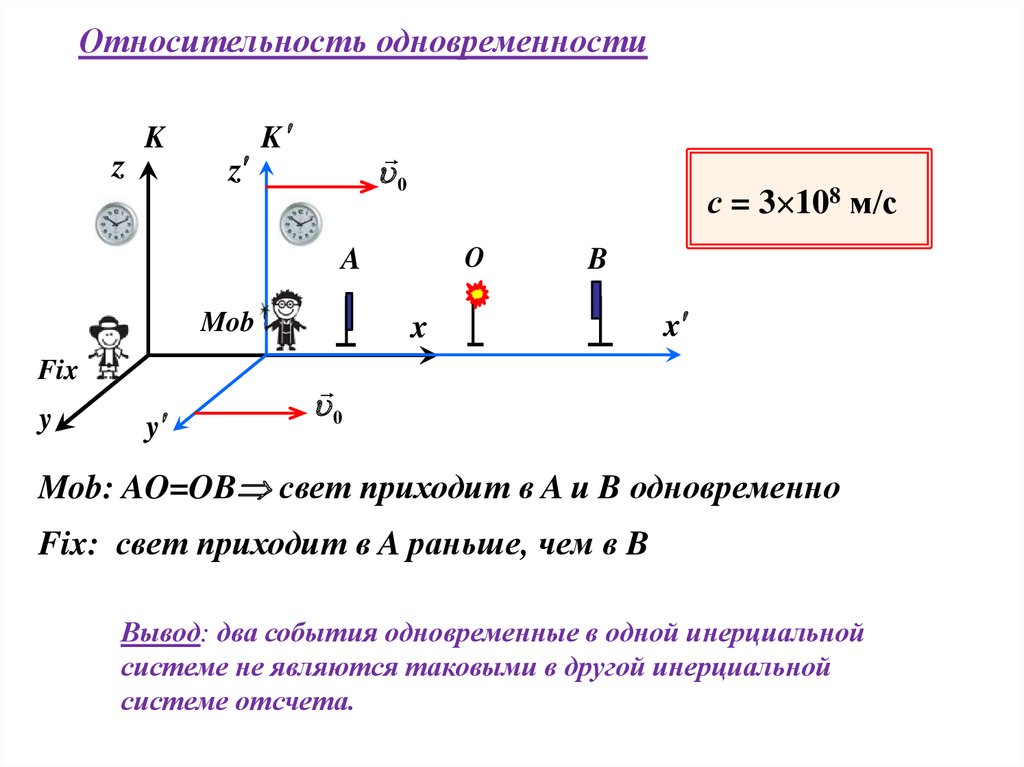
Относительность одновременности
z
K
z
K
0
с = 3 108 м/с
O
A
Mob
Fix
y
B
x
x
y
0
Mob: AO=OB свет приходит в A и B одновременно
Fix: свет приходит в A раньше, чем в B
Вывод: два события одновременные в одной инерциальной
системе не являются таковыми в другой инерциальной
системе отсчета.

22.

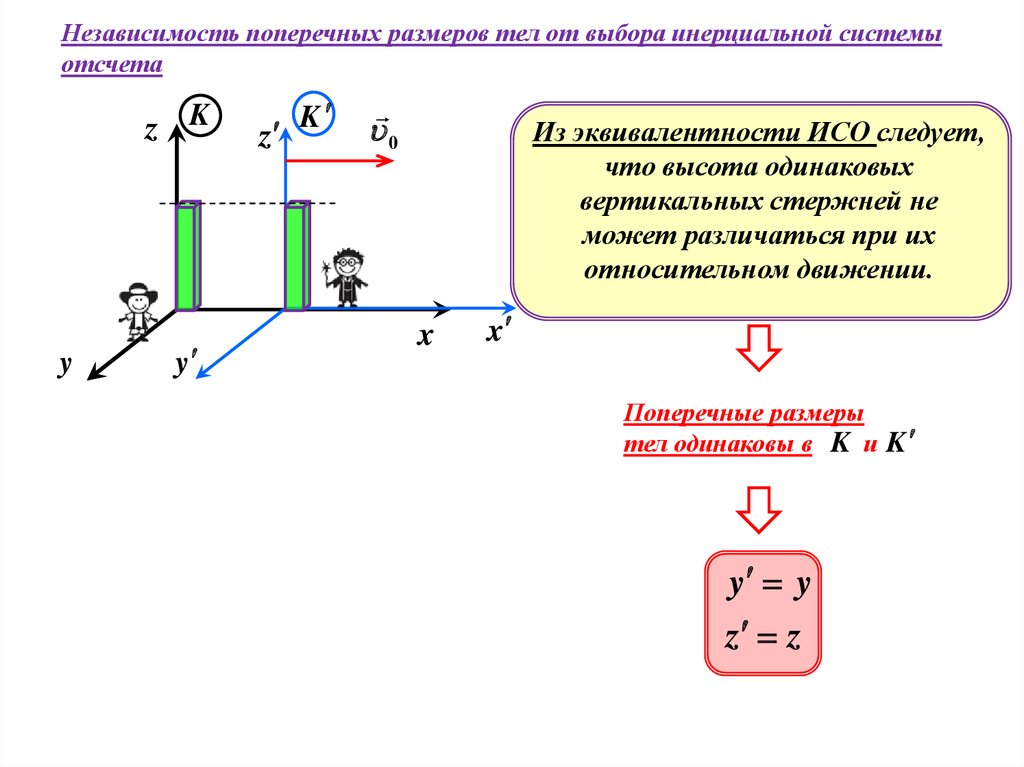
Независимость поперечных размеров тел от выбора инерциальной системы
отсчета
z K
y
y
z
K
0
Из эквивалентности ИСО следует,
что высота одинаковых
вертикальных стержней не
может различаться при их
относительном движении.
x
x
Поперечные размеры
тел одинаковы в K и K
y y
z z

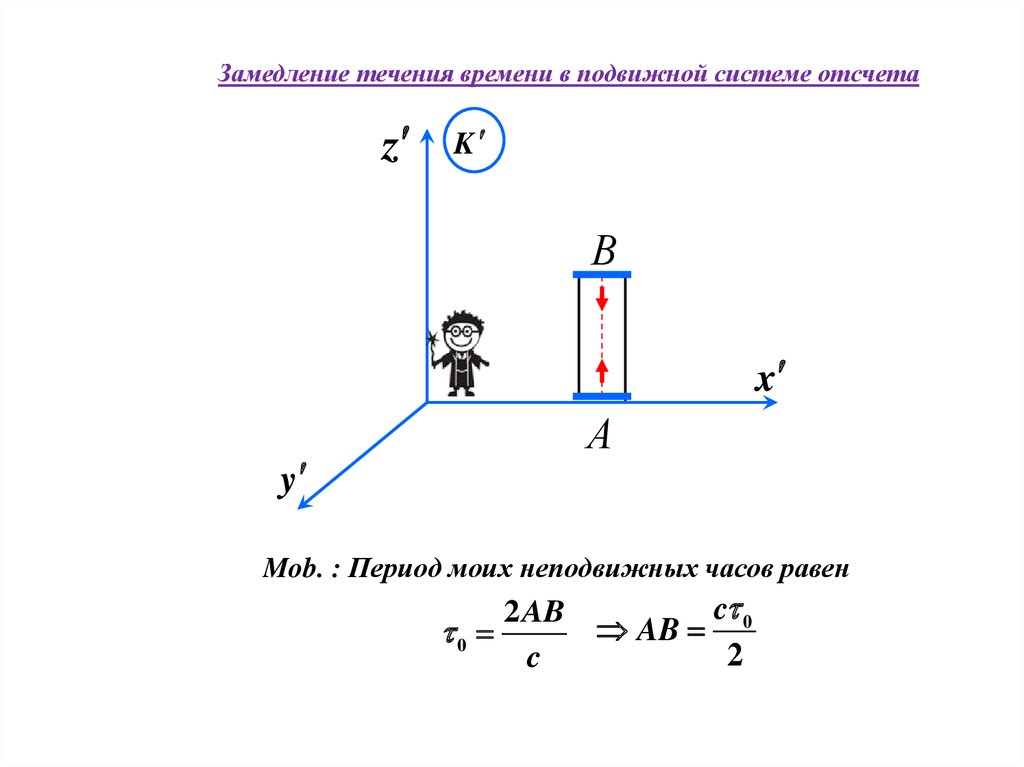
23.

Замедление течения времени в подвижной системе отсчета
z
K
В
x
y
А
Mob. : Период моих неподвижных часов равен
c 0
2AB
AB
0
2
c

24.

z K
c
2
0
B
0
A
Fix: Mob, твои часы двигаются
со скоростью 0 :
c 0
2
2
2
2
2
2 0
c 0
c 0
AB
2 2
2 2
AB
0
2
x
2
2
2 2
2
c 0 c 0 2 c 0
2
2
c
2
2
2
0
y
Период подвижных часов:
0
1
0
t
2
c2
t 0
1
02
Вывод: Время в подвижной системе отсчета течет медленнее, чем в
покоящейся системе отсчета.
t0 t
Собственное время (минимально)
c2

25.

Экспериментальное доказательство:
нестабильные частицы мюоны с
временем жизни 2 мкс. (собственное
время), образующиеся в верхних слоях
атмосферы (20-30 км) достигают
поверхности Земли.
С точки зрения классической физики
макс. расстояние, пролетаемое мюонами,
не должно быть более 2 10 6 3 108 600 м.
С т. з. наблюдателя на земле: их время течет медленнее.
С т. з. мюонов: расстояние до земли сокращается.

26.

Преобразования Лоренца
x , y , z , t x , y , z , t
Преобразования Лоренца - результат поиска соотношений,
оставляющих инвариантными (неизменными) законы физики.
x
0
c
x 0t
1 2
y y
z z
t 0 2 x
c
t
1 2
x x 0 t
y y
z z
t t
Когда 0 c ( 0), преобразования Лоренца переходят в
преобразования Галилея.

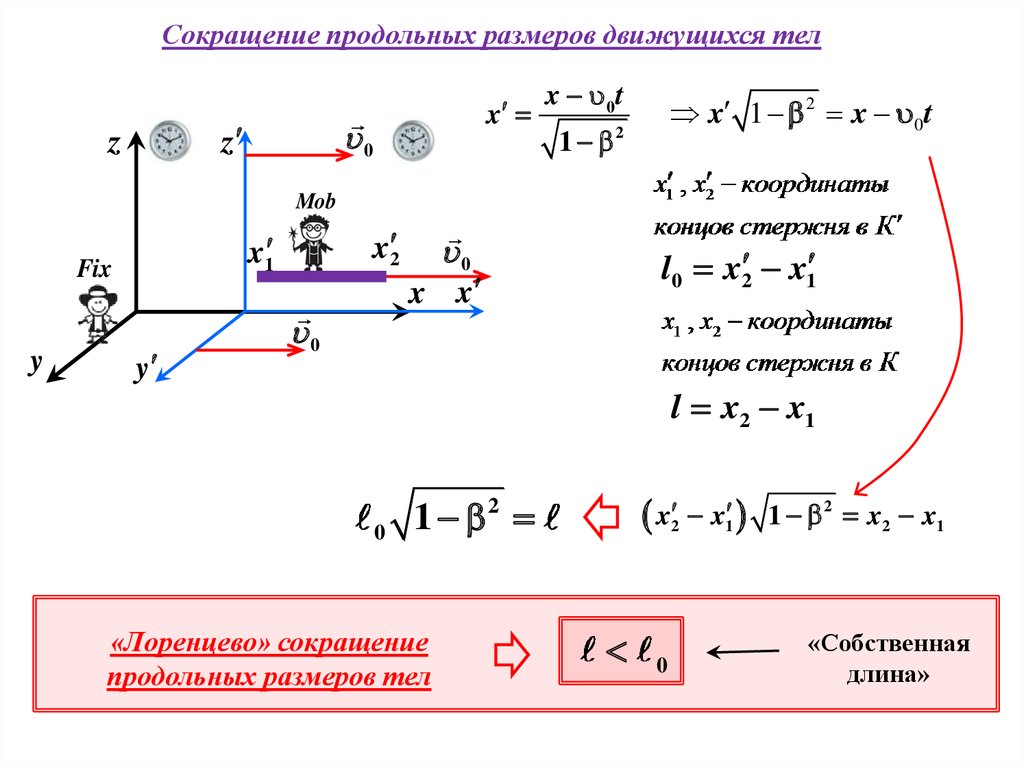
27.

Сокращение продольных размеров движущихся тел
0
z
z
x
x 0t
x 1 2 x 0 t
1 2
Mob
x 2
x1
Fix
y
y
0
0
x x
l0 x 2 x1
l x2 x1
x2 x1
1
2
0
«Лоренцево» сокращение
продольных размеров тел
0
1 2 x2 x1
«Собственная
длина»

28.

Изменение формы тел, движущихся со скоростью близкой к скорости света,
из-за сокращения их продольных размеров

29.

Взаимодействие тел. Второй закон Ньютона.
F
Второй закон Ньютона связывает силу, массу и ускорение. a
m
Сила даёт меру и направление воздействия, оказываемого на данное тело
со стороны других тел.
Масса отвечает за то как тело «отзывается» на данное воздействие , т.е.
за его инертность.
Сила вызывает
изменение скорости тела и его деформацию.
Пример: сила вызывает деформацию пружины и эта
деформация пропорциональна приложенной силе.
Прибор для измерения силы – динамометр.
Силу можно измерить и благодаря этому сравнивать силы
разной природы, например, гравитационные,
электромагнитные и др.

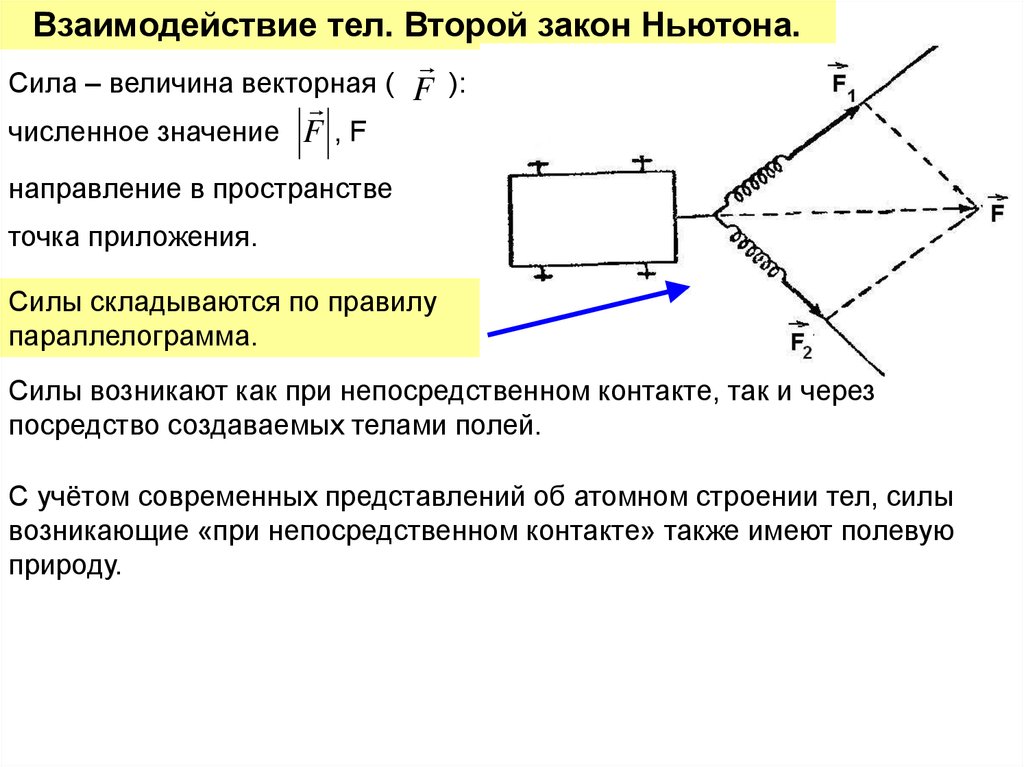
30.

Взаимодействие тел. Второй закон Ньютона.
Сила – величина векторная ( F ):
численное значение F , F
направление в пространстве
точка приложения.
Cилы складываются по правилу
параллелограмма.
Силы возникают как при непосредственном контакте, так и через
посредство создаваемых телами полей.
С учётом современных представлений об атомном строении тел, силы
возникающие «при непосредственном контакте» также имеют полевую
природу.

31.

Взаимодействие тел. Второй закон Ньютона.
Силы бывают:
1. Гравитационные, действуют на любые массы и
порождаются массой, действуя на расстоянии.
2. Электромагнитные, действуют на заряды и
токи со стороны других зарядов и токов.
3. Ядерные, именно они скрепляют ядро, несмотря на
сильное электростатическое отталкивание между протонами.
4. Слабые силы, имеющие малый радиус
действия (физика элементарных частиц).

32.

Взаимодействие тел. Второй закон Ньютона.
Масса – определяет инерциальные и гравитационные свойства материи.
Современные физические представления
количество материи.
Масса – это просто
Тела состоят из атомов, которые в свою очередь состоят из протонов,
нейтронов и электронов.
m ~ (число протонов + число нейтронов + число электронов)
Чем больше в теле материи (протонов и нейтронов), тем оно сильнее
притягивает другие тела в соответствии с законом всемирного тяготения
m1m2
F
R2
Чем больше в теле материи (протонов и нейтронов), тем труднее изменить
его скорость в соответствии со вторым законом Ньютона:
dv F
a
dt
m
Ускорение, с которым движется материальная точка,
равно отношению результирующей всех сил,
действующих на нее, к ее массе.

33.

Взаимодействие тел. Второй закон Ньютона.
Ускорение, с которым движется материальная точка,
dv F
равно отношению результирующей всех сил,
a
действующих на нее, к ее массе.
dt
m
Важное замечание о гравитационных и инерционных проявлениях массы:
Ускорение свободного падения не зависит от массы (Галилей,
Пизанская башня)
сила притяжения пропорциональна той же массе,
которая стоит во втором законе Ньютона и отвечает за инертность:
с ростом массы растёт сила, но также растёт и инертность – в результате
ускорение остаётся тем же.

34.

Взаимодействие тел. Второй закон Ньютона.
Ускорение, с которым движется материальная точка,
dv F
равно отношению результирующей всех сил,
a
действующих на нее, к ее массе.
dt
m
Второй закон относится к движению материальной точки.
Однако реально он может применяться гораздо шире благодаря теореме о
движении центра масс механической системы:
центр масс движется как точка, масса которой равна массе всей системы,
к которой приложены все внешние силы.
Выбирая в качестве материальной точки центр масс, можно второй закон
применить к любому телу или системе тел.

35.

Взаимодействие тел. Второй закон Ньютона.
Ускорение, с которым движется материальная точка,
dv F
равно отношению результирующей всех сил,
a
действующих на нее, к ее массе.
dt
m
Другая форма записи второго закона Ньютона
d (mv )
F
dt
Вводя импульс материальной точки
p mv
приходим ко второму закону Ньютона в форме
dp
F
dt
Скорость изменения импульса материальной точки во времени равна
результирующей силе, действующей на материальную точку.
Второй закон Ньютона в таком виде справедлив в частности тогда, когда
классическая физика уже не корректна – при скоростях сравнимых со
скоростью света, когда масса зависит от скорости.

36.

Взаимодействие тел. Второй закон Ньютона.
2
d r dv F
a
2
dt
dt
m
Второй закон
описание механических движений с помощью
дифференциалных уравнений
положение тела и его скорость в
любые моменты времени.
Единицы измерения
Основные механические величины в системе СИ:
длина L, м,
масса M, кг,
время Т, сек.
Все другие механические величины производятся из М, L и T с помощью
соответствующих уравнений.
формула размерности
Например, v=ΔS/Δt
F=ma → [F]=MLT-2
→
[v]=LT-1, а= Δv/Δt → [a]=LT-2 ,
кг м/сек2
Ньютон
Размерности в левой и правой части уравнения - одинаковые!!

37.

Третий закон Ньютона,
закон изменения и сохранения импульса системы
материальных точек.
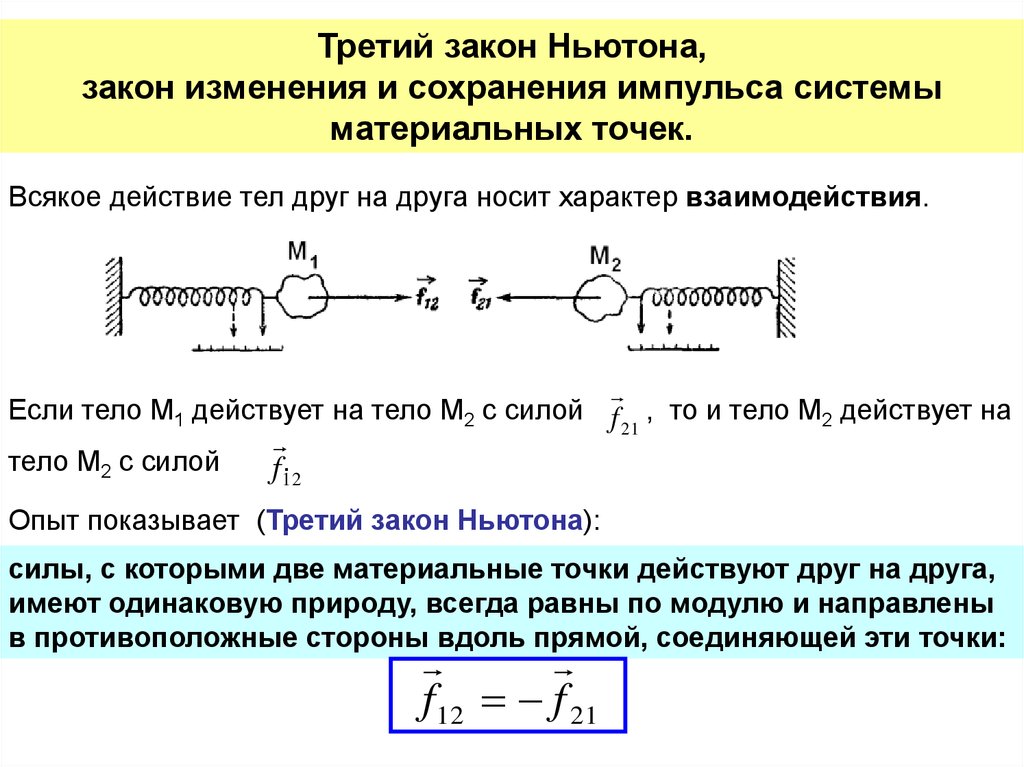
Всякое действие тел друг на друга носит характер взаимодействия.
Если тело М1 действует на тело М2 с силой f , то и тело М2 действует на
21
тело М2 с силой
.
f12
Опыт показывает (Третий закон Ньютона):
силы, с которыми две материальные точки действуют друг на друга,
имеют одинаковую природу, всегда равны по модулю и направлены
в противоположные стороны вдоль прямой, соединяющей эти точки:
f 12 f 21

38.

Третий закон Ньютона,
закон изменения и сохранения импульса системы
материальных точек.
f 12 f 21
Силы всегда возникают попарно.
Эти силы не уравновешивают друг друга - они приложены к разным телам.

39.

Третий закон Ньютона,
закон изменения и сохранения импульса
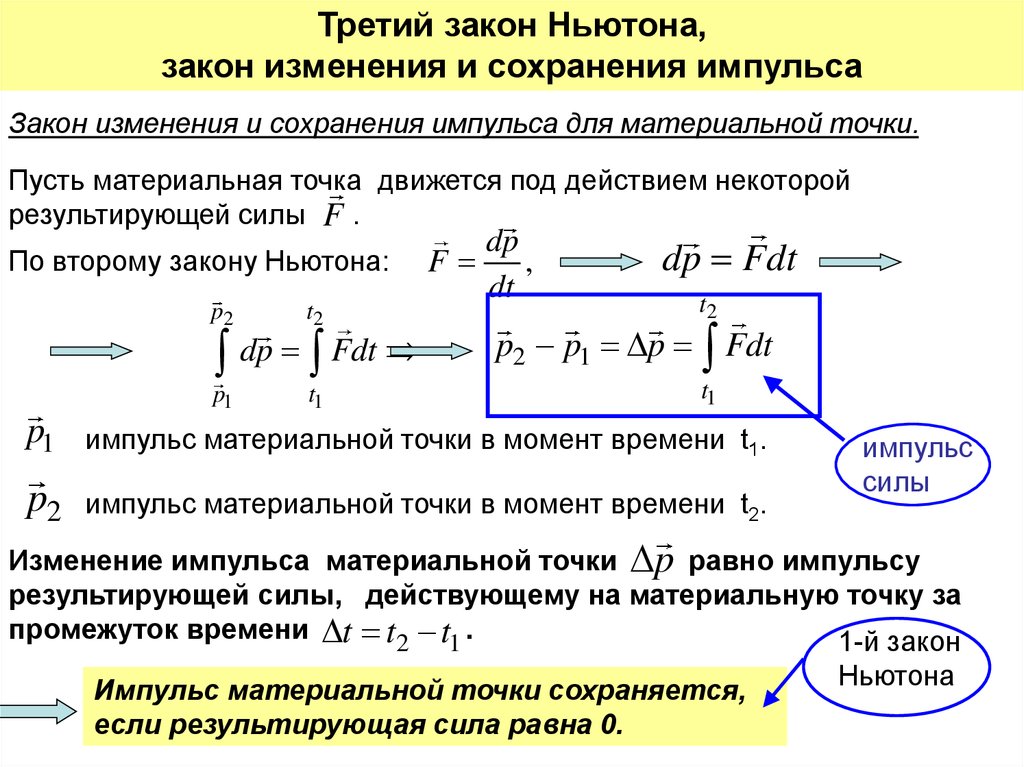
Закон изменения и сохранения импульса для материальной точки.
Пусть материальная точка движется под действием некоторой
результирующей силы F .
По второму закону Ньютона:
p2
t2
p1
t1
dp Fdt
F
dp
,
dt
dp Fdt
t2
p2 p1 p Fdt
t1
p1
импульс материальной точки в момент времени t1.
p2
импульс материальной точки в момент времени t2.
импульс
силы
Изменение импульса материальной точки p равно импульсу
результирующей силы, действующему на материальную точку за
промежуток времени t t2 t1 .
1-й закон
Импульс материальной точки сохраняется,
если результирующая сила равна 0.
Ньютона

40.

Третий закон Ньютона,
закон изменения и сохранения импульса
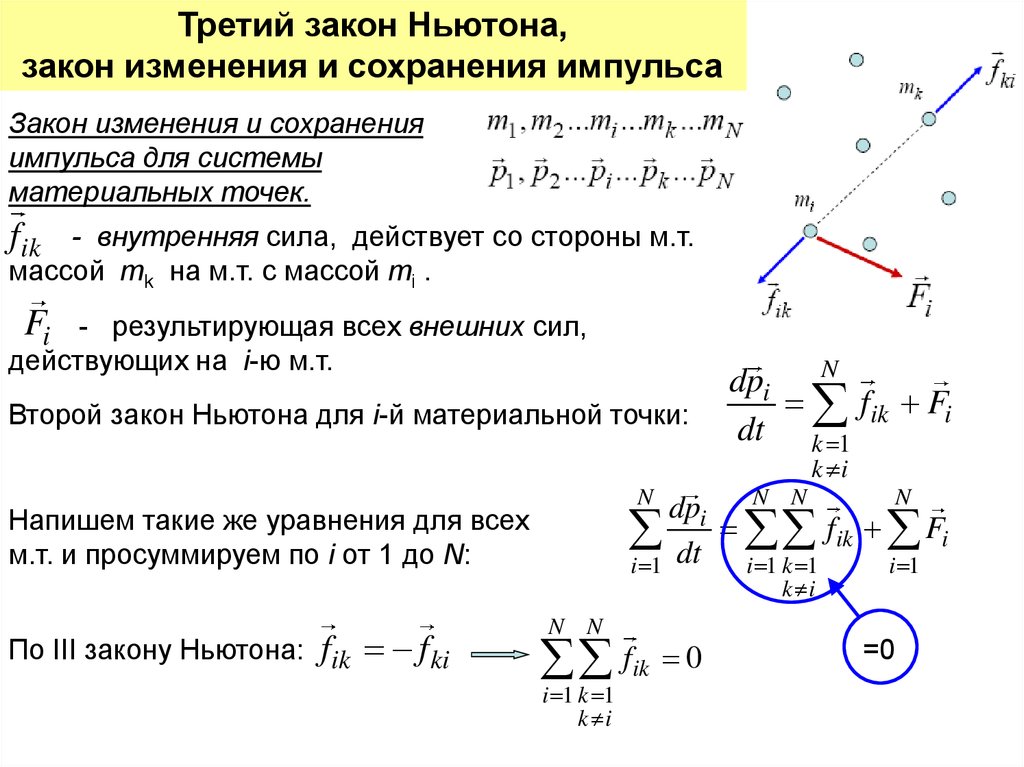
Закон изменения и сохранения
импульса для системы
материальных точек.
- внутренняя сила, действует со стороны м.т.
массой mk на м.т. с массой mi .
f ik
Fi
- результирующая всех внешних сил,
действующих на i-ю м.т.
Второй закон Ньютона для i-й материальной точки:
dpi N
fik Fi
dt k 1
k i
N
N
dpi N N
dt fik Fi
i 1
i 1 k 1
i 1
Напишем такие же уравнения для всех
м.т. и просуммируем по i от 1 до N:
k i
По III закону Ньютона: fik
f ki
N N
fik 0
i 1 k 1
k i
=0

41.

Третий закон Ньютона,
закон изменения и сохранения импульса
Закон изменения и сохранения импульса для
системы материальных точек.
=
dP
F.
dt
dP Fdt
Скорость изменения импульса системы м.т. (тел) равна
результирующей всех внешних сил.
dP
t2
p1
t1
P2
Fdt
t2
P2 P1 P Fdt
t1

42.

Третий закон Ньютона, закон изменения и сохранения импульса
Закон изменения и сохранения импульса для
системы материальных точек.
P2 P1 P Fdt
Закон изменения импульса:
Изменение импульса системы материальных точек за
некоторый промежуток времени равно импульсу
результирующей всех внешних сил, действующих на
систему за этот промежуток времени.
F 0
P const
Импульс системы материальных точек есть величина
постоянная, если векторная сумма всех внешних сил,
действующих на систему, равна нулю.
Частный случай: P const
в
замкнутой (изолированной) системе.
Пример: реактивное движение.
t2
t1
Пример

43.

Третий закон Ньютона,
закон изменения и сохранения импульса
Закон сохранения импульса в замкнутой системе – фундаментальный
закон физики.
Закон сохранения импульса в замкнутой системе - справедлив не только в
классической, но и в релятивистской и квантовой механике.
Закон сохранения импульса в замкнутой системе можно вывести из
однородности пространства, не прибегая к 3 закону Ньютона.
Тогда 3 закон Ньютона получится как следствие закона сохранения
импульса или следствие однородности пространства.

44.

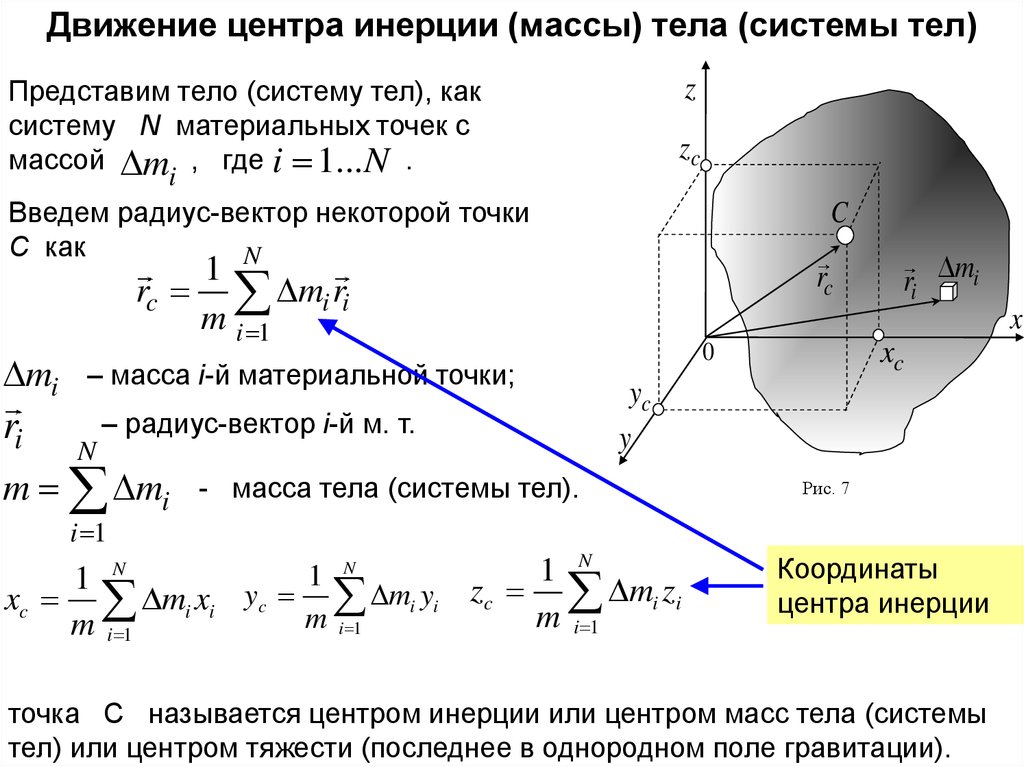
Движение центра инерции (массы) тела (системы тел)
Представим тело (систему тел), как
систему N материальных точек с
массой m , где i 1...N .
z
zc
i
Введем радиус-вектор некоторой точки
C как
N
C
1
rc mi ri
m i 1
mi
ri
ri mi
x
– масса i-й материальной точки;
– радиус-вектор i-й м. т.
N
m mi
rc
xc
0
yc
y
- масса тела (системы тел).
Рис. 7
i 1
N
1
xc mi xi
m i 1
1 N
yc mi yi
m i 1
1 N
zc mi zi
m i 1
Координаты
центра инерции
точка С называется центром инерции или центром масс тела (системы
тел) или центром тяжести (последнее в однородном поле гравитации).

45.

Движение центра инерции (массы)
тела (системы тел)
z
zc
C
1 N
rc mi ri
m i 1
Скорость центра инерции
ri mi
rc
x
xc
0
yc
y
drc 1 N
dri
1 N
1 N
1
mi vi pi P
vc
mi
m i 1
m i 1
m
dt m i 1
dt
Рис. 7
P mvc
Полный импульс системы материальных точек (тела) равен
произведению массы системы материальных точек (тела) на скорость
центра инерции.
dP d (mvc )
Для изменения полного импульса системы найдено
F
dt
dt
Центр инерции тела (системы тел) движется так же, как двигалась бы
материальная точка с массой m под действием результирующей
всех внешних сил, приложенных к телу (системе тел).

46.

Пример:
Топор совершает сложное движение.
Однако в соответствии с теоремой о
движении центра масс, его ц.м. движется так
как двигалась бы материальная точка в поле
силы тяжести, если она имела начальную
скорость направленную под углом к
горизонту.
Это важная информация о движении
топора, хотя и неполная.
Пример . В некоторой точке
траектории снаряд разрывается на
множество осколков. Как будет
двигаться их центр масс?
По той же траектории (парабола).
Сколь долго это продолжится?
Пока первый осколок не достигнет земли (добавится внешняя сила
реакции земли).

47.

Пример. На покоящееся тело начинает
действовать "пара" сил F и F*. Как будет
двигаться тело?
Геометрическая сумма внешних сил равна нулю
ускорение центра масс также равно нулю - он останется
в покое.
Будет ли тело двигаться?
Оно будет вращаться вокруг оси проходящей через
неподвижный центр масс.
Центр тяжести.
В однородном поле тяготения равнодействующая сил тяжести приложена
к центру масс тела (системы тел).
Если тело подвешено за
центр масс, то оно находится в безразличном состоянии равновесия.