Обработка данных. Задачи локального и глобального интерполирования

1. Практический семинар по Математической экономике (17.М18-э + 17.М19-э)

Занятие 2
ОБРАБОТКА ДАННЫХ.
Задачи локального и глобального
интерполирования.
2018/2019 уч. год
01.11.2018
Занятие 1
1

2. Задача локального интерполирования. Пример

Пусть известны значения функции y = f (x) в 5 узлах
(т.е. дана интерполяционная задача с 5 узлами):
x
y
0
1
2
3
4
1 .0 1 . 8 2 . 2 1 .4 1 . 0
Требуется найти полиномы 1-й и 2-й степени, удовлетворяющие
условию интерполирования в окрестности точки x*=2.3:
P1 :
P2 :
01.11.2018
P1( 2) 2.2
P1( 3) 1.4
P 2(1) 1.8
P 2( 2) 2.2
P 2( 3) 1.4
Интерполяционная задача
2

3. Постановка задачи. Условие интерполирования

Пусть дана интерполяционная
задача
с
n узлами:
x
x
x
x1 1,xx2 2 , x…3 ,...,xxn n , x x , i, j 1, 2,.., n
i
j
y
y
,
y
,
y
,...,
y
1
2
3
n
y
y1
y2
…
yn
Найти полином степени не выше чем (n-1),
удовлетворяющий условию
интерполирования:
y f x a 0 a1x a 2 x 2 a 3 x 3 ... a n 1x n 1 : f x i y i
y1 f x1 a 0 a1x1 a 2 x12 ... a n 1x1n 1,
y 2 f x 2 a 0 a1x 2 a 2 x 22 ... a n 1x n2 1,
...........................................................................
y n f x n a 0 a1x n a 2 x 2n ... a n 1x nn 1.
01.11.2018
Интерполяционная задача
3

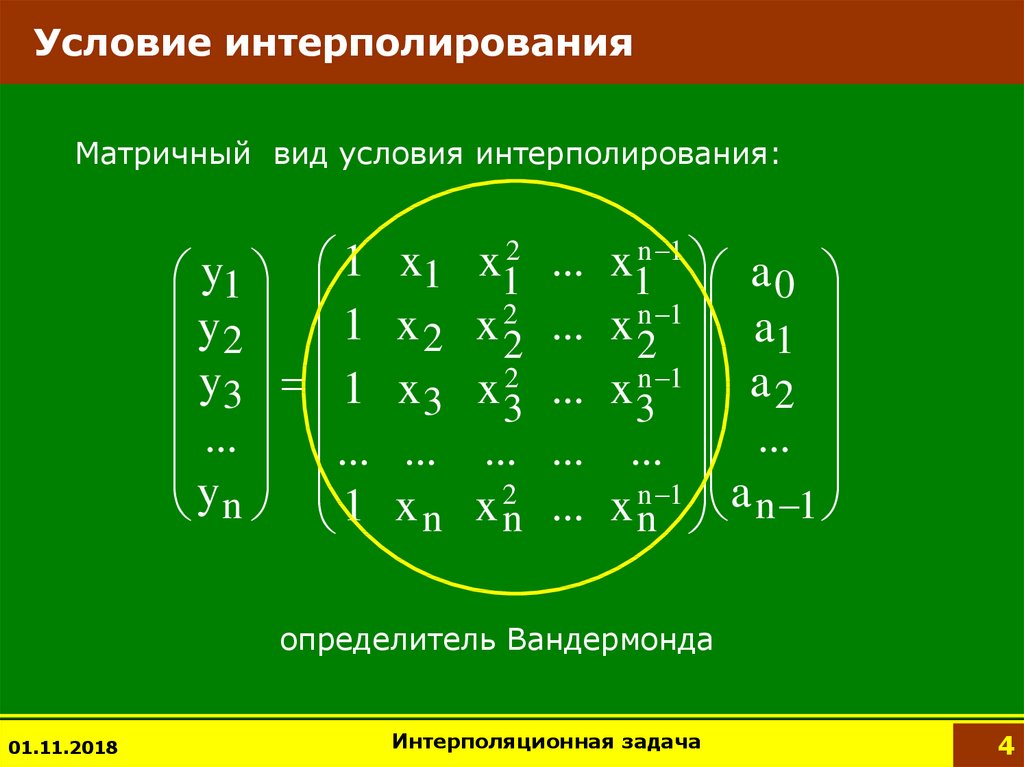
4. Условие интерполирования

Матричный вид условия интерполирования:
y1 1
y
1
2
y3 1
... ...
y
n 1
x1
x2
x3
...
xn
x12
x 22
x 32
...
x n2
...
...
...
...
...
x1n 1 a 0
n 1
x 2 a1
x 3n 1 a 2
...
...
n 1 a
x n n 1
определитель Вандермонда
01.11.2018
Интерполяционная задача
4

5. Пример решения задачи локального интерполирования

x
y
0
1
2
3
4
1 .0 1 . 8 2 . 2 1 .4 1 . 0
a 0 a1 2 2,2
a 0 a1 3 1,4
a 0 3,8; a1 0,8
P1 3,8 0,8x
a 0 a1 1 a 2 12 1,8
2 2,2
a
a
2
a
2
0 1
2
2 1,4
a
a
3
a
3
0 1
2
01.11.2018
в окрестности точки
x*=2,3
a 0 0,2; a1 2,2; a 2 0,6;
P 2 0,2 2,2 x 0,6 x 2
Интерполяционная задача
5

6. Пример 1

Построить интерполяционный полином по таблице
01.11.2018
x
0
2
3
f(x)
1
3
2
Квадратичные формы
6

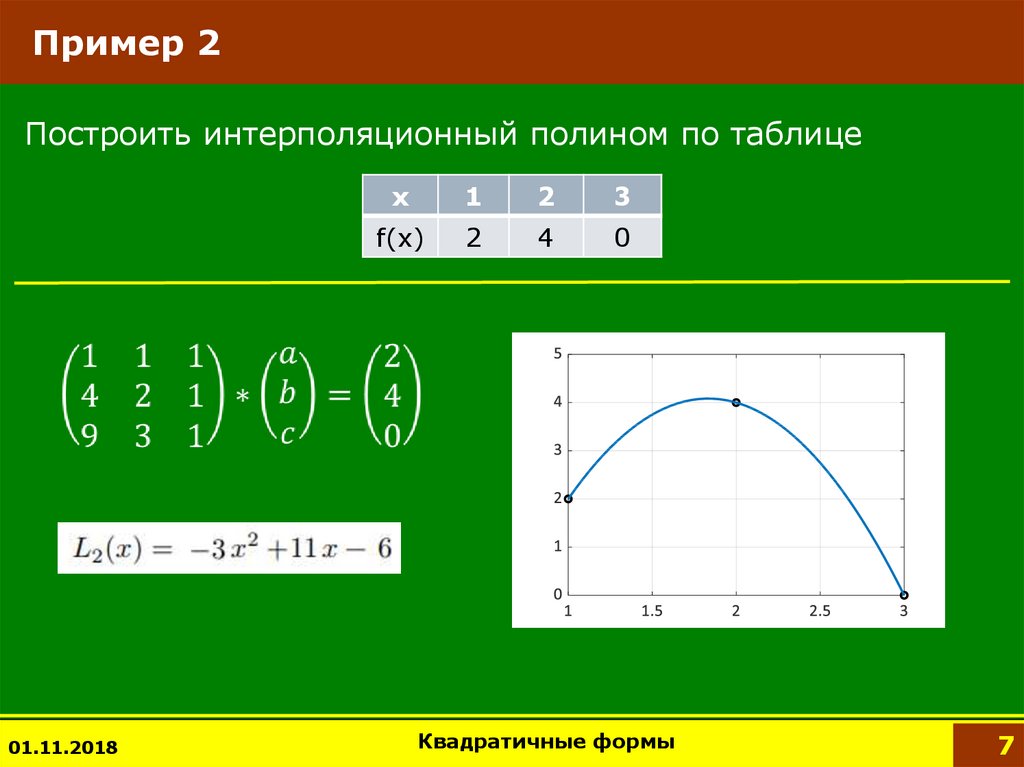
7. Пример 2

Построить интерполяционный полином по таблице
01.11.2018
x
1
2
3
f(x)
2
4
0
Квадратичные формы
7

8. Замечание о применимости подхода

01.11.2018
Квадратичные формы
8

9. Полином Лагранжа

В частности,
01.11.2018
Квадратичные формы
9

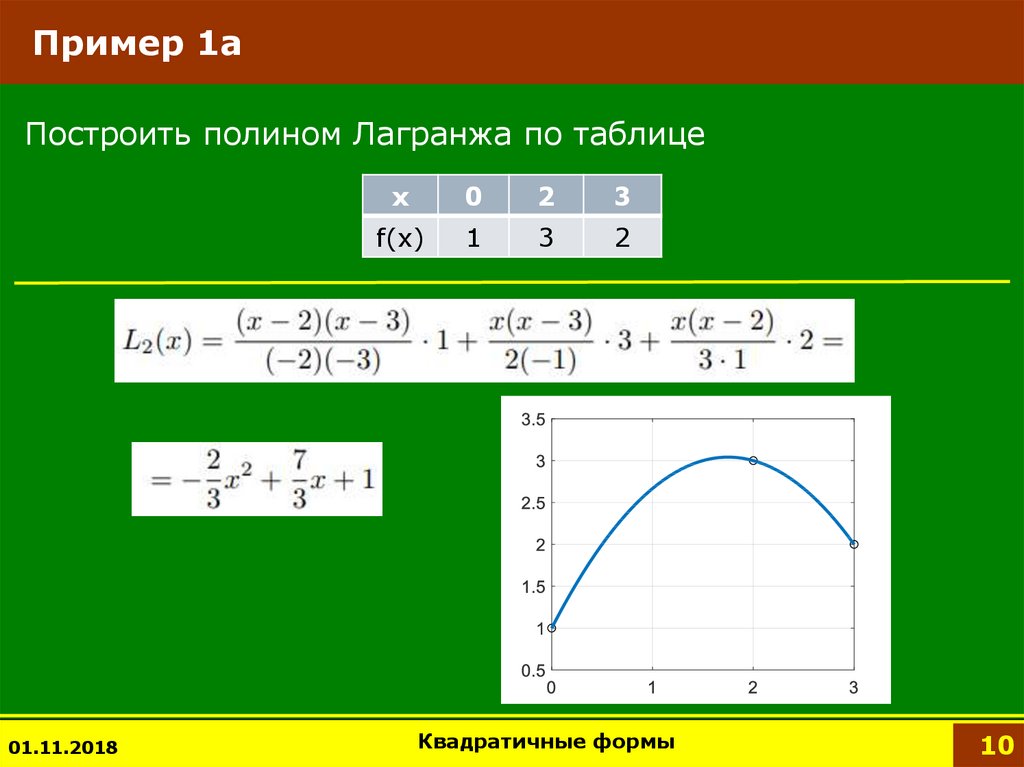
10. Пример 1а

Построить полином Лагранжа по таблице
01.11.2018
x
0
2
3
f(x)
1
3
2
Квадратичные формы
10

11. Пример 2а

Построить полином Лагранжа по таблице
01.11.2018
x
1
2
3
f(x)
2
4
0
Квадратичные формы
11

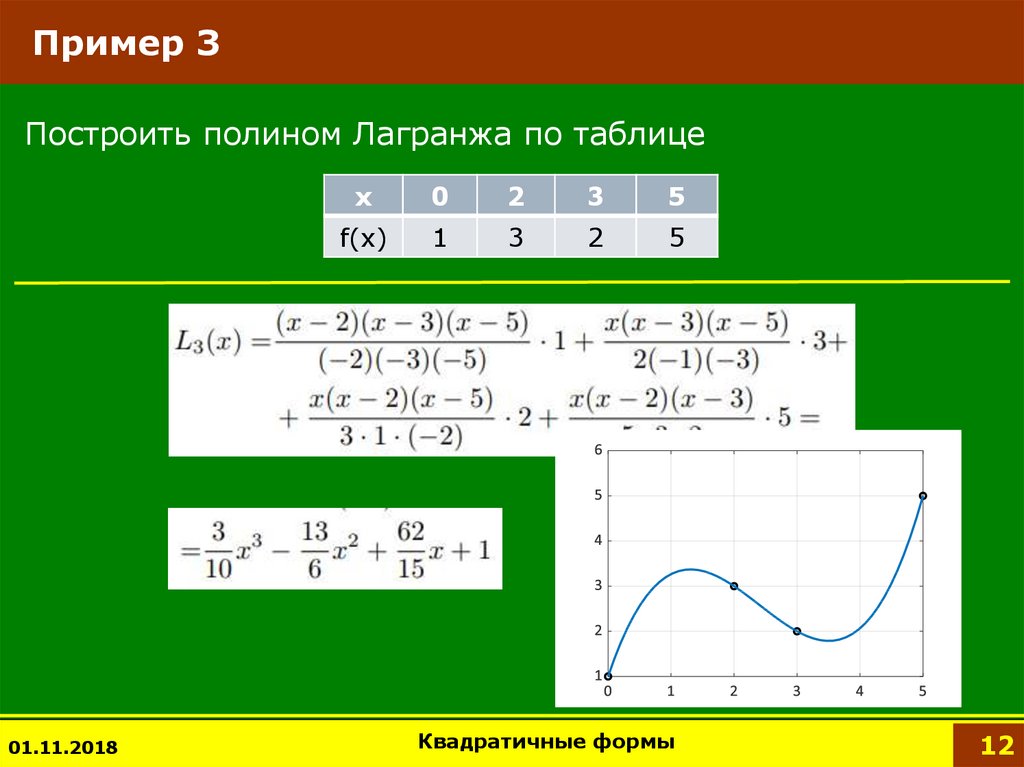
12. Пример 3

Построить полином Лагранжа по таблице
01.11.2018
x
0
2
3
5
f(x)
1
3
2
5
Квадратичные формы
12

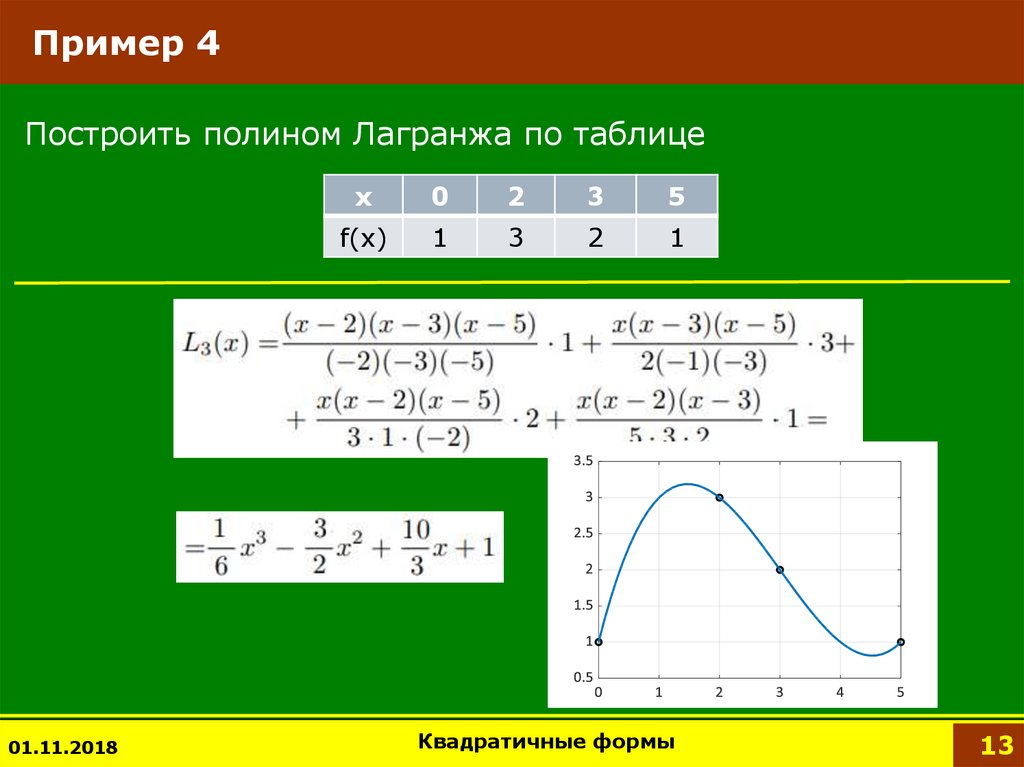
13. Пример 4

Построить полином Лагранжа по таблице
01.11.2018
x
0
2
3
5
f(x)
1
3
2
1
Квадратичные формы
13

14. Интерполяционный кубический сплайн (ИКС)

Определение
Пусть {xi } - интерполяционная сетка на отрезке [a,b] и
(xi,yi) - точки данных. Интерполяционным кубическим
сплайном называется функция S(x) , обладающая
следующими свойствами:
1. Функция S(x) непрерывна на отрезке [a,b] вместе cо
своими производными S’(x) и S’’(x);
2. На каждом частичном отрезке [xk-1, xk] S(x) совпадает с
некоторым алгебраическим многочленом третьей степени
P3,k(x)=a0+a1(x-xk-1)+a2(x-xk-1)2+a3(x-xk-1)3
3. S(x) удовлетворяет условию интерполирования
S(xi ) = yi , i=1, 2,…,n
01.11.2018
Интерполирование сплайнами
14

15. Две формы записи ИКС

01.11.2018
Интерполирование сплайнами
15

16. Идея алгоритма построения ИКС

01.11.2018
Интерполирование сплайнами
16

17. Идея алгоритма построения ИКС

k=1,2,…,N-1
01.11.2018
Интерполирование сплайнами
17

18. Граничные условия «естественный сплайн»

01.11.2018
Интерполирование сплайнами
18

19. Граничные условия «отсутствие узла»

01.11.2018
Интерполирование сплайнами
19

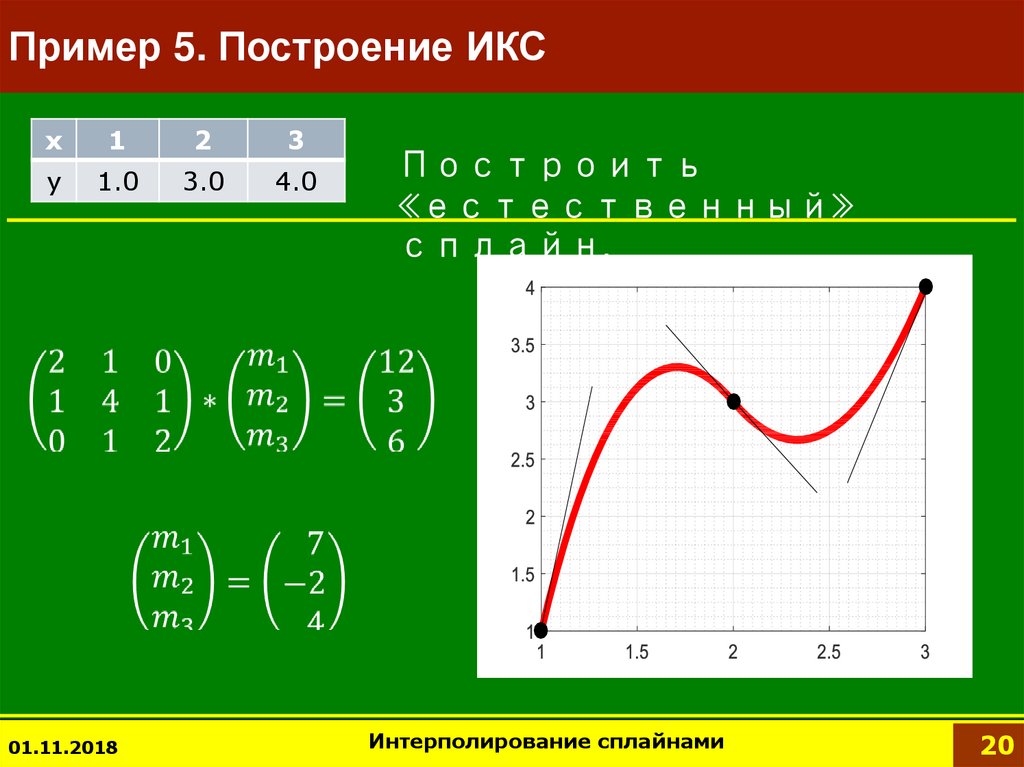
20.

Пример 5. Построение ИКС
x
1
2
3
y
1.0
3.0
4.0
01.11.2018
Построить
«естественный»
сплайн.
Интерполирование сплайнами
20

21.

Пример 6. Построение ИКС
x
1
2
3
y
1.0
3.0
5.0
01.11.2018
Построить сплайн с
условием
«отсутствие узла».
Интерполирование сплайнами
21

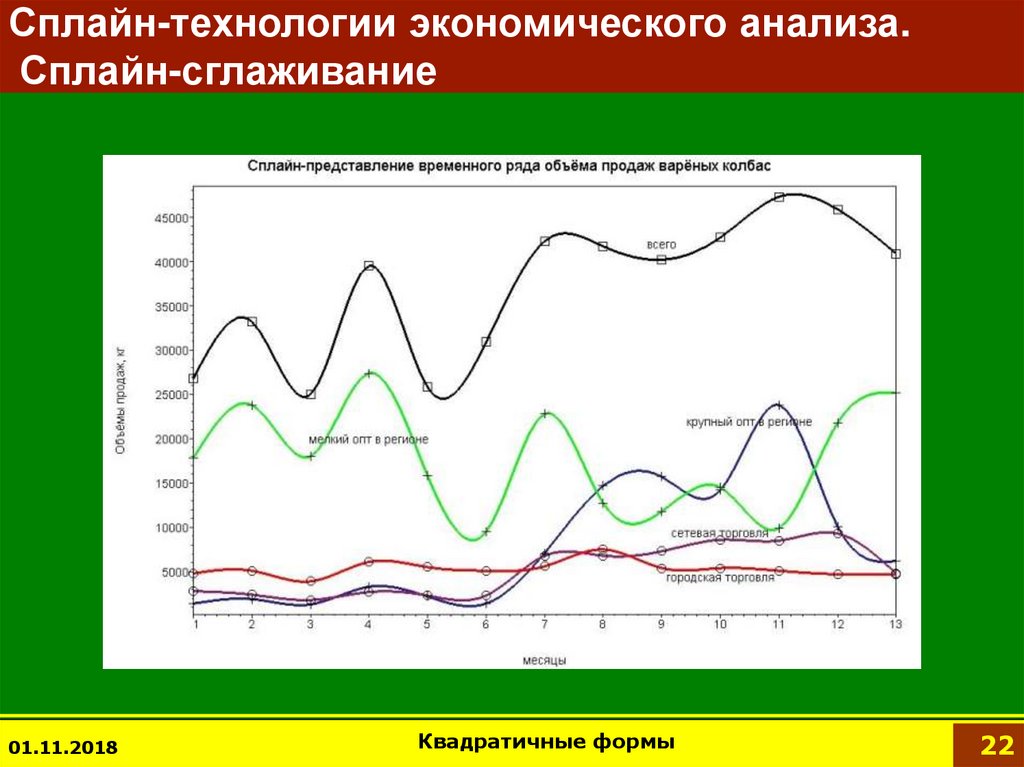
22.

Сплайн-технологии экономического анализа.
Сплайн-сглаживание
01.11.2018
Квадратичные формы
22

23.

Сплайн-технологии экономического анализа.
Фазовый портрет динамики продаж
01.11.2018
Квадратичные формы
23