Похожие презентации:
Поверхности
1. Поверхности
доцент кафедрыИнженерная графика и дизайн
НИТУ «МИСиС»
Дербенева О.Л. olderbeneva@mail.ru
2015 г.
1
2.
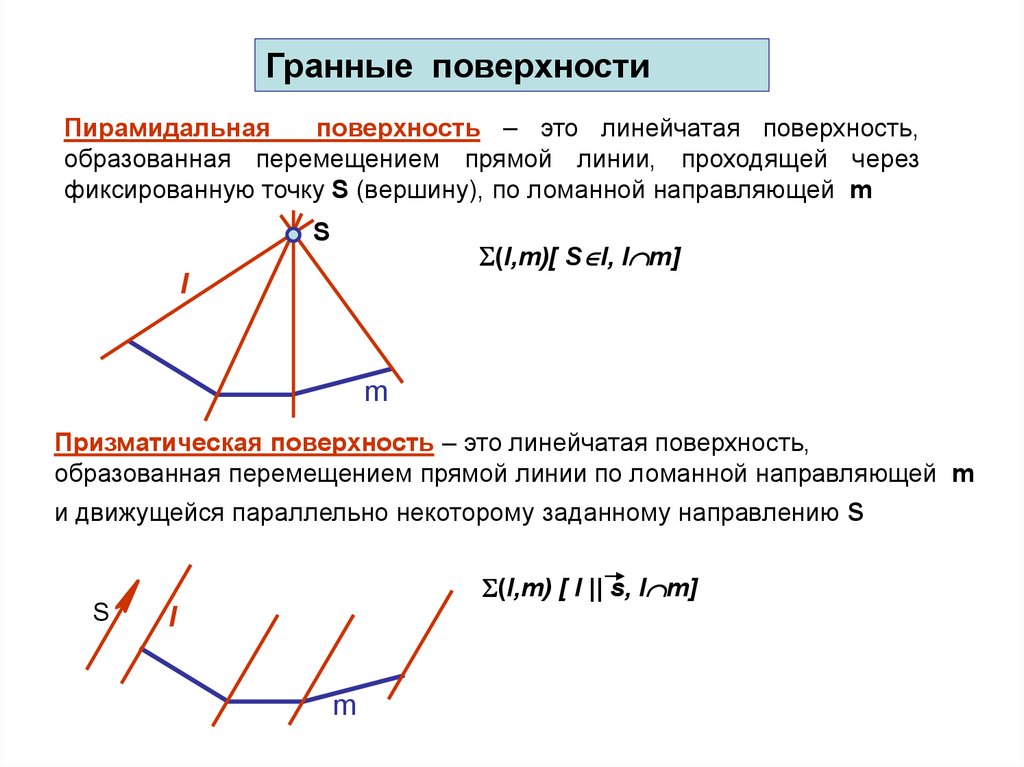
Гранные поверхностиПирамидальная
поверхность – это линейчатая поверхность,
образованная перемещением прямой линии, проходящей через
фиксированную точку S (вершину), по ломанной направляющей m
S
(l,m)[ S l, l m]
l
m
Призматическая поверхность – это линейчатая поверхность,
образованная перемещением прямой линии по ломанной направляющей m
и движущейся параллельно некоторому заданному направлению s
S
(l,m) [ l || s, l m]
l
m
3.
Гранные поверхностиМногогранником называют замкнутые пространственные
фигуры, ограниченные плоскими многоугольниками.
Грани - многоугольники многогранника.
Ребра – линии пересечения граней.
Вершины – точки пересечения ребер.
S2
M2
N2 N21
А2
В2
12
N11 111
А1
S1
В1
N1
С2
С1
А2
С2
В2
А1
С1
11
M1
В1
4.
Линейчатые поверхностивращения
Коническая поверхность –поверхность, образованная вращением прямолинейной
образующей вокруг пересекающейся с ней оси.
ось
Σ ( l, i) [ l i] – коническая поверхность
Образующая
12
22
11
21
5.
Линейчатые поверхностиось
вращения
Σ ( l, i) [ l i] – коническая поверхность
Образующая
32
31
6.
Линейчатые поверхностиось
вращения
Σ ( l, i) [ l i] – коническая поверхность
Образующая
42
41
7.
Линейчатые поверхностивращения
Цилиндрическая поверхность –поверхность, образованная вращением
прямолинейной образующей вокруг оси.
Г ( l, i)[ l ||i ]– цилиндрическая поверхность
ось
Образующая
12
11
8.
Поверхности вращениягорло
образующая
R
параллели
экватор
Параллель -это окружность, с центром на оси вращения, которую
описывает каждая точка образующей при вращении вокруг оси
Радиус параллели равен расстоянию от оси до очерка
Параллель наименьшего диаметра называется горлом
Параллель наибольшего диаметра называется экватором
9.
Поверхности вращенияМеридиональная плоскость
меридиан
Плоскость, проходящая через ось поверхности вращения
называется меридиональной плоскостью
Линия пересечения меридиональной плоскости с поверхностью
вращения называется меридианом
10.
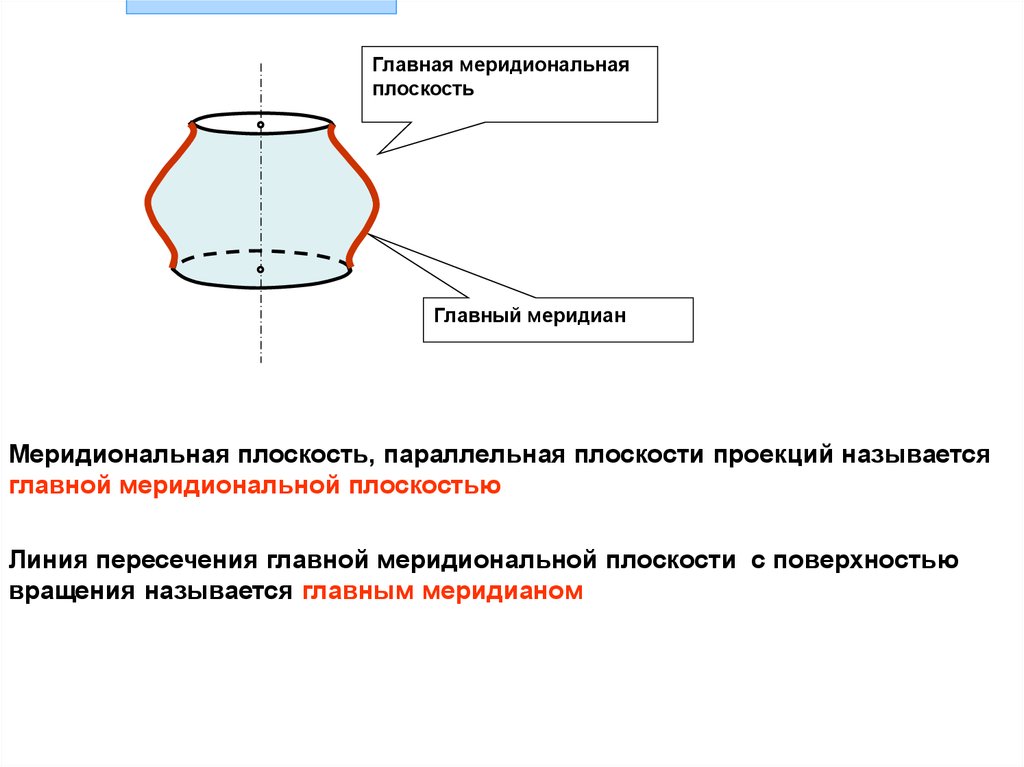
Главная меридиональнаяплоскость
Главный меридиан
Меридиональная плоскость, параллельная плоскости проекций называется
главной меридиональной плоскостью
Линия пересечения главной меридиональной плоскости с поверхностью
вращения называется главным меридианом
11.
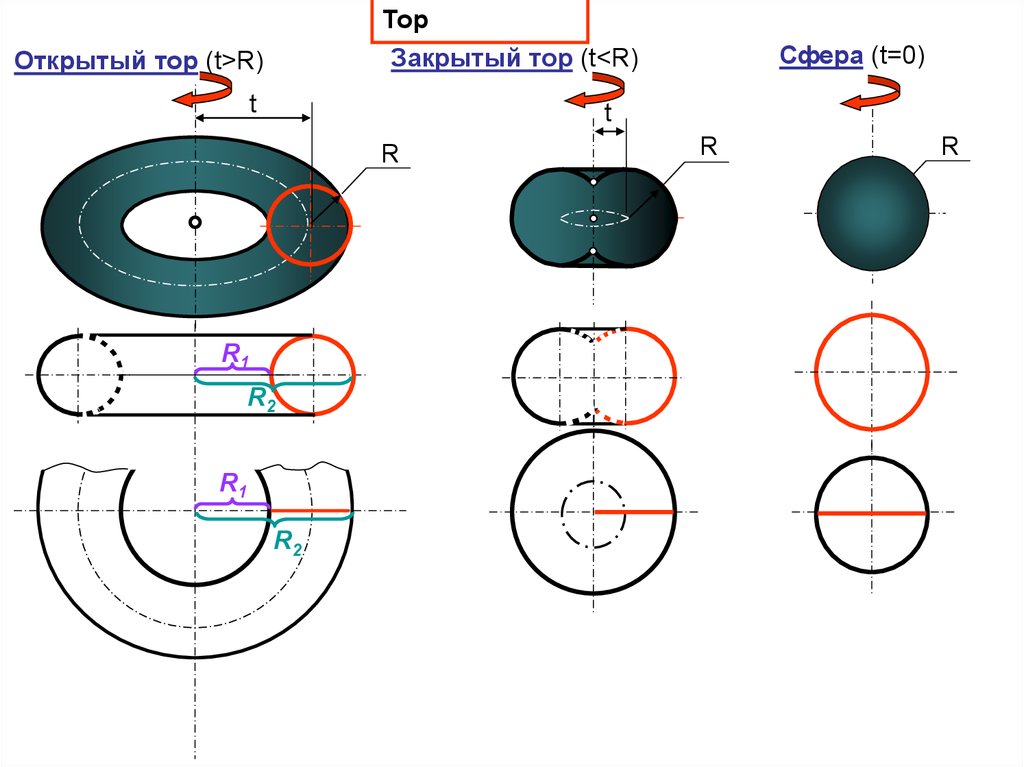
ТорЗакрытый тор (t<R)
Открытый тор (t>R)
t
Сфера (t=0)
t
R
R1
R2
R1
R2
R
R
12.
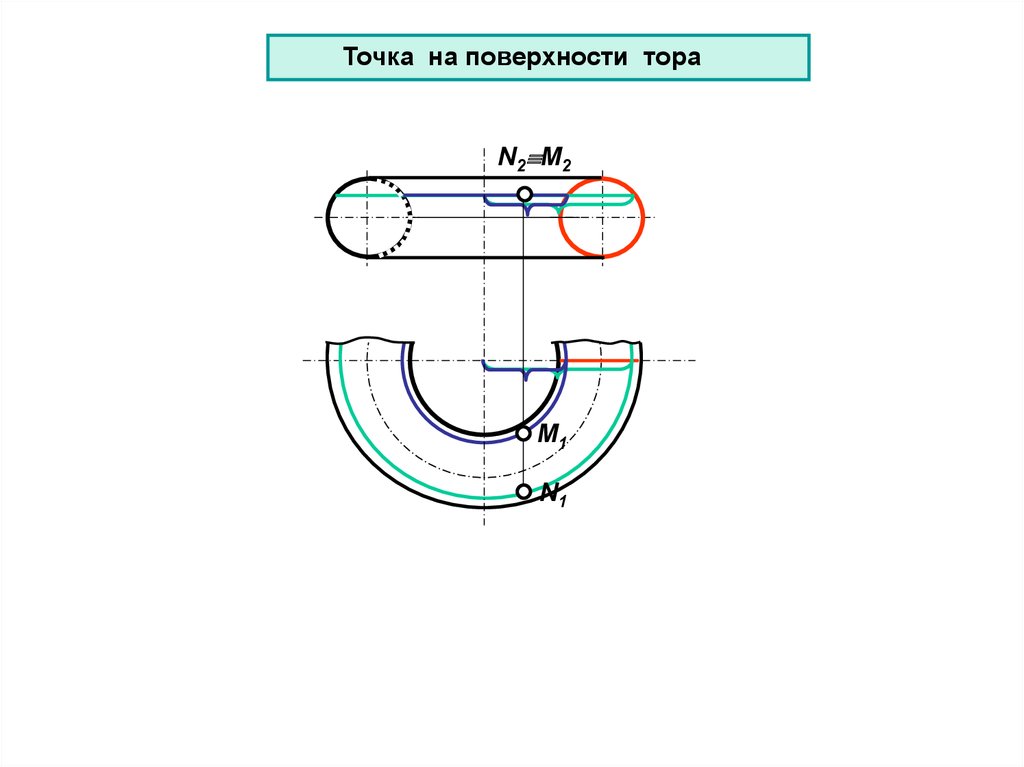
Точка на поверхности тораN2 M2
N11
M11
M1
N1
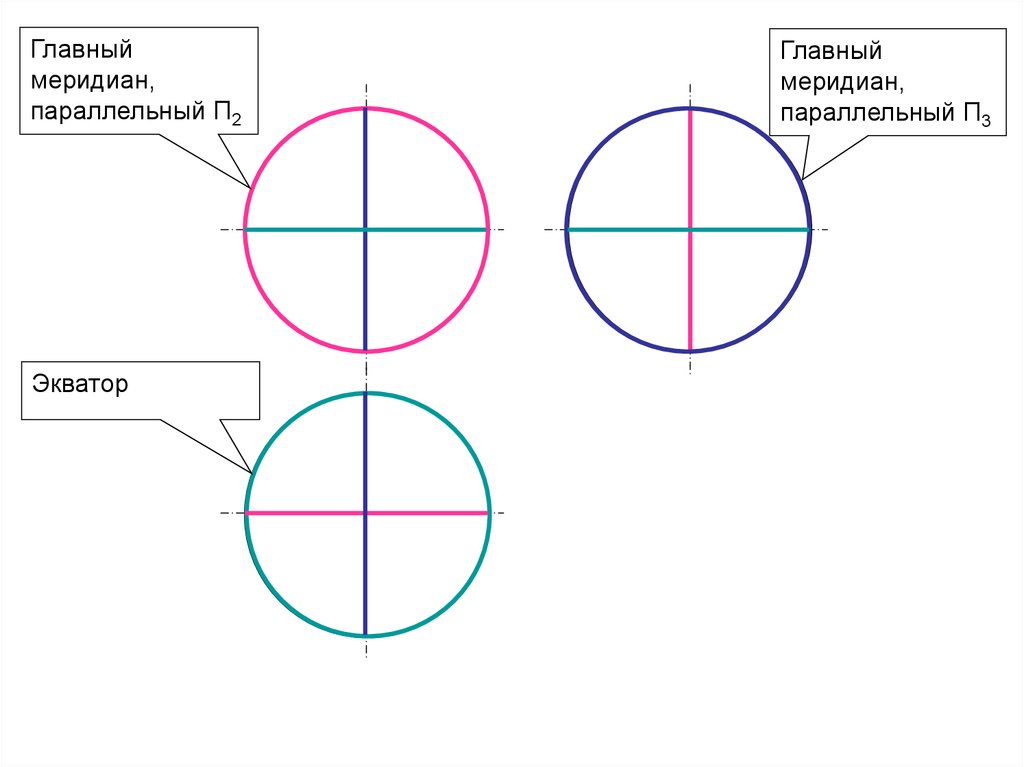
13.
Точка на поверхности сферыГлавный меридиан,
параллельный П2
Экватор
14.
Точка на поверхности сферыпараллель
А2 А21
Радиус
параллели
А11
А1
15.
В2В21
В1 В11
Радиус
окружности
В3
В31
16.
Радиусокружности
М2
М1
М 21
М11
М3 М 31
17.
Главныймеридиан,
параллельный П2
Экватор
Главный
меридиан,
параллельный П3
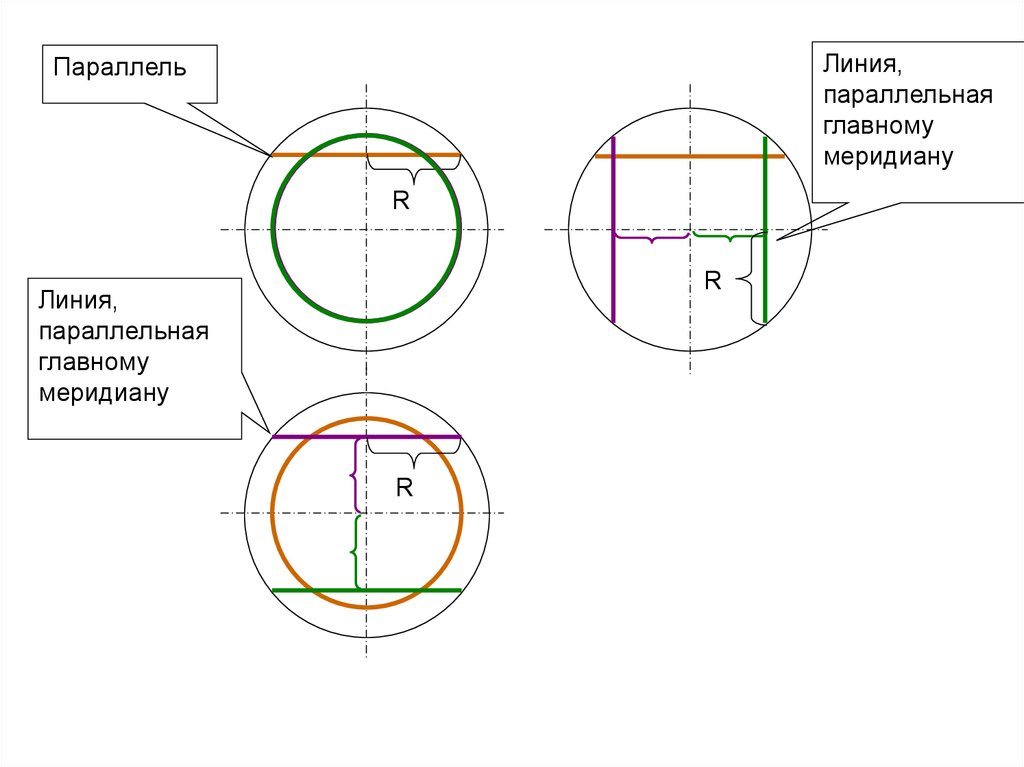
18.
Линия,параллельная
главному
меридиану
Параллель
R
R
Линия,
параллельная
главному
меридиану
R
19.
Главный меридиан,параллельный П2
А2
А1
А3
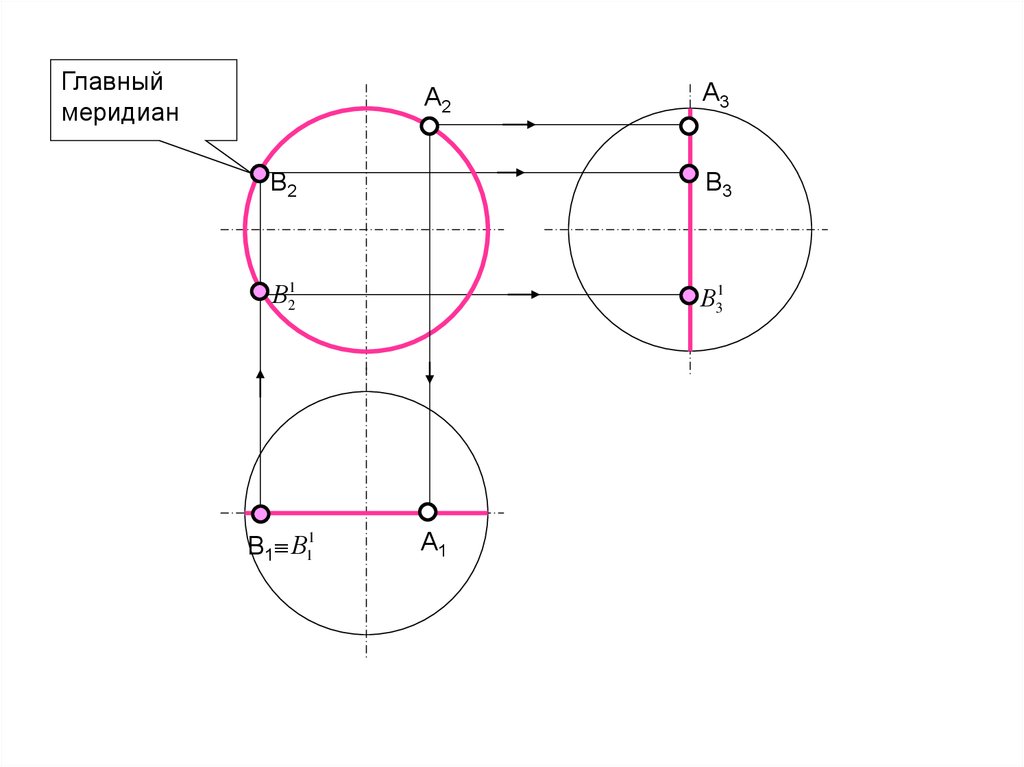
20.
Главныймеридиан
А2
А3
В2
В3
В21
В31
В1 В11
А1
21.
Главныймеридиан
C2
C1
С21
С11
C3 С31
22.
ЭкваторD2 D21
D11
D1
D31
D3
23.
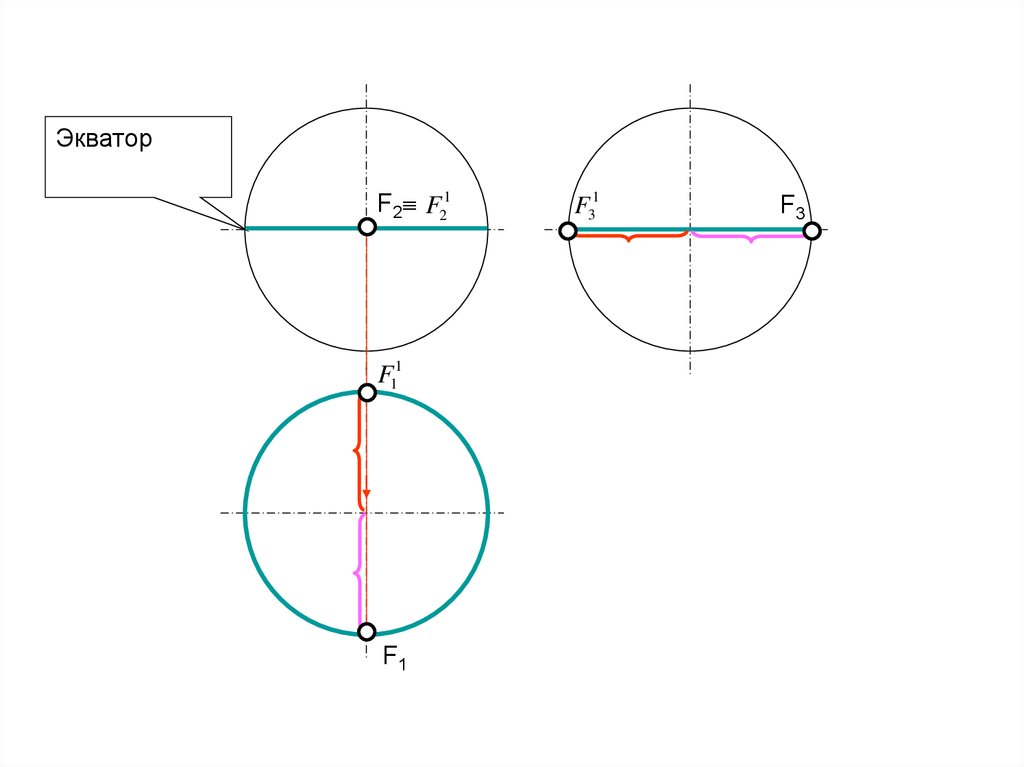
ЭкваторF2 F21
F11
F1
F31
F3
24.
ЭкваторК2
К1
K 21
K11
К3 К 31
25.
Главный меридиан,параллельный П3
М2
М1
М3
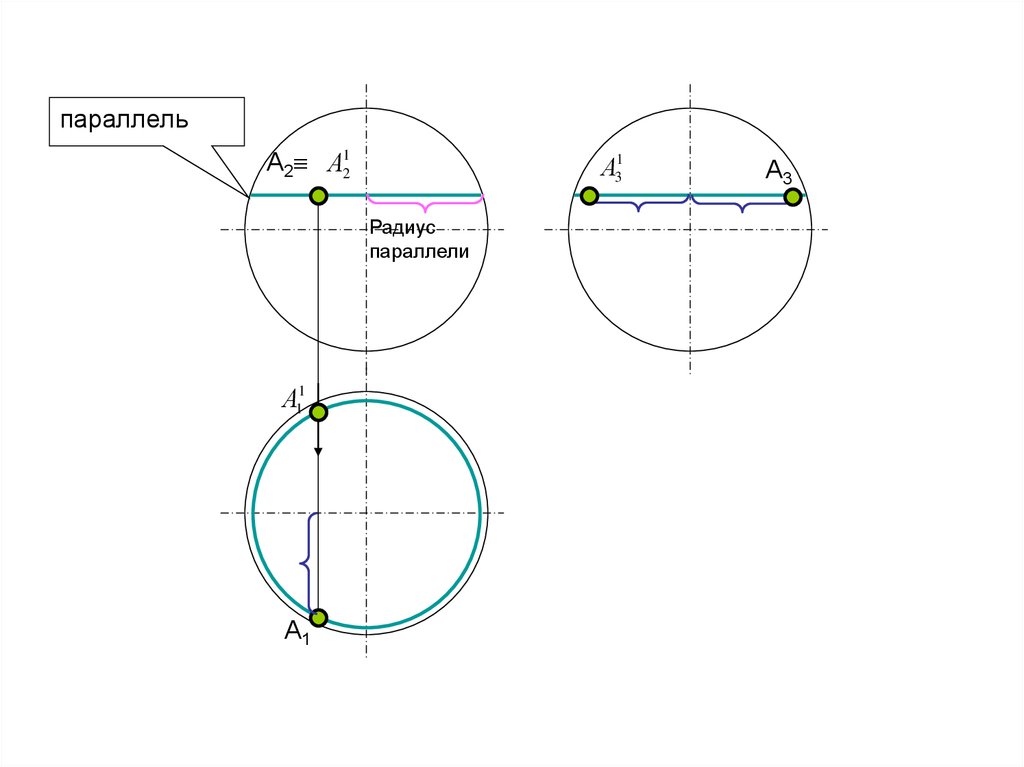
26.
параллельА2 А21
А31
Радиус
параллели
А11
А1
А3
27.
Главныймеридиан,
параллельный П2
Экватор
Главный
меридиан,
параллельный П3
28.
Линия,параллельная
главному
меридиану
Параллель
R
R
Линия,
параллельная
главному
меридиану
R
29.
Главный меридиан,параллельный П2
А2
А1
А3
30.
Главныймеридиан
А2
А3
В2
В3
В21
В31
В1 В11
А1
31.
Главныймеридиан
C2
C1
С21
С11
C3 С31
32.
ЭкваторD2 D21
D11
D1
D31
D3
33.
ЭкваторF2 F21
F11
F1
F31
F3
34.
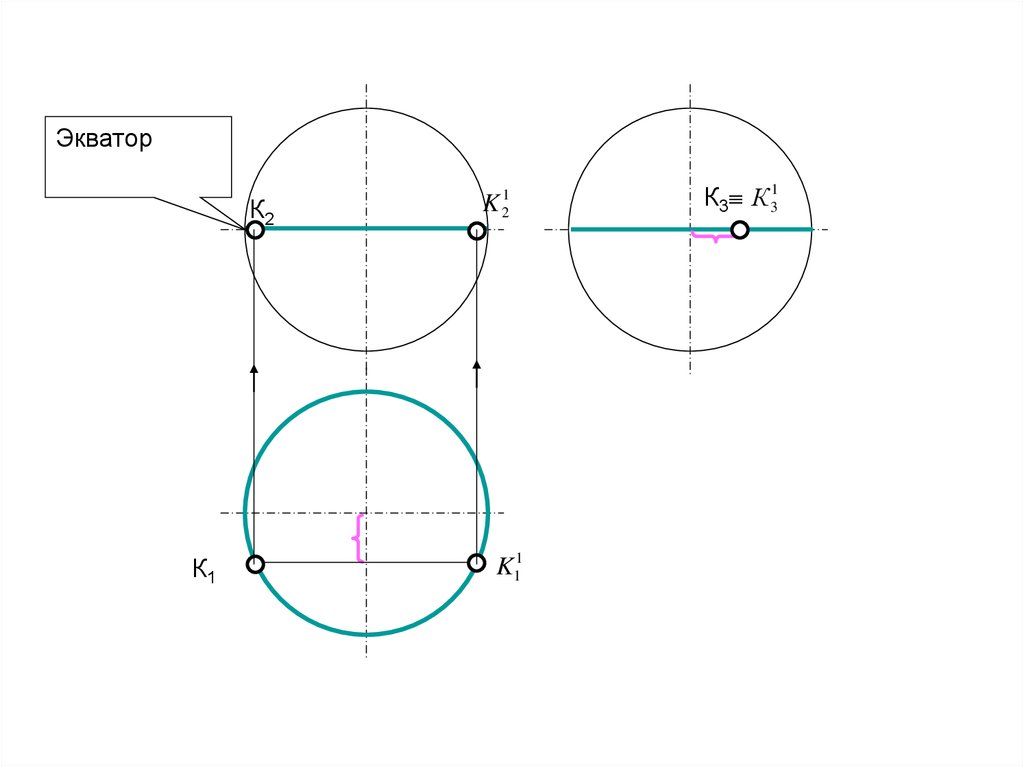
ЭкваторК2
К1
K 21
K11
К3 К 31
35.
Главный меридиан,параллельный П3
М2
М1
М3
36.
37.
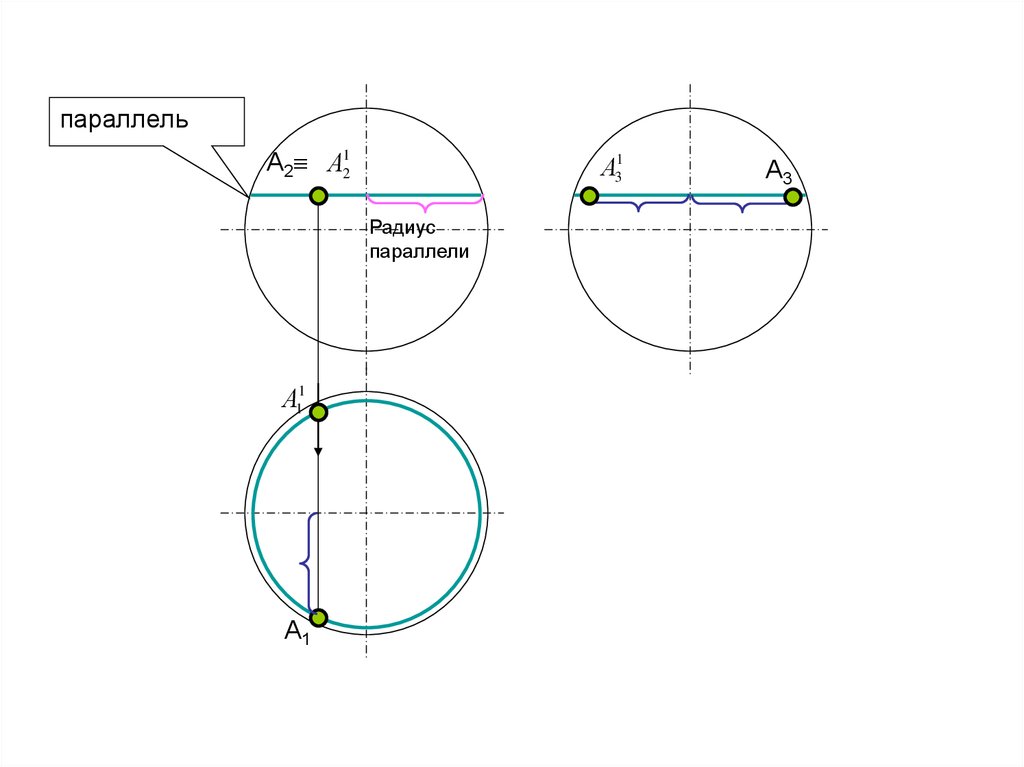
параллельА2 А21
А31
Радиус
параллели
А11
А1
А3
38.
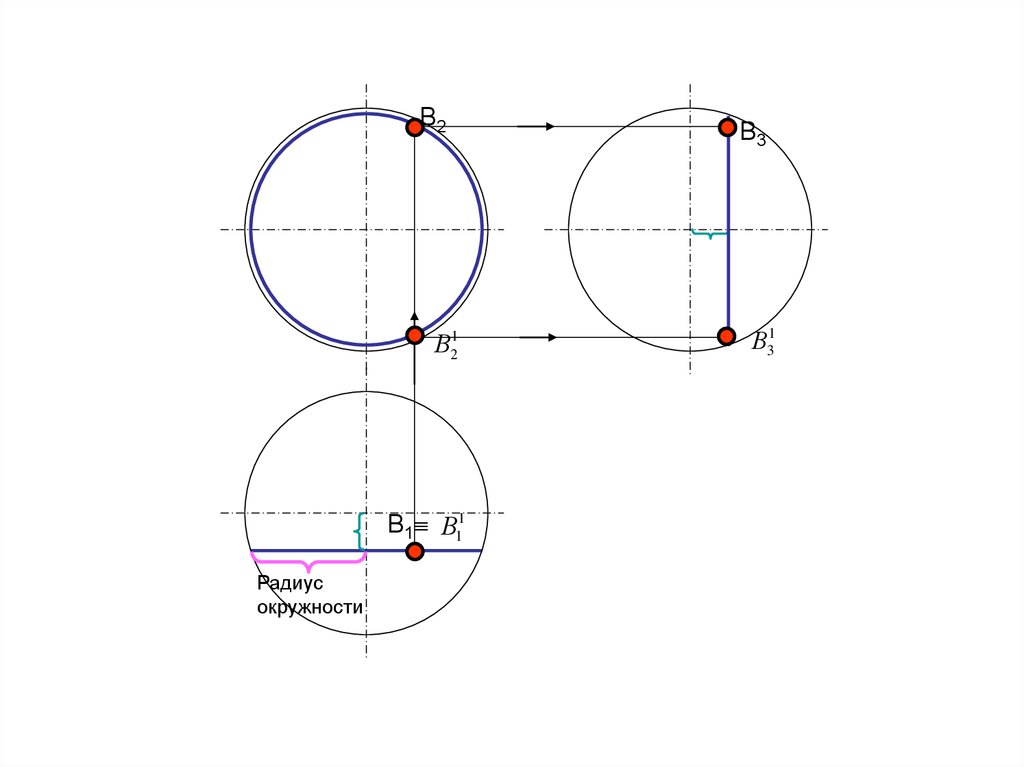
В2В21
В1 В11
Радиус
окружности
В3
В31
39.
Радиусокружности
М2
М1
М 21
М11
М3 М 31
40.
Промежуточнаяобразующая
Очерковая
образующая
41.
42.
Эллипсоид вращенияПараболоид вращения
Гиперболоид вращения






























 Инженерная графика
Инженерная графика








